基于改進序列凸優化的固體火箭入軌制導方法

王洪波，張若男，梁 卓，呂 瑞

（中國運載火箭技術研究院，北京 100076）

耗盡關機固體運載火箭的推力大小和工作時間無法主動控制，如何利用有限速度調節能力實現高精度入軌，是當前國內外固體火箭制導領域研究熱點。凸優化算法有確定收斂性、求解快速的優點，能夠滿足多飛行階段固體運載火箭的在線規劃和制導要求。

文獻[1][2]利用凸優化方法解決火箭上升動力段入軌制導問題，其發動機推力可調，末端關機時間可控；文獻[3]使用凸優化方法尋找火箭上升段推力下降故障時最優圓軌，但其只作為后續迭代初值，未嚴格考慮終端約束；文獻[4][5]針對運載器回收制導問題，構建多階段二階錐規劃模型，利用序列凸化算法離散求解；文獻[6]建立了有限推力遠程軌道轉移問題的凸優化模型，利用迭代逼近驗證凸優化算法在遠程軌跡規劃問題中的可行性。

基于此，本文研究耗盡關機固體火箭入軌制導問題，建立含推力方向和終端入軌參數約束的“滑行段+動力段”運動模型。使用拉道（Legendre–Gauss–Radau，LGR）偽譜法離散滑行段運動模型，將點火時間增廣為新的控制變量；將推力方向非凸球面可行域松弛為凸球體可行域。并從理論上證明松弛的無損性，同時對運動方程和終端等式約束進行線性化，構建凸優化子問題；利用含初值生成器的序列凸優化算法迭代逼近原問題，得到最優滑行時間和最優推力矢量，實現耗盡關機固體火箭動力段能量管理，最終高精度入軌。

1 固體火箭多階段入軌制導模型

1.1 最優控制問題描述

本文所研究的固體子火箭入軌制導問題，飛行高度大于100 km，處于大氣層外，不考慮氣動影響[7]。動力段發動機推力為常值，火箭推力方向與箭體縱軸重合，姿態控制視作理想環節；飛行采用“滑行+動力”方案，在地心慣性系下建立的三自由度運動模型：

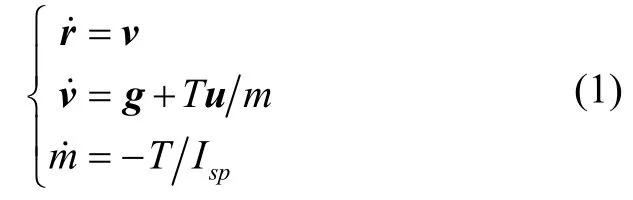
式中，狀態量r、v、m分別為坐標系下位置、速度和質量；g為火箭重力加速度：

Isp為發動機比沖；T為發動機推力，滑行段發動機推力為零，動力段發動機推力為不可調常值[8]，u為推力方向單位矢量：

設滑行段開始時間為t0=0，滑行段結束（動力段開始）時間為ts，終端時間為tf。

目標軌道為圓軌道，發動機燃料耗盡關機時，火箭需滿足目標軌道約束：

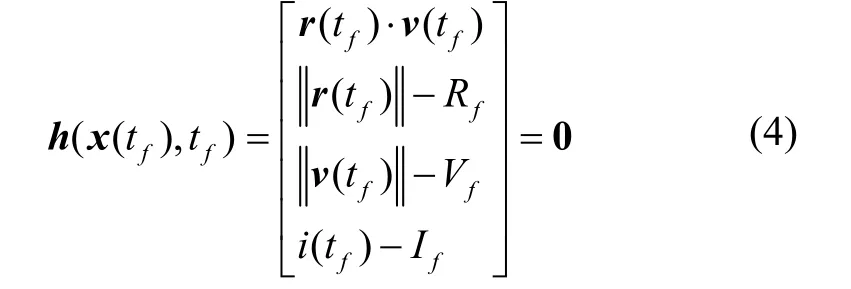
其中，Rf、Vf、If分別為目標軌道地心距、軌道速度和軌道傾角。

實際飛行中，長時間滑行中姿態調整將給姿控系統帶來不利影響，因此選擇飛行時間作為需要優化的性能指標：

綜上，固體火箭入軌段最優控制問題為式(1)-(5)。

該入軌制導問題分為滑行與動力兩階段，各段內狀態與控制量變化連續。由于滑行段時間較長，為了獲得較高的離散精度，采用收斂速度較快的LGR 偽譜法離散[9]；動力段時間相對較短，采用一階保持器的等距離散。

1.2 滑行段離散建模

LGR 偽譜法配點定義在[-1，+1)之間，將原問題時域映射至[-1，+1)區間內，如式(6):

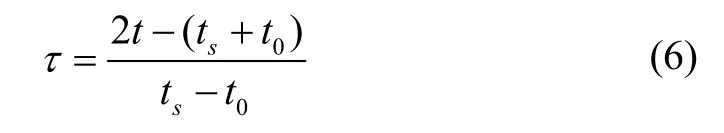
式中，τi(i=1...N1)是[-1，+1)上的N1階Legendre多項式零點。τs=+1 和τi(i=1...N1)構成N1+1個插值點。

為表述方便，以τ為變量的狀態量與控制量仍舊使用x、u表示，狀態量及其導數的插值近似為：

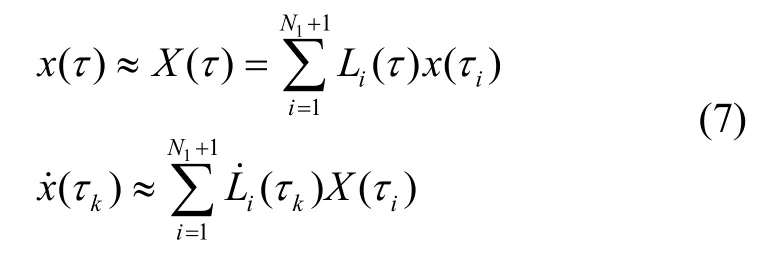
式中Li(i=1...N1+1)為Lagrange 插值基函數。

滑行段動力學方程離散模型如下：

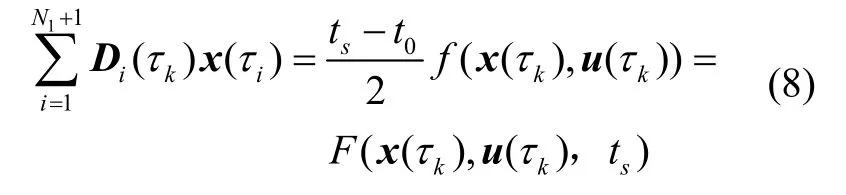
式中，D為N1×(N1+1)階微分矩陣，f(x(τk),u(τk))為動力學微分方程(1)的右端函數，其中發動機推力T=0。

滑行段初始狀態已知：

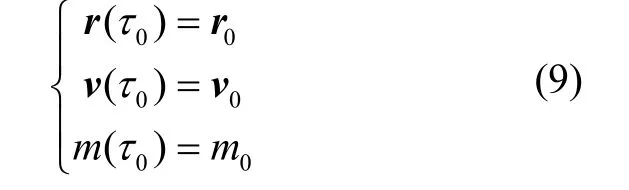
1.3 動力段離散建模

動力段設置N2個離散點，離散時間間隔為：

采用一階保持器的動力段均勻離散模型如下[10]：

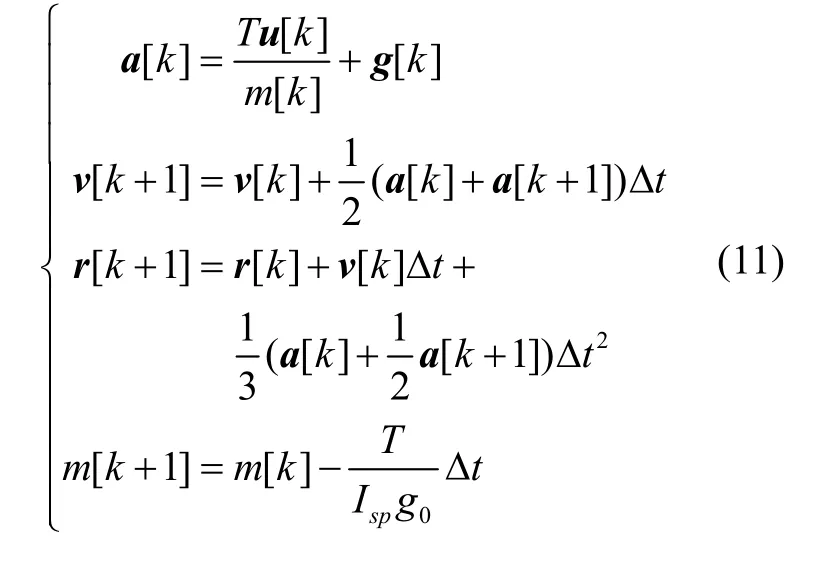
動力階段有式(3)所示推力矢量約束。飛行過程中狀態量連續，階段間連接約束為：

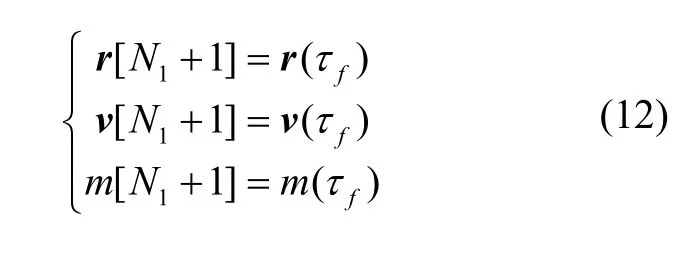
因為火箭發動機耗盡關機，終端約束除式(4)的入軌條件外還有終端確定質量約束：

通過上述分段離散，控制量加入發動機開機時間ts，解決了終端時間不確定問題，將經過離散后的模型稱為問題1。

2 推力方向約束無損凸化

問題1 中動力段推力大小恒定，推力矢量等式約束為球面非凸可行域，對該約束進行無損凸化，即將問題的非凸可行域進行適當松弛放大構成新的凸可行域，針對本文形成的球面可行域進行如下松弛變換：

僅當式(14)取等號時該約束為積極約束，與原問題等價。通過龐特里亞金提出的極大值原理可證明，松弛后問題最優解仍滿足原問題可行域約束，即松弛后子問題最優控制分量時刻滿足。

本文所研究的固體運載火箭，其推力大小不可調節，動力段質量變化與狀態量和控制量無關，在每個制導周期內質量為常量，在整個動力段線性時變[11～13]，因此證明中將質量看作常量，同時需要增加動力段時長等式約束,ΔTburn為動力段發動機工作時長。

模型描述：

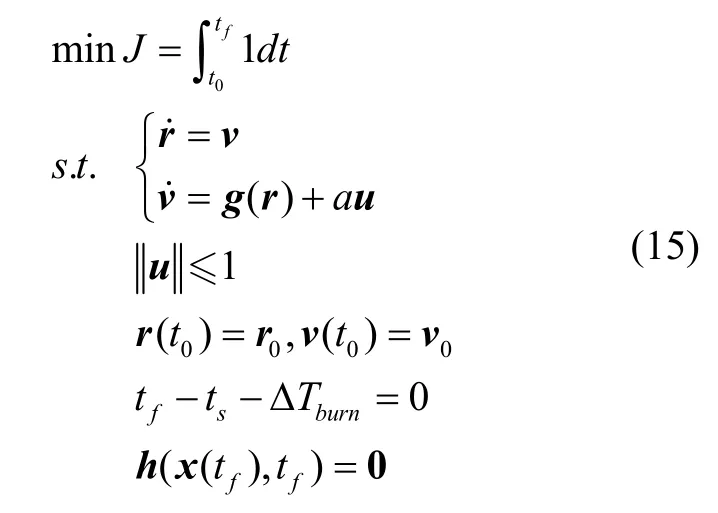
證明：

松弛后最優控制問題的哈密頓函數：

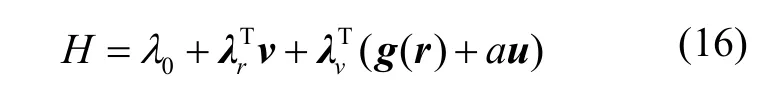
最優控制問題存在終端狀態和時間約束，終端函數為：

協態方程：

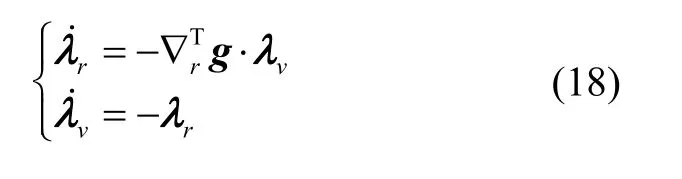
極大值條件：

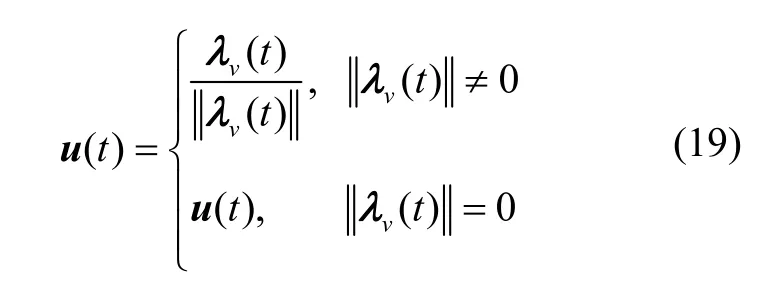
控制約束松弛條件：

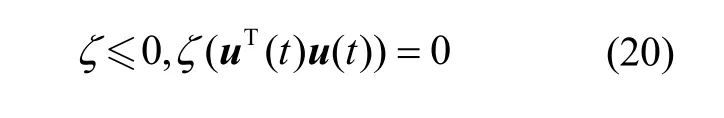
由于終端時間受約束，哈密頓函數：

根據終端函數可知哈密頓函數跳變條件：

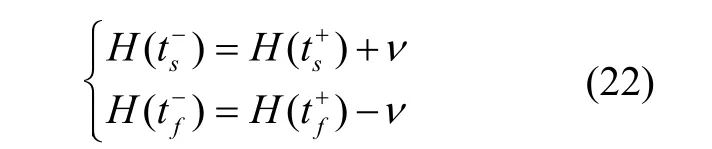
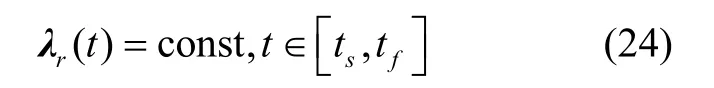
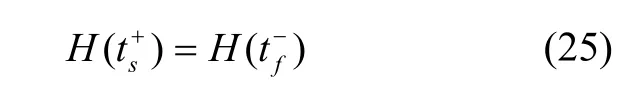
將式(22)中兩式相加，并結合式(25)可得：

又因該最優控制問題末端時間自由，終端時刻哈密頓函數為零，即：

由式(26)可知：

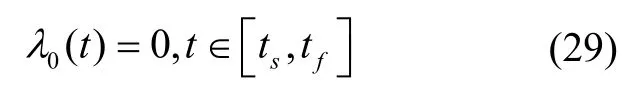
3 序列凸優化算法

問題1 非凸性除了推力分量約束形成的球面可行域外，還有非線性動力學方程和終端入軌非凸等式約束。利用線性化方法，問題1 將轉化成二階錐規劃問題，繼而可利用凸優化算法求解。

3.1 動力學方程線性化

針對非線性動力學方程中的非凸約束，通過在上一次迭代結果處進行一階泰勒級數展開，將其轉化成凸約束，通過迭代，結果將逐漸逼近原問題最優解[14]。

問題1 中滑行段動力學方程左端矩陣D是常數矩陣，將右端增廣非線性函數進行一階泰勒級數展開：

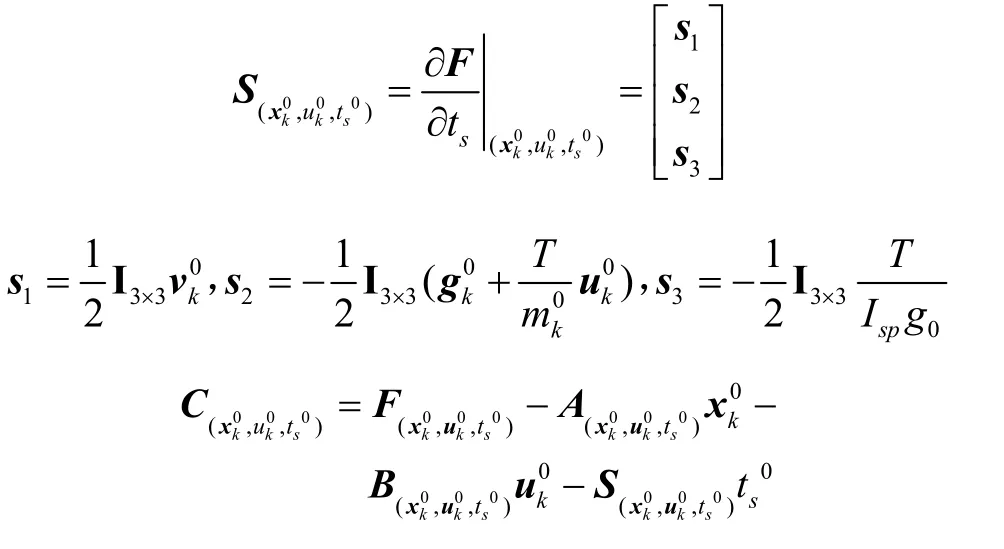
動力段運動方程進行一階泰勒級數展開，形式與滑行段類似。

3.2 終端約束線性化

運載火箭入軌時終端約束為關于狀態的非線性非凸等式約束，在終端時刻對式(4)進行一階泰勒級數展開：

3.3 序列凸優化問題及其求解

問題1 經過線性化和無損松弛，得到序列二階錐規劃問題：

1）松弛因子

經過上述凸化后的子問題，稱為問題2，在迭代求解初期，由于線性化產生的偏差，可能會造成“偽不可行”，即原問題存在可行解，但線性化后問題不可行。因此對問題2 中動力學方程（以滑行段為例）和終端約束添加松弛因子[15]：

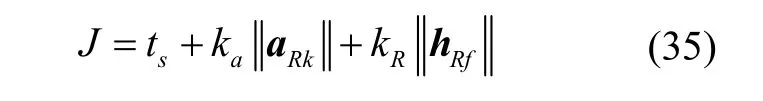
2）信賴域

利用序列凸優化算法對問題2 迭代求解時，每一次都選擇上一次迭代結果作為本次泰勒展開參考點，因此前后兩次求解結果必須滿足小偏差約束，否則會導致子問題線性化帶來誤差過大從而迭代失敗。引入第i次和第i+1 次變量迭代結果的信賴域約束：

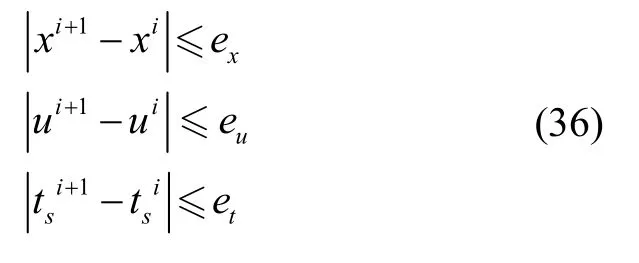
3）初值生成

迭代開始需提供初始狀態序列，良好的初始軌跡有利于迭代的快速收斂[16,17]。本文所研究的入軌問題末端狀態受等式約束，設計如下初值生成策略：首先選擇點火時間初值，在動力段，令俯仰角為時間的線性函數，偏航角恒定，得到姿態角曲線為：

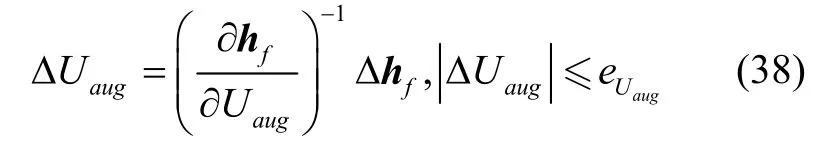
4 仿真校驗

選擇某固體運載火箭的第三級子火箭作為仿真對象，使用改進序列凸優化算法和LGR 偽譜法，對比說明本文所提出的改進序列凸優化算法的有效性和高效率。火箭發動機參數如表1所示，地心慣性系下初始狀態和終端入軌約束如表2所示，目標軌道為圓軌。

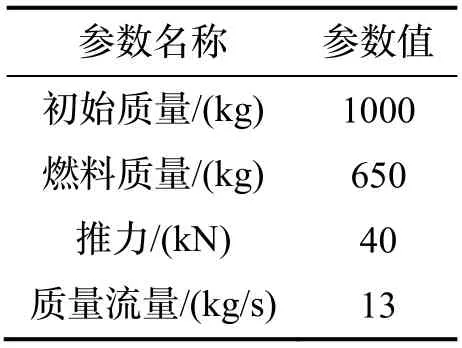
表1 火箭參數Tab.1 The rocket parameters

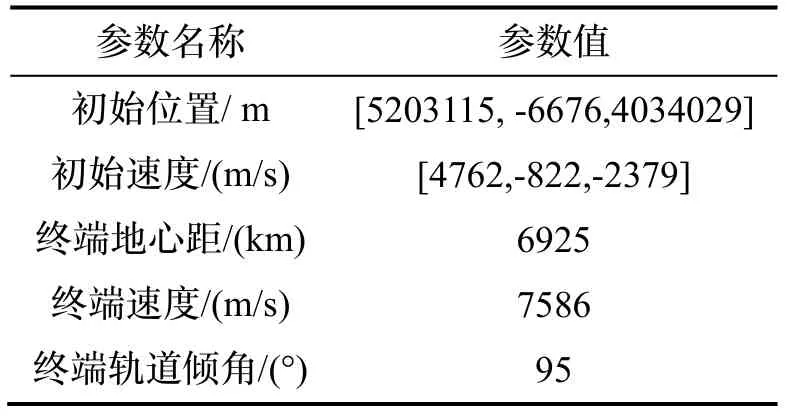
表2 初始狀態和終端約束Tab.2 Initial state and terminal constraints

本文數值計算在i7 3.6 GHz 筆記本電腦下進行，程序均在MATLAB 2014a 環境下編譯運行，采用CVX工具箱和SDPT3 求解器進行解算。

4.1 仿真結果

滑行段設置40 個LGR 離散點，動力段設置20個離散點，火箭滑行段時長作為性能指標，優化得到滑行時間為160.2 s，動力飛行50.0 s。

圖1 滑行+動力段三維軌跡Fig.1 Three dimensional trajectory of sliding and power segments

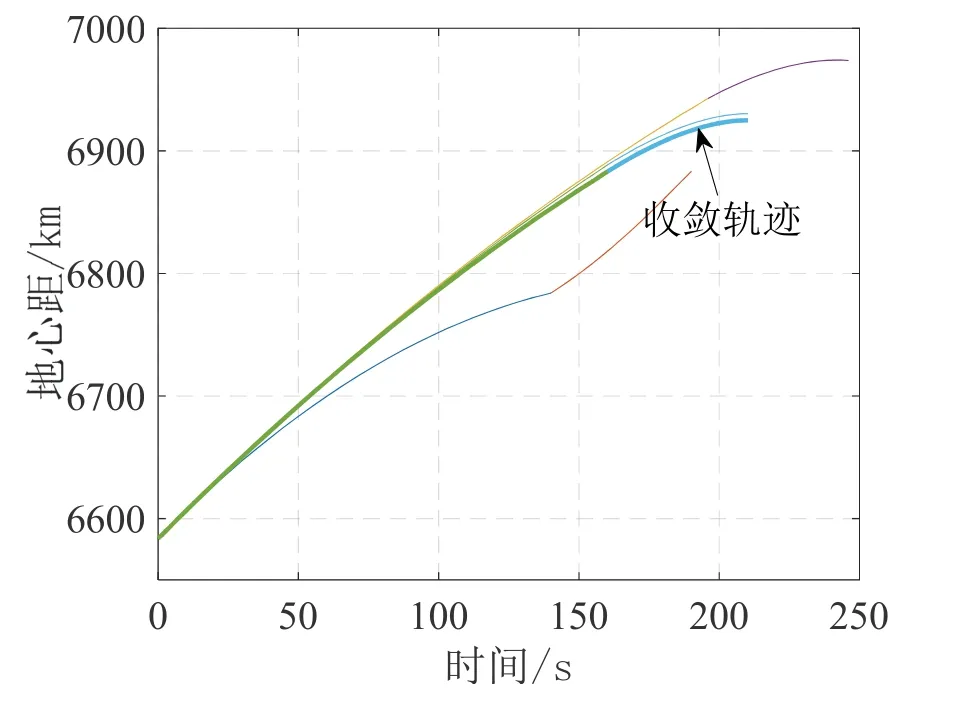
圖2 地心距隨時間變化曲線Fig.2 Geocentric distance curve over time

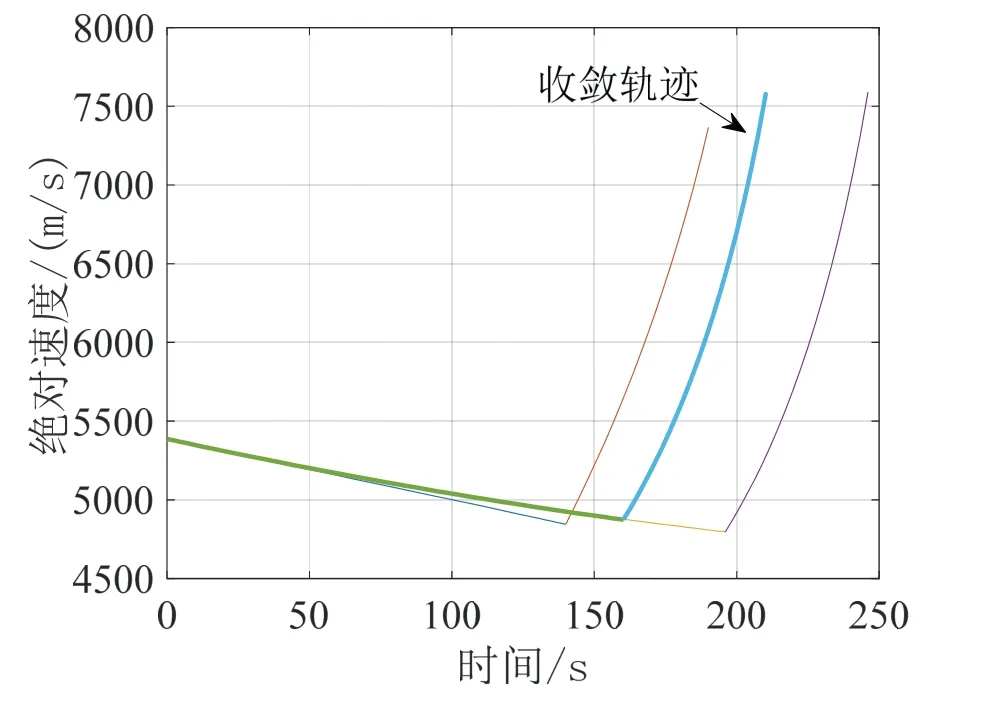
圖3 速度隨時間變化曲線Fig.3 Velocity curve over time

圖1是改進序列凸優化算法迭代得到的三維軌跡，圖2、3分別為各次迭代得到的飛行過程中地心距和速度變化曲線，最終得到的滿足收斂誤差閾值的軌跡在圖中標出。火箭耗盡關機時，滿足終端軌道約束。

圖4 松弛量變化曲線Fig.4 Relaxation curve

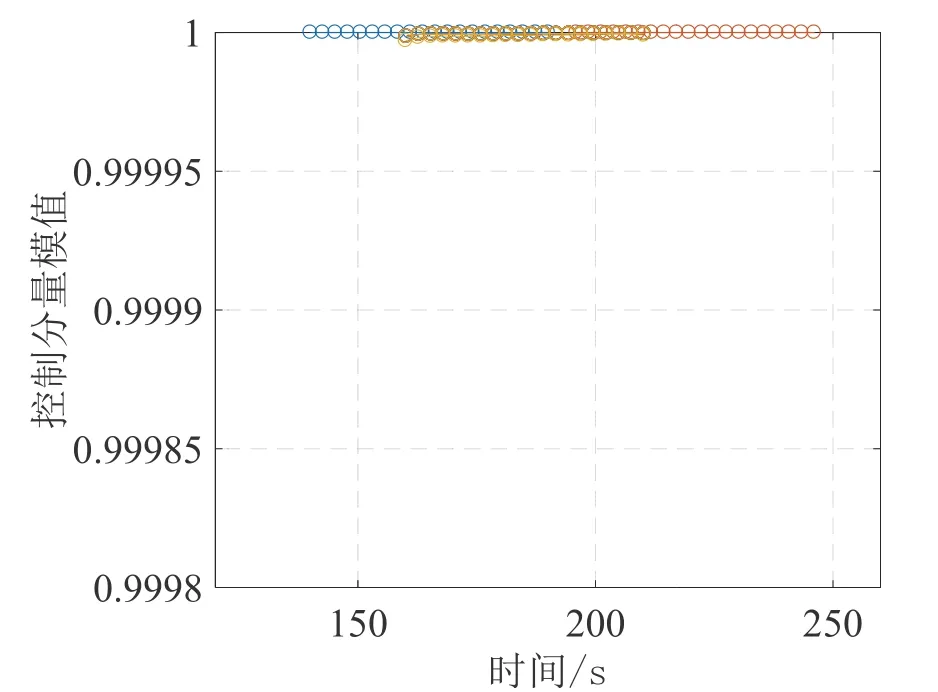
圖5 推力方向模值變化曲線Fig.5Thrust vector modulus curve

圖4中松弛因子隨迭代次數增加趨近于0，最終小于10-9，說明序列凸化求解結果與原問題最優解等價性。圖5為動力段推力方向模值，可以發現始終滿足，驗證結論1。

4.2 求解精度與效率分析

使用本文提出的初值生成器，耗時0.12s構建初始軌跡，得到的初始軌跡滑行時長為155.72s，終端地心距誤差為0.6km，終端入軌速度誤差為21.76m/s，終端當地速度傾角誤差為0.056 rad，終端軌道傾角誤差為0.0071rad。改進序列凸優化算法優化后的終端地心距誤差為0.22m，速度誤差為-0.063m/s，當地速度傾角誤差為0.00047rad，軌道傾角誤差為-0.00023rad，火箭成功入軌，驗證本文提出的改進序列凸化方法的可行性。

圖6-7為采用序列凸優化算法和偽譜法求解得到地心距、速度變化曲線對比，兩種方法計算結果吻合，說明本文所提的改進序列凸優化算法在實現高精度入軌上的有效性。

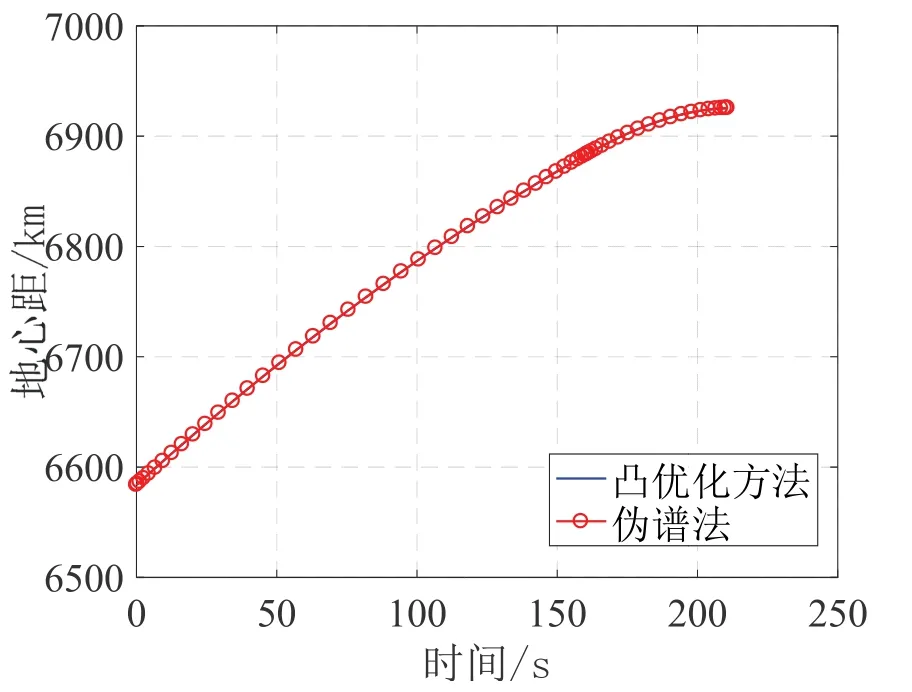
圖6 凸優化方法和偽譜法地心距變化Fig.6 Geocentricvariation by convex optimization and pseudospectral method

圖7 凸優化方法和偽譜法速度變化Fig.7 Velocity variation by convex optimization and pseudo spectralmethod

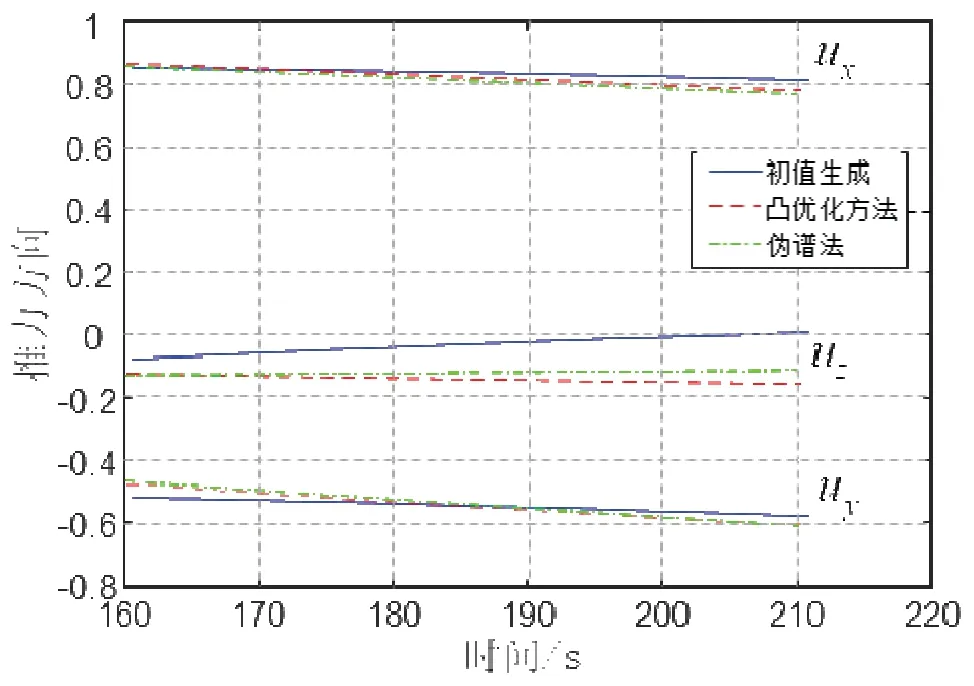
圖8 凸優化方法和偽譜法控制分量變化Fig.8 Thrust vector by convex optimization and pseudo spectralmethod

圖8為分別采用初值生成器、凸優化方法和偽譜法得到的發射慣性坐標系下動力段發動機推力方向曲線，可以發現凸優化方法和偽譜方法仿真得到結果基本吻合。

采用改進序列凸優化算法經過5次迭代結果收斂，每次迭代中求解凸優化子問題單步CPU 時間平均為0.16 s，模型初始化到得到收斂結果共耗時7.96 s，而偽譜法耗時118.42 s，改進序列凸優化算法計算效率相較于LGR 偽譜法,求解時間縮短了93.2%，具有顯著優勢。

5 結論

本文針對耗盡關機固體運載火箭入軌段制導問題，提出一種改進序列凸優化算法，以滑行段時長為優化指標，規劃點火時間和動力段推力方向，實現火箭耗盡關機時精確入軌，通過仿真驗證得到主要結論如下：

利用LGR 偽譜法進行時域映射，將發動機開機時間作為新的控制變量，解決了點火時間不確定問題，保證了滑行時長的最優性。

針對推力方向非凸球面約束，通過松弛轉化為凸的球體約束，并在理論上證明松弛手段的無損性；將非凸的動力學方程和終端狀態等式約束在參考軌跡上進行線性化，從而將其轉化為凸約束，利用序列凸優化算法，結合松弛因子和信賴域等迭代策略，使構建的凸優化子問題最優解逼近原問題最優解。

含初始軌跡生成器的序列凸優化算法求解本文研究的入軌制導問題時間僅為偽譜法的6.72%，解算結果終端地心距誤差為0.22 m，速度誤差-0.063 m/s，當地速度傾角誤差為 0.00047 rad，軌道傾角誤差為-0.00023 rad，驗證本文所提出的改進序列凸優化方法解決耗盡關機固體火箭入軌制導問題的有效性。