基于最小均方算法的半球諧振子特征參數辨識方法

郜中星，徐睿東，張勇剛

（1.哈爾濱工程大學物理與光電工程學院，哈爾濱 150001；2.哈爾濱工程大學智能科學與工程學院，哈爾濱 150001）

半球諧振陀螺（hemispherical resonator gyro，HRG）是一種基于科氏效應的固體波動陀螺，在高精度、高可靠性和抗輻射等方面具有突出的優勢[1]，可以滿足軍用領域和民用領域的多種傳感需求。半球諧振子（hemispherical shell resonator，HSR）作為半球諧振陀螺的核心元件，其各向異性的程度與工作在全角模式下的陀螺性能密切相關。半球諧振子周向的剛度分布不均勻，會導致駐波的波形綁定和頻率裂解現象，而周向的阻尼（或品質因數）分布不均勻，會導致駐波方位角向阻尼較小的方向漂移并自鎖[1]。通常，用于表征半球諧振子的特征參數主要包括：剛度各向異性Δω，剛度失準角，阻尼各向異性 Δ(1 /τ)，阻尼失準角[2]。目前，可以通過離子束或激光調平等方法將剛度分布不均勻抑制到最小程度（可小于0.5 mHz），但殘余的頻率裂解仍會對陀螺的靈敏度等性能產生影響。而阻尼分布不均勻目前尚缺乏有效手段進行處理，因此成為了制約全角半球諧振陀螺精度提升的關鍵因素[3,4]。綜上，對半球諧振子的四種特征參數進行辨識不僅可以為陀螺的性能評估提供參考，還可以為全角半球諧振陀螺漂移誤差和標度因數誤差的補償提供依據。

S.L.Li 等[5]提出了根據駐波進動效應的周期來求解半球諧振子頻率裂解的方法，但求解的分辨率和有效性會受到半球諧振子品質因數的制約。I.P.Prikhodko 等[6]研究了在全角半球諧振陀螺中由阻尼各向異性引起的角度漂移會隨著外界輸入轉速的增加而呈現線性減小的現象，并提出了通過高速虛擬旋轉來減小阻尼各向異性的影響。P.Taheri-Tehrani 等[7]提出了利用非理想諧振子振動方程來求解阻尼各向異性Δ(1 /τ)的方法，但該方法需要將化簡后的振動方程與角度測試數據進行擬合來提取 Δ(1 /τ)，因而會引入較全文的結構安排如下：首先，根據非理想半球諧振子在橢圓坐標系下的運動方程，對全角半球諧振陀螺的工作原理和控制系統進行了介紹；然后，根據非理想半球諧振子的正交誤差方程和駐波方位角誤差方程，構建了基于LMS 算法的特征參數辨識模型；最后，基于Simulink 工具箱搭建了全角半球諧振陀螺的多參數仿真平臺，利用該平臺仿真驗證了所提出辨識方法的有效性。

1 全角半球諧振陀螺的工作原理和控制系統

理想條件下，半球諧振子可以等效于進行簡諧運動的質點。然而，真實系統中會存在由各向異性引起的剛度和阻尼耦合誤差項，因此對非理想的半球諧振子在直角坐標系下的運動方程進行如下描述[9]：

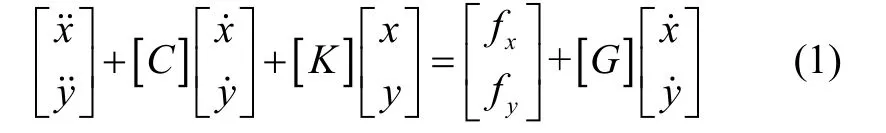
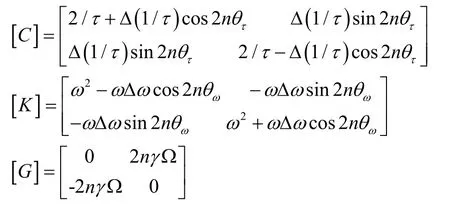
式(1)中，x和為諧振子在x模態上的位移和驅動力，y和為諧振子在y模態上的位移和驅動力。Ω 為外界輸入的角速度，0.27γ≈為諧振子的進動因子，2n=為振型階數。大誤差。Z.X.Hu 等[8]提出了采用擴展卡爾曼濾波（EKF）來對半球諧振子特征參數進行估計的方法。該方法雖然具有較高的識別精度，但EKF 算法對樣本數據的穩定性要求很高，因此需要半球諧振子具有很小的各向異性才能估計準確。綜上，通過簡單有效的方法快速估計出半球諧振子的特征參數，對于陀螺誤差的補償以及性能的提升將具有重要意義。

本文提出了一種基于最小均方（least mean square，LMS）算法的半球諧振子特征參數辨識方法。

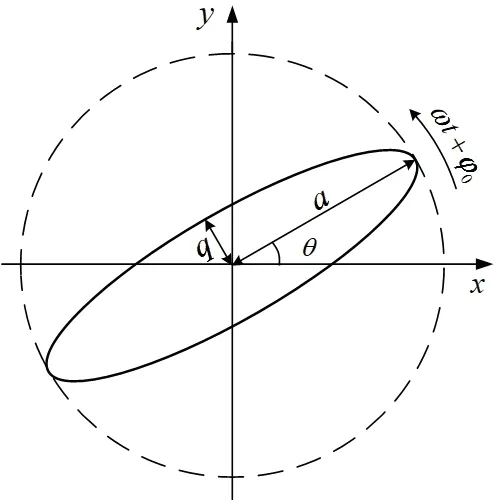
圖1 二維諧振子的運動軌跡Fig.1 Motion trajectory of the two-dimensional resonator

二維諧振子的運動軌跡如圖1所示[10]，在科氏力作用下半球諧振子的振型相對于安裝基座以γ-Ω 的角速度圍繞中心反向旋轉。根據圖1，x模態軸與y模態軸上的位移表達式為：

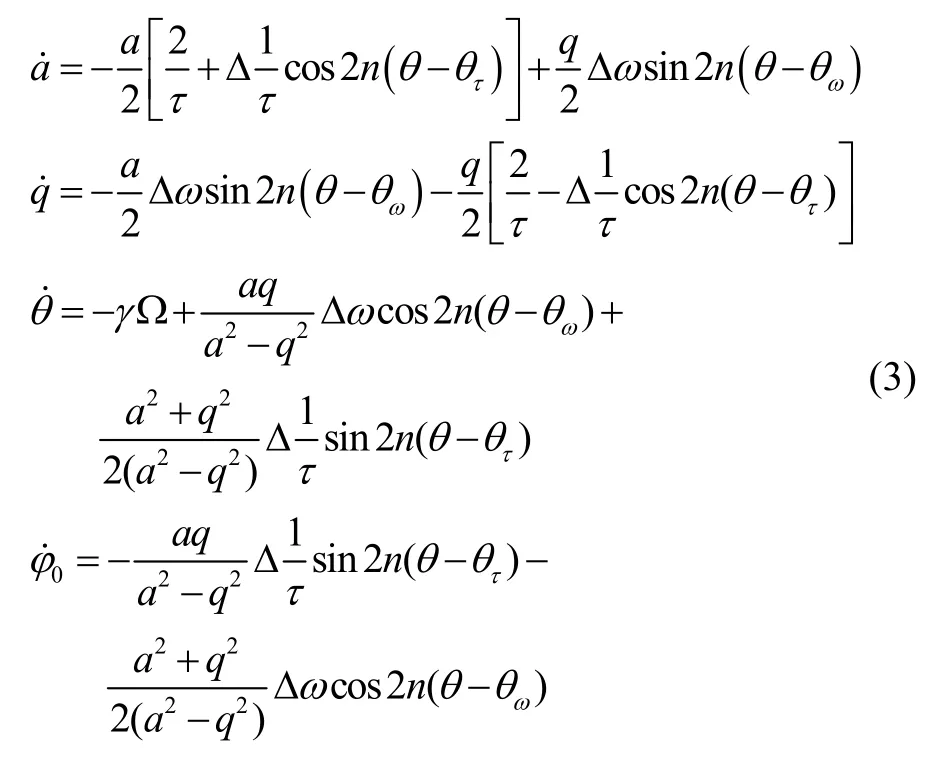
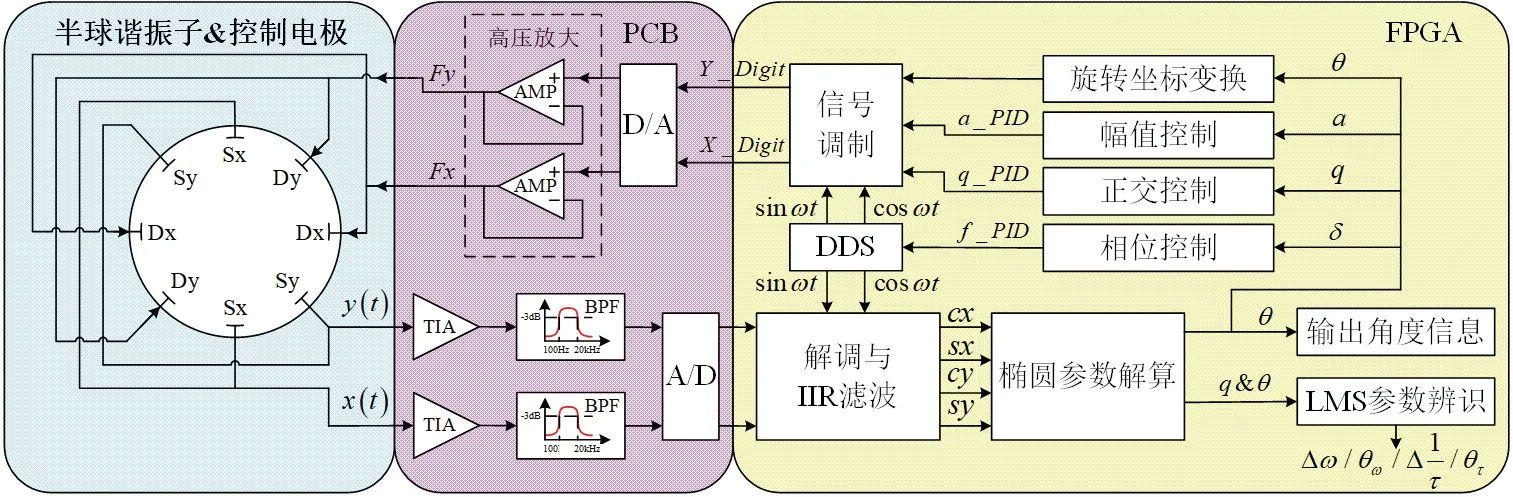
圖2 全角半球諧振陀螺的控制系統框圖Fig.2 Block diagram of HRG control system with whole-angle mode operation

全角半球諧振陀螺的控制系統框圖如圖2所示。為了提高檢測信號的信噪比，模擬前端使用了跨阻放大、帶通濾波等方法對檢測信號進行處理。將處理后的檢測信號與DDS 產生的參考信號進行乘法解調，經過IIR 濾波后得到用于橢圓參數解算的四個有效信號分別為：cx、sx、cy、sy。再代入到參數解算方程(4)中分別得到半球諧振子的橢圓參數為：a、q、θ、δ[12]。

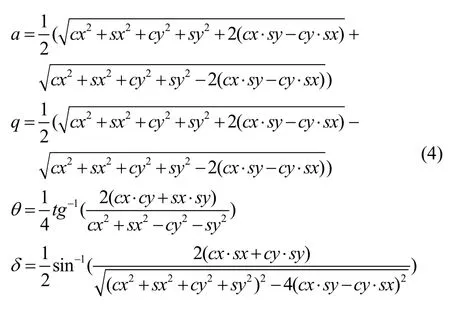
其中，通過對θ進行旋轉坐標變換來實現驅動力與駐波方位角的對準；通過對a進行PID 幅值控制產生 _a PID信號來維持振幅穩定；通過對q進行PID 正交控制產生 _q PID信號來抑制正交誤差；通過對δ進行PID 相位控制產生 _f PID信號來保證參考信號與檢測信號的相位差恒定。對以上四個環節的輸出信號通過調制產生驅動信號，最后將驅動信號施加到驅動端電極可以得到驅動力信號Fx,Fy。以上各個環節共同構成了全角半球諧振陀螺控制系統的一個完整信號環路。

2 基于LMS 算法的特征參數辨識模型建立

非理想半球諧振子在橢圓坐標系下的正交誤差方程為式(5)所示。

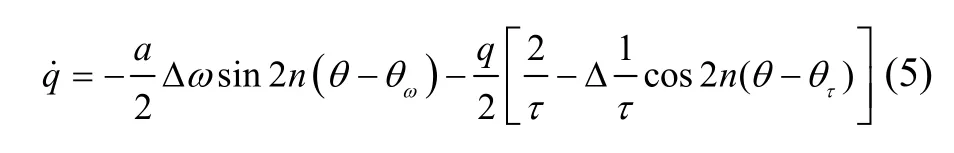
對陀螺不施加正交控制，雖然此時q不為0，但正交信號仍遠小于幅值信號即q a?，則式(5)可以簡化為式(6)的形式。可以看出，式(6)僅含有半球諧振子特征參數中Δω和的信息，避免了參數辨識過程中與 Δ(1 /τ)和產生耦合。

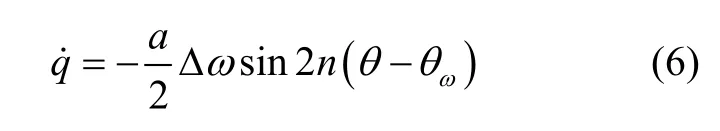
將式(6)進一步展開可以得到：

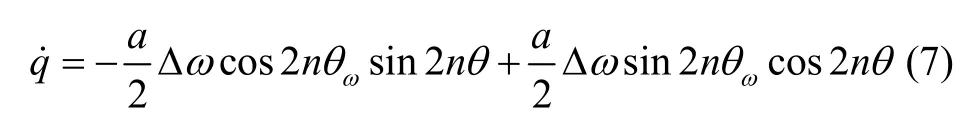
下面，基于LMS 算法構建關于ωΔ 和的參數辨識模型，令：

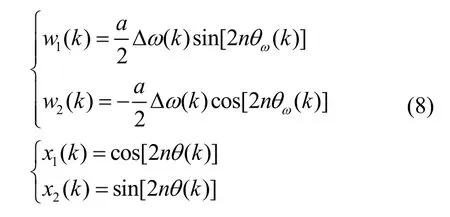
則可以得到：

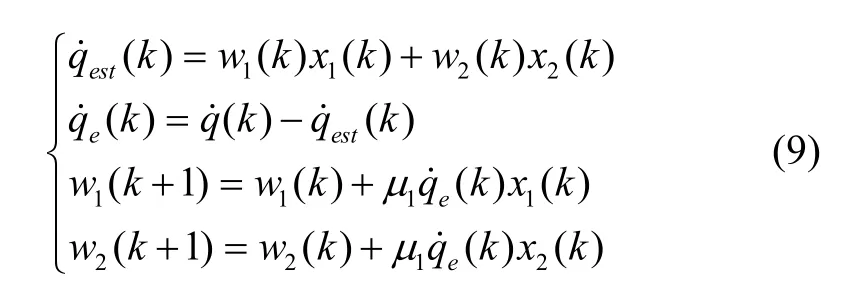
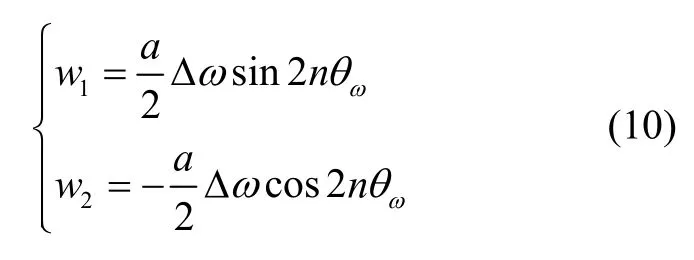
根據式(10)的估計結果，可以得到剛度各向異性ωΔ 和剛度失準角的辨識結果分別為：

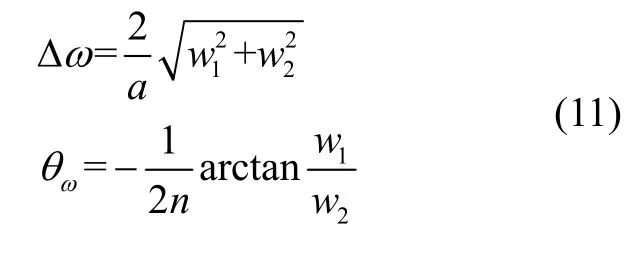
非理想半球諧振子在橢圓坐標系下的駐波方位角誤差方程如式(12)所示。

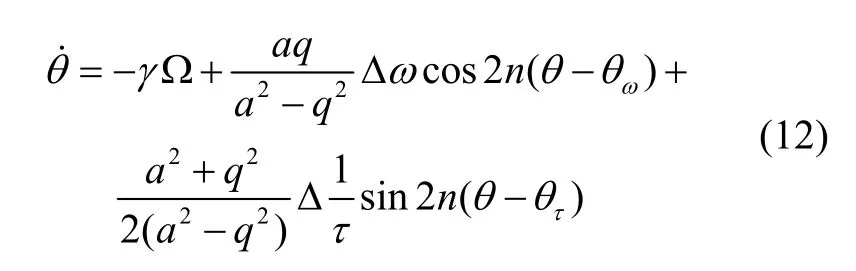
對陀螺施加正交控制，此時q被抑制到0，則式(12)可以簡化為式(13)的形式。可以看出，式(13)僅含有半

球諧振子特征參數中(1/)τΔ和的信息，避免了參數辨識過程中與ωΔ 和產生耦合。

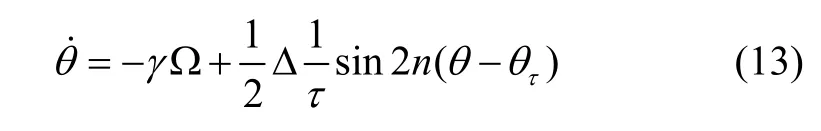
將式(13)進一步展開可以得到：

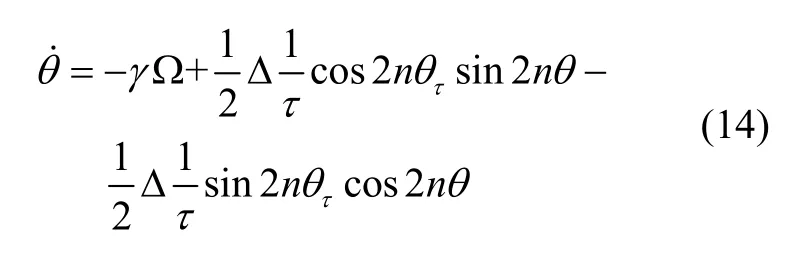
下面，基于LMS 算法構建關于(1/)τΔ和的參數辨識模型，令：

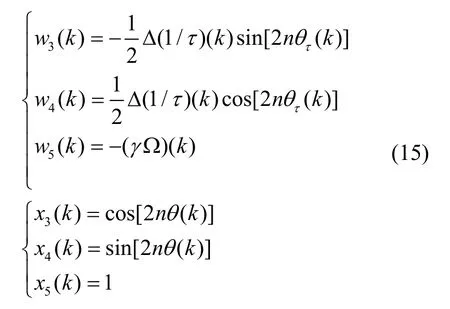
則可以得到：

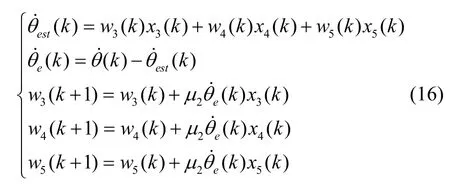
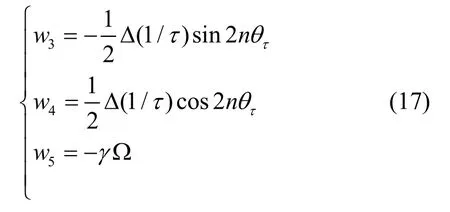
根據式(17)的估計結果，可以得到阻尼各向異性Δ(1/τ)和阻尼失準角的辨識結果分別為：

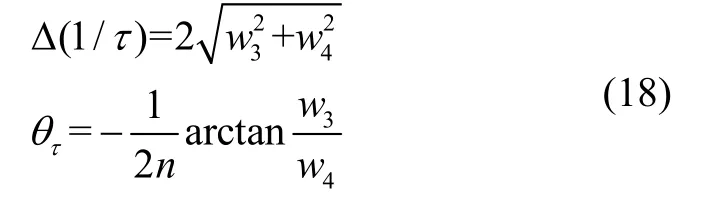
式(5)-(18)給出了基于LMS 算法對半球諧振子進行特征參數辨識的過程，通過優化以及轉速激勵Ω 的選擇，可以進一步提高辨識精度和辨識速度。

3 仿真驗證與結果分析

為了驗證所提出的特征參數辨識方法的有效性，利用Simulink 工具箱搭建了全角半球諧振陀螺的多參數仿真平臺，如圖3所示。通過不同的參數設定，可以仿真分析半球諧振子的各種運動規律。其中：非理想半球諧振子模塊包含了式(1)中需要辨識的四種特征參數；電容檢測模塊包含了C/V 轉換、帶通濾波與A/D 轉換；信號解調模塊包含了參考信號與檢測信號的乘法解調和數字低通濾波器；橢圓參數解算模塊用于半球諧振子橢圓參數a、q、θ、δ的解算；信號調制模塊包含了幅值控制、正交控制、相位控制以及旋轉坐標變換；最后，靜電驅動模塊包含了D/A 轉換與高壓放大。

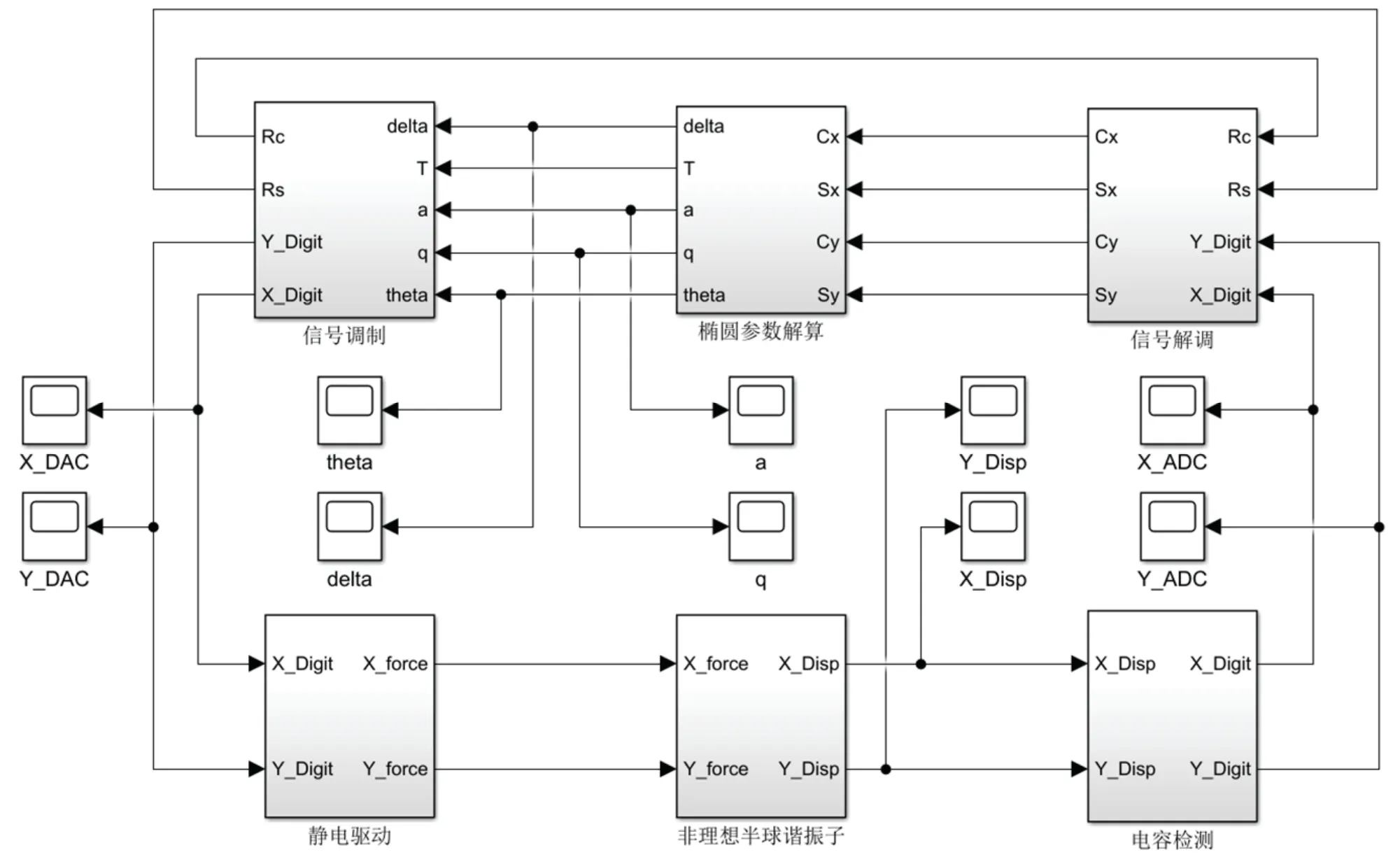
圖3 全角半球諧振陀螺仿真模型Fig.3 Simulation model of HRG with whole-angle mode operation

表1 列出了用于驗證所提出辨識方法的轉速激勵條件和半球諧振子特征參數。可以計算得到對應的Δω和 Δ(1/τ)分別為：。

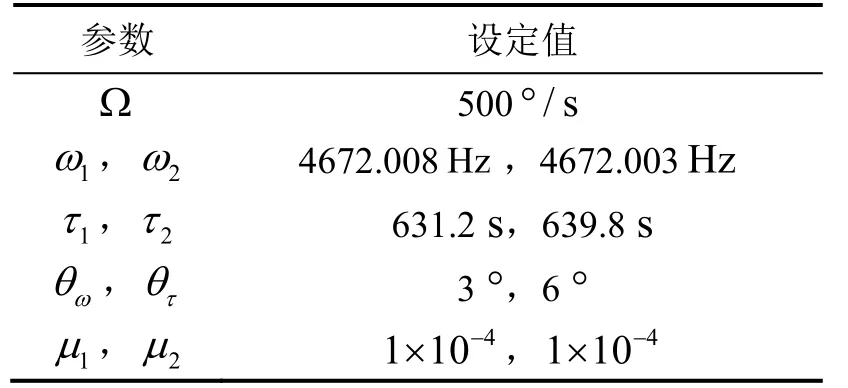
表1 仿真參數設置Tab.1 Simulation parameters of HRG

通過圖3所示的Simulink 程序得到正交分量q的數據集和駐波方位角θ的數據集，同時利用所提出的基于LMS 算法的辨識模型，圖4 和圖5 分別給出了半球諧振子特征參數的辨識結果。可以看出，半球諧振子的四個特征參數全部在8 s 以內辨識出來，并且全部收斂于設定值，從而仿真驗證了所提出方法的有效性。通過優化LMS 的算法步長，可以實現更精確、更快速的辨識。

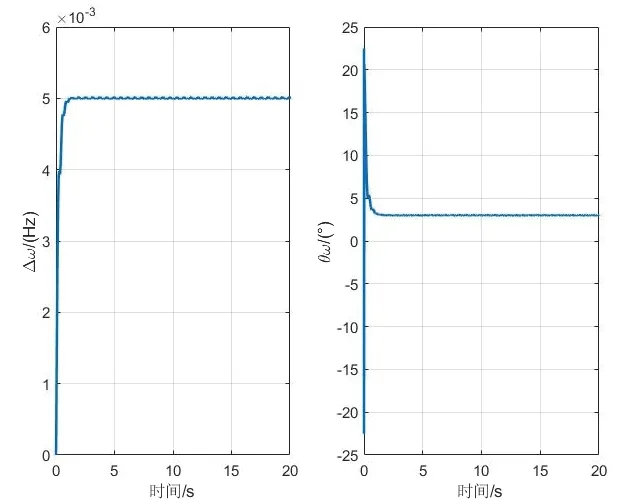
圖4 ωΔ 和的辨識結果Fig.4 Identification results of ωΔ and

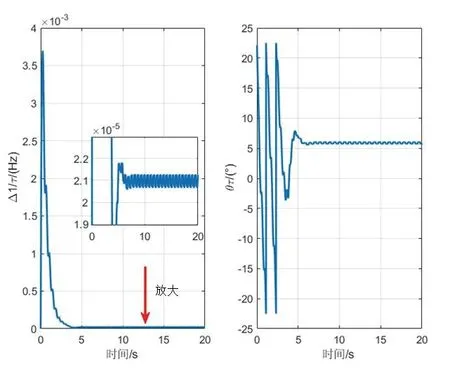
圖5 和的辨識結果Fig.5 I dentification results of and

4 結論

本文根據非理想半球諧振子在橢圓坐標系下的正交誤差方程和駐波方位角誤差方程，構建了基于LMS算法的半球諧振子特征參數辨識模型。根據全角半球諧振陀螺工作原理，基于Simulink 搭建了全角半球陀螺控制系統的仿真平臺。仿真結果表明，所提出的辨識方法能在8s 內辨識出半球諧振子的剛度各向異性、剛度失準角、阻尼各向異性和阻尼失準角，從而實現了快速且準確的特征參數辨識。下一步的工作將會利用半球諧振陀螺實際采集的數據集對所提出的參數辨識方法進行實驗驗證，同時研究特征參數的在線辨識方法，從而實現半球諧振陀螺輸出誤差的實時校準與補償。