原子力顯微鏡在二維材料力學性能測試中的應用綜述1)

高揚

(浙江大學工程力學系,杭州 310027)

1 引言

1.1 二維材料及其力學表征

二維材料是指僅僅由單原子層構成的平面材料[1-3].石墨烯是最早被發現的二維材料,由英國曼徹斯特大學Geim 和Novoselov[4]在2004 年通過透明膠帶機械剝離石墨所得到.另外值得注意的是,同年美國佐治亞理工學院的de Heer[5]也通過碳化硅表面外延生長的方式得到了單層石墨結構并進行了細致的表征.但是“石墨烯”的概念卻是由Geim 首先提出的,Geim 和Novoselov 也在2010 年獲得了諾貝爾物理學獎.二維材料之所以受到極大的關注,一方面是長久以來統計力學中“非零溫情況下不存在理想的二維晶體”這個大家認可的共識被石墨烯打破;另一方面,以石墨烯為代表的二維材料本身也展現出了迥異于其對應的塊體材料的優異性質[2-9].例如石墨烯的遷移率高達104cm2/(V·s),電子在狄拉克點附近呈現線性色散關系,同時在石墨烯中觀測到了半整數量子霍爾效應,這些都是石墨所不具備的新穎物理現象[4,8-9].除了石墨烯,以二硫化鉬MoS2為代表的二維過渡金屬硫族化合物(TMDC)由于天然的空間反演對稱性破缺,與石墨烯零帶隙的結構不同,單層時直接帶隙大小普遍在1 ～2 eV 之間[10-11].以單層MoS2為原材料制備得到的二維場效應晶體管的開關比在常溫時高達108,達到甚至超過了傳統硅基邏輯芯片的標準,被認為是下一代集成電路芯片材料的有力候選[12].如果說石墨烯和二硫化鉬分別代表了二維材料的第一和第二波熱潮,那么以磷烯phosphorene(或者黑磷black phosphorus)為代表的其他非碳二維材料可以被認為是二維材料研究的第三波熱潮[13-16].磷原子最外層有5 個價電子,能夠與近鄰的3 個磷原子形成sp3雜化鍵,因此不同于平坦的石墨烯,磷烯的表面褶皺起伏同時還展現出明顯的平面內各向異性[17-18].不過值得注意的是,目前大多數關于二維材料的研究和報道主要聚焦于其電學、光學和磁學性質及其相關應用,對其力學性質的研究則相對缺乏[19].而作為材料科學中的最基本的物理性質之一,對于二維材料力學性質的探索除了基礎研究的需要,另外一方面也是二維材料從實驗室走向具體應用中不可或缺的重要步驟.例如柔性電子器件對二維材料對拉伸、彎曲等外界載荷的響應提出了新的要求,而航空航天和軍事領域則要求對二維材料在極端力學環境(如高壓、沖擊、爆炸、超高溫)中的相變行為或者性質變化有清晰的認知[20].

當前對二維材料力學性質的研究主要集中于彈性模量、泊松比、斷裂強度、摩擦潤滑、吸附力、高壓相變等方向[19,21-22].微納壓痕技術(micro/nanoindentation)是傳統的表征宏觀塊體材料力學性質的重要測量手段[23-27].通過控制正壓力的大小,可以使材料發生相應的彈性/塑性形變,從而得到對應的力學參數.原子力顯微鏡的針尖半徑一般小于100 nm,壓電陶瓷可以將壓印形變控制到10 nm 以下,因此很自然地被研究人員用于測量納米級二維材料的力學性能[28].在引言的第二小節,簡單介紹了原子力顯微鏡的工作原理和發展歷史;在第二部分中將進一步闡述基于原子力顯微鏡的納米壓痕技術的工作原理和具體實例,并討論測量中可能存在的誤差與來源.

狹義的二維材料正如本文開始所提到的,特指僅僅由單原子層組成的晶體.但是研究人員發現多層的二維材料往往也具有和單層二維材料相似的性質.特別的是,多層二維材料在某些方面甚至具有單層二維材料不具備的特性,其根源便在于層間的范德華作用力.通過調節層間范德華作用力來調控二維材料的各種性質已經成為當下熱門研究課題.二維材料又被稱為范德華材料,其層間距普遍小于1 nm(例如石墨烯是0.34 nm,二硫化鉬是0.65 nm),因此若要精確地測量范德華材料的層間力學性質而不受面內彈性模量的干擾,則要求壓印形變小于范德華材料的層間距,對此通過納米壓痕技術來實現較為困難.為了解決這個問題,最近研究人員開發了同樣基于原子力顯微鏡的埃(?)壓痕技術(angstrom-indentation),通過間接測量+積分的方式,巧妙地將壓印形變降低到了1 nm 以下,精度達到了0.1 ?,完美適用于測量范德華材料的層間力學性質[29].在本文的第三部分中,作者將詳細闡述埃壓痕技術的原理和應用.最后,簡要介紹了一種新型的范德華材料?范德華異質結,即不同的二維材料通過層間范德華作用力實現的垂直堆疊.同時簡要討論了埃壓痕技術在范德華異質結力學性質研究中的潛在應用.

1.2 原子力顯微鏡

原子力顯微鏡(atomic force microscopy,AFM)是在掃描隧道顯微鏡(scanning tunneling microscopy,STM) 的基礎上由IBM 在1986 年發明的,原子力顯微鏡和掃描隧道顯微鏡被合稱為掃描探針顯微鏡(scanning probe microscopy,SPM)[30].原子力顯微鏡的基本結構如圖1(a) 所示,核心結構是由懸臂梁和針尖組成的探針,探針的運動通過壓電陶瓷來控制.激光束照射在懸臂梁的背面并反射到由光敏二極管陣列組成的激光探測器上,因此懸臂梁的微小彎曲通過光路實現了放大和接收.原子力顯微鏡最基礎的測量模式是“接觸模式”.在接觸模式的實際測量過程中,針尖接觸樣品表面并且水平移動,樣品表面的高低起伏引起的懸臂梁彎曲程度的變化被激光探測器檢測到,控制器內部的反饋系統會自動調節壓電陶瓷的電流從而升高或降低懸臂梁和樣品的相對位置使懸臂梁的彎曲(即激光光斑在探測器上的位置)一直保持在預設值,壓電陶瓷的壓縮或伸張就蘊含了樣品表面形貌的具體信息.納米壓痕技術和埃壓痕技術都是基于原子力顯微鏡的接觸工作模式,因此原子力顯微鏡的其他工作模式(例如“敲擊模式”)在此不做贅述.

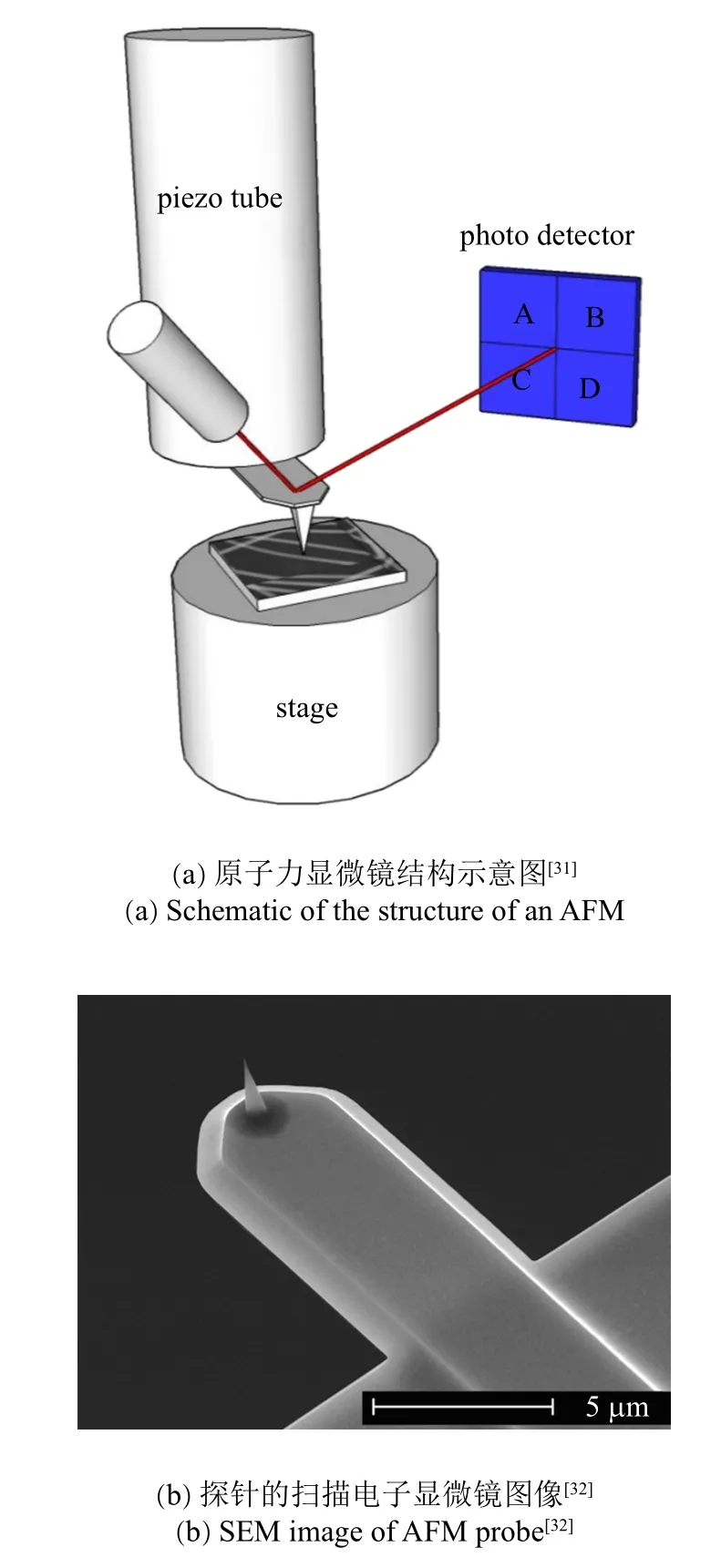
圖1 原子力顯微鏡Fig.1 Atomic force microscopy

2 納米壓痕技術和二維材料面內力學性質

2.1 懸空二維材料的面內拉伸測量

為了實現足夠大的拉伸應變,在納米壓痕實驗中,二維材料一般被置于懸空基底上,如圖2 所示.最早利用原子力顯微鏡測量二維材料力學性質是在2007 年,2 ～8 nm 厚的若干層石墨烯被置于寬度為1 μm 的長方形溝槽上,原子力顯微鏡的探針在石墨烯中間施加正壓力,產生垂直位移,從而引起面內拉伸[33].利用這種方式得到的若干層石墨烯的彈性模量為500 GPa,明顯低于理論預測值[34].美國哥倫比亞大學的Lee 等[35]對懸空石墨烯納米壓痕實驗做出改進,將單層石墨烯置于圓形孔洞上,針尖在二維薄膜中心施加點載荷,從而提供了相比長方形溝槽更對稱的應變分布,如圖2(c)所示.此后大多數二維材料的彈性力學測量都是基于相似的實驗裝置.通過控制針尖的位移,可以精確控制二維薄膜的形變,同時將激光探測器得到的光斑偏轉信號乘以探針懸臂梁的彈簧常數得到施加的正壓力,最終得到壓力?位移曲線,如圖3(a)所示.由于基底側壁與二維材料之間的范德華力的吸附作用,納米壓痕實驗一般被視為邊緣固定薄圓板在中心點載荷作用下彎曲的過程,連續介質力學理論給出壓力和位移的本構關系[35-37]

其中,F是針尖作用于二維材料薄膜正壓力,δ 是二維材料薄膜中心被針尖下壓的位移,r是圓孔的半徑,q是一個與二維材料的泊松比v相關的無量綱常數1/(1.05 ?0.15v?0.16v2).和E2D是二維材料的二維預應力和二維彈性模量.將式(1)對納米壓痕得到的壓力?位移曲線進行擬合,便可得到二維材料的二維預應力和二維彈性模量.如果將二維材料簡單認為是各向同性的,那么將二維彈性模量除以二維材料的厚度,便得到等效三維彈性模量.如果持續增大正壓力直到二維薄膜破裂,還可以得到二維材料的二維斷裂強度σm

其中,F是二維材料破裂時的正壓力,E2D是二維材料的二維彈性模量,R是原子力顯微鏡針尖的曲率半徑.

圖2 二維材料納米壓痕實驗示意圖Fig.2 AFM-based nano-indentation on 2D materials

2.1.1 石墨烯面內彈性模量

圖3(a)是懸空單層石墨烯的壓力?位移曲線和對應式(1)的擬合,擬合曲線與實驗結果十分接近.在多次重復納米壓痕實驗之后可得到如3(b)所示的二維彈性模量的統計直方圖,單層石墨烯的二維彈性模量約為(342±30) N/m.假設單層石墨烯的厚度為0.34 nm,Lee 等[35,38]得到單層石墨烯的三維等效彈性模量約為(1.0±0.1)TPa,二維斷裂強度約為55 N/m.1.0 TPa 的彈性模量與金剛石接近,基本達到了固體材料剛度(stiffness)的上限.值得注意的是,目前所有關于無支撐二維材料的力學性質的實驗工作都把二維材料簡單地視作連續的各向同性材料,然而二維材料具有明顯的各向異性,其面內和層間的力學性質是完全不同的.更嚴謹的表達是:此處所謂的“等效三維彈性模量”實質上是面內彈性模量E||,對應的是石墨烯層內碳原子之間的sp2雜化鍵的強度,因此石墨烯超高的面內彈性模量是結構穩定并且鍵能極高的碳碳sp2鍵的結果.考慮到石墨烯和其他大多數二維材料在面內具有很高的對稱性,我們可以在不失嚴謹性的前提下認為二維材料面內是近似各向同性的,因此二維材料又可以被視為面內各向同性材料(transversely isotropic materials).面內各向同性材料的應力張量σ和應變張量ε的關系可表達成

圖3 單層石墨烯的面內力學性質Fig.3 Transverse/in-plane elasticity of graphene

圖3 單層石墨烯的面內/面內力學性質(續)Fig.3 In-plane elasticity of graphene(continued)

決定面內各向同性材料的彈性性質的主要有5 個獨立參量,分別是

其中E||即二維材料的面內彈性模量,即納米壓痕實驗中得到的“等效三維彈性模量”,v是材料的泊松比,E⊥是二維材料的層間彈性模量,對應二維材料的層間范德華作用力的強度,Gyz即二維材料的層間剪切模量,代表了二維材料抵抗層間滑移的能力,又被稱為層間吸附強度.層間剪切模量的來源與層間彈性模量相同,即范德華作用[39-40].在本文第三部分將具體介紹用于測量二維材料層間彈性模量的方法和技術.

2.1.2 二硫化鉬面內彈性模量

和石墨烯相似,二硫化鉬也具有六方蜂巢晶格結構;不同的是二硫化鉬是化合物,由硫和鉬兩種元素組成,并且硫和鉬原子在層內不處于同一個平面,兩層硫原子之間夾著一層鉬原子,如圖4(a)所示.二硫化鉬由于其較弱的層間剪切模量(C44),在工業上一直被廣泛地用作潤滑劑.塊體二硫化鉬是間接帶隙半導體,而單層二硫化鉬則是直接帶隙半導體,帶隙約為1.8 eV,對應波長處于可見光范圍內,因此二硫化鉬被認為在光電材料領域有著誘人的應用前景.圖4(b)是機械剝離在多孔硅基底上的單層二硫化鉬,納米壓痕實驗的過程與石墨烯完全相同,在此不再贅述.納米壓痕實驗發現,單層二硫化鉬面內彈性模量約為270 GPa[41-43].

圖4 二硫化鉬Fig.4 MoS2

2.1.3 其他二維材料面內彈性模量

自石墨烯和二硫化鉬之后,二維材料家族迅速擴大,大量新型二維材料被發現和合成.例如有“白石墨烯”之稱的六方氮化硼(hexagonal boron nitride,h-BN) 的面內彈性模量達到了900 GPa[44];此外國際上多個課題組對其他過渡金屬硫族化合物(例如WS2,WSe2和MoTe2等) 和其他新型非碳二維材料(例如磷烯、GaS,Bi2Te3,WN 等)的面內力學性質也做了廣泛而深入的研究[45-52].文獻[50]中總結并展示了若干有代表性的報道,如圖5 所示.

圖5 部分二維材料面內彈性模量總結[50]Fig.5 In-plane Young’s moduli of representative 2D materials[50]

2.2 帶柔性可延展基底的二維材料的面內拉伸測量

二維材料在其他實驗和實際應用中往往會置于基底上,而基底會影響二維材料的力學性能.尤其是在柔性電子器件和可穿戴設備等情形下,二維材料往往要承受很大的應變[53-55].因此對帶柔性可延展基底的二維材料的面內拉伸性質的研究至關重要.Xiong 等[53-54]通過AFM 納米壓痕實驗和有限元計算分析發現,粘附在PDMS (polydimethylsiloxane) 上的單層石墨烯的彈性模量和斷裂強度和懸空的情形類似,如圖6 所示.PDMS 在石墨烯的保護下,可以抵抗更大的形變.

2.3 原子力顯微鏡在納米壓痕實驗中的測量誤差與來源

原子力顯微鏡在懸空二維材料面內力學性能測量中有獨到的優勢,同時也不可避免地帶來一些測量誤差.目前大多數關于懸空二維材料力學性能的研究都是基于連續介質力學假設:單層二維材料被視為連續的、各向同性的彈性薄膜;并且AFM 探針的尺寸忽略不計,壓力被視為點載荷.然而二維材料的厚度是原子級別的,并且二維材料與AFM 探針之間的范德華作用力不能忽略,因此上述假設并不完全適用于二維材料.Cao 等[56-58]通過molecular mechanics(MM) 模擬發現,當AFM 探針靠近懸空二維材料時,探針與二維材料之間的范德華作用會產生應力與應變的不同步(phase lag),即在真正接觸發生之前(應力依然為零),二維薄膜已產生一個不可忽略的預應變,如圖7(a)所示.因此在實際測量時,針尖的位移和二維材料的中心處的位移并不完全相同.隨著二維薄膜形變的增大,范德華作用的影響迅速減弱,當面內應變>2.5%時,范德華作用可以忽略不計,如圖7(c)所示.此外理論計算發現,二維材料與基底側壁之間的范德華作用力不足以強大到在中心載荷作用下完全固定住二維薄膜.相反的,二維薄膜與基底側壁之間的吸附邊界(adhesive boundary)會在壓力作用下發生剝落,如圖7(b)所示.因此懸空二維材料的納米壓痕實驗更接近于邊界不固定的純彎曲模型,而非大多數實驗工作中使用的邊緣固定薄圓板的彎曲模型[34].Cao 等[34,58]通過理論與計算,發現純彎曲模型給出的應力?應變本構關系與實驗結果更為符合,很好地解釋二維材料納米壓痕實驗中得到的彈性模量普遍偏低的問題.Cao 等[56-57]還對AFM 探針的尺寸對納米壓痕實驗的影響進行了計算,發現只有當懸空二維薄膜的尺寸與壓頭尺寸的比值足夠大于時(>～30),壓頭的尺寸對測量的影響方可忽略不計,如圖7(c)所示.

圖6 石墨烯/PDMS 結構納米壓痕實驗Fig.6 Nano-indentation on graphene/PDMS

圖7 納米壓痕實驗可能誤差來源Fig.7 Possible error analysis of nano-indentation on suspended 2D materials

3 埃壓痕技術和二維材料層間力學性質

基于原子力顯微鏡的納米壓痕技術可以準確地表征二維材料的面內彈性模量E||,而為了完整地描述二維材料的力學性質,范德華作用力對應的層間彈性模量E⊥是不可或缺的.一直以來,研究人員都是利用理論計算或者拉曼光譜等間接手段表征二維材料的層間范德華作用力[59-65],如何精確地直接測量二維材料的E⊥是困擾材料力學領域的一大難題.而為了解決這個難題,美國佐治亞理工學院的科研人員開發了一套同樣是基于原子力顯微鏡的“埃壓痕技術”[29,31,66].顧名思義,埃壓痕技術的壓印形變(indentation depth)在1 nm 以下,對應的形變精度可達到0.1 ?.如此微小的壓印形變與二維材料的層間距十分接近,因此能夠比較準確地“感知”層間的范德華作用力.此外,為了盡可能消除面內的共價鍵對的埃壓痕測量的影響,埃壓痕實驗中的二維材料都需要被放置在一個相對堅硬的基底(例如碳化硅) 上,這樣二維材料的面內形變相對于層間形變可忽略不計,針尖施加的正向壓力基本被范德華作用力所承擔.

3.1 基本原理

埃壓痕技術中的一大難點便是如何精確地控制并且測量二維材料的微弱形變.埃壓痕要求形變在1 nm 以下,由于原子力顯微鏡自身壓電陶瓷的熱漂移以及環境因素的存在,直接進行?級別的位移測量得到的誤差較大.開發者并沒有拘泥于納米壓痕技術的直接測量形變的思路,而是創造性地采用了“間接”測量的方式,即先測量壓力?形變曲線的斜率再對壓力(壓力可通過原子力顯微鏡精確測量)做積分來間接得到壓力?形變曲線.

埃壓痕技術的基本儀器配置如圖8 所示.通過鎖相放大器對原子力顯微鏡的壓電陶瓷在原有的直流信號V0的基礎上施加一個額外的小幅低頻正弦信號?V(ωt),那么此時壓電陶瓷形變則在是直流信號對應的形變z0的基礎上疊加了一個小幅正弦振動?zpiezo(ωt),該小幅振動一般控制在1 ?以下.?zpiezo(ωt) 遠小于z0(4 ～6 nm).在探針十分靠近材料表面時,針尖和材料之間的范德華作用會產生一個“snap in”效應,針尖會被迅速吸附到材料表面.若在進針過程中進行埃壓痕測量,這個吸附力(adhesive force)可以被視為一個額外負壓力,在探針與二維材料未接觸時產生一個預應變,不利于埃壓痕測量.因此埃壓痕測量是在退針過程中進行的.AFM 探針先與被測樣品以30 ～100 nN 的壓力接觸,此時可認為針尖與樣品已完全接觸.此時壓電陶瓷的形變zpiezo

?zpiezo(ωt)對應的正壓力F0的小幅振動?F(ωt)可以被激光探測器接收,但是由于信號過于微弱,一般通過鎖相放大器過濾掉噪音信號.壓力?形變曲線的斜率為

但是此時壓電陶瓷的形變并不等于材料和針尖接觸處的形變,而是等于接觸形變?zindent(或者?zcontact)和懸臂梁彎曲形變?zcantilever的總和

圖8 埃壓痕技術示意圖[66]Fig.8 Schematic of angstrom-indentation[66]

因此可以將接觸處視作一個和懸臂梁串聯的彈簧,彈簧常數分別為kcontact和kcantilever,如圖9(a)所示.將式(7)和式(6)聯立便可得到

式中kcontact便是針尖?材料接觸處形變曲線對應的斜率.我們緩慢地減小正壓力F0并且記錄每個F0對應的kcontact直至針尖與材料表面脫離接觸,再做式(9)中的積分便可得到材料的F?z曲線,如圖9(b)和圖9(c) 所示.值得注意的是,即使經過鎖相放大器過濾,得到的斜率數據依然存在噪音,如圖9(b)所示.對斜率的積分在不失數據有效性的前提下,巧妙地從客觀上對力?位移曲線實現了一次平滑處理,如圖9(c)所示

當針尖與樣品表面分離時,根據接觸力學中適用于變形較小、彈性模量較大情形的Derjaguin-Muller-Toporov(DMT)模型,針尖和樣品之間的吸附力可以被簡單視為一個額外的負壓力Fpull-off (由于是吸引力,Fpull-off 為負)

式中,E?是接觸處等效彈性模量,R是針尖曲率半徑.因此埃壓痕技術通過反向退針測量,將針尖與樣品之間的范德華作用簡單等效成一個額外負壓力.接觸力學中的Johnson-Kendall-Roberts (JKR) 模型相較于DMT 模型,更適用于變形較大、彈性模量較小的情形.在文獻[29,31]中作者對DMT 模型和JKR 模型根據實驗數據做了詳細比較,發現對于石墨烯等二維材料的埃壓痕實驗數據,DMT 模型符合得更好,但兩者差別不大.因此在不失有效性的前提下,一般使用數學形式更為簡潔的DMT 模型即式(10) 對F?z曲線進行擬合,得到等效接觸彈性模量E?

圖9 埃壓痕技術的彈性力學模型Fig.9 Elastic mechanics modelling of Angstrom-indentation

其中E1,ν1和E2,ν2分別是針尖和材料的彈性模量和泊松比.聯立式(9)～式(11)便可得到被測樣品的彈性模量.值得注意的是,埃壓痕技術的目標對象并不限于二維材料,亦可用于表征其他材料的彈性力學性質,例如碳納米管的徑向彈性系數和超硬材料的彈性模量[67-71].

3.2 可能影響埃壓痕測量的因素

埃壓痕技術要求二維材料表面盡可能的平整,褶皺或者其他非常規幾何結構會嚴重影響二維材料力學性能測量[72].例如CVD 石墨烯的褶皺一般在幾納米左右,遠遠大于埃壓痕的壓印形變[73-74],所以對于埃壓痕測量來說,石墨烯相當于是“懸空的”,即便能夠得到低噪音的應力應變曲線,它必然包含了面內和層間彈性模量復合信息,很難從中分離出單純的層間彈性模量相關信息.因此埃壓痕測量時需要盡量避免不平整區域.通常在埃壓痕測量開始之前,會先進行樣品表面形貌的掃描,尋找到一塊平整區域進行測量.由于埃壓痕測量時探針位置保持不動,并且接觸半徑僅僅為幾十納米,所以二維材料在3μm 左右大小的區域內足夠平整即可.

當二維材料層數很少時(例如兩層),埃壓痕測量將不可避免地受到基底的影響.一方面探針施加的壓力會壓縮二維材料與基底之間的距離,使二維材料與基底之間的范德華作用發生變化,增加了受力分析的復雜性.另一方面,即使不考慮二維材料和基底之間的范德華力,施加在二維材料表面的壓力也會使基底發生微小形變.二維材料越厚,以上兩個方面的影響就越弱.理論計算和實驗發現,當形變與二維材料總體厚度的比例小于10%時,基底的作用可忽略不計,具體討論也可見文獻[29]中“semi-analyticalmethods”和“supplementary information”部分.

由于形變很小,因此AFM 針尖的尺寸和形狀對埃壓痕測量的影響十分巨大.接觸力學中的Hertz 模型、DMT 模型和JKR 模型的公式中均包含壓頭曲率半徑,例如式(10).因此在埃壓痕實驗開始前,一般會對AFM 探針進行掃描電子顯微鏡(SEM) 觀測得到探針曲率半徑.亦可對諸如碳化硅、氧化鋅等已知其彈性模量的近似各向同性材料作為基準材料進行埃壓痕測量,利用DMT 模型對力?位移曲線進行擬合得到探針半徑,并和SEM 得到的半徑進行比對.此外,在埃壓痕測量結束之后,也需要對探針進行SEM的觀測:若針尖半徑或者針尖形狀出現明顯變化(例如破損、污染),則該次埃壓痕測量的數據便不可信.

3.3 石墨烯和氧化石墨烯層間彈性模量的直接測量

Gao 等利用埃壓痕技術首次直接測量了碳化硅上生長的外延石墨烯的層間彈性模量,發現其約為33 GPa,與理論預測值十分接近[29].氧化石墨烯(graphene oxide)的反應活性優于石墨烯,可用于制備具有優異力學性能的復合材料[75].Gao 等[29]系統地研究了氧化石墨烯層間彈性模量和層間插層水分子之間的定量關系.層間插層水分子可以顯著的改變氧化石墨烯的層間距,從而改變其電導率、熱導率、摻雜等多種性質.通過控制密閉腔內部的相對濕度,Gao 等[29]實現了層間插層水分子數量的動態控制.埃壓痕實驗表明,氧化石墨烯的層間彈性模量隨著濕度增大從10%濕度下的20 GPa 增大到了25%濕度時的35 GPa,此后濕度的增大反而降低了氧化石墨烯的層間彈性模量,最終在50%左右的濕度時層間彈性模量回落到了最初的20 GPa 左右.該現象的可能機理為:在低濕度時,層間插層水分子增加了氧化石墨烯的層間距從而減弱了范德華吸引力,同時水分子亦會減弱氧化石墨烯之間的接觸,因此此時層間彈性模量低于石墨烯的層間彈性模量.隨著濕度的增大,插層水分子逐漸填滿了氧化石墨烯的層間空間,并且形成一層氫鍵網絡,水分子層可被視為“額外”的一層氧化石墨烯,反過來加強了氧化石墨烯系統的層間范德華作用力,此時層間彈性模量會增大到和石墨烯接近的35 GPa.隨著水分子數量持續增大,第二層水分子開始形成,層間距再次擴大,同時在水分子流動性的作用下,層間彈性模量開始降低.具體的數據展示在圖10 中.

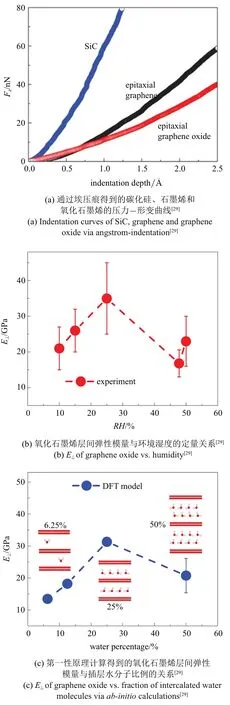
圖10 氧化石墨烯的層間力學性質Fig.10 Out-of-plane elasticity of graphene oxide

3.4 雙層石墨烯?單層金剛石相變

石墨和金剛石是自然界中最常見的碳的同素異形體.通過對石墨施加高溫高壓的是工業上常用的人工合成金剛石的手段.自從石墨烯被發現之后,科研人員一直致力于合成超薄甚至單層的金剛石的結構[76-79].Gao 等[80-81]發現在常溫下利用原子力顯微鏡施加10 GPa 左右的局域壓強可以驅使碳化硅上的雙層外延石墨烯轉化為單層金剛石結構,如圖11(a) 所示.他們同時利用原位埃壓痕技術直接測量了單層金剛石結構的彈性模量,發現其約為1 TPa,與天然塊體金剛石接近.埃壓痕測量的結果如圖11(b) 所示.硬度測量從側面佐證了相變的發生:在同等壓力下,多層石墨烯和碳化硅都發生了塑性形變,而雙層石墨烯則完好如初,如圖12 所示[80].該工作充分地展現了原子力顯微鏡和埃壓痕技術的強大功能.

圖11 雙層石墨烯?單層金剛石相變Fig.11 Bilayer graphene–monolayer diamond phase transition

圖12 單層金剛石、碳化硅、多層石墨烯的硬度測量[80]Fig.12 Hardness of monolayer diamond,SiC and multilayer graphene[80]

4 范德華異質結

當將幾種不同的二維材料垂直堆疊起來時,由于層間范德華作用力,可形成許多新奇的異質結構[82-87].范德華異質結“任意搭配”的特性可以把這些單獨的二維材料像樂高積木一樣結合到一起,如圖13(a) 所示,在仍保持超薄的厚度的基礎上呈現出令人驚奇的物理性質.例如把雙層石墨烯輕微旋轉約1.1?(所謂的“魔角(magic angle)”),狄拉克點附近電子能帶變得十分扁平,雜化的層間電子在狄拉克點的費米速度趨近于零,電子有效質量急劇增大[88];并且當導帶或者價帶處于半滿(half-filling)狀態時,本應呈現金屬特性的“魔角”石墨烯卻表現出反常的莫特絕緣體性質;如果使費米能級稍微偏離半滿態,“魔角”石墨烯甚至能變成超導體[89].然而目前大多數關于范德華異質結的研究聚焦于其電學和光學性質,對其潛在的可能奇異的力學性質的研究則有所欠缺.Liu 等[43]發現MoS2/WS2雙層異質結構的二維彈性模量低于其單體結構二維彈性模量的總和,但與相應的雙層單一材料結構相似,如圖13(b)所示.范德華異質結之所以不同于普通單體二維材料,其根源便在于二維材料的層間范德華耦合,因此精確表征和調控層間作用力對范德華異質結的基礎認知和未來應用有著十分重大的意義.由于埃壓痕技術的獨特的施加?級形變的能力,可能是范德華異質結層間力學性質測量難題的可行的解決方案.例如用于研究不同材料、不同層數、不同角度組成的范德華異質結材料的等效層間彈性模量;也可利用埃壓痕技術施加微小形變,同時進行原位電輸運測量,研究范德華作用力對電子學性質的影響.

圖13 范德華異質結示意圖及其力學性質Fig.13 Schematic of van der Waals heterostructures and their elastic properties

5 總結與展望

原子力顯微鏡能夠在納米甚至埃尺度上施加壓力和測量形變,在二維材料及其異質結構的彈性力學性質的研究方面展示了強大的功能,是目前最常用的納米材料力學性質的研究手段.基于原子力顯微鏡的納米壓痕技術可用于表征無支撐二維材料及其異質結構的面內力學性質.而同樣基于原子力顯微鏡的埃壓痕技術在垂直表面形變的精度上比納米壓痕技術提高了一個數量級,達到了埃級別,完美適用于測量范德華材料的層間力學性質,很好地填補了納米壓痕技術在這方面的不足.

隨著前沿科學和新技術的不斷發展,對工程材料與結構的超常規尺度、硬度、剛度等極端性能以及在超常規壓強等極端服役環境中的力學響應規律的研究,既是力學發展和研究的需要,更是與關乎國計民生的重大科研與工程項目密切相關[20].新型材料在微納尺度上展現出的極端性能和在超高壓強等極端外界條件的力學性能,也許是實現其在重大工程(例如航空航天、關鍵裝備等)和民用(例如可穿戴柔性設備) 等領域具體應用的一個可能的突破口[90].因此對于二維材料力學性能的研究,無論在力學基礎研究領域還是工程應用領域都有重大意義,基于原子力顯微鏡的力學測量手段在未來無疑將發揮更大的作用.