以模型為例 探究幾何最值問題

張海霞

摘 要： 在初中數學中，常常遇見求解幾何最值的問題，由于這類題型的綜合性強，形式靈活多變，知識點涉及廣泛，學生常常束手無策.想要掌握這類題目并不難，需要學生把握好常見的類型，透過現象看本質，深度挖掘題目背后的知識點，再結合相關知識來進行轉化，就可以化繁為簡了.本文就初中數學幾何最值問題的探究做出詳細的思路分析，并且提出相關的學習建議.

關鍵詞： 初中數學;幾何最值;模型;合理轉化

中圖分類號： G632?????? 文獻標識碼： A?????? 文章編號： 1008-0333（2021）35-0034-02

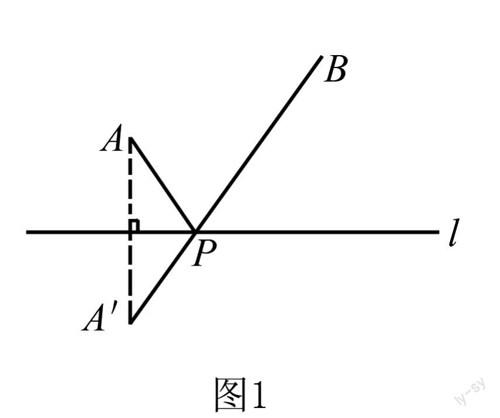
一、“將軍飲馬”模型解讀 幾何最值問題的形式靈活多變，但是它之間蘊含的基本模型是一定的，模型如下：

模型滿足的條件：如圖1所示，有一條已知直線l和直線外兩點A、B，并且點A、B在直線l的同一側，點P為一個動點，它只能在直線l上運動.

根據模型提出問題：如果要使得PA+PB的值最小，那么，動點點P應該處在直線l的哪一處？

解析? 作出所需的輔助線，作點A關于直線l的對稱點，設為點A1，然后連接線段A1B，并且線段A1B與直線l相交產生交點，此交點為了符合題意時點P的位置，那么，PA+PB=A1P+PB=A1B.

方法解讀? 因為在作輔助線時，首先找的是點A關于直線l的對稱點，點P在直線l上運動，所以不管點P在直線l上的哪一點，根據軸對稱的特性可以知道：PA=A1P，這時這個題目就被轉化為求A1P+PB的最小值，又因為求的是三個點之間的所連線段的最小值，因此，可以根據原理：“兩點之間線段最短”，將三點化為兩點，即當點A1、P、B共線時，A1P+PB可以取得最小值，從而實現了線段的“化”“折”“為”“直”.

二、問題探究

類型? 幾何圖形中的線段與最值

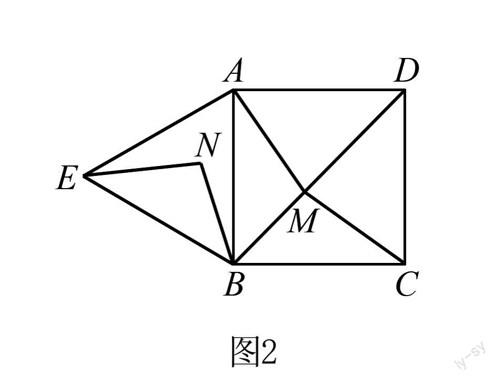
例1? 如圖2所示，此圖由一個正方形ABCD和一個等邊三角形ABE所組成，并且已知在正方形ABCD的對角線BD上有一個動點M，點M不與點B重合，如若將線段BM以點B 為旋轉中心，逆時針旋轉60°，這時點B落在了點N處，最后將CM、AM和EN連接起來，請根據以上條件回答問題.

（1）試證明：ΔAMBΔENB.

（2）①如要使得AM+CM有最小值，那么，點M應該在線段BD的哪一處;

②如果要使得AM+BM+CM有最小值，那么，這時點M又該位于和位置呢，請說明理由.

解析? 對于第一小問，本小題比較簡單，只需要根據正方形和等邊三角形的性質，找到兩個需要證明全等的三角形對應邊相等即可，過程略.

第二小問，①這道題目和例題“將軍飲馬”很相似，解題方法是一樣的，其中涉及三個點，由于兩點之間線段最短，可以得出線段AC與線段BD的交點為點M時，就是題目所求的最小值的情況，那么，此時點M為BD的中點.

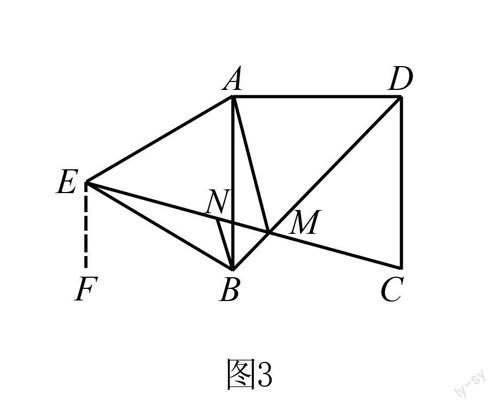
②求解線段和的最小值，我們需要采用等線段轉化的方法，如圖3所示，首先作出所需輔助線，連接CE、MN，然后過點E作CB延長線上的垂線，設垂足為點F，在這里我們需要利用第一小問的結論即△AMB△ENB，∴AM=EN，∠MBN=60°，MB=NB，∴△BMN為等邊三角形，∴BM=MN，那么，AM+BM+CM=EN+MN+CM.

又兩點之間線段最短，可知當點E、N、M、C共線時，有EN+MN+CM=EC，

綜上所述，當點M為EC和BD的交點時距離最短.

解析? 這道例題是幾何圖形的線段和最值問題，涉及三線、四點，但是不管怎樣，解題的原理還是一樣的，碰到需要化“折”為“直”的問題時，可以采用軸對稱來進行變換，還可以利用“兩點之間線段最短”的原理來確定最值的情況.

三、幾何圖形的周長最值問題

例2? 如圖4所示，在四邊形ABCD之中有兩個直角，分別為∠B和∠D，并且∠C=50°，已知點E位于線段BC上，點F位于線段DC上，試求當△AEF的周長取得最小值時，∠EAF的度數是多少？

解析? 本道例題求解周長的最值問題，我們可以先確定ΔAEF周長最小時的情況，再來求∠EAF的度數，L△AEF=AE+AF+EF，需要根據基本的模型來進行轉化才可以解出題目.

如圖5，過點A作出關于BC的對稱點M，再過點A作關于CD對稱的點N，然后將MN連接起來，設線段MN與線段BC的交點為E，線段MN與線段CD的交點為F，那么在這時點M、E、F、N四點共線，AE+AF+EF=EM+NF+EF=MN，ΔAEF的周長是最小的.

由軸對稱的特性可以知道，∠M=∠BAE，∠N=∠DAF，

又∵∠BAD=130°，并且∠M+∠N=50°，

∴∠BAE+∠DAF=50°，

∴∠EAF=130°-50°=80°.

本題屬于幾何圖形周長的最值問題，需要結合周長公式將求解幾何圖形的最值問題轉化為求解線段和的最值問題，此類題型的特點就在于它涉及到的線段和關鍵點更多，雖然難度增加了，但是只要掌握了原理，在實際分析時進行多次軸對稱變換，這類題目就會迎刃而解.

通過上述幾道例題的解析與思路分析，我們不難發現這類題型的關鍵點在于掌握“兩點之間線段最短”原理，并根據原理進行多次轉換就可以簡化題目，根據軸對稱的特性，做到化“折”為“直”，再結合“兩點之間線段最短”找出動點滿足題意的位置，當涉及三線、四點時，更應該找到線段相等的線段，將其替換，然后找到它們的交點，一般這個交點就是我們所求的點.不難發現，這類題型涉及的知識點還是挺多的，比如“兩點之間線段最短”“垂線段最短”以及“線段平移”，還有軸對稱的特性，因此，在平時就要求學生對這些基礎知識點非常熟悉，并且需要掌握一些基礎的問題模型，研究透這些模型，夯實基礎，勤加練習才是最重要的.

參考文獻：

[1]汪仁林，朱養鋒.例析與圓有關的最值問題[J].中學生數學，2014（03）：4-5.

[2]楊路.這類幾何最值問題有意思[J].數理天地（初中版），2021（05）：22-23.

[3]楊路.例談幾何最值問題的破解思考[J].數理化學習（初中版），2020（10）：16-18.

[責任編輯：李 璟]