不規則井眼固井環空流動壓降變化規律

鄭雙進，劉濤，廖坤，李足平，杜冬楠，劉裕，潘祎

1.長江大學石油工程學院，湖北 武漢 430100 2.中石化勝利石油工程有限公司固井技術服務中心，山東 東營 257100

固井環空壓力剖面的精確計算與控制非常重要，尤其是針對密度窗口較窄的地層，壓力控制不好容易發生井漏或溢流等事故，影響施工安全和固井質量。由于地層縱向非均質性的影響，或存在嚴重鹽膏層、泥巖段，井眼垮塌嚴重，井徑擴大率不均勻形成“大肚子”不規則井眼十分常見[1]。據統計，全球泥頁巖地層占75%，90%的井眼穩定性問題發生在泥頁巖，有的層段擴徑，有的層段縮徑，很容易形成“大肚子”或“糖葫蘆”不規則井眼[2]。從公開文獻報道也可同樣得知，國內各大油田也普遍存在不規則井眼油氣井[3]。不規則井眼固井過程中易發生油、氣、水竄問題，影響界面膠結質量，進而影響固井質量[4-8]。據調研，早在1986年FRANK等[9]就針對突擴流進行研究，得到了級聯展開的納維葉-斯托克斯解；王常斌等[10]建立了突擴管在低雷諾數條件下的物理模型，采用正交網格劃分，對牛頓流體層流下的管路突擴情況進行了數值模擬，分析了管路突擴回流時速度和壓力的流場的分布情況；朱曉星等[11]基于非均勻網格Lattice-Boltzmann方法對二維突擴流進行了數值模擬，并驗證了該方法的適用性；劉曉利等[12]運用有限分析法求解Navier-Stokes方程，獲得了二維突擴管流的數值解；夏慶福等[13]應用標準k-ε雙方程模型對洞塞消能進行了數值模擬計算，與經驗公式計算結果相比誤差小于5%。前述研究均是針對突擴流進行的，而實際不規則井眼大多為井壁曲線呈弧線狀的弧形凹面井眼，與突擴管形態存在一定差異，目前鮮有描述弧形凹面區域流場規律的理論模型相關報道，該區域的流動壓降情況也無從得知。因此，建立一套能夠描述弧形凹面區域流動壓降的計算方法，分析弧形凹面區域的流動壓降變化規律及影響因素，對于精細計算不規則井眼環空壓力剖面十分重要。

1 不規則井眼流動壓降分析

如圖1所示，當固井流體從小直徑環空進入大直徑環空時，小直徑環空中的流線可近似看作平行直線，井徑變化區域會產生旋渦；當固井流體從大直徑環空進入小直徑環空時，流線收縮，井徑變化區域也會產生旋渦[14]。以上2個過程的流動求解復雜，這里為簡化求解，將流動區域劃分為環形流動區域與弧形凹面流動區域。 相應地，整個流動區域內的壓降為環形流動壓降與弧形凹面流動壓降之和。對于環形流動區域，使用Burkhart給出的冪律流體環空壓降計算公式求解固井流體在該區域的流動壓降[15]。對于弧形凹面流動區域，運用平板驅動流理論描述其流動問題，以下通過推導弧形凹面區域的能量方程來分析該區域的附加壓降。

圖1 弧形凹面井眼固井流體流動示意圖 圖2 微元控制體示意圖 Fig.1 Schematic diagram of cementing fluid flow in the Fig.2 Schematic diagram of the element control body borehole with curved concave surface

如圖2所示，弧形凹面流動區域任一微元控制體內能量守恒定律為體積τ內流體動能和內能的變化率等于單位時間內質量力和面積力所做功加上單位時間內給予體積τ的熱量，則弧形凹面流動區域內的能量守恒定律可表達為：

(1)

式中:τ為微元體體積；S為微元體表面積；T為溫度的微分；ρ為流體密度；Q為微元體內能；t為時間；v為速度矢量；n為微元面外法線方向單位矢量；F為體積力矢量；k為導熱系數；q為熱量；P為二階張量，包含正應力與切應力。

全微分形式的能量變化率可轉化為如下偏微分形式：

(2)

式中:vn為垂直于微元表面的速度。

根據奧高公式將面積分轉化為體積分：

(3)

(4)

此時積分形式的能量守恒方程可轉化為：

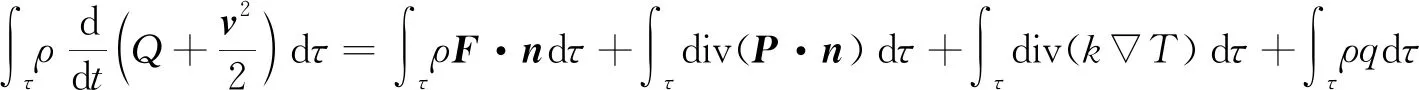
(5)

由于微元τ是任意的，且假定被積函數連續，由此可導出：

(6)

假定在流動過程中沒有熱量交換，即:

則有：

(7)

兩邊同時對時間t積分可得：

(8)

在t=0時刻，v=0，則有：

(9)

除了平板驅動切應力及正應力外，其余的正應力與切應力均為內力，整個弧形凹面流動區域內力所做功總和為0。另外，考慮到壁面無滑移邊界條件，說明壁面并不對流體做功，故只有重力及驅動剪切力對流體做功，所做功即為整個弧形凹面流動區域的動能。

在圖2中的環形流動區域與弧形凹面流動區域接觸面處功能關系為：

(10)

式中：S0為環形流動區域截面積。

當|v|dt=L時，弧形凹面區域的附加壓耗：

(11)

2 弧形凹面區域流動控制方程

2.1 連續性方程

在固井流體中取由一定流體質點組成的物質體，根據質量守恒定律，并假定固井流體是不可壓縮流體，廣義坐標系下的連續性方程可表示為：

(12)

考慮徑向對稱性，則柱坐標系下的連續性方程為：

(13)

式中:vr為徑向速度；vz為軸向速度。

2.2 動量守恒方程

廣義坐標系下的動量守恒方程可表示為：

(14)

考慮徑向的對稱性后，動量守恒方程在柱坐標系下表示為：

(15)

2.3 柱坐標下控制方程的無量綱化

取流場的特征長度、特征速度、特征時間、特征壓力，將控制方程無量綱化：

(16)

無量綱化后的方程統一為：

(17)

式中：Re為雷諾數；X、Y分別為x與y方向特征化后長度；U、V分別為x與y方向特征化后速度；p為特征化后壓力。

將控制方程無量綱化以后，可以避免控制方程中物理參數在量級上的懸殊差異，從而減少不必要的數值誤差和精度損失，同時可減少控制方程中的常數運算而將常數轉化成幾個相似參數；此外，還易于實現數值計算中的相似模擬，從而使計算結果更具通用性。

3 弧形凹面區域流場求解

3.1 控制方程的離散

對于驅動流問題，目前最常用的解法是交錯網格法。所謂交錯網格就是把速度U、V及壓力p(包括其他所有標量場及物性參數)分別存儲于3套不同網格上的網格系統中。其中速度U存在于壓力控制容積的東、西界面上，速度V存在于壓力控制容積的南、北界面上，U與V各自的控制容積是以速度所在位置為中心，求解過程中所建立的交錯網格如圖3所示。偏微分控制方程組采用有限差分進行離散，對速度項采用顯式格式，對壓力梯度項采用隱式格式，空間所有導數項均采用中心差分格式，時間步長為Δt，空間步長為ΔX與ΔY。

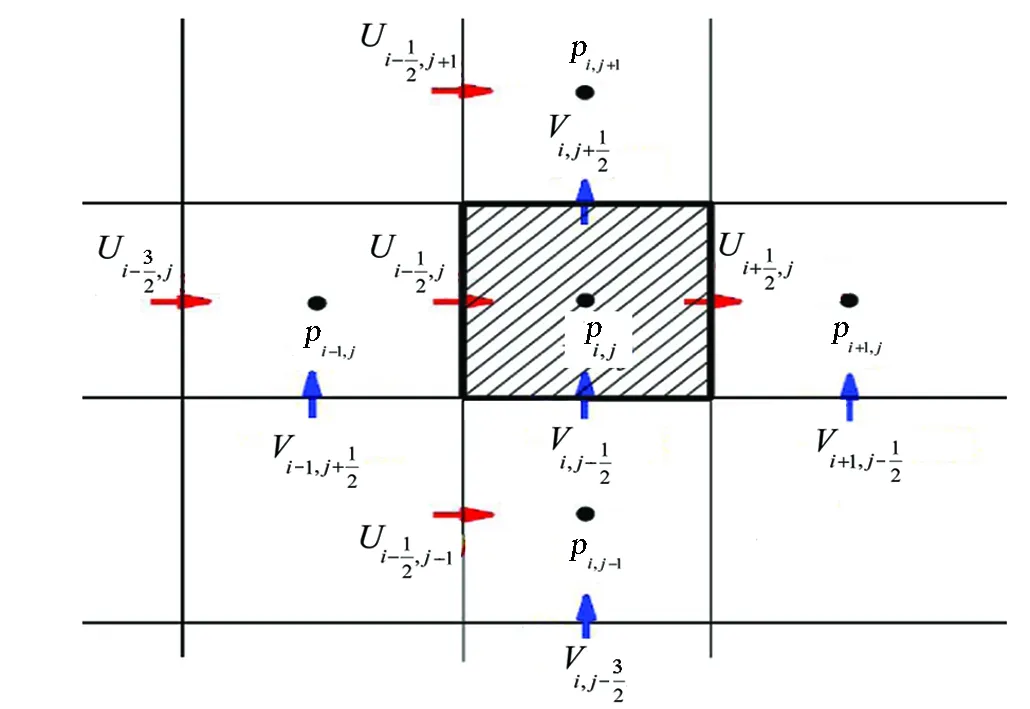
圖3 交錯網格示意圖 Fig.3 Schematic diagram of staggered grid

將離散后的動量方程代入離散后的連續性方程中得：

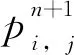
(18)

3.2 求解流程

1)定義變量，賦初始值、邊界值與參數值，如Re；

2)確定網格信息，如空間步長、時間步長：ΔX，ΔY，Δτ；

4)將離散動量方程代入離散連續方程構造統一的壓力方程；

5)以中間速度為源項求解壓力方程，采用迭代法直至收斂；

7)令t=t+Δt，返回步驟3)，以最新值進行下一步推進，直至推進到穩態為止；

8)有且需求穩態值時一直推進到穩態為止，無或不求穩態值時推進到一定時刻終止。

4 實例應用

4.1 實例計算

基于上述建立的理論模型和求解方法，運用VB6.0程序設計語言開發了弧形凹面井眼流動計算分析軟件，可計算弧形凹面井眼段的流體流動壓降變化規律，并分析井徑擴大率和流體排量對流動壓降的影響規律。

南海某井固井前實測井徑曲線如圖4所示，合理簡化設置模型總長1m，弧形凹面井眼段長0.5m，上下兩端的規則井眼段各長0.25m，鉆頭直徑444.5mm，套管外徑339.7mm；弧形凹面井眼剖面線為正弦曲線，流經弧形凹面井眼段的固井流體密度為1.8g/cm3，流性指數n為0.82，稠度系數k為0.53Pa·sn，黏度為40mPa·s。為了對比分析不同井徑擴大率和不同排量條件下的流動壓降，井徑擴大率依次為0、20%、30%、40%、50%、60%，流體排量依次取30、40、50L/s，計算結果如圖5所示。

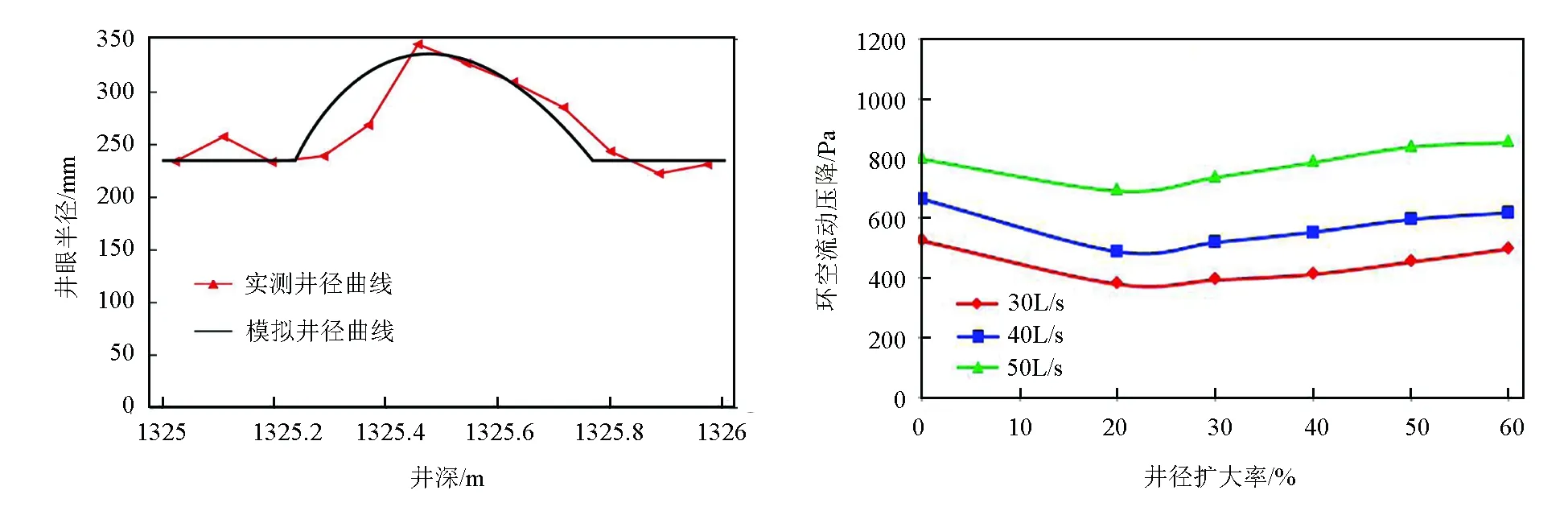
圖4 南海某井固井前實測井徑曲線 圖5 不同流體排量下的流動壓降計算結果 Fig.4 Measured diameter curve of a well in the South Fig.5 Calculation results of flow pressure drop at China Sea before cementing different fluid displacements

4.2 數值模擬

采用Fluent軟件進行數值模擬驗證。由于井下弧形凹面井眼段的入口壓力及出口壓力未知，故在進行數值模擬時采取入口流量條件，出口壓力條件(壓力為0)。其網格劃分情況(以井徑擴大率50%為例)如圖6所示，排量分別為30L/s與50L/s時模擬結果如圖7所示。

圖6 弧形凹面井眼段流動數值模擬網格劃分圖Fig.6 Numerical simulation results of flow pressure drop under different fluid displacements

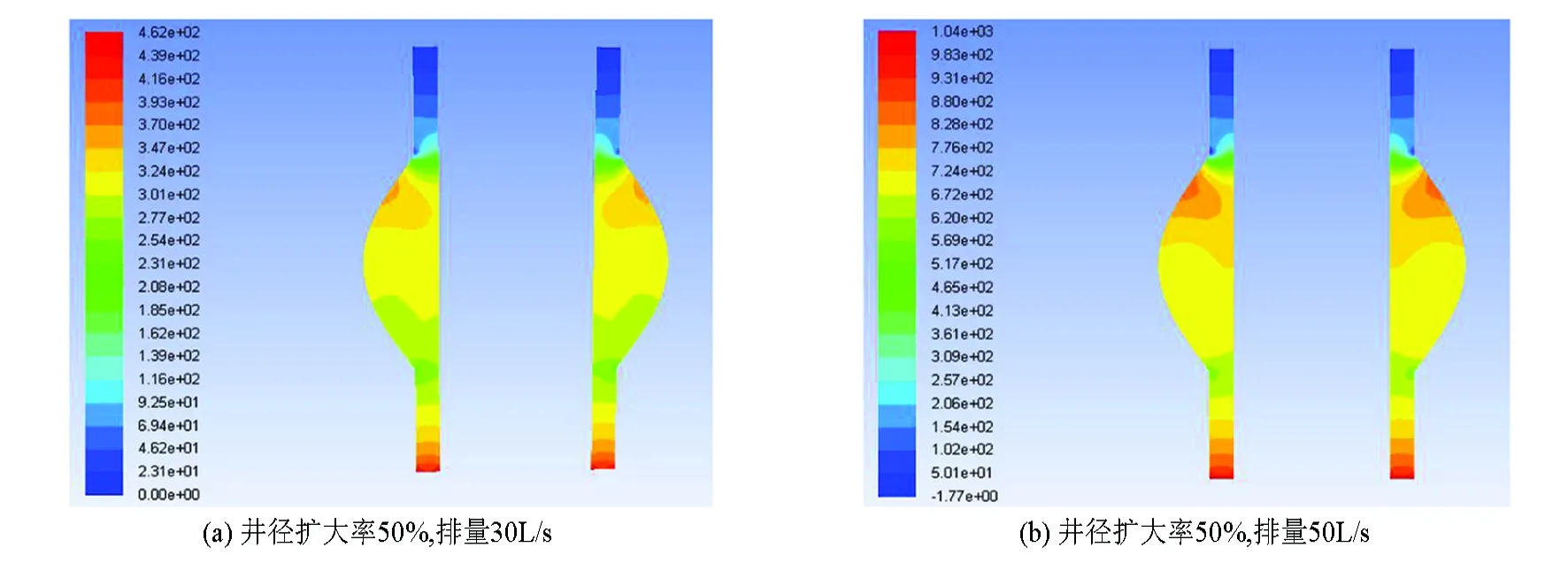
圖7 弧形凹面井眼段壓力場圖Fig.7 Pressure field diagram of the borehole with curved concave surface

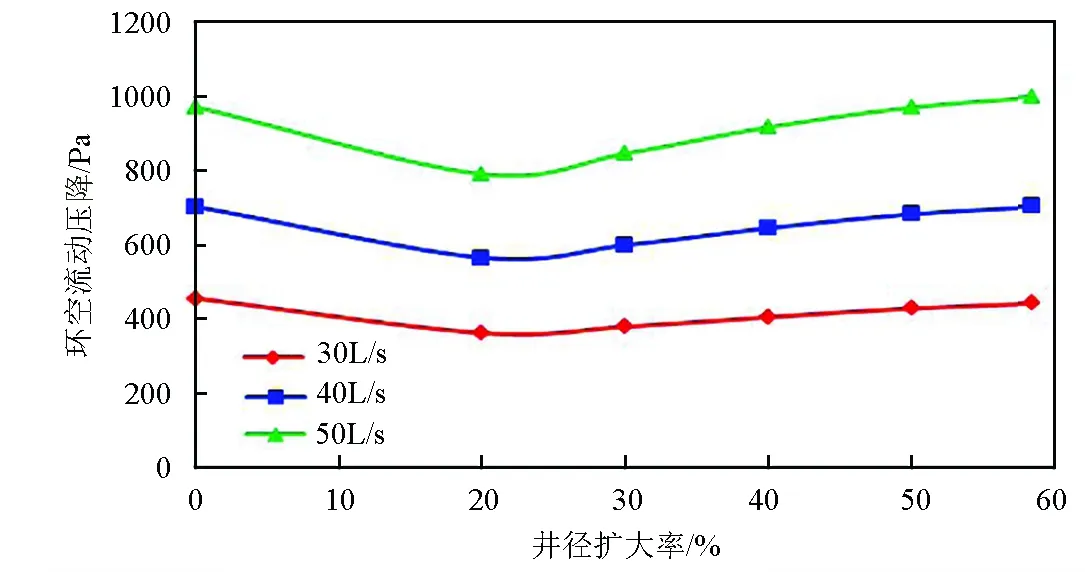
圖8 不同流體排量下的流動壓降數值模擬計算結果 Fig.8 Numerical simulation results of flow pressure drop under different fluid displacements

依據數值模擬結果，繪制弧形凹面井眼流動壓降隨井徑擴大率變化數值模擬曲線，如圖8所示。

從圖5和圖8可以看出，在同等井徑擴大率條件下，排量越大流動壓降越大；在同等排量條件下，隨著井徑擴大率的增大，流動壓降呈先減小后增大的趨勢；在常見的井眼擴徑范圍內，弧形凹面井眼的流動壓降小于正常井眼的流動壓降。對比圖5和圖8，軟件計算和數值模擬分析結果大體一致，且趨勢相同，數據偏差分析如表1所示。

從表1可以看出，軟件計算結果和數值模擬分析結果偏差均在15%以內。由于環空壓降在井筒壓力中所占的比重較小，因此該數據偏差在工程計算允許的誤差范圍內，由此可認為筆者所建立的模型能夠描述弧形凹面區域的流動問題，對于固井環空壓力的精細計算具有一定的參考價值和指導意義。

表1 軟件計算結果與數據模擬計算結果偏差分析

5 結論

1)通過建立弧形凹面井眼條件下的流動壓降方程,分析了壓降的構成，建立了環空流體控制方程，研究確定了求解方法與流程，并開發軟件進行了計算分析，運用Fluent數值模擬軟件進行了驗證，軟件計算結果與數值模擬結果偏差在工程允許的誤差范圍內，為固井環空壓力的準確計算與控制提供了參考。

2)軟件計算與數值模擬結果表明在同等井徑擴大率條件下，流動排量越大，弧形凹面井眼段的流動壓降越大；在常見的井眼擴徑范圍內，弧形凹面井眼的流動壓降小于正常井眼的流動壓降。