基于多態分量與3D卷積相融合的帶寬預測方法

段 浩，趙 璞，鄭思源，張清周，季 節，吳昌設，張晉陽

（1.國網浙江省電力有限公司溫州供電公司，浙江 溫州 325000；2.華北電力大學，北京 102206）

0 引言

2019 年，國家電網有限公司基于能源互聯網的特點功能和企業的責任使命，提出了“三型兩網”的發展戰略，作為“三型兩網”中“兩網”的智能電網正逐漸成為電力網研究的熱點。“兩網”融合之后必將使現有的電網需求體系產生全新的變化，能盡快適應變化，提前預知要求，提出解決方案，才能更好地促進“兩網”融合。日益增長的用電需求和對電能質量的需求，非線性化、多樣化的負荷特點，規范化配置、區塊化分布、微網組合成網等未來的配電網新形態，這些電力需求給配套通信體系中的負荷預測帶來了更大的挑戰，對負荷預測的可靠性與有效性都提出了全新的標準。

在智能電網領域，當前配用電通信網帶寬計算研究主要集中在彈性系數帶寬計算方法。本文針對目前帶寬預測方法存在的帶寬利用率不高、僅針對預測當地進行研究而忽視相鄰地區的影響等問題，提出了一種基于3D 卷積和最小二乘法的動態、靜態分量的通信帶寬估算方法，在滿足傳輸安全可靠性的前提下，優化帶寬資源分配。

1 區域用地網格化與網格內帶寬空間分布

空間負荷預測定義為：在把規劃區按照一定的原則劃分成一定數目的小區的基礎上，通過分析，預測各個小區在規劃年的負荷密度或土地利用情況，從而進一步預測整個規劃區在規劃年的負荷分布位置和數量。在電力系統領域，網格的劃分一般是依據供電區域的行政級別或供電區域規劃水平年的負荷密度。在電力通信領域，可以借鑒這些考慮因素，但省與省之間的經濟、用電水平和帶寬需求水平并不相同，因此必須找到一種全面的方式進行網格細分，使得對未來帶寬的規劃更加合理。本文將供電網格作為帶寬預測的基本單元，網格的劃分應遵循以下原則：

（1）經濟發展水平和用地屬性相同或相近。

（2）開發深度和用電需求相同或相近。

（3）地理位置和周邊環境相同或相近。

（4）邊界基本與道路走向一致，依照功能區劃分。

（5）面積以0.01～5 km2為宜，面積過小的區塊歸入鄰近網格，面積過大的網格應進一步細分[1]。

2 基于3D 卷積的網格帶寬預測算法

2.1 3D 卷積神經網絡基本原理

每個卷積層由若干個卷積核組成，卷積核的數量決定了通道數。3D 卷積公式如下：

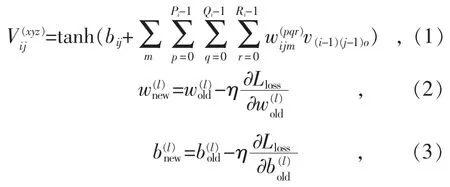
池化是卷積神經網絡中另外一個及其重要的概念，它實際上是一種形式上的降采樣，目前應用最為廣泛的是“最大池化”，即對每個子區域輸出最大值，“平均池化”則是輸出每個子區域的平均值。池化可以減小數據的空間，降低參數的數量和計算量，從而在一定程度上控制過擬合[4-5]。

損失函數又稱代價函數，用來評價現有模型對已有樣本預測結果的好壞，常見的損失函數有交叉熵損失函數、指數損失函數、鉸鏈損失函數。在訓練卷積神經網絡時，通過不斷最小化損失函數，優化卷積層和全連接層的權重和偏置，從而使網絡達到最優狀態。為避免過擬合，本文采用L2 正則化方法[6-7]。

2.2 數據空間處理

2.2.1 靜態分量計算

設某網格內帶寬時間序列X={x1，x2，…，xM}，對X 進行差分計算得到矩陣A：

式中：f 與n 為設置的參數，f－1 為周期能取到的最大值，在實例中應使f 盡可能大。對矩陣A 的每一行進行線性擬合，f－1 行每一行線性擬合后的參數分別記為（a1，a2，…，af－1），（b1，b2，…，bf－1），得到對應的A1，即：

計算A 與A1每行最小誤差和列矩陣E，其中首次出現最小誤差的行數即為活動周期L。誤差矩陣E 的計算公式為：

其中，

將時間序列X 以周期L 進行劃分，得到矩陣B：

式中：xM為時間序列X 的最后一個數據，之后的數據均為空值NA。根據周期內前N 個點預測第N+1 個點的靜態分量，若N 為0，則根據前一個周期的L 個點預測本周期第一個點的數值。將矩陣B 同一周期行內的各個歷史數據進行擬合，每個擬合線間是首尾連續的。采用最小二乘法多項式對序列靜態分量進行擬合，將所有周期內初始數據作為訓練樣本進行建模，建立靜態分量預測模型Sij（t），i 與j 表示網格所處的位置：

式中：Sij（t）為時刻t 的靜態分量；b0至bk為時刻t 的靜態分量Sij（t）的擬合參數，k 為最小二乘法多項式值。對于t 取任意值時此周期內都有一個序列點，則所有周期內所有點到此擬合直線的距離平方R2為：

不斷優化參數，使得R2值最小，此時表示擬合函數與真實值誤差最小，對應的多項式參數即為最終擬合函數參數，得到最終的靜態分量預測模型Sij（t），通過Sij（t）預測各個網格時刻t 的靜態分量。

2.2.2 動態分量計算

本節應用3D 卷積方法得到網格的動態分量。與常見的3D 卷積方法相比，本文將3D 卷積與最小二乘法相結合，先將最小二乘法得到的預測結果作為帶寬的靜態分量，在一定程度上表示該預測網格的固定帶寬需求；但動態帶寬需求（如移動端的帶寬）預測不僅與網格內部發展程度有關，還與預測網格周邊網格的分布情況有關，且城市規劃網格內的總動態帶寬分量有上限，總量在短期內不會有較大波動，波動主要體現在動態分量在各個相鄰網格間的移動上。因此，采用最小二乘法得到的周期L 構造動態數據集，并以L 為參考量搭建3D 卷積神經網絡，進而訓練3D卷積神經網絡，獲取動態分量。

從時空角度觀察所有網格帶寬數據時，數據常以固定的時間間隔和空間的固定位置記錄，如圖1 所示。

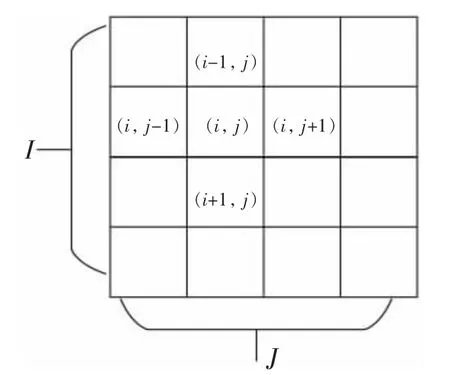
圖1 時空角度觀察網格數據

在某一時刻t，所有網格的數據用S=Sij（t）表示，當t 固定時，Sij（t）為一個視頻幀，每個像素點上數據為該網格的帶寬數據，將Sij（t）的差分序列作為動態通信數據庫：

3D 卷積相比于2D 卷積能夠更大程度地捕捉數據的空間特征和時間特征。基于感受野理論，不同尺寸的卷積核能夠得到不同類型的特征，從而最大程度地避免由于單一卷積核帶來的特征提取不完整對預測結果的影響。

設預測時刻t0的動態分量，構建動態數據集U：

2.3 結合多態分量的網格帶寬預測

將靜態分量Sij（t）與動態分量Dij（t）相結合，對于每個網格，將其對應的靜態分量與動態分量相加，得到網格在時刻t0的總流量Wij（t）：

各個網格的流量累加即得到該地區的總流量W（t），并通過W（t）與預測用地總面積S 得到信息流量密度ρ：

3 算例分析

3.1 數據集

以鎮江部分地區的通信帶寬數據為原始數據，根據前文的網格劃分方法，取3×3 的網格作為本實驗數據，采用2.2 節的方法，取m=16，n=32，得到可以實驗的數據。并在求得網格周期分量L 后，通過差分的方式構建動態數據集U[8-9]。

3.2 靜態分量與網格周期求解

對每個網格內的數據進行2.2.1 節的處理，得到9 個誤差矩陣（見圖2），首次出現最小值的行數為該網格的網格周期L，因該值體現了網格內部數據循環趨勢，故取該值作為動態數據集的周期求得各個網格的靜態分量見圖3。

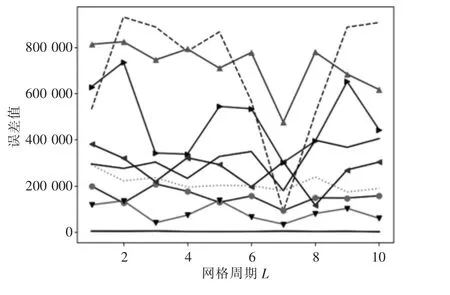
圖2 誤差矩陣

圖3 靜態分量

3.3 神經網絡模型構架與動態分量

先將動態數據集U 的數據進行歸一化處理，方便神經網絡進行優化，同時為了應對數據較少所導致的過擬合現象，本文在神經網絡末端采用L2 正則化方法，代價函數為：

式中：θ 為卷積核權值；hθ（x（i））為假設函數的輸出；x（i）為假設函數的輸入；y（i）為與其對應的標簽；λ 為正則化系數；θj為第j 個卷積核權 值；Nepoch為神經網絡訓練的次數；Nnum為所有權重的個數。

6 種3D 卷積神經網絡模型參數如表1 所示。6 種網絡模型交叉熵結果如表2 所示。通過比較不同模型下的交叉熵結果，選定2 號神經網絡作為本文實驗網絡。

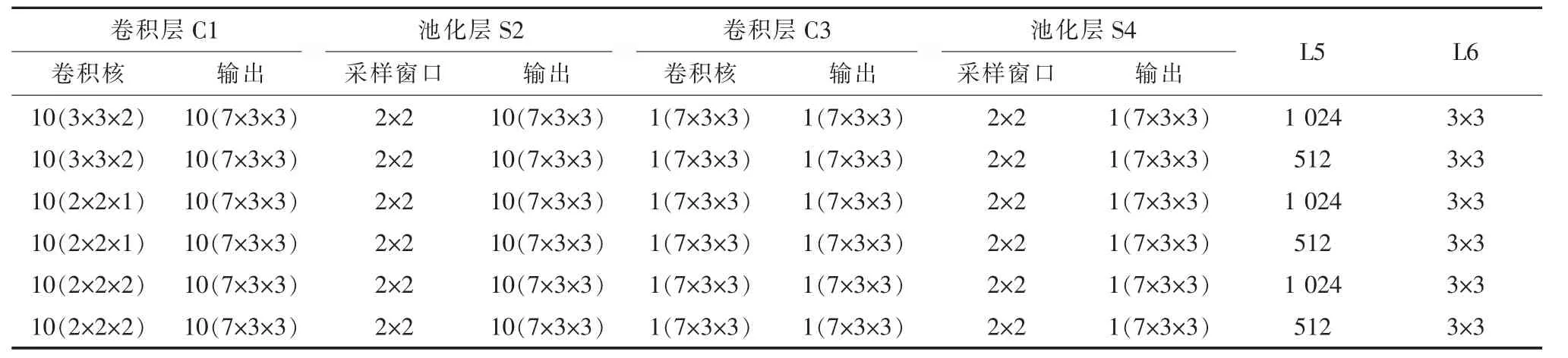
表1 3D 神經網絡模型參數

表2 6 種網絡模型結果對比

3.4 實驗結果與分析

采用2.3 節的方法對各網格帶寬進行預測，并將本文預測結果與彈性系數法結果、實際數據進行對比，如圖4 所示。

圖4 實驗結果

采用預測領域常見的3 種度量指標來衡量預測精度，包括MAE（平均絕對誤差）、MAPE（平均絕對百分比誤差）和RMSE（均方根誤差）[10-12]：

式中：εMAE，εMAPE，εRMSE分別為MAE，MAPE，RMSE的值；h（xi）為預測值；yi為實際值；C 為預測網格的個數。不同預測算法的精度比較見表3。

表3 不同預測算法的精度比較

彈性系數是一定時期內相互聯系的兩個經濟指標增長速度的比率[13]，它是衡量一個經濟變量的增長幅度與另一個經濟變量增長幅度的依存關系。從計算方法上看，彈性系數又有名義彈性和實際彈性之分。而不管是名義彈性或實際彈性，都存在量化水平單一、參數對預測結果影響較大等問題[14-26]。

由圖4 可以看出，相較于彈性系數法，本文提出的大數據預測算法得到的結果普遍與真實值更接近或吻合，即基于動態、靜態分量與3D 卷積的帶寬預測方法具有很好的穩定性及適用性。

4 結語

本文提出的網格化空間帶寬預測方法，以區域控制性規劃為基礎，將預測用地細分為小網格，并依據小網格內部自身數據建立靜態數據集，同時考慮各網格空間距離關系，在搭建動態數據集的前提下，通過3D 卷積的方式捕捉網格動態發展特性，最終將靜態結果與動態結果相結合，可以準確預測帶寬分布情況，得到信息流量密度，為帶寬規劃提供科學的數據支撐。