基于埋地金屬管道雜散電流的腐蝕與防護
封 瓊,張亞萍,汪 洋,于濂清,李 焰
(1. 中國石油大學(華東) 理學院,青島 266580; 2. 中國石油大學(華東) 機電工程學院,青島 266580)
基于埋地金屬管道雜散電流的腐蝕與防護
封 瓊1,張亞萍1,汪 洋1,于濂清1,李 焰2
(1. 中國石油大學(華東) 理學院,青島 266580; 2. 中國石油大學(華東) 機電工程學院,青島 266580)
采用實驗室模擬的方法研究來自直流運輸系統產生的雜散電流對埋地金屬管道腐蝕的影響,并通過強絕緣性能的涂層保護、雜散電流收集網、犧牲陽極保護、排流跨接保護等措施來有效減輕或消除雜散電流對埋地金屬管道的腐蝕。結果表明:采取這幾種防護措施在一定程度上均可以緩解雜散電流帶來的腐蝕問題,其中排流跨接的保護效果最佳。然而在實際施工過程中,單一的防護措施均存在一定的局限性,需要綜合考慮雜散電流的大小以及其他管道的情況,采用靈活有效的防護措施。
雜散電流;埋地管道;涂層;雜散電流收集網;犧牲陽極;排流跨接
在直流牽引供電系統中(如圖1),由于鋼軌對地存在電流泄漏[1]和電位梯度[2],并非全部牽引電流由鋼軌流回牽引變電所,有一部分電流離開了指定導體,在原來不應該有電流的導體中流動。這種沒有按照期望的路徑流動的電流叫做雜散電流,又叫迷走電流[3]。鋼軌中的電流越大,或鋼軌對地的絕緣程度越差,泄漏到地下的雜散電流也就越大。在機車附近,雜散電流從鋼軌流向金屬管道,使金屬管道對地電位較負從而形成陰極區。在變電所附近,雜散電流從金屬管道流回鋼軌和變電所,使金屬管道對地電位較正從而形成陽極區,雜散電流流出管道的地方將發生電解現象,使金屬管道溫度升高而遭受腐蝕[4-5]。本工作從雜散電流腐蝕機理出發,通過對埋地金屬管道采用強絕緣性能的涂層保護、雜散電流收集網、犧牲陽極保護、排流跨接保護等措施來有效減輕或消除雜散電流腐蝕,為雜散電流腐蝕的研究提供試驗依據。
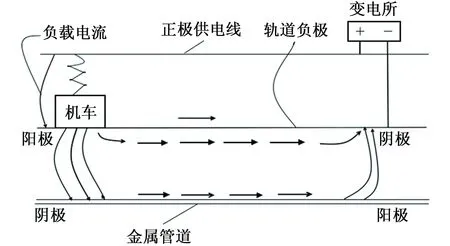
圖1 直流運輸系統雜散電流示意圖Fig. 1 Schematic diagram of stray current from DC transportation system
1 試驗
最能直接反映出埋地金屬管道雜散電流干擾腐蝕程度的是雜散電流的大小,但由于受到實際條件限制,電氣化鐵路雜散電流無法直接測出,而管道受干擾腐蝕程度的主要判別依據為管地電位和土壤電位梯度(該方法稱為電氣判別法)。其中管地電位是最重要的參數,它既可以反映管道的腐蝕特性,又可以反映雜散電流的干擾特性。因此可以把管地電位作為雜散電流腐蝕效果評估的重要指標之一。
圖2為雜散電流測定原理圖。在一個絕緣性能良好的長方體塑料箱內充滿土壤,塑料箱的尺寸為80 cm×60 cm×70 cm。金屬管道采用直徑4.0 mm,長40.0 cm的電阻絲(按1∶100縮小)。牽引變電所外加電壓為7.5 V。
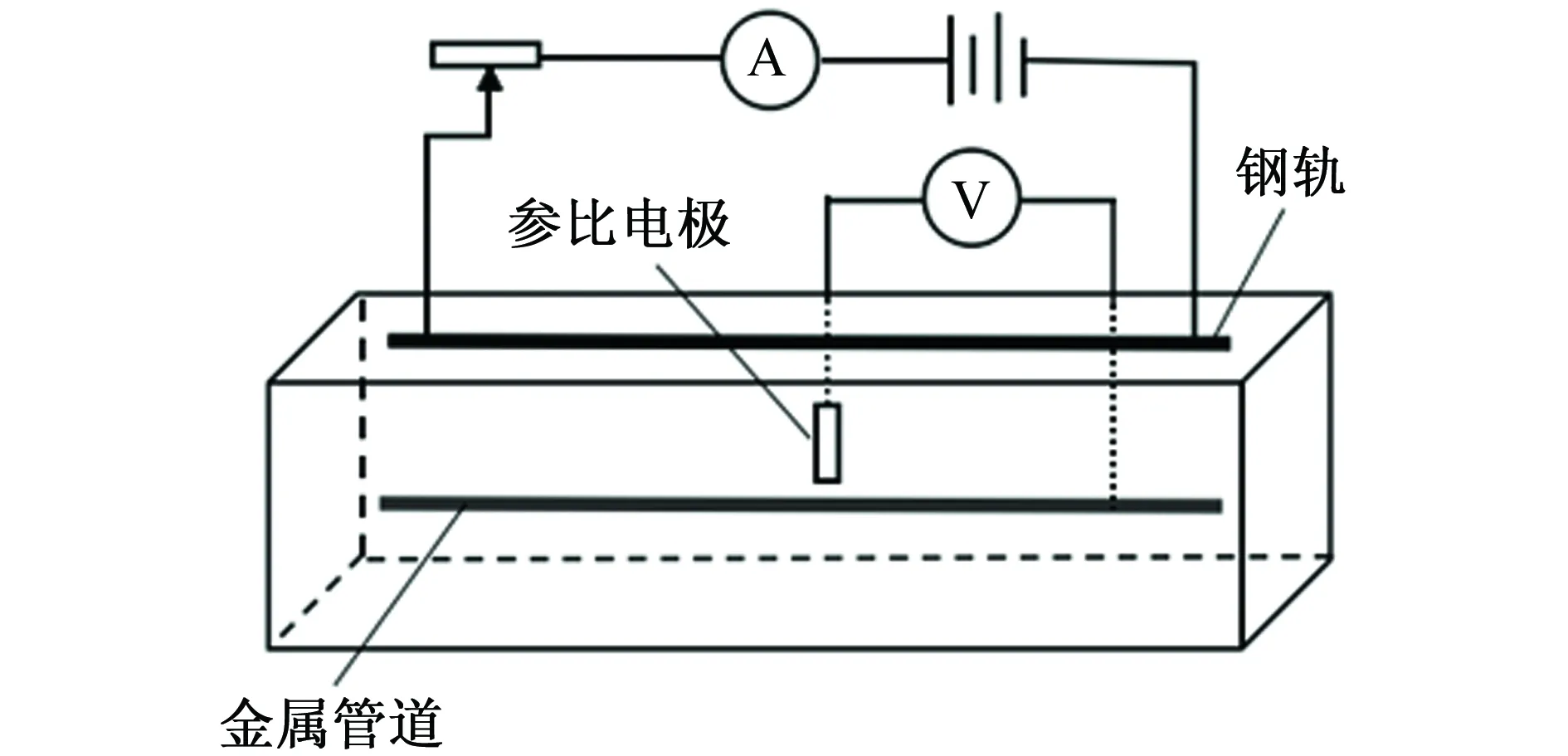
圖2 雜散電流測定原理圖Fig. 2 Principle diagram of stray current measurement
將一根電阻絲埋于土壤中一定深度,模擬埋地金屬管道。另一根電阻絲放置于土壤表面,用來模擬鋼軌,外接直流電源。在埋地金屬管道上選擇五個測試點,用導線將每個測試點連接到土壤表面。將數字萬用表一端連接在與測試點相連的導線處,另一端連接銅/硫酸銅參比電極。數字萬用表測得的電壓即為管地電位。
2 結果與討論
2.1 涂層對管地電位的影響
圖3給出了測量深度為4.0 cm,無任何保護措施和外加涂層保護下埋地金屬管道不同測試點的管地電位。其中測量深度為鋼軌與埋地金屬管道的垂直距離。
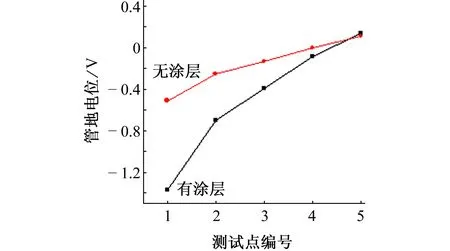
圖3 測試點的管地電位Fig. 3 Pipe-to-soil potentials of test points
由圖3可見,無論是有涂層還是無涂層,遠離牽引變電所測試點1的管地電位較負,而最靠近牽引變電所的測試點5的管地電位較正,該處的金屬管道由于雜散電流的流出而作為原電池的陽極,因而發生電解作用使得管道遭受較嚴重的腐蝕。對比有、無涂層條件下的管地電位可知,外加涂層并不能較好地達到減輕金屬管道腐蝕的效果。這可能是由于泄漏到地下的雜散電流過大,或者涂層質量不佳,存在較小面積的破損使得雜散電流流入從而加重腐蝕程度。
由此可見,使用強絕緣性能的涂層保護雖然有利于減少流入管道的雜散電流總量,但是一旦涂層出現破損現象,就會使得流入金屬管道的雜散電流更集中,雜散電流腐蝕的危險性有增無減。
2.2 埋地深度對管地電位的影響
由圖4可見,隨著埋地深度的增加,金屬管道(有涂層)的管地電位呈現降低趨勢,雜散電流腐蝕程度逐漸減輕。這主要是由于雜散電流腐蝕的本質是電化學腐蝕的電解過程,隨著埋地深度的增加,土壤對離子遷移的阻力也會相應增大,因此到達金屬管道的離子數目會有一定的減少,陽極電解效應將會減弱。此外,當管道埋地深度增加時,氧的傳輸過程也會受到一定程度的抑制。腐蝕過程中,溶解氧不斷地在金屬表面還原,大氣中的氧就不斷地溶入土壤并向金屬表面輸送。氧輸送過程如圖5所示,氧以對流或擴散的方式通過土壤,隨著埋地深度的增加,氧傳輸過程受到的擴散阻力也會隨之增大,陰極極化反應會受到一定程度的阻礙,因此陽極溶解反應速率變慢,雜散電流腐蝕程度得以減輕。

圖4 不同埋地深度下測試點的管地電位Fig. 4 Pipe-to-soil potentials of test points at different buried depths

圖5 氧的傳輸過程示意圖Fig. 5 Diagram of oxygen transmission process
在一定深度范圍內,隨著管道埋地深度的增加,雜散電流腐蝕程度會相應地減弱。因此,在實際施工時,可通過合理設計埋地管道的深度來緩解雜散電流帶來的腐蝕問題。
2.3 鋪設雜散電流收集網對管地電位的影響
在鋼軌與金屬管道(有涂層)之間鋪設雜散電流收集網,其示意圖如圖6所示。雜散電流收集網由上、下兩排縱向鋼筋組成,每排有五根φ12.0 mm鋼筋,每隔10.0 cm用一根φ25.0 mm的橫向鋼筋將五根縱向鋼筋焊接成一整體,同時用兩根φ20.0 mm鋼筋把上、下二層橫向連接鋼筋焊成一體。鋪設的雜散電流收集網的縱向電阻要小于埋地金屬管道的縱向電阻,以達到收集雜散電流使之通過收集網回到牽引變電所負極的目的。
圖7為在使用涂層保護的基礎上,鋼軌與金屬管道之間鋪設雜散電流收集網前后各測試點埋地金屬管道的管地電位。由圖7可見,鋪設雜散電流收集網后,金屬管道的管地電位降低,表明管道在雜散電流收集網作用下得到了較好的保護。但是使用收集網后最靠近牽引變電所的測試點5的管地電位只降到了-0.073 V,可見試驗中鋪設的雜散電流收集網裝置對雜散電流的收集效果并不是特別理想,有待于進一步改進。
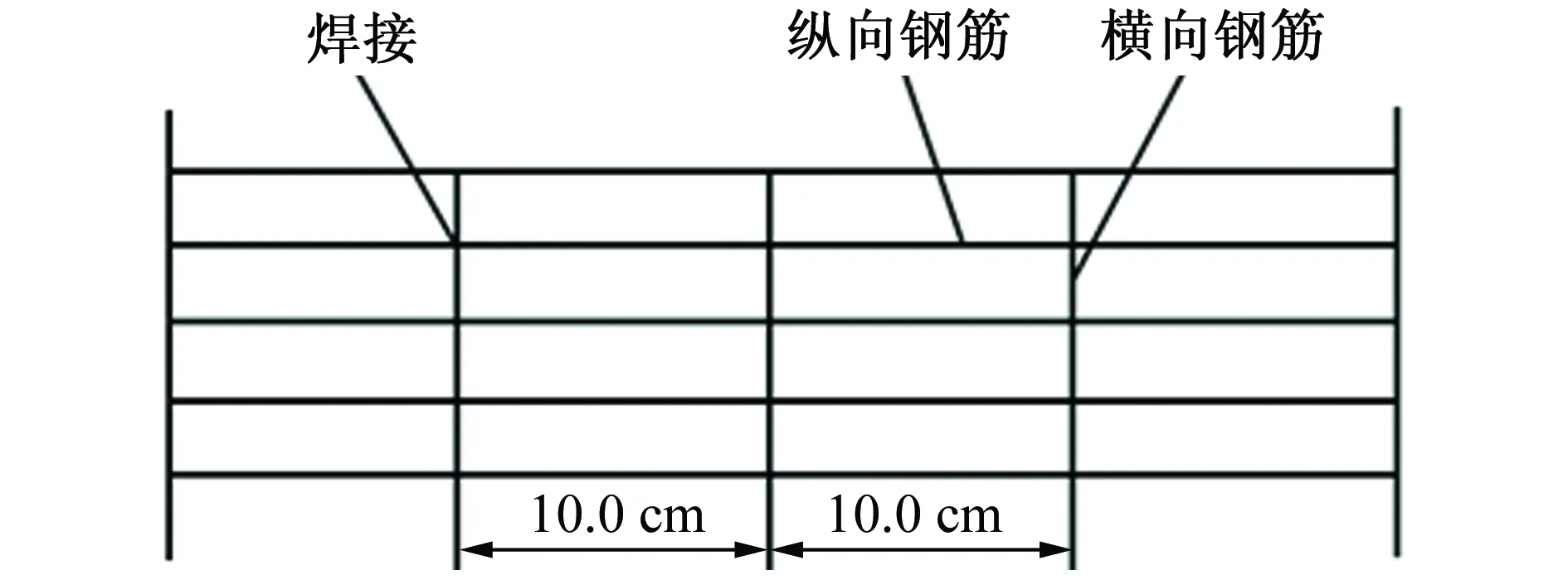
圖6 雜散電流收集網示意圖Fig. 6 Diagram of stray current collection network

圖7 鋪設雜散電流收集網前后各測試點的管地電位Fig. 7 Pipe-to-soil potentials of test points before and after laying stray current collection network
圖8為雜散電流收集網的等效電路圖。圖8中:r為牽引網阻抗;R為鋼軌阻抗;Rg為鋼軌對地電阻;Rt為埋地金屬管道等效電阻;RI為雜散電流收集網等效電阻;I為牽引電流;Ig為雜散電流。
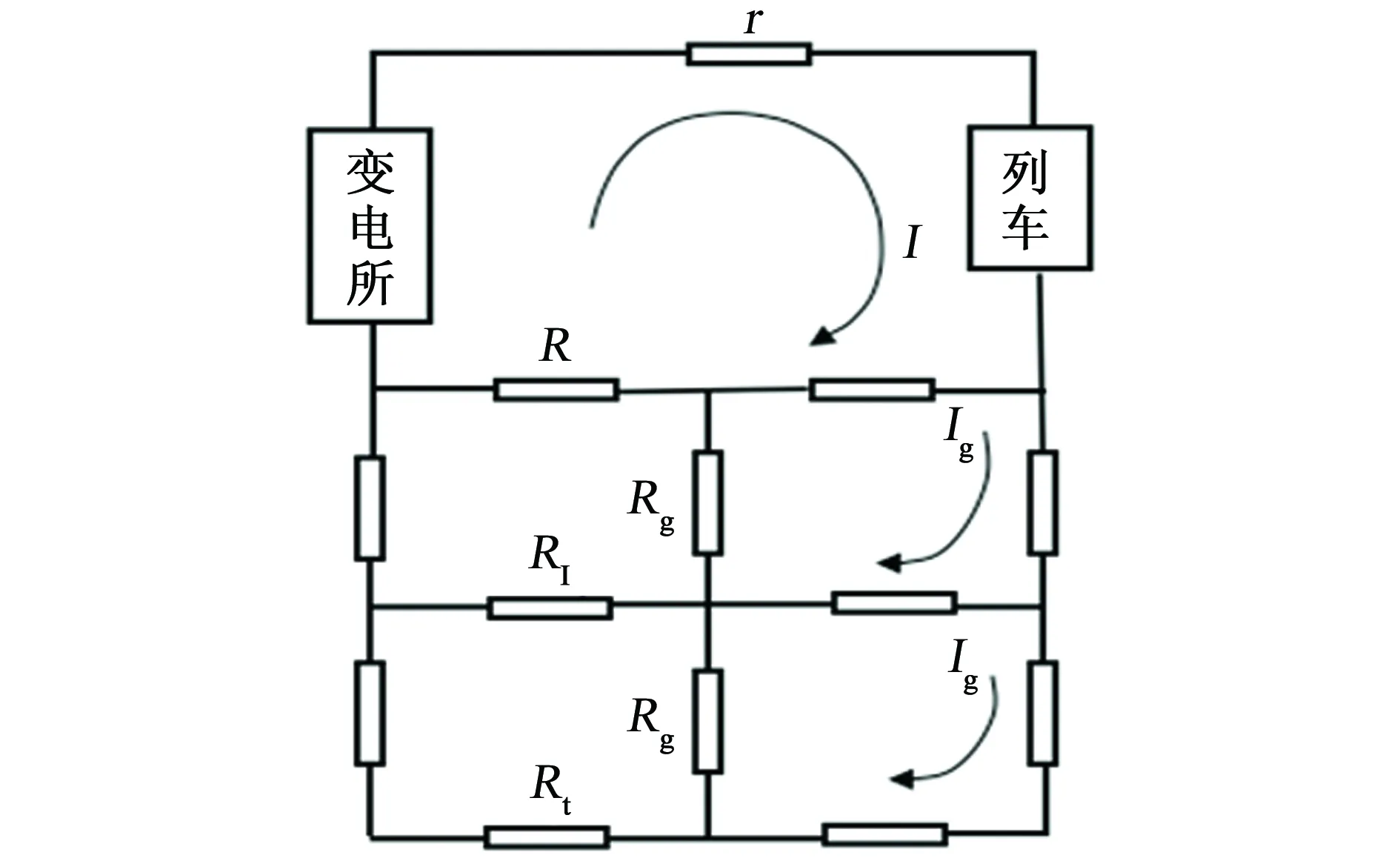
圖8 雜散電流收集網等效電路圖Fig. 8 Equivalent circuit diagram of stray current collection network
由圖8可以看出,鋪設雜散電流收集網相當于給雜散電流增加了一條分流支路,且要求雜散電流收集網的縱向電阻比埋地金屬管道的縱向電阻小,因此通過雜散電流收集網的雜散電流會多一些,這樣就達到了收集雜散電流的效果,埋地管道得到一定程度的保護。
鋪設雜散電流收集網為雜散電流提供了返回牽引變電所的低電阻通路,以限制雜散電流繼續向系統以外泄漏,減少雜散電流對金屬管道及金屬構件的腐蝕。使用雜散電流收集網對減輕雜散電流腐蝕產生了較好的效果,可以作為地鐵設計、施工及運營中雜散電流防護的參考。但是要實現理想的收集效果,需要對收集網的設計與布置提出更高的要求。
2.4 犧牲陽極保護對管地電位的影響
犧牲陽極的陰極保護法是一種電化學保護技術,由金屬的化學特性可知,腐蝕原電池的陰極不發生腐蝕,只有陽極才發生腐蝕。犧牲陽極保護法的原理是將被保護的金屬管道與活性陽極相連。一般所選的陽極金屬要有足夠負的穩定電位,且陽極極化小,溶解均勻。鎂陽極具有電位負,可獲得較大的驅動電壓,極化率低,單位質量發生電量大等特點,盡管電流效率低,但仍是犧牲陽極的理想材料[6-7]。圖9為犧牲陽極保護裝置示意圖。
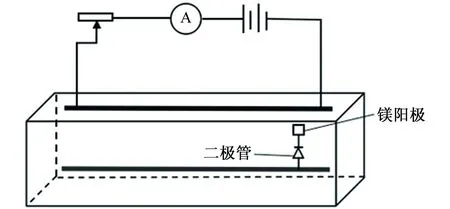
圖9 犧牲陽極保護裝置圖Fig. 9 Set-up diagram of sacrificial anode protection
圖10為使用鎂犧牲陽極保護前后金屬管道(有涂層)管地電位的變化規律。由圖10可見,使用犧牲陽極保護措施后各測試點的管地電位降低幅度均比較大,雜散電流腐蝕得到較大程度的減輕。這主要是由于被保護管道金屬與犧牲陽極構成宏觀的腐蝕電池,電位較正的金屬成為宏觀腐蝕電池的陰極,電位較負的金屬成為陽極[8]。陽極在電解質中優先產生電子,為被保護金屬提供陰極保護電流,并不斷溶解持續對陰極進行陰極極化[9],從而使金屬腐蝕發生的電子遷移得到抑制,避免或減弱腐蝕的發生。
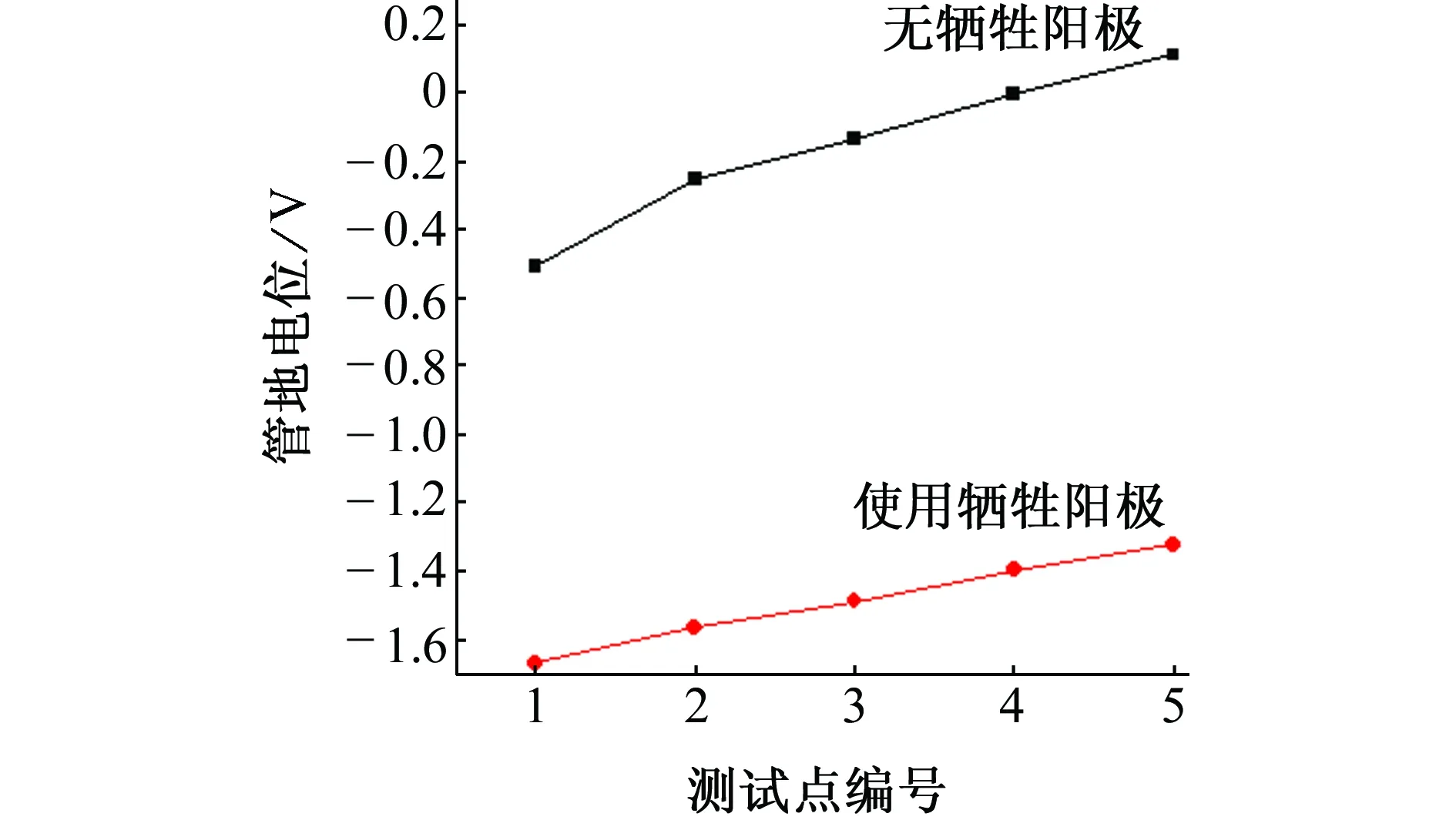
圖10 犧牲陽極保護前后各測試點的管地電位Fig. 10 Pipe-to-soil potentials of test points before and after sacrificial anode protection
當施加陰極保護電流使陰極發生極化時,系統總電位向負方向移動,腐蝕電流減小,腐蝕速率降低。當電位移動到陽極的初始極化電位時,系統的腐蝕電流降為零,腐蝕停止,陰極得到徹底的保護。因此使用金屬鎂作為犧牲陽極能有效地使腐蝕系統的電位負移從而降低腐蝕速率。但是,當陰極保護電位過負時將發生析氫反應,產生的氫原子滲入金屬將導致氫脆破壞,應予以避免。由于金屬鎂的電位較負,從而失去電子成為陽極而遭受腐蝕;而大量的O2和OH-向鐵附近移動,發生陰極反應從而對金屬管道起到一定的保護作用。
犧牲陽極保護法是以電位足夠負的金屬作為陽極,通以直流電流進行陰極極化,使被保護金屬處于陰極狀態從而達到阻止金屬腐蝕的一種方法。電位較負的金屬失去電子被氧化而受到腐蝕,電位較正的金屬作為陰極得到電子而被保護。犧牲陽極金屬和被保護金屬之間的電位差是腐蝕過程的推動力,電位差越大,表明犧牲陽極金屬能提供更多的保護電流。由測試結果可知,犧牲陽極與涂層保護的配合使用,在埋地金屬結構的防腐施工工藝中應用前景可觀,經濟效益明顯,應予以大力推廣。
2.5 排流跨接保護對管地電位的影響
排流跨接法就是將埋地結構物與地鐵鋼軌連接起來,使進入結構物的泄漏電流返回鋼軌的方法。排流法有直接排流跨接法、極性排流跨接法和強制排流跨接法三種[10]。為了防止電流的反向流動,試驗中采用如圖11所示的極性排流跨接保護將埋地金屬管道與地鐵鋼軌連接起來,以達到阻斷逆流的目的。
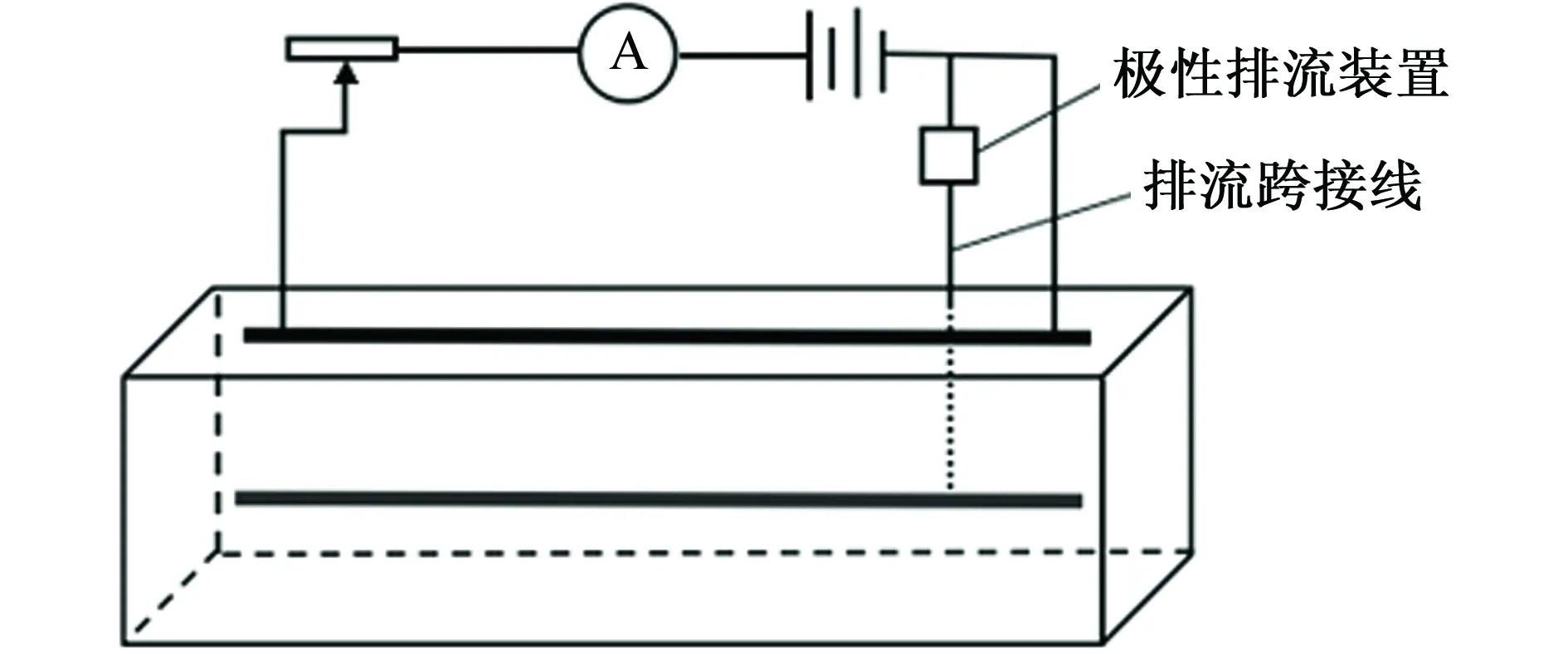
圖11 排流跨接保護原理圖Fig. 11 Principle diagram of current drainage and bridging protection
由圖12可以看出,四種措施對埋地金屬管道(有涂層)均起到一定的保護作用,其中使用極性排流跨接保護對減輕埋地金屬管道雜散電流腐蝕的效果最為明顯。極性排流裝置的核心器件是硅二極管,主要起正向導通、反向截止的極性排流作用。當埋地金屬管道相對走行鋼軌電位差為正值時,二極管正向導通使雜散電流通過,管道上的雜散電流經由排流裝置流回電源負極,使整個管道變為陰極性,從而避免雜散電流直接從管道流入土壤造成電化學腐蝕,防止了陽極溶解過程[11]。
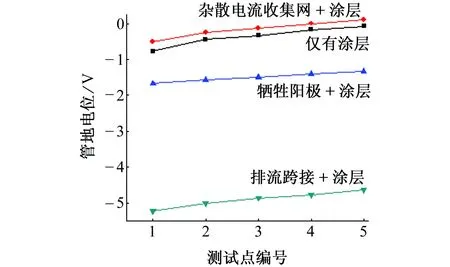
圖12 幾種保護措施下各測試點的管地電位Fig. 12 Pipe-to-soil potentials of test points under different measures of protection
但是排流跨接保護會導致運輸系統總的負極回路接地電阻降低,使得運輸系統的總雜散電流量增加,同時加劇在跨接前遭受雜散電流干擾較小的管道的腐蝕。由圖13可見,使用排流跨接后加大了其他未受保護管道的雜散電流干擾。這種干擾產生的原因在于:排流量過大時,會增大雜散電流量及軌地電位差。

圖13 排流跨接對未保護管道影響Fig. 13 Effects of current drainage and bridging protection on unprotected pipeline
使用極性排流跨接保護可以在一定程度上減小直流雜散電流干擾,但同樣會使總的雜散電流增大而加劇腐蝕。如果干擾源停運,就會使保護體得不到保護。當排流量過大時,對其他鄰近未受保護管道的干擾腐蝕也會加大。同時,使用極性排流跨接保護容易造成電位過負的現象。當直流雜散電流干擾嚴重時,使用極性排流裝置并不能完全消除直流雜散電流。因此有必要開發新型的智能排流設施,避免目前直流雜散電流排流設施“排正不排負”的弊端。
3 結論與建議
3.1 結論
(1) 當雜散電流通過直流牽引運輸系統時,在埋地金屬管道靠近變電所的區域容易發生放電現象,導致該部位的金屬與周圍電解質成為陽極,發生電解反應,從而產生雜散電流腐蝕。
(2) 對埋地金屬管道使用高絕緣性能的涂層保護可以在埋地深度較大時保護管道,使其免受雜散電流腐蝕,但是管道與鋼軌靠得太近時,由于雜散電流太大以及無法保證實際施工時的涂層是完好的,該方法的保護效果不佳。
(3) 在使用涂層保護的基礎上使用雜散電流收集網或者犧牲陽極的陰極保護法可以在一定程度上緩解雜散電流帶來的腐蝕問題,但是這兩種措施對于降低靠近變電所附近區域管道的管地電位效果都不太明顯。使用排流跨接保護可以在較大程度上減輕雜散電流腐蝕,但是這種方法會加大其他未受保護管道的雜散電流腐蝕影響。
上述幾種保護措施,都存在一定的局限性,因此在直流牽引運輸系統周圍鋪設金屬管道時,要綜合考慮雜散電流的大小以及其他管道的情況,靈活采用有效的保護措施。
3.2 建議
(1) 基于以上防護措施各自的優缺點,建議對上述措施進行聯合使用來彌補彼此的不足,如雜散電流收集網與排流裝置聯合使用[12],犧牲陽極與排流裝置聯合使用[13]等,這些措施已在試驗研究中得以驗證,但并未大量應用到實際施工中去,主要是因為其具體硬件配置與設計還不完全清晰,有待于進一步開發完善。
(2) 鑒于雜散電流存在環境的特殊性與復雜性,對埋地管道雜散電流的監測與防護存在較大的障礙,因此實現雜散電流數字化監控將成為雜散電流研究發展的必然趨勢,是今后治理雜散電流腐蝕問題的關鍵。
[1] 趙紅梅. 雜散電流腐蝕防護技術基礎研究[D]. 大連:大連理工大學,2007.
[2] JONES D A. Effect of alternating current on corrosion of lowalloy and carbon steels[J]. Corrosion,2013,34(12):428-433.
[3] 曹阿林. 埋地金屬管線的雜散電流腐蝕與防護研究[D]. 重慶:重慶大學,2010.
[4] 封瓊,張亞萍,余豪,等. 土壤電阻率對埋地管道雜散電流腐蝕影響的研究進展[J]. 應用物理,2015,5(9):1-7.
[5] 趙宇輝. 地鐵雜散電流腐蝕及其對隧道結構可靠度和耐久性的影響[D]. 成都:西南交通大學,2006.
[6] 汪洋,張亞萍,韓雪,等. 減小來自陰極保護裝置雜散電流干擾的實驗研究[J]. 現代物理,2015,5(3):65-71.
[7] 胡士信. 陰極保護工程手冊[M]. 北京:化學工業出版社,1991:60-64.
[8] 張寶宏,叢文博,楊萍. 金屬電化學腐蝕與防護[M]. 北京:化學工業出版社,2005:155-157.
[9] 文九巴,馬景靈,賀俊光. 防腐用鋁基陽極材料[M]. 北京:化學工業出版社,2012:47-51.
[10] 朱孝信. 地鐵的雜散電流腐蝕與防護[J]. 材料開發與應用,1997,12(5):43-44.
[11] 許瑞,王建華,周毅. 基于電氣化鐵路雜散電流的埋地輸油管道腐蝕及防護探討[J]. 中國儲運雜志,2011:102-104.
[12] 牛安心. 地鐵雜散電流腐蝕防護研究[D]. 成都:西南交通大學,2011.
[13] 騰延平,張永盛,王禹欽,等. 雜散電流排流設施有效性評價研究[J]. 管道技術與設備,2012(4):40-54.
Corrosion and Protection of Buried Metal Pipelines Based on Stray Current
FENG Qiong1, ZHANG Ya-ping1, WANG Yang1, YU Lian-qing1, LI Yan2
(1. College of Science, China University of Petroleum (East China), Qingdao 266580, China;2. College of Mechanical and Electrical Engineering, China University of Petroleum (East China), Qingdao 266580, China)
Simulation test in laboratory was carried out to study the impact of stray current produced by DC transportation system on buried metal pipelines. The measures such as coating protection, stray current collection network, sacrificial anode protection, current drainage and bridging protection were taken to mitigate or eliminate stray current corrosion of buried metal pipelines effectively. The results show that using these protective measures can bring certain remission to corrosion problems caused by stray current, among which drainage and bridging protection had the best effect. However, in practical construction process, single measure has certain limitation, so it is necessary to comprehensively consider the intensity of stray current and the situations of other pipelines, and take protective measures flexibly and effectively.
stray current; buried pipeline; coating; stray current collection network; sacrificial anode; current drainage and bridging
10.11973/fsyfh-201702002
2015-10-08
國家自然科學基金面上項目(21476262); 青島市科技成果轉化引導項目(14-2-4-108-jch); 大學生創新計劃項目
張亞萍(1967-),副教授,碩士,從事納米材料的合成、制備及其性能研究,材料腐蝕與檢測等相關工作,0532-86983418,zhangyp@upc.edu.cn
TG174
A
1005-748X(2017)02-0091-05

