希沃白板助力菱形教學

李明　張新全

【摘要】《教育信息化2.0行動計劃》指出要積極推進“互聯網+教育”發展，堅持信息技術和課堂教學深度融合.希沃白板作為信息化教學而設計的互動教學平臺，能夠完美的將兩者結合.本文以一節示范課“菱形”為例，呈現出希沃白板在幾何教學中的優越性.

【關鍵詞】希沃白板;菱形;數學課堂教學

本教學案例來自一位優秀教師的部級優課.上課內容為滬科版數學八年級下冊《矩形菱形正方形》第二課時，教師將希沃白板技術融入到數學課堂中去，讓學生清晰地觀察到菱形的幾何特征，有利于學生的學習，是一節精彩生動的數學課.本文將對此案例進行展示和分析，由此說明希沃白板融入到幾何教學中的優勢.

1教學目標的確定

菱形作為矩形后的第二種特殊的平行四邊形，它既具有平行四邊形所有的特征，又具有后面將要學習的正方形的部分特征，是一個非常重要的平面幾何圖形，對研究信息技術與數學課堂教學的融合，具有典型性.

（1）理解并掌握菱形的定義、性質和面積公式.

（2）類比矩形的研究思路，經歷探索菱形性質的過程，體會研究幾何的一般思路，進一步提高學生的邏輯推理能力.

（3）在操作活動和觀察、分析過程中發展學生主動探究的習慣，體會數學圖形的美妙.

2教學重難點的確定

重點菱形的定義、性質，利用菱形的性質解決相關幾何問題.

難點菱形性質的探索及其應用.

3教學流程的確定

（1）復習舊知，引入新知

師：同學們，前面我們學習了平行四邊形的定義、性質以及判定，然后將平行四邊形從角的角度特殊化，特殊在什么地方，大家回顧一下.（教師操作希沃白板，如圖1—3.）

生：有一個角為直角.

師：此時這個圖形就變成了矩形，那么平行四邊形還能從哪些角度將它特殊化呢？

生：邊.

師：邊可以怎么特殊呢？大家看一看.（教師操作希沃白板，如圖4—6.）

師：在這中間有沒有什么特殊的狀態？

生：有一組鄰邊相等.

師：這樣的圖形叫做菱形，這也是我們今天要學習的主要內容即菱形.（教師板書課題）

設計意圖教師利用希沃白板展示了一個一般性的平行四邊形，通過在白板上操作，使其中一角特殊化為直角，學生很直觀地看到了從平行四邊形變化到矩形的過程，以此引導學生進行了前面內容的的復習，這里設計巧妙的是，教師提問學生除了從角特殊化，還能從哪方面特殊化，以此問題為基礎，再次利用希沃白板的特性，移動平行四邊形一邊，將平行四邊形變為一組鄰邊相等的平行四邊形即菱形，引出新課題，整個過程只通過了一個平行四邊形的變化，簡潔而又直觀！

（2）師生合作，探索新知

師：那么什么叫菱形呢？大家關注一下這個變化的過程，哪位同學能不能用一句話總結一下，給菱形下一個定義.

生：有一組鄰邊相等的平行四邊形叫做菱形.（學生觀察圖7—8獲取菱形特征）

師：菱形要滿足兩個條件：有一組鄰邊相等;平行四邊形.

師：本節課，我們重點研究它的性質，那么應該從哪些角度研究它的性質呢？

生：邊、角、對角線.

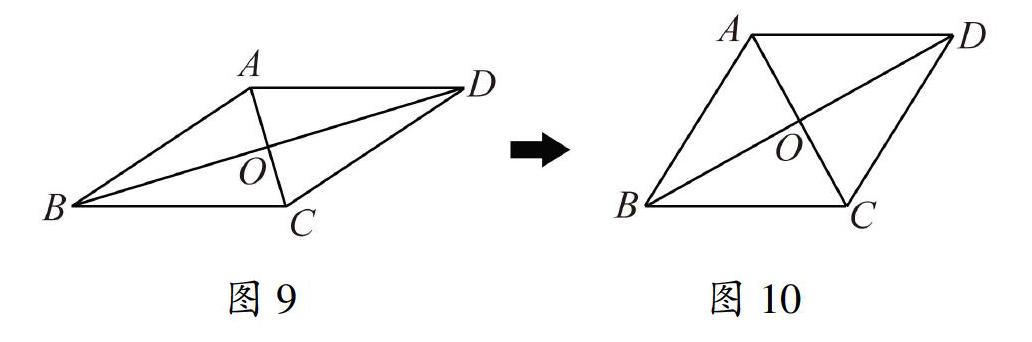
教師展示一個動態的菱形ABCD，連接對角線，假設交點為O，如圖9—10所示.

師：思考一下，在變化的過程中，它的邊有哪些固定的關系，角有哪些固定的關系，對角線呢？大家可以先獨立思考一下，和同桌交流一下.

生：我覺得四條邊都相等.（AB=BC=CD=DA）

師：還有嗎？

生：AD∥CB，AB∥DC.

師：角，你們看到了哪些東西？

生：我認為∠ABC=∠ADC，∠BAD=∠BCD.

師：那么對角線呢？

生：AC⊥BD，BO=DO，AO=CO.

師：剛剛大家從邊、角、對角線角度發現了這么多關系，前提是這個圖形是菱形，那么我們能不能證明這些關系成立？

生：由于菱形是平行四邊形，所以有AD∥CB，AB∥DC的結論，對于證明AB=BC=CD=DA，因為菱形兩組對邊分別相等，并且一組鄰邊相等，所以菱形的四邊都是相等的.

師：我們知道AD∥CB，AB∥DC是平行四邊形已有的性質，而AB=BC=CD=DA不是平行四邊形已有的性質，故AB=BC=CD=DA是菱形第一個獨特的性質.

教師板書性質1：菱形的四條邊都相等.

師：對于角之間的關系需不需要過多的討論呀？

生：不需要，平行四邊形的對角就相等，菱形是特殊的平行四邊形，所以∠ABC=∠ADC，∠BAD=∠BCD肯定成立.

師：那么對角線呢，BO=DO，AO=CO這層關系需不需要過多的說明呀？

生：不需要.

師：為什么呢？

生：平行四邊形的性質，對角線相互平分.

師：那么為什么AC⊥BD，請一位同學說明一下.

生：首先，據性質1，我們知道菱形的四條邊相等，所以AB=AD，說明△ABD是一個等腰三角形，又因為BO=DO，所以AO是平分BD的，根據等腰三角形的“三線合一”，所以AC⊥BD.

師：他主要用到的是什么知識？

生：三線合一.

師：很好，通過大家的上述證明，我們發現AC⊥BD，我們把它作為菱形的性質2.

教師板書菱形的性質2：菱形的對角線互相垂直.

師：正因為這些獨特的結論，使得菱形具有很美妙的圖形特征.我們可以看到AC垂直平分BD，BD垂直平分AC.我們知道垂直平分線就會容易想到什么特殊的圖形特征？

生：軸對稱

師：它有哪幾條對稱軸？

生：AC或BD所在的直線.

教師板書：菱形是軸對稱圖形，它的兩條對角線所在的直線都是它的對稱軸.

設計意圖這個新知探索過程從最初的猜想到證明再到最后的歸納.特別是在學生自己觀察時，傳統教學中，學生很難通過一個固定的菱形找出菱形所具有的性質，一個大小固定的菱形也很難讓學生信服四邊都相等和對角線互相垂直，而通過希沃白板上動態的圖形演示，學生可以容易猜想出菱形所特有的這些特征.

（3）講練結合，鞏固新知

問題1已知菱形ABCD的邊長為13cm，對角線AC長為10cm.

（1）菱形ABCD的周長為cm;

（2）另一邊對角線BD的長為cm;

問題2現有一張菱形紙片，請通過適當裁剪，重新拼成一個矩形，有哪些不同的拼法？

在問題2中，師生借助希沃白板給出了2種裁剪方式，如圖11—14和圖15—18所示.

設計意圖問題1主要是鞏固菱形的兩個主要性質;問題2教師利用了希沃白板的特性，課前已經將菱形切分好，只需請同學上臺移動菱形的部分使之組成一個矩形，同時通過了第二種裁剪后，由學生通過觀察圖形易證明出菱形的面積公式S=12ab（a，b為菱形的兩條對角線長）.

（4）課堂小結，學習展望

師生共同回顧本節課所學，并重點強調了菱形的定義、性質、對稱軸和菱形的面積公式，比如菱形具有平行四邊形沒有的性質：四邊相等和對角線相互垂直.并帶領學生展望了后面學習的內容，比如菱形的判定方法和更加特殊的平行四邊形即正方形.4教學啟示

在這節數學課堂中，教師借助希沃白板能夠讓學生更加直觀地觀察到菱形在變化的過程中，邊、角、線各自之間的數量和位置關系，充分地展現了希沃白板與數學課堂教學融合的優勢.結合本節課教學內容，我們認為希沃白板的教學啟示主要體現在以下幾個方面.4.1拉近師生距離，提高教學效率

希沃白板作為數學課堂教學中的輔助工具，成為了教師和學生之間溝通的媒介之一，師生都可以參與到希沃白板的操作中來，拉近了師生距離.在備課時，教師可以將自己提前做好的PPT課件直接插入到希沃白板里;在課上，教師可以通過手機版希沃白板操作課件同步顯示在電腦屏幕上，不受空間限制.教師也能在課堂上隨手拍下學生的典型錯題上傳到電腦屏幕上，供教師教學所用;在課后，教師也能利用白板上保存的板書進行教學反思并修改，以便下次更好地教學.總之，在課前、課中和課后都能極大地提高教師的教學效率.4.2建立校園庫，實現資源共享

在希沃白板上，教師能夠保存自己制作的課件，上傳至云端，課件內容不容易丟失，自己能不斷地積累資源，形成自己的課件資源庫，下次上課時，自己在資源庫里創作的課件也能隨時使用.同時，數學教師可以在學校建立一個校園資源庫，將自己制作的課件上傳庫里，實現校內資源共享，我們甚至可以去網絡資源庫游覽全國各地教師制作的優質課件.

4.3玩轉圖形，提升直觀想象

課堂中借助希沃白板技術，使得學生能夠對于復雜的數學內容有著清晰的認識.以這節課為例，教師先展示一個靜態的平行四邊形，再讓圖形動起來，能很輕易地將一般性的平行四邊形通過角的特殊化變為矩形，也能通過邊的特殊化變為一個菱形.在探究菱形的性質過程中，學生也能夠透過一個動態的菱形變化過程，自己猜想出邊、角、對角線各自的位置和數量關系.后面教師借助希沃白板讓學生上臺動手操作，進行菱形的裁剪，直觀地展現了菱形通過裁剪拼成矩形的過程.這種強大的操作性在其他的幾何圖形中也是適用的，例如我們可以利用希沃白板去探究三角形的內角和定理，向學生直觀演示三角形通過裁剪拼成一個平角，有助于提升學生的直觀想象能力.4.4服從教學設計，達到預期目標

希沃白板上的內容并不是教師隨意設計的，每一步的設置都是有它的道理，而如何設置希沃白板里的內容，離不開課前的教學準備.我們知道教材的編寫要依據課程標準，所以教材是符合課程標準要求的，數學教師通過對教材深入分析，編寫教學設計，這里的教學設計和教材是保持一致的.至此，在傳統數學教學中課前準備就已基本完成了，而在信息化教學里，希沃白板里的課件內容則要依據教學設計設置，其內容要服從于教學設計，不能夠脫離于這個系統之外[1].那么這樣的希沃白板內容可以說是比較接近課程標準的要求，才能真正地改善教學過程，實現教學預期目標.

參考文獻

[1]劉衛平.技能·應用·反思——交互式電子白板應用的教學思考[J].中國信息技術教育，2009（15）：5-7.