均質(zhì)細(xì)桿在純滾動圓環(huán)內(nèi)的運動

王樹平

（河北建筑工程學(xué)院數(shù)理系，河北 張家口 075000）

文獻(xiàn)［1-2］分析了質(zhì)點在可自由移動的圓弧形凹槽上的運動，文獻(xiàn)［3］對在光滑水平面上可自由移動的圓弧形凹槽內(nèi)作純滾動的圓柱體的運動進(jìn)行了分析.以上文獻(xiàn)中的兩個運動物體所組成的系統(tǒng)都是動量守恒的保守系統(tǒng).本文將對在粗糙水平面上可純滾動的圓環(huán)內(nèi)的均質(zhì)細(xì)桿的運動進(jìn)行分析，導(dǎo)出了細(xì)桿的質(zhì)心在慣性參考系中的運動軌跡方程和系統(tǒng)的運動微分方程；求出了圓環(huán)內(nèi)的細(xì)桿微振動的周期，在此基礎(chǔ)上，分別得到了細(xì)桿在靜止的圓環(huán)內(nèi)以及細(xì)桿在可自由移動的圓環(huán)內(nèi)微振動的周期，質(zhì)點在可作純滾動的圓環(huán)內(nèi)以及質(zhì)點在靜止不動圓環(huán)內(nèi)微振動的周期.

如圖1所示，在足夠粗糙的水平面上置一質(zhì)量為m1，徑為R的均質(zhì)圓環(huán)，而在圓環(huán)內(nèi)有一質(zhì)量為m2，長度為l（l＜2R）的均質(zhì)細(xì)桿，初始時刻，二者中心連線OC與豎直方向夾角為θ0，均質(zhì)細(xì)桿由靜止開始相對圓環(huán)滑動（桿與環(huán)之間無摩擦力），由于細(xì)桿的運動，圓環(huán)由靜止開始相對于地面作純滾動.

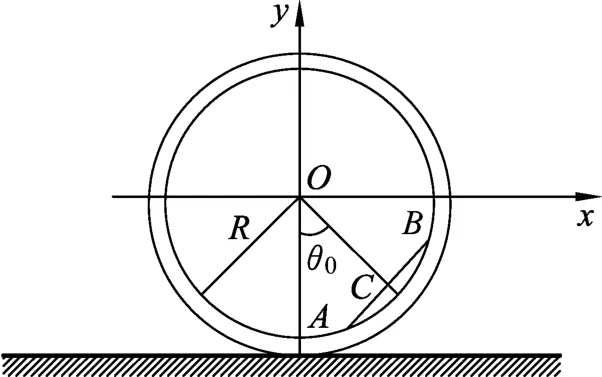
圖1 初始時刻的細(xì)桿和圓環(huán)

為了討論方便，首先建立坐標(biāo)系，如圖1和圖2所示.以初始時刻圓環(huán)的中心為坐標(biāo)原點O，Ox軸水平向右，Oy軸豎直向上，建立靜止的慣性參照坐標(biāo)系Oxy；然后，以任意時刻圓環(huán)的中心為坐標(biāo)原點O，Ox軸水平向右，Oy軸豎直向上，建立平動坐標(biāo)系Oxy.對本系統(tǒng)而言，有兩個自由度，選O點的水平坐標(biāo)x及OC連線與豎直向下的方向的夾角θ為廣義坐標(biāo).

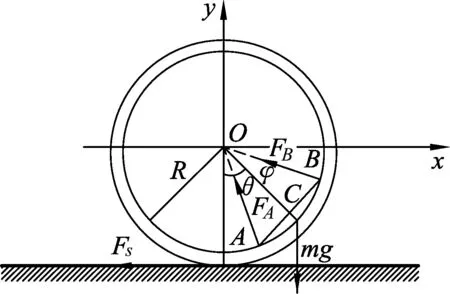
圖2 細(xì)桿的受力分析

1 均質(zhì)細(xì)桿的質(zhì)心運動軌跡

對圓環(huán)和均質(zhì)細(xì)桿的運動分析如下.圓環(huán)作平面運動，質(zhì)心O的速度為，轉(zhuǎn)動的角速度為，角加速度為；均質(zhì)細(xì)桿也作平面運動，它的質(zhì)心C作復(fù)合運動，牽連運動為隨同基點O的平動，牽連速度為，相對運動為繞基點O點的圓周運動，相對速度vr=.絕對速度的平方為

2 系統(tǒng)的運動微分方程的建立

3 細(xì)桿在圓環(huán)內(nèi)微振動的周期

4 討論

4.1 細(xì)桿在靜止的圓環(huán)內(nèi)微振動的周期

眾所周知，當(dāng)m1?m2，即圓環(huán)質(zhì)量遠(yuǎn)遠(yuǎn)大于細(xì)桿的質(zhì)量，這時，圓環(huán)可看作靜止不動，于是由式（26）得到桿在靜止的圓環(huán)內(nèi)微振動的周期為

4.2 細(xì)桿在位于光滑水平面上的圓環(huán)內(nèi)做微振動的周期

其他已知條件不變，當(dāng)圓環(huán)放在光滑水平面上時，其不受水平面的摩擦力作用，也就是沒有使圓環(huán)由靜止轉(zhuǎn)動起來的力矩，于是伴隨著細(xì)桿在環(huán)內(nèi)的運動，圓環(huán)只能在水平面上純滑動，這時，用與上述相同的思路和方法容易得到，細(xì)桿在位于光滑水平面上的圓環(huán)內(nèi)微振動的周期為

4.3 質(zhì)點在可作純滾動的圓環(huán)內(nèi)微振動的周期

當(dāng)R?l時，即圓環(huán)半徑遠(yuǎn)遠(yuǎn)大于細(xì)桿的長度時，這時細(xì)桿可看成質(zhì)點，于是由式（26）得到一個質(zhì)點在可作純滾動的圓環(huán)內(nèi)微振動的周期為

4.4 質(zhì)點在靜止不動圓環(huán)內(nèi)微振動的周期

當(dāng)m1?m2并且R?l，由式（26）得到一個質(zhì)點在靜止不動圓環(huán)內(nèi)微振動的周期為

這是我們熟知的結(jié)論.