拓展模型遷移 培養(yǎng)數(shù)學(xué)應(yīng)用能力
——以一道典型力學(xué)題的拓展教學(xué)分析

楊 勇

（貴州省安順市關(guān)嶺民族高級(jí)中學(xué)，貴州 安順 561300）

對(duì)物理問(wèn)題的探究與拓展，有助于促進(jìn)知識(shí)的建構(gòu)、知識(shí)的遷移應(yīng)用、著力于面向解決實(shí)際問(wèn)題的思維層次性發(fā)展，通過(guò)對(duì)物理問(wèn)題的探討與分析，對(duì)問(wèn)題的拓展與遷移，對(duì)學(xué)生的學(xué)科素養(yǎng)的提升和創(chuàng)新思維能力的培養(yǎng)具有重要作用.同時(shí)物理解題的拓展與分析，促進(jìn)學(xué)生創(chuàng)新思維能力的提升，優(yōu)化學(xué)生創(chuàng)新思維，把核心素養(yǎng)教學(xué)目標(biāo)落到實(shí)處.

1 例題呈現(xiàn)

如圖1所示，一盛水容器繞豎直中心軸線勻速轉(zhuǎn)動(dòng)，試證明容器轉(zhuǎn)動(dòng)時(shí)，容器中的水面為一拋物面.

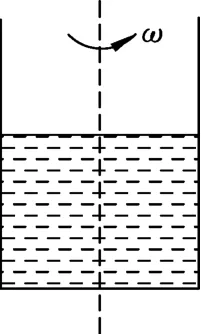
圖1

2 典例問(wèn)題教學(xué)分析

2.1 液體內(nèi)部某點(diǎn)的受力分析

當(dāng)容器以一定的角速度轉(zhuǎn)動(dòng)時(shí)，容器邊沿的水會(huì)沿著邊沿上升，中間部分水會(huì)往下凹.如圖2所示，在液面的最低點(diǎn)建立如圖所示的直角坐標(biāo)系，在坐標(biāo)原點(diǎn)沿著x軸方向的一段橫截面積為ΔS，長(zhǎng)度為x的水平液柱，假設(shè)水的密度為ρ，大氣壓強(qiáng)為p0，由于該液柱隨著容器一起做勻速圓周運(yùn)動(dòng)，液柱左側(cè)受到的壓力為F1=p0ΔS，液柱右側(cè)的壓強(qiáng)p=p0+ρgy，所以右側(cè)受到的壓力為F2=（p0+ρgy）ΔS，則液柱隨著容器做勻速圓周運(yùn)動(dòng)的向心力有左右兩側(cè)的壓力差來(lái)提供可得F向=F2-F1.因此向心力F向=ρgyΔS.

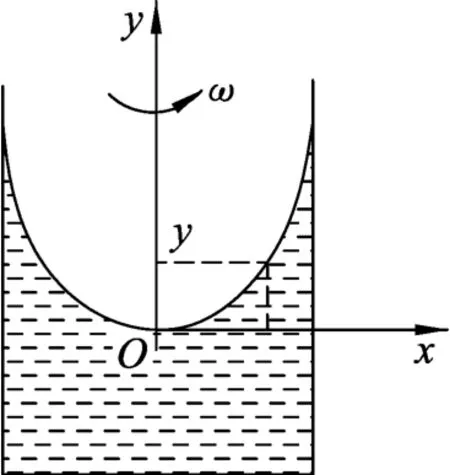
圖2

這是一條拋物線方程.由于在液面上所有的點(diǎn)都滿足上式的方程，所以液面的曲線為一條拋物線，同理由這些線構(gòu)成的面自然也是拋物面，因此容器轉(zhuǎn)動(dòng)時(shí)隨容器一起轉(zhuǎn)動(dòng)的液體的表面為一拋物面.

2.2 液面上某點(diǎn)的受力分析

在液體表面取一質(zhì)量很小的質(zhì)點(diǎn)m，對(duì)該質(zhì)點(diǎn)的受力分析如圖3所示.該質(zhì)點(diǎn)做勻速圓周運(yùn)動(dòng)的向心力由支持力與重力的合力提供，設(shè)支持力的作用線與y軸的夾角為θ，則受力F向=mg tanθ.該質(zhì)點(diǎn)的橫坐標(biāo)為x，則

圖3

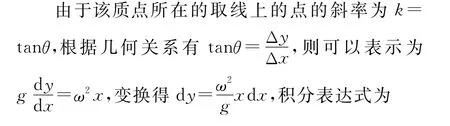
由于曲面上所有點(diǎn)的受力都有相同的特點(diǎn)，因此都滿足上式的函數(shù)方程，由于上式是拋物線方程，則液面形成的即為拋物面.

2.3 引入非慣性系，對(duì)液面上任意質(zhì)點(diǎn)靜止的條件

如圖4所示，選擇隨水一起轉(zhuǎn)動(dòng)的的容器為參考系，水相對(duì)于容器靜止，引入慣性力f慣=mω2x，引入慣性力后液體表面所選的質(zhì)點(diǎn)的受力平衡可知，

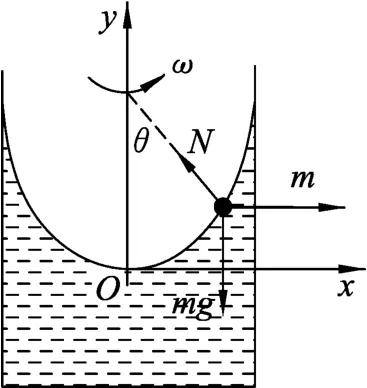
圖4

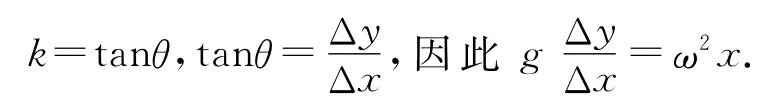
可得液體隨容器轉(zhuǎn)動(dòng)時(shí)形成的液面為一拋物面.

以上從3個(gè)角度對(duì)容器中液體隨容器轉(zhuǎn)動(dòng)時(shí)得到的曲面為一個(gè)拋物面，由于在某恒定的角速度轉(zhuǎn)動(dòng)時(shí)，液體的運(yùn)動(dòng)性質(zhì)為同軸轉(zhuǎn)動(dòng)，角速度相等，應(yīng)用角速度相等及液體受力特點(diǎn)結(jié)合圓周運(yùn)動(dòng)的性質(zhì)，從受力角度、向心力來(lái)源、建立坐標(biāo)等物理與數(shù)學(xué)的結(jié)合分析和證明液面為一拋物面.從不同角度對(duì)學(xué)生思維的激發(fā)和能力素養(yǎng)的培養(yǎng)，激發(fā)學(xué)生對(duì)問(wèn)題的思考.

2.4 不同角速度下的曲面形狀

3 拓展探究教學(xué)分析

3.1 繩子約束下的圓周運(yùn)動(dòng)對(duì)比與分析

如圖5所示，用一根細(xì)繩長(zhǎng)為l一端系一個(gè)小球，另一端固定，給小球不同的初速度，使小球在水平面內(nèi)做角速度不同的圓周運(yùn)動(dòng).根據(jù)圓周運(yùn)動(dòng)的特點(diǎn)有

圖5

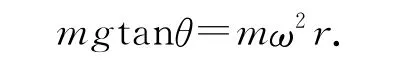
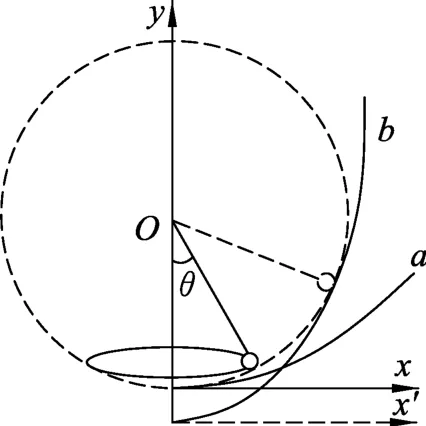
圖6

3.2 錐面約束下的圓周運(yùn)動(dòng)對(duì)比與分析

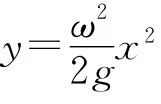
圖7

3.3 桿約束下的圓周運(yùn)動(dòng)對(duì)比與分析

如圖8所示，質(zhì)量為m小圓環(huán)穿在光滑的桿上，小環(huán)能以相同的角速度ω在任意地方隨桿做勻速圓周運(yùn)動(dòng)，結(jié)合所學(xué)的知識(shí)分析桿的形狀.

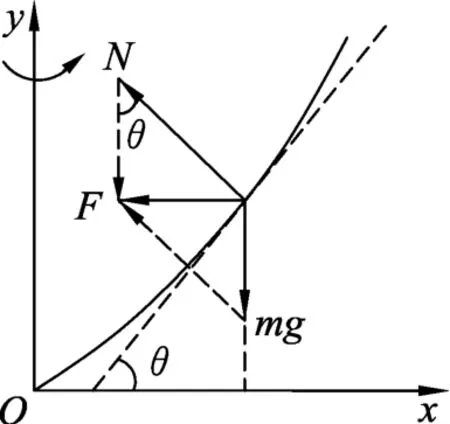
圖8

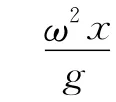
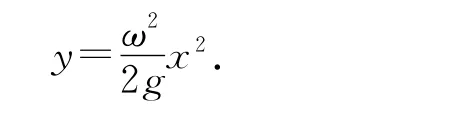
因此光滑桿約束與光滑面約束具有相同的特點(diǎn)，要讓物體能以大小相等的角速度在任意位置做勻速圓周運(yùn)動(dòng)滿足的條件必須是一個(gè)拋物形狀的桿或者是一個(gè)拋物面，才能具有這樣的特點(diǎn).同理，可以發(fā)現(xiàn)為什么在光滑的錐面上小球做圓周運(yùn)動(dòng)的角速度不相等，如果能通過(guò)這樣的一個(gè)拋物面的規(guī)律應(yīng)用于相應(yīng)具有一定約束錐擺的圓周運(yùn)動(dòng)中，可以使解決問(wèn)題到達(dá)事半功倍.

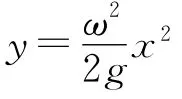
3 總結(jié)

對(duì)于以上的分析，從一到同軸轉(zhuǎn)動(dòng)問(wèn)題的解法的分析，找到處理問(wèn)題的方法，通過(guò)典例分析，聯(lián)系常見的繩子約束、錐面約束、桿約束條件下的圓周運(yùn)動(dòng)的特點(diǎn)，找到具有相等的角速度的圓周錐擺運(yùn)動(dòng)滿足一個(gè)拋物面的特點(diǎn)，從而培養(yǎng)學(xué)生分析問(wèn)題，應(yīng)用數(shù)學(xué)知識(shí)解決問(wèn)題，應(yīng)用知識(shí)遷移的學(xué)科素養(yǎng).這樣的拓展與分析在教學(xué)中能讓學(xué)生的形成良好的思考習(xí)慣，創(chuàng)新思維能得到提升，同時(shí)，通過(guò)問(wèn)題與知識(shí)遷移、模型對(duì)比等形式的教學(xué)分析和討論，讓學(xué)生主動(dòng)獲取知識(shí)，發(fā)展探究的能力，在解決探究問(wèn)題的過(guò)程中加深對(duì)原有知識(shí)的認(rèn)知結(jié)構(gòu)，形成物理知識(shí)體系，克服思維單一、方法傳統(tǒng)的保守習(xí)慣的弊端.讓學(xué)生在探究過(guò)程中找到成就感，體驗(yàn)獲得知識(shí)的喜悅，形成合作交流的團(tuán)體，增強(qiáng)學(xué)生的集體意識(shí)，樹立正確的學(xué)習(xí)觀念，通過(guò)探究學(xué)習(xí)的過(guò)程體驗(yàn)，培養(yǎng)學(xué)生的創(chuàng)新思維，真正落實(shí)物理學(xué)科核心素養(yǎng)的教學(xué)目標(biāo).