人工杉木林林分空間結構參數分析及相關性研究

賴敏華, 賴日文, *, 胡仁杰, 葉偉

人工杉木林林分空間結構參數分析及相關性研究

賴敏華1, 賴日文1, *, 胡仁杰1, 葉偉2

1. 福建農林大學林學院, 福州 350002 2. 福建省林業勘察設計院, 福州 350001

基于南平松溪林場九個人工杉木林標準地的實測數據, 對人工杉木林林分空間結構參數進行了評價和相關性分析, 為制定杉木林和其他純林林分空間結構優化和調整措施奠定基礎。采用=4確定林木的空間結構單元, 用大小比數、角尺度和競爭指數等3個林分空間結構參數分析杉木林的林分空間結構特征。結果表明, 9個標準地的杉木林大小比數都接近中庸狀態, 林木個體差異不大, 林木分化不嚴重; 角尺度處于均勻和隨機分布狀態之間, 與水平分布理想模式存在一定差距; 競爭指數較為穩定, 沒有因為年齡的不同而出現大幅度的變動。大小比數和競爭指數間為中度相關, 大小比數和角尺度, 以及角尺度和競爭指數間幾乎不相關。研究結果有助于杉木人工林的可持續經營。

杉木; 大小比數; 角尺度; 競爭指數; 相關性

0 前言

培育生態系統健康, 生態功能豐富并且穩定的森林是現代森林經營管理的主要目標, 這個目標能否實現在很大程度上取決于林分是否具有合理的空間結構[1]。林分空間結構在森林經營管理過程中是最有可能進行調控的因子[2], 對其進行分析并優化是培育可持續經營森林至關重要的途徑。惠剛盈指出, 林分空間結構能夠反映林分內不同物種之間的空間分布關系, 并且描述林分中與林木分布位置有關的空間信息[3]。對林分空間結構特征的掌握, 有助于對其進行優化和調整, 對于模擬森林結構未來的發展趨勢, 保持和維護森林生態系統的多種功能, 以及指導植被的恢復和重建都具有重要意義[4]。

目前, 大家對于林分空間結構的研究主要集中在四個方面:一是通過分析林分空間結構, 對其進行優化調整, 之后評價調整效果, 為林分空間結構的改善提供指導。張今朝[5]等對陳大國有林場的生態公益林進行林分空間結構的研究, 擬定合理的擇伐措施, 預測的調整效果顯示林分結構得到良好改善; 王智勇[6]等利用威布爾分布函數(weibull)和角尺度、混交度、大小比3個林分空間結構參數對落葉松天然次生林的水平結構及空間結構進行綜合分析。二是依托可視化技術與森林經營技術, 對各項森林經營活動進行模擬研究。董靈波[7]等以帽兒山樟子松人工林為研究對象, 以可視化模擬為手段, 建立森林經營的可視化模型, 為森林經營管理者提供一個全新的決策平臺。三是聚焦于林分空間結構參數的N元分布。張崗崗[8]等以甘肅小隴山銳齒櫟天然混交林為例, 借助結構參數 N 元分布全面、系統地揭示林分結構特征, 探索了其結構信息的高效可視化表達; 四是對各個空間結構參數進行多目標規劃。曹小玉[9]等在分析杉木生態公益林林分空間結構的基礎上提出評價指標, 并將其劃分為 5 個評價等級, 較客觀地反映了杉木生態公益林的林分空間結構。但其提出的空間結構評價指數是以各個空間結構參數對理想空間結構的貢獻相同為前提的, 有的學者對此存在異議, 認為林分空間結構參數(Stand spatial structure parameters)[10]之間具有一定的相關性, 應該弄清它們之間的相互作用機制, 從而為確定各林分空間結構參數的權重提供依據。此外, 研究參數之間的相關性, 也能在林分空間結構的實際調查、優化調整過程中提供指導。本文在分析大小比數(Neighborhood comparison)[11]、角尺度(Uniform angle index)[12]、競爭指數(Tree competition indexes)[13]這三個空間結構參數的基礎上, 采用SPSS對這三個參數之間的相關性進行了分析研究, 揭示其中的關系, 為森林經營管理措施提供可參考的科學依據。

1 材料與方法

1.1 研究區概況

松溪國有林場位于福建省南平市松溪縣, 地處118°42'00″—118°44'35″, 27°13'00″—27°32'16″。屬于亞熱帶季風氣候, 夏季高溫多雨, 冬季溫和少雨, 四個季節有明顯變化, 夏季時間長, 冬季時間短, 春早秋遲。年平均溫度為18.5 ℃, 年平均太陽福射量為4088 MJ·m-2, 年平均降雨量為1679 mm。屬于福建與浙江交界的仙霞嶺南伸支脈, 地勢由北向南傾斜, 松溪貫穿全境。海拔為200—600 m, 坡度在20°—40°之間。地勢沒有較大起伏, 屬于低山丘陵區域。山脊走向由西北延伸至東南。土類以紅壤為主, 黃紅壤兼而有之。水分、養分沿著山坡向下移動, 導致山坡上部的土壤脊薄且肥力低下。中下部的土壤大多是黃紅壤, 具有較大的土層厚度, 為中壤或輕壤質地, 土壤肥力高。松溪縣地帶性植被為常綠闊葉林帶。然而, 由于頻繁的人為經營管理活動, 當地的植被已經被破壞, 大多數地方是常綠針葉林。主要喬木樹種有馬尾松 ()、杉木 ()、木荷 ()、青剛櫟 ()、酸棗 ()等。

1.2 研究方法

1.2.1 標準地調查

在松溪國有林場新鋪工區的人工杉木林中設置9塊標準地, 使用羅盤儀測角, 用皮尺量20.00 m的距離, 從而使標準地大小為20.00 m×20.00 m, 并在標準地四角埋設固定標樁。為綜合考慮各齡級的林木不同生長情況及林分空間結構特征, 在幼齡林、中齡林、近成熟林中各設置了3塊標準地, 依次順序編號。標準地內海拔200—250 m, 位于南坡的下坡位, 土壤類型為紅壤。對標準地中所有胸徑大于5 cm的杉木進行每木檢尺, 獲取胸徑以及樹高等數據, 并掛牌編號, 記錄枯立樹及死樹等。使用Postex林地定位儀定位每株林木的相對位置, 并用GPS測量每個標準地東北角、西北角、西南角、東南角和中心點的坐標, 從而轉換每株林木的相對位置坐標到整個定位系統內, 確定每株林木的具體地理位置。

1.2.2 空間結構單元的確定

空間競爭單元為林木中任意一株中心木和與它距離最近的株鄰近木所構成的空間結構關系, 本文基于=4來表達, 從而對人工杉木林空間結構的特征進行分析。邊界木處于標準地邊緣, 可能會受到相鄰區域的影響, 并且它的鄰近木可能處于標準地的外部, 以此邊界木為中心木所建立的空間結構單元是不準確的, 會對空間結構分析的結果產生一定的影響, 為此必須對標準地進行邊緣矯正[14]。本文采用的是距離緩沖區法, 即在標準地四周設置帶狀緩沖區, 寬度為2 m, 該寬度可以充分消除邊界效應的影響, 并充分利用標準地內的調查數據。

1.2.3 空間結構分析參數的選取

目前, 國內外的許多學者在定義和計算林分空間結構指數時主要考慮3個方面, 即樹種之間的隔離度、林木競爭以及林木空間分布格局。樹種隔離度(Isolation of trees)[15]通常用混交度(Mingling degree)[16]來表示, 在傳統混交度的基礎上發展了多樣性混交度、基于Voronoi圖計算的混交度指標等。林木競爭(Trees competition)[17]的概念在100多年前就被提出, 發展至今日, 已有各種不同的衡量方法, 主要分為與距離有關和與距離無關的競爭指數兩大類。惠剛盈等提出的大小比數能夠用于描述單株林木的生長優勢, 被很多學者成功用于林分空間結構的分析中。毛沂新等采用胸徑作為大小比數的度量變量, 計算出大小比數并應用于遼東山區原始闊葉紅松林主要樹種空間結構的分析[18]。在林木空間分布格局方面, 角尺度由于不需要測距并且可以用于表示單株林分或整個林分的分布而被廣泛使用。以上幾個空間結構參數在國內外被廣泛用于分析林分空間結構、恢復重建林分以及動態模擬的研究中[19-20]。由于本文研究的是人工杉木純林, 因此不需對混交度進行研究。在調查中使用Postex林地定位儀對每株林木進行了精確的相對定位, 因而使用與距離有關的Hegyi競爭指數來更加準確描述林木間的競爭關系, 與大小比數和角尺度進行聯合分析, 探討三者是否具有關聯性。

(1)大小比數

大小比數(U)是指胸徑、樹高或者冠幅大于中心木的鄰近木的株數占所有鄰近木株數的比例, 能夠反映樹種之間的大小分化的程度, 本研究中采用胸徑的大小來對其進行衡量, 其公式為[8]:

式中: 當中心木大于鄰近木時,K=0;否則,K=1。

(2)角尺度

角尺度(W)用于描述圍繞中心木的4株鄰近木分布位置的均勻性, 并且可用于分析樹木的空間分布格局。任意2株鄰近木有兩個夾角, 將小角設置為, 將標準角a視為鄰近木均勻分布時的夾角(a=72°)[21]。W則被定義為小于標準角a的角個數在所考察的4個夾角中的所占比例, 其公式為:

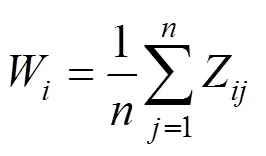
式中: 當中心木與第株鄰近木的夾角大于標準角a時,Z為0, 否則為1;為鄰近木株數。

(3)競爭指數

競爭指數反映林木個體所承受的競爭壓力, 林分生長造成的營養和生活空間的缺乏不可避免地引起林木種內和種間的激烈競爭, 從而導致林窗產生、林木死亡等, 由此引起林分空間結構的變化。因此, 在林分空間結構分析因子的選取中, 競爭指數是一個關鍵因子。盡管與距離無關的林木競爭指數在實際調查研究中較容易獲得, 但由于沒有諸如林木具體分布位置之類的空間信息, 因此應用范圍不是很廣。而與距離有關的競爭指數雖然較難獲得, 但因為考慮了林木的空間信息, 計算結果較為可靠, 因此被廣泛使用。

在以往的眾多競爭指數模型中, Hegyi 提出的距離預測模型已經得到了較多認可和廣泛使用[22]。因此, 本文采用Hegyi競爭指數來表示林木競爭強度, 其計算公式為:

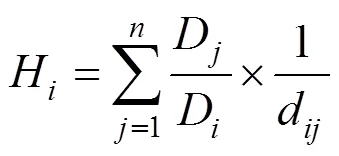
式中:D為中心木的胸徑,D為鄰近木的胸徑,d為中心木與鄰近木之間的距離。

1.3 空間結構參數相關性研究

空間結構參數之間存在相互作用機制, 參數之間具有一定的相關性。因此本文首先利用SPSS軟件對大小比數、角尺度和競爭指數進行了正態性檢驗, 得到它們的sig(顯著性)分別為0.090, 0.160, 和0.102, 均大于0.05, 服從正態分布, 可以進行Pearson相關性分析。而后對各個標準地的空間結構參數進行雙變量Pearson相關性分析, 分析大小比數、角尺度和競爭指數之間是否具有相關性, 比較三個標準地之間的相關性數據, 以驗證結果是否具有準確性。<0.05時表示相關顯著, 即可以明顯的觀察到兩變量的相關, 兩個變量的相關有統計學意義。

2 結果與分析

2.1 人工杉木林林木分布圖

在Winklemass軟件中, 導入每株林木的精確坐標以及胸徑, 使林木呈現在圖上(如圖1)。每個圓點代表一株林木, 圓點大小反映林木胸徑大小。為進行邊緣矯正, 設置2 m寬的緩沖區, 處于緩沖區外的林木視為邊界木, 不以中心木對其進行計算, 僅作為中心木的鄰近木存在, 而將所有位于緩沖區內的林木視為中心木。由于是人工林, 林木整體分布比較均勻, 不存在局部稀疏或密集的現象。此次調查的9個標準地所處的林分經營類型均為集約杉木中徑材, 所以造林密度比較大, 在166—216株每畝之間。

2.2 人工杉木林林分空間結構分析

由表1可知, 杉木幼齡林、中齡林和近成熟林的平均大小比數分別為0.4959, 0.4951和0.4957, 都接近中庸狀態, 說明杉木的胸徑差異不明顯, 大多數林木都處于中等生長狀態, 只有少數的林木占優勢或處于被壓迫狀態, 林木分化不嚴重。平均角尺度分別為0.4822, 0.4582和0.4784, 是均勻分布和隨機分布的中間狀態, 距離隨機分布的理想狀態差距較小。標準地內的杉木林全部為人工林, 林木分布比較規律, 經過林木個體競爭和人工更新后, 一些林木的分布表現出隨機分布的趨勢。平均競爭指數分別為4.5389, 4.5674和4.5136, 在各個年齡都相對穩定, 沒有因為年齡的不同而出現大幅度的變動。

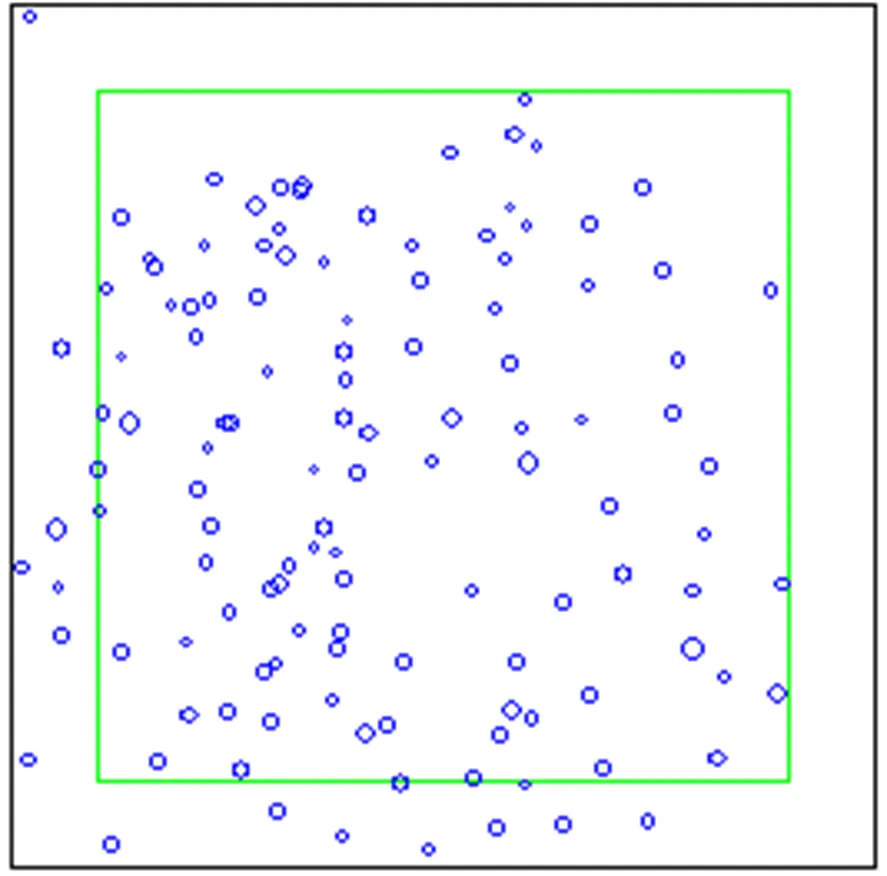
圖1 林木分布

Figure 1 Tree distribution

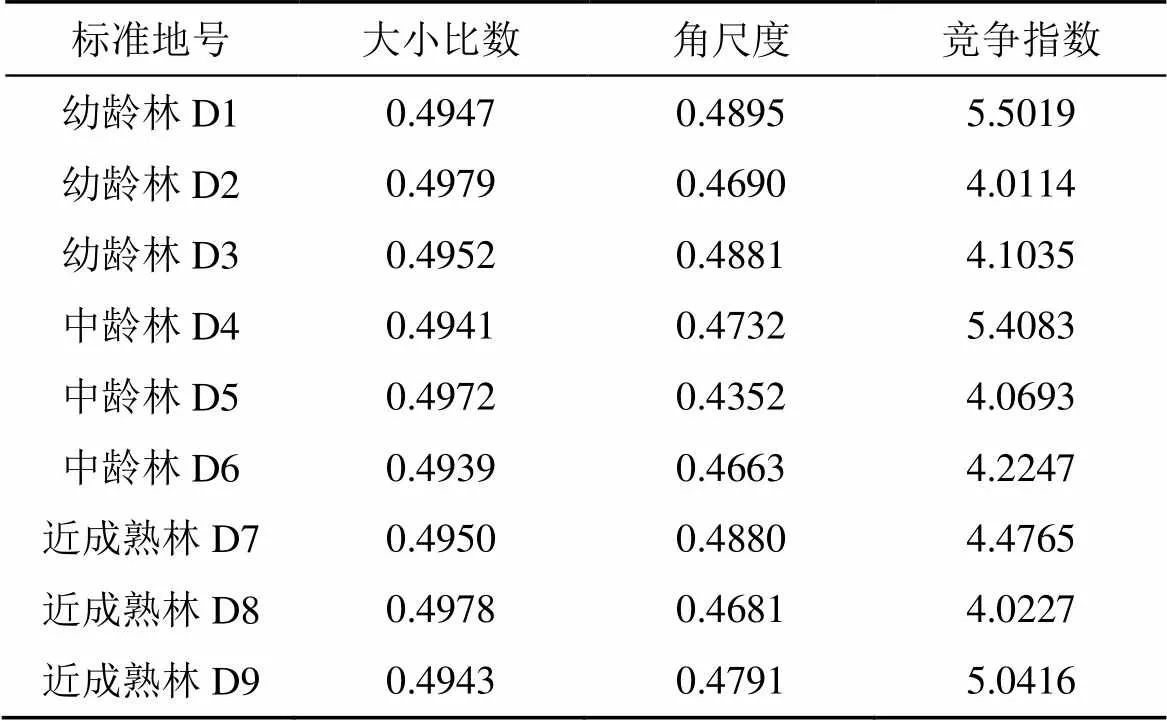
表1 各標準地空間結構參數值

2.3 杉木林林分空間結構參數相關性

由表2可知, 九個標準地中大小比數和角尺度的之間值均大于0.05, 不具有相關性, 沒有統計學意義。角尺度和競爭指數之間的值也均大于0.05, 沒有相關性。這可能是由于人工杉木林在栽種時期分布地較為均勻, 角尺度不會隨著年齡的增長發生太大變化, 處在比較穩定的狀態。而隨著年齡的增長, 林木個體會因為環境、個體差異等因素而產生不同的生長速度, 從而導致大小比數和競爭指數不斷發生變化。因而角尺度與大小比數、競爭指數不具有相關性。

不同與此, 在九個標準地中, 大小比數和競爭指數之間的值均小于等于0.001, 存在相關性。標準地D1、D3、D5、D6、D8的值分別為0.384、0.321、0.391、0.367、0.358, 均接近0.4。而標準地D2、D4、D7、D9的值分別為0.457、0.405、0.413、0.432, 均超過0.4, 說明大小比數和競爭指數之間呈中等相關的關系。這是因為大小比數和競爭指數在計算過程都使用胸徑作為度量指標之一, 所以盡管競爭指數還考慮了單株林木之間的距離, 二者也會在一定程度上具有關聯性。

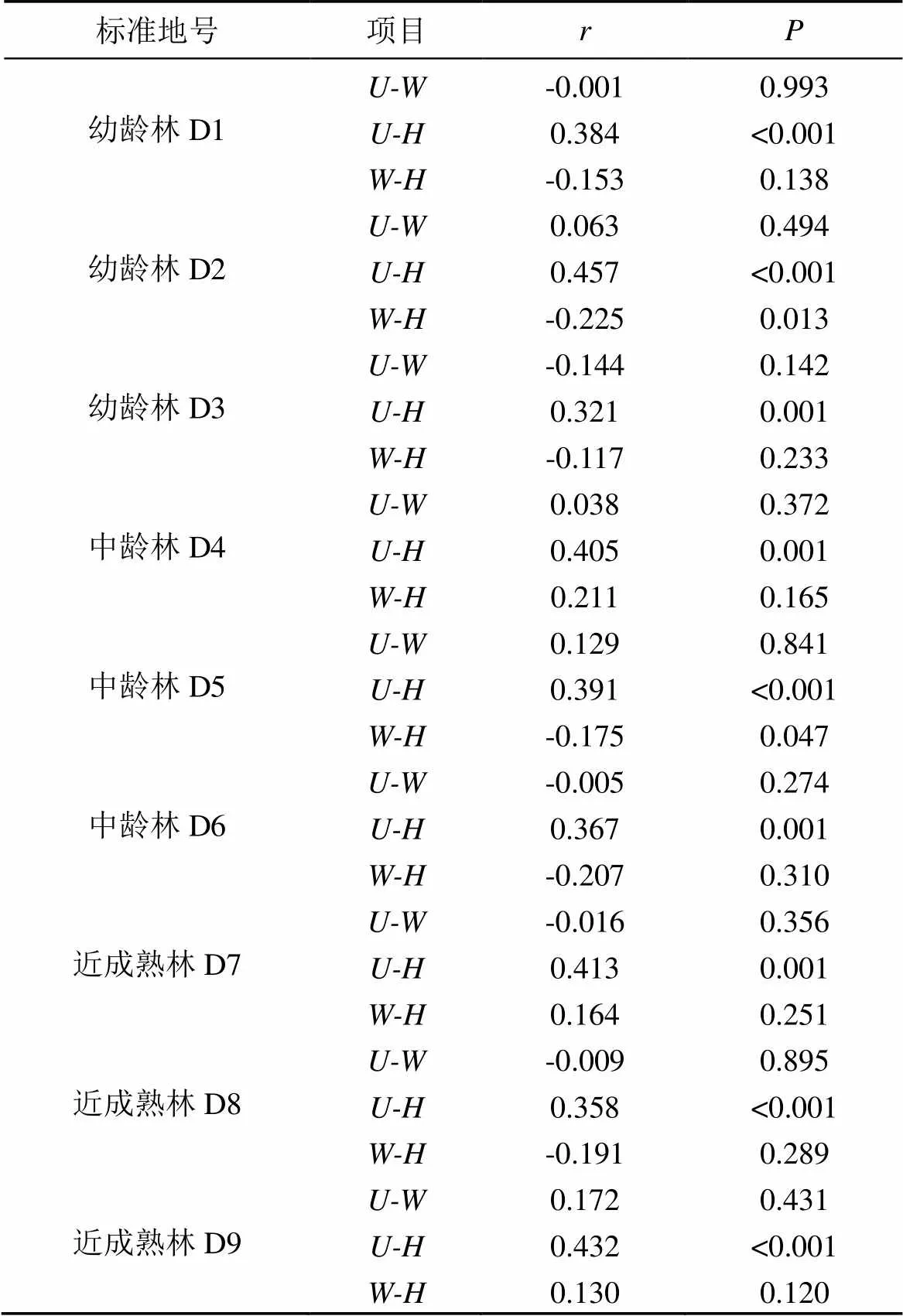
表2 空間結構參數相關性

3 討論

林分空間結構是林分功能的基礎和表現, 要優化林分的空間結構, 首先要分析現有林分結構的特點, 其次根據經營目標進行合理調整[23]。大小分化程度較低, 可以通過間伐補植進行改善。通過撫育間伐, 人為地促進自然更新, 可以調節林木個體的大小分化水平, 使林分徑級分布趨于合理, 促進林分的發育[24]。在調整過程中, 可以針對一些比較容易控制的參數進行優化, 例如涉及到距離的競爭指數不好調整, 但競爭指數與大小比數相關性高, 則可以調控林分的大小比數, 從而使競爭指數相應提高。對于兩個相關性較高的參數, 在調整時不一定都要考慮, 在條件有限的情況下, 可以適當地只調整一個參數。

曹小玉等用混交度、大小比數、角尺度、競爭指數、林層指數和開敞度等6個林分空間結構參數分析了杉木生態公益林的林分空間結構特征, 采用乘除法提出林分空間結構評價指數, 為杉木生態公益林理想空間結構的表達探索了一條新途徑[9], 但由于在指數提出過程中沒有考慮參數之間的相關性, 所以各參數所占的權重一致。本文基于此, 采用大小比數、角尺度和競爭指數分析人工杉木林的空間結構特征, 并分析空間結構參數之間的相關性, 以期在計算林分空間結構評價指數時, 為各參數權重的確定提供指導。此外, 林分空間結構不僅受林木自生生長的影響, 還受坡位、坡度、坡向、土壤養分等多方面環境因素的綜合影響, 關于這些因素對林分空間結構的影響的研究還有待進一步開展。

4 結論

本文通過計算人工杉木林的三個林分空間結構參數: 大小比數、角尺度、競爭指數, 分析了杉木人工林的現有林分空間結構。結果表明: 杉木各齡級的大小比數都接近中庸狀態, 林木分化不嚴重。空間分布處于均勻和隨機的中間狀態, 經過天然更新和適當的人為調整, 能夠較為容易地達到隨機分布的狀態。平均競爭指數在三個齡級之間呈極小幅度的波動, 說明林木之間的競爭并不會隨著年齡的增長而變大或減小。并利用SPSS軟件對這三個參數之間進行相關性分析, 得出三個參數之間的相關性, 為空間結構優化經營措施提供依據。結果顯示: 角尺度和大小比數、競爭指數之間沒有相關性, 即角尺度具有獨立性, 在林分空間結構評價指數的計算中所占的權重應相對較大。而大小比數和競爭指數之間呈中度相關的關系, 兩個參數均能夠在一定程度上描述林木的空間競爭優勢, 所以二者在空間結構評價指數中所占的權重應適當減小。在實際的應用中, 角尺度作為一個獨立參數, 一定要考慮。而大小比數和競爭指數可以根據實際的樣地情況, 調查研究目的, 選擇其中一個。大小比數的獲取更加容易, 因此如果在樣本總量龐大的時候, 可以用其進行計算。而如果想要獲取更為準確的競爭關系, 考慮林木單木位置的競爭指數則更加準確。還可以通過研究這兩個參數之間的具體相關關系, 提出一個新的參數, 綜合考慮兩者的影響。

[1] 尹惠妍, 張志偉, 蘇衛靜, 等. 八一鎮濕地公園林分空間結構分析[J]. 西北林學院學報, 2019, 34(3): 149–153.

[2] 張會儒. 東北天然林可持續經營技術研究[M]. 北京: 中國林業出版社, 2011.

[3] 惠剛盈. 基于相鄰木關系的林分空間結構參數應用研究[J]. 北京林業大學學報, 2013, 35(4): 1–9.

[4] 胡剛, 張忠華, 程安云, 等. 黔中天龍山喀斯特次生林林分空間結構的量化與分析[J]. 地球與環境, 2017, 45(1): 25–31.

[5] 張今朝, 劉健, 余坤勇, 等. 福建陳大國有林場生態公益林林分結構特征及優化調整[J]. 西南林業大學學報:自然科學, 2017, 37(4): 132–139.

[6] 王智勇, 董希斌, 張甜, 等. 大興安嶺落葉松天然次生林林分結構特征[J]. 東北林業大學學報, 2018, 46(4): 6–11.

[7] 董靈波, 劉兆剛. 樟子松人工林空間結構優化及可視化模擬[J]. 林業科學, 2012, 48(10): 77–85.

[8] 張崗崗, 劉瑞紅, 惠剛盈, 等. 林分空間結構參數N元分布及其詮釋——以小隴山銳齒櫟天然混交林為例[J]. 北京林業大學學報, 2019, 41(4): 21–31.

[9] 曹小玉, 李際平, 封堯, 等. 杉木生態公益林林分空間結構分析及評價[J]. 林業科學, 2015, 51(7): 37–48.

[10] 曹小玉, 李際平. 林分空間結構指標研究進展[J]. 林業資源管理, 2016(4): 65–73.

[11] 弓文艷, 陳麗華, 余新曉, 等. 遼東大伙房水庫庫區天然針闊次生林林分空間結構[J]. 生態學雜志, 2018, 37(11): 3255–3261.

[12] 惠剛盈, GADOW K V, 胡艷波. 林分空間結構參數角尺度的標準角選擇[J]. 林業科學研究, 2004(6): 687–692.

[13] 李際平, 房曉娜, 封堯, 等. 基于加權Voronoi圖的林木競爭指數[J]. 北京林業大學學報, 2015, 37(3): 61–68.

[14] 曹小玉, 李際平, 封堯. 福壽林場馬尾松生態公益林林分空間結構研究[J]. 林業資源管理, 2014(3): 45–50.

[15] 孔雷, 亢新剛, 楊華, 等.長白山楊樺次生林樹種空間隔離度對林分生長的關系[J].中南林業科技大學學報, 2012, 32(7): 14–18.

[16] 康希睿, 李曉剛, 張涵丹, 等. 不同混交措施下杉木人工林群落穩定性特征[J]. 生態學雜志, 2020, 39(9): 2912– 2920.

[17] 石振威, 曾思齊, 劉發林, 等. 基于地形與競爭因子的青岡櫟次生林樹高啞變量模型研究[J]. 西北林學院學報, 2020, 35(1): 196–202+272.

[18] 毛沂新, 張慧東, 王睿照, 等. 遼東山區原始闊葉紅松林主要樹種空間結構特征[J]. 應用生態學報, 2019, 30(9): 2933–2940.

[19] DAVIES O, POMMERENING A. The contribution of structural indices to the modeling of Sitka spruce and birch crowns[J]. Forest Ecology and Management, 2008, 256: 68–77.

[20] POMMERENING A. Evaluating structural indices by reversing forest structural analysis[J]. Forest Ecology and Management, 2006, 224(3): 266–277.

[21] 唐楊, 陳紅, 童躍偉, 等.長白山闊葉紅松林不同強度擇伐后關鍵樹種的競爭關系[J]. 應用生態學報, 2019, 30(5): 1469–1478.

[22] 范春雨, 張春雨, 趙秀海. 擇伐對吉林蛟河闊葉紅松林群落結構及動態的影響[J]. 生態學報, 2017, 37(20): 6668– 6678.

[23] 張君鈺, 楊培華, 李衛忠, 等. 油松林林分空間結構分析及評價指數構建[J]. 西北林學院學報, 2020, 35(5): 166– 172.

[24] 曹小玉, 李際平, 胡園杰, 等. 杉木生態林林分間伐空間結構優化模型[J]. 生態學雜志, 2017, 36(4): 1134–1141.

Analysis and correlation study on spatial structure parameters of artificialforest stand

LAI Minhua1, LAI Riwen1, *, HU Renjie1, YE Wei2

1. School of Forest, Fujian Agriculture and Forestry University, Fuzhou 350002, China 2. Fujian Forestry Investigation and Design Institute, Fuzhou 350002, China

Based on the measured data of nine artificialforest standard plots in Songxi Forest Farm of Nanping City, the spatial structure parameters offorest stand were evaluated and analyzed, which laid the foundation for the formulation of spatial structure optimization and adjustment measures offorest and other pure forest stands. Neighbor trees of the object one was determined based on n = 4. Three stand spatial structure parameters of neighborhood comparison, uniform angle index and competition index were used to analyze their spatial structure characteristics. The result shows that the neighborhood comparison of theforests in the nine standard plots are close to the mean state, the individual differences of the trees are not large, and the differentiation of the trees is not serious; the uniform angle index is between uniform and random distribution, and there is a certain gap from the ideal model of horizontal distribution; the competition index is relatively stable, and there have been no significant changes due to age. The relationship between the neighborhood comparison and the competition index is moderately correlated, while the correlation between the neighborhood comparison and the uniform angle index, and the uniform angle index and the competition index are almost nonexistent. The results are helpful to the sustainable management of artificialforest.

; neighborhood comparison; uniform angle index; competition index; correlation

賴敏華, 賴日文, 胡仁杰, 等. 人工杉木林林分空間結構參數分析及相關性研究[J]. 生態科學, 2021, 40(3): 58–63.

LAI Minhua, LAI Riwen, HU Renjie, et al. Analysis and correlation study on spatial structure parameters of artificialforest stand[J]. Ecological Science, 2021, 40(3): 58–63

10.14108/j.cnki.1008-8873.2021.03.008

S757.3

A

1008-8873(2021)03-058-06

2020-08-15;

2020-10-16

福建農林大學科技創新基金項目(KFA17284A); 林學高峰學科建設項目(71201800755)

賴敏華(1995—), 女, 碩士研究生, 主要從事森林經理學, 3S研究, E-mail: 757345331@qq.com

賴日文, 男, 博士, 副教授, 主要從事森林經營管理和3S技術教學科研, E-mail: fjlrw@fafu.edu.cn