巧用數形結合 撬動思維支點

潘新花

數學是一門研究現實世界的空間形式和數量關系的學科，是研究數與形及其相互關系的一門科學。數形結合思想在數學教學中是一種重要的數學思想，小學生的思維以直觀形象思維為主，比較容易理解直觀模型，但是又要向抽象思維過渡，數形結合便是溝通學生形象思維和抽象思維的橋梁，它能促進學生形象思維和抽象思維的協調發展，通過形象思維和抽象思維的巧妙結合，可以優化課堂教學，使復雜問題簡單化，使抽象問題具體化。

一、數形結合，理解概念

數學概念是人腦對現實對象的數量關系和空間形式的本質特征的一種反應形式。在小學階段，學生無論是學習整數還是分數，小數，負數，都離不開幾何直觀的支持，利用幾何直觀可以將抽象的概念具體化，直觀化，讓學生更好地理解數學的概念。

例如，在教學“分數的初步認識”時，分數是比較抽象的數學概念，為了激起學生學習興趣，可以利用學生已有的生活經驗，合理地借助直觀圖形，將抽象的數學概念轉化為直觀、易懂的圖形概念。教學時，先喚起學生的生活經驗，讓學生借助實物，蘋果，月餅認識“一半”可以用分數1/2來表示，緊接著再利用各種幾何圖形，如正方形，長方形，圓形，數軸等圖形，理解分數1/2的意義，并啟發學生思考，為什么正方形、長方形、圓形、數軸這些圖形一直在變化，卻都還能找到同一個分數1/2？這樣借助圖形的演變，進一步使學生對分數概念的理解和把握越來越清晰，充實了學生對分數概念本質特征在思維中的建構。

二、數形結合，明晰算理

計算教學是小學數學教學中重要的組成部分，《義務教育數學課程標準（2011）》指出，學生不僅會用筆算、口算等進行正確的計算，還要結合具體的情境理解算理。學生學習數學需要有較多的動手操作和直觀表象作為支撐，借助幾何圖形，能夠幫助學生更加直觀地理解算理，讓學生自主發現、描述所要研究的問題，親歷知識產生、模型建構的過程，有效幫助學生理解算理，掌握算法。

例如，教學“兩位數乘兩位數”時，先出示例題“王老師，買了12套圖書，每套圖書有14本，一共買了多少本？”列式14×12=？這時引導學生用自己喜歡的方法算一算，并在點子圖（12行，14列）上把自己的想法表示出來。學生呈現了不同的口算方法，有的把點子圖12行平均分成二份，先算14×6=84，再算84×2=168;有的把點子圖上的12行平均分成三份，先算14×4=56再算56×3=168;也有的同學把點子圖上的12行拆成兩部分，第一部分10行，第二部分2行，先計算14×10=140，再算14×2=28，最后140+28=168。學生借助點子圖這一直觀的工具，在操作、交流、分析、比較中，明白了這些方法都是先分后合，把新的知識轉化為舊的知識來解決問題，同時為第二課時研究豎式計算方法做了鋪墊，在列豎式時，讓學生把每次相乘的結果都在點子圖上圈出來，這樣通過直觀的點子圖溝通了算法和算理的關系，幫助學生理解算理，掌握算法。

三、數形結合，拓寬思維

1.以形解數，解題策略多樣化

通過數形結合，以形解數，能夠幫助學生從多角度，多層次地思考問題，養成多向性思維的好習慣，引導學生變靜態思維方式為動態思維。

教學五年級上冊”圖形中的規律”一課時，教師首先引導學生獨立思考，由形思數，嘗試體驗圖形與數、圖形與算式之間的關聯，再讓學生從不同角度觀察劃分，發現同一個點陣存在著不同的規律。橫向縱向觀察時，算式6×6=62;斜向觀察時，算式1+2+3+4+5+4+3+2+1;折角觀察時，算式1+3+5+7+9。最后比較這些規律，讓學生在分析、比較、歸納中發現，從1開始幾個連續奇數相加，等于他們個數的平方;從1開始連續自然數相加，加到最大的數，再依次遞減，加到自然數1，所得的結果就是最大數的平方。

整個學習過程，學生自主交流，結合圖形與算式，發現規律，初次體驗“形”能夠直觀解釋“數”的計算，學會利用這一發現進行巧算，從而體驗成功的樂趣。

再如，教學五年級上冊“平面圖形的面積”進行相關知識點鞏固，如圖

2.借數思形，抽象推理具體化

教學中如果能夠找到數量背后的幾何圖形，借數思形，能夠幫助學生更形象直觀地發現規律，化繁為簡，化抽象為具體。

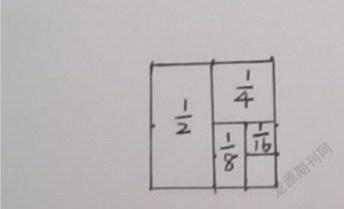
例如，在計算1/2+1/4+1/8+1/16+1/32+1/64+1/128=？，教師先引導學生借助圖形，從簡單的1/2+1/4入手，引導學生觀察發現，1/2+1/4可可以看成從正方形“1”中減去空白部分的1/4，1/2+1/4=1-1/4;同樣繼續借助圖形計算1/2+1/4+1/8，學生發現可以把剩下的1/4再平均分成兩份，每份是1/8，因此，1/2+1/4+1/8，可以看成從正方形“1”中減去1/8;那么同理1/2+1/4+1/8+1/16可以看成從正方形“1”中減去1/16。.以此類推，1/2+1/4+1/8+1/16+1/32+1/64+1/128=1--1/128=127/128。

3.數形邂逅，解題思路直觀化

學生在數學學習過程中，經常會遇到一些數量關系比較復雜的問題，利用圖形進行數學問題的思考，可以把“無形”的解題思路化為“有形”的圖形方法，從而拓寬解圖思路，找到解決問題的方向。

例如，把一個長方體木條分割成大小相等的5個小正方體后，表面積之和增加了80平方厘米，原來這個長方體的表面積是多少平方厘米？這道練習題對兩個班級的學生進行了測試，其中一個班級的試題中附加了一個條件，要求畫出草圖，結果發現有畫草圖的這個班級作答正確率遠高于沒要求畫草圖的班級。孩子根據題目中提供的數學信息畫出草圖后，會發現長方體分割成5個大小一樣的小正方體后，表面積增加了8個面，正好是40平方厘米，所以每一個面的面積是5平方厘米，而長方體的表面積未分割前有22個面，因此原來長方體的表面積就是22×5=110平方厘米。可見，畫圖對于幫助解決較為抽象的數學問題，起到化抽象為具體的作用。

總之，通過數與形的相互轉換，以形助數，以數輔形，數形相輔相成，將抽象的數學語言與直觀的圖形結合起來解決問題，讓學生主動經歷知識的形成過程，促使學生數學核心素養得到培養，思維能力得到提升。