靜強度/耐久性初步結構優化設計方法

常楠,徐榮欣,陳先民,楊軍,李毅

1.成都飛機設計研究所,成都 610091

2.中國飛機強度研究所,西安 710065

3.西北工業大學 航空學院,西安 710072

在經典的設計流程中,耐久性設計分析工作是在詳細結構設計完成后開始的,如果結構的疲勞壽命沒有達到設計要求,工作流程將返回結構設計專業,更改結構細節設計(比如孔徑、導角半徑等),在某些嚴重情況下,還需要對各部件上的載荷進行調整,對各部件的截面尺寸進行更改,此時,迭代設計所影響到的范圍將擴大,若將迭代設計視為一個閉環,此時閉環的直徑將覆蓋至初步結構設計階段。顯然,迭代閉環的直徑越大,所消耗的設計資源也就越多,這是設計師所不愿看到的。若能在結構初步設計階段就對耐久性約束加以考慮,將可以有效地避免大范圍的迭代設計工作。但是,初步結構設計中僅對各部件在不同站位處的截面尺寸進行了設計,還未確定疲勞分析所需的結構細節幾何尺寸,有限元模型的精度也較低；載荷方面,結構初步設計中采用的設計載荷工況數目很少,僅覆蓋了各部件的極限載荷情況,無法完整地描述飛機整個服役期內的載荷歷程,所以在結構初步設計階段中難于對耐久性這一重要設計約束加以考慮。

另一方面,在飛機設計過程中,模型的精度是逐漸提高的,從最初的基于以往數據的統計模型(各部件的結構重量估算公式[1]),然后發展到以梁單元為主的梁架模型,再到采用板、桿、梁單元的總體有限元模型,最后發展為包含連接單元、三維實體單元的細節結構有限元模型。隨著模型精度的變化,響應的種類也從的應力和變形,增加到臨界屈曲系數、振動頻率、臨界顫振速度、發散速壓、操縱面效率和疲勞壽命等多種與結構設計密切相關的響應數據。以這些豐富的響應數據為基礎,便可以在結構設計中引入不同的設計約束。可見,結構設計約束的種類和數目依賴于所采用模型的精度。

本文算例中的折疊機翼相對于常規機翼來說,外翼載荷通過連接結構傳遞到內翼結構中,在連接結構上產生較大的集中載荷,連接結構中負責集中載荷傳遞的接頭耳片也隨之成為了疲勞關鍵部位,并且由于高載荷的作用,內外翼連接結構為了達到強度和剛度的要求,需要分布更多的材料,所以其結構重量占整個機翼重量的比例高于常規機翼中的加強肋。可見,折疊機翼輕量化設計的一個關鍵點是：內外翼連接結構是否能夠以較輕的結構重量來同時滿足靜強度和耐久性兩方面的要求。本文將折疊翼連接結構(耳片)耐久性設計與分析提前到折疊機翼的初步結構設計中,在結構選型與布置中就對連接耳片中的應力進行控制,通過多工況優化設計,使其在滿足靜強度和耐久性要求的前提下,達到輕量化設計的目標。

因此,本文將從結構變精度模型的建模技術出發,研究在初步結構設計中開展耐久性分析的途徑,建立綜合靜強度與耐久性約束的初步結構優化設計方法,將耐久性設計與分析環節提前到結構初步設計階段,提早考慮結構的耐久性指標,降低發生大范圍迭代設計的概率,提高結構設計工作的效率。相比僅能更改孔徑和導角半徑等細節幾何尺寸的細節結構抗疲勞設計,在初步結構設計中可以通過改變各部件的截面尺寸,來調整各部件上承擔的載荷,因此具有更大的設計空間,從而實現結構輕量化設計的機會也更大。

雷神飛機公司的高級工程師Robert和普渡大學Terrence教授的研究指明在飛機設計過程中,結構有限元模型是逐漸進化的,其精度也是不斷提高的[2]。他們以一典型的亞聲速噴氣客機機翼結構為例子,建立了三代有限元模型,開展了設計分析,其中在第三代有限元模型中采用了子結構和子模型技術來進一步豐富結構的細節信息。洛克希德公司在F-35先進戰斗機的結構設計中,采用了2.5D有限元建模技術,建立加強框和平尾連接結構等關鍵部位的2.5D模型,模型中用殼單元對連接耳片,框腹板上的加強筋,減輕孔邊的緣條的幾何外形進行了模擬[3]。國內王想生等采用子結構技術提高了機翼主梁結構有限元模型的精度[4]。

在耐久性優化設計方面,國內南京航空航天大學的薛彩軍等提出了基于響應面模型的結構疲勞壽命優化方法,并對某飛機起落架的撐桿進行了抗疲勞優化設計[5]。航空工業哈爾濱飛機工業集團有限責任公司的劉志芳等利用Miner線性損傷累積理論,將疲勞壽命設計要求轉化為了應力約束,對機翼典型高應力開口區進行了抗疲勞優化設計[6]。南京航空航天大學的陳濱琦等提出了基于有限元分析的細節疲勞額定值(DFR)疲勞可靠性分析方法,并利用此方法對某型飛機作動筒支座開展了抗疲勞優化設計[7]。

從上述研究現狀可以看出,變精度結構有限元模型和2.5D有限元建模技術是目前和未來飛機設計中的熱點研究技術,國內缺乏這方面的研究工作；在抗疲勞優化設計方面,已有的研究都是針對局部結構開展的,也處于詳細結構設計階段的后期,未將耐久性設計提前到初步結構設計階段。本文針對上述2個領域開展研究工作,首先對變精度模型技術進行研究,然后對細節疲勞額定值方法的基本理論進行解析,確定與初步結構設計進行數據交換的途徑,在上述兩方面研究的基礎上,建立靜強度與耐久性綜合約束下的初步結構設計方法,然后將所發展的方法應用到折疊機翼初步結構設計中,并實現了輕量化設計。

1 理論與方法

1.1 變精度模型

隨著結構設計工作的向前推進,結構工程師所采用的模型精度也是逐漸提高的,同時結構響應和設計約束也是不斷增多的,如圖1所示。最初,結構工程師采用基于已有飛機數據的統計模型[1]對飛機各部件的結構重量進行估算。然后,用桿、梁和殼單元建立起能夠描述結構型式、結構布置和結構截面尺寸分布的2D(2維)有限元模型,通過插值算法(比如徑向基函數)將載荷專業提供的氣動載荷分配到結構有限元節點上,氣動載荷可以由低精度的渦格法、中精度的面元法和高精度的CFD或風洞試驗獲得。系統設備、發動機和燃油的質量可以通過集中質量單元模擬,并用多點約束單元連接到支撐結構上。通過有限元靜力計算獲取結構中的應力和變形響應,以這些響應數據為基礎,并借助強度和穩定性理論來建立靜強度、剛度和穩定性設計約束。將此階段的結構有限元模型與平板氣動力模型(渦格法)耦合可建立氣動彈性模型,開展靜/動氣動彈性計算,獲取結構固有振動頻率和振型、臨界顫振速度、發散速壓、操縱面效率,據此建立動強度和靜氣動彈性設計約束,由于靜氣動彈性分析中也可以獲得應力和變形響應,因此我們也可以建立靜強度和剛度約束。

本文為了在飛機初步結構設計中增加耐久性設計約束,以變精度模型概念為指導,用2.5D(2.5維)有限元建模技術對傳統飛機結構總體有限元模型(2D有限元模型)的精度進行了改進。在2D有限元模型的基礎上,用殼單元來對以往用桿、梁單元模擬的結構進行更精細的建模,通過增加連接單元數目和采用新型連接單元(比如ABAQUS軟件中的Ti單元),來模擬各結構零件的連接,代替以往“共節點”的方式,對飛機結構進行更準確的幾何描述,比如：減輕孔、連接螺栓孔等,進而建立起飛機結構的2.5D有限元模型,這種有限元模型中具有更豐富的幾何信息,這為耐久性分析工作的展開提供了必要的條件。最近,美國在F-35飛機的設計中,建立了關鍵部件的2.5D 有限元模型[3],這些2.5D有限元模型不但可以實現2D有限元模型中的所有設計約束,而且其獲取的應力和變形響應更精確,可以減少細節結構有限元建模與分析的工作量。為子結構,子模型技術的應用提供了更準確的幾何邊界。由于可以對連接件、減輕孔等細節進行建模,所以可以獲得與真實結構更接近的重量數據。另一方面,在2.5D有限元模型中,對全部蒙皮進行了模擬,并且單元尺寸更小,這對高精度氣動載荷的施加也是十分有利的。

1.2 安全裕度

在結構設計中可通過安全裕度[8](Margin of Safety,MS)來描述結構的靜強度安全情況,當MS≥0時,認為結構滿足靜強度要求,當MS<0時,認為結構不滿足靜強度要求,需對結構幾何尺寸進行改進。MS的計算公式為

(1)

式中：[σ]為結構材料的許用值,可取為材料的屈服應力;σ為設計載荷作用下結構工作應力,可以通過飛機結構2D有限元模型或2.5D有限元模型開展線性/非線性計算獲得。

1.3 細節疲勞額定值(DFR)與疲勞裕度

細節疲勞額定值(DFR)是結構細節本身固有的疲勞性能特征值,是一種對構件質量和耐重復載荷能力的度量[9]。該值是當應力比R=0.06時,結構細節壽命具有95%置信度和95%可靠度,能夠達到105次循環壽命的最大應力(MPa)。采用DFR方法對飛機結構進行疲勞分析的步驟[10]可如下：

1)確定當量等幅載荷和目標壽命對應的當量等幅載荷循環數

依據指定機種的隨機疲勞載荷譜(重心過載譜)當量等幅值化后[10],通過全機有限元求解獲取指定部位的當量等幅載荷σmax,并確定每飛行小時對應的當量等幅載荷循環數Nfh。

若指定機種的目標壽命為Tg,則目標壽命對應的當量等幅載荷循環數Ne為

Ne=FRF·Tg·Nfh

(2)

式中：FRF為疲勞可靠性系數,對軍用飛機而言,由于機體結構均強調按耐久性/損傷容限準則加以設計,大部分結構不必再考慮疲勞可靠性系數,只是對于按安全壽命準則設計的起落架和一些特殊結構,FRF取值為1.5。

2)確定結構的細節疲勞額定值的許用值[DFR]

選取相似結構的DFR作為細節疲勞額定值的基準值DFRbase,并根據實際結構的材料、結構型式、加工制造工藝、裝配工藝等因素進行修正后獲得[DFR],這里本文以受拉耳片為例給出[DFR]的計算公式[9],以配合本文中的算例。

[DFR]=DFRbase·K·B·Lt·Ld·Ls·Lθ·RC

(3)

式中：K為材料參數,對于鋁合金取1.0,對于鈦合金取1.6,對于高強度鋼(σb>1 655 MPa)取1.9,對于中等強度鋼(σb≤1 655 MPa)取2.2；B為合金和表面處理系數；Lt為耳片厚度系數；Ld為尺寸(孔徑)系數；Ls為形狀系數；Lθ為斜載荷系數；RC為構件疲勞額定系數。

3)計算當量等幅載荷對應的許用應力[σmax]

當量等幅載荷對應的許用應力[σmax]是指定應力比下,具體結構部位([DFR]已確定)的疲勞壽命能夠達到目標壽命所對應的當量等幅載荷循環數時所允許的最大應力值。可由式(4)獲得[10]。

[σmax]=

(4)

式中：r為應力比；對于民機,N0=1×105,對于軍機,Ne=5×104；σm0為等壽命曲線參數；m為S-N曲線斜率參數。

4)計算疲勞裕度

疲勞裕度的計算公式[10]為

(5)

若疲勞裕度為負,說明疲勞壽命不達標,須減小使用應力,同時(或者)通過改進細節設計,增加其DFR,使疲勞裕度等于或大于零,進而達到目標壽命。期間應該注意到,為了減小使用應力而改變結構幾何尺寸時,會引起DFR的變化,這在優化設計中需特別注意。因為在優化迭代計算中優化變量(結構幾何尺寸)的改變會引起DFR的變化,進而改變優化設計約束MF,迭代計算中必須進行實時更新。

1.4 靜強度與耐久性綜合約束下的機翼初步結構優化設計方法

在初步結結構優化設計中,各結構件沿航向、展向和弦向的截面尺寸是變化的,可以通過不同的獨立設計變量來描述,并建立2D/2.5D有限元模型(FEM),施加設計載荷,開展靜力有限元計算獲取結構的應力和變形響應,并與材料的屈服強度和結構的許可變形進行比較運算后建立強度和剛度優化約束；并輸出結構重量,設定其最輕為優化目標。

同時,在2D/2.5D有限元模型(FEM)上施加當量等幅譜峰值對應的載荷工況,開展靜力有限元計算獲取結構的應力響應,將此結構應力響應與當量等幅載荷對應的許用應力[σmax]進行比較后獲得疲勞裕度MF,便可以建立耐久性優化設計約束(疲勞裕度大于零)。期間需要注意的是,在優化迭代計算中,結構幾何尺寸的更新會引起結構的細節疲勞額定值許用值[DFR]的改變,進而改變許用應力[σmax]和疲勞裕度MF,因此在初步結構優化計算中耐久性優化約束是變化的,需要對其進行實時更新。

將上述2個載荷工況綜合后,按圖2中的流程建立多工況優化設計問題,便可以在初步結構設計中增加耐久性設計約束,從而將耐久性設計環節提前至結構設計的初期,實現靜強度與耐久性綜合約束下的初步結構優化設計。

圖2 靜強度與耐久性綜合約束下的初步結構優化設計流程

2 折疊機翼初步結構設計

本文以一折疊機翼的初步結構設計為例來說明靜強度與耐久性綜合約束下的初步結構優化設計方法。

2.1 設計對象與結構布置

機翼為小展弦比后掠機翼,沿展向分為內外2個部分(內翼和外翼),內外翼通過順航向布置的轉軸和接頭進行連接。沿升力方向的設計過載為nz,可采用的材料有鋁合金和鈦合金,材料性能如表1所示,對其開展初步結構設計,在滿足靜強度和翼尖升力方向變形不超過5%b(b為半展長)的要求下,對內外翼的結構布置和各結構件沿展向/弦向的截面尺寸進行設計；對于內外翼連接接頭,除了需要考慮靜強度和翼尖變形約束外,還需考慮耐久性約束,在滿足這些設計約束下對接頭厚度進行設計。

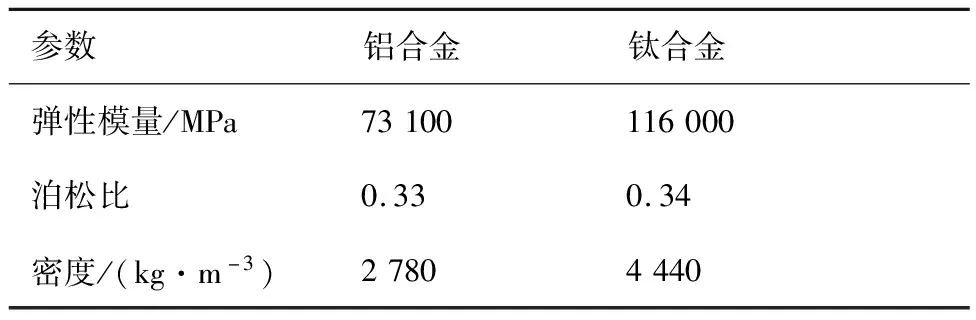
表1 材料性能參數

為了滿足上述設計要求,在內翼布置5根梁,其中前后梁通過單耳與機身結構連接,前后梁之間有3根較強的梁通過雙耳與機身結構連接；在外翼布置4根梁。沿展向布置7根肋,其中內外翼連接處為加強肋；內外翼通過靠近前后梁的兩組接頭連接,每組接頭由多個雙耳組成(內翼4個,外翼3個),內外翼的耳片都連接到順航向布置的轉軸上。

2.2 分析模型與方法

步驟1建立2D有限元模型。本文用梁單元模擬梁緣條,梁單元截面形狀為矩形,其長和寬分為優化設計變量；用桿單元模擬肋緣條,桿單元的截面積為設計變量；用殼單元模擬蒙皮和腹板,殼單元的厚度為優化設計變量。結構沿展向分為5區,如圖3所示,每個區內的蒙皮厚度用不同的優化設計變量表示,區域內的梁緣條和腹板也是如此；每個肋的緣條和腹板厚度也用不同的設計變量描述。

圖3 機翼展向分區

步驟2以2D有限元模型為基礎開展全局優化設計,確定內外翼各結構件的截面尺寸,并提取內外翼連接耳片上的集中載荷。將接頭耳片分為4組,如圖4所示,每組耳片的厚度和主要幾何尺寸(x,y)都是相同的,依據此組中最大的集中載荷P來確定,首先根據連接螺栓的剪切強度(式(6))來確定銷釘和耳片孔的直徑D,再根據耳片的受拉強度(式(7)),來對耳片的主要幾何形狀(x,y)和厚度t進行設計(由于在設計初期,所以近似按受軸向拉伸的直耳片處理，如圖5所示)。

圖4 2D有限元模型

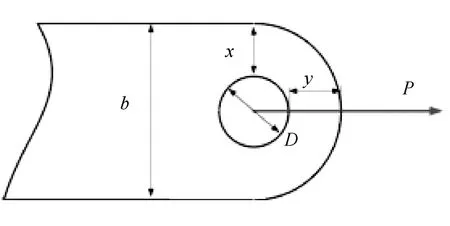
圖5 受軸向拉伸載荷的耳片

(6)

式中：τb為螺栓材料的剪切強度。

(7)

式中：σult為按垂直耳片軸線凈面積設計的(極限)拉伸應力;F為沿孔中心的凈面積,單耳：F=(b-D)t,K′0為耳片受軸向拉伸載荷時的形狀系數(可查閱飛機設計手冊[8]);m0為受軸向拉伸載荷時的耳片材料系數(可查閱飛機設計手冊[8])。

(8)

式中:P取用每組耳片中的最大集中載荷,所計算獲得的σref可作為疲勞裕度計算(式(5))中的σmax。

步驟3根據所確定的耳片主要幾何尺寸與厚度建立內外翼連接耳片(含肋)的2.5D有限元模型(如圖6所示),在2.5D有限元模型中,用殼單元模擬肋的緣條、腹板和耳片接頭,用不同厚度的殼單元來描述結構材料的分布。用ABAQUS軟件中的Tie單元將不同網格密度的蒙皮和肋緣條進行連接,接頭與轉軸間通過多點約束單元進行連接,從而形成2D/局部2.5D混合有限元模型,如圖7所示。將耳片厚度設為優化變量(如圖6所示,每組耳片用3個獨立設計變量(T1～T3)來描述其厚度分布),采用1.4節中建立的方法,以《民機結構耐久性與損傷容限設計手冊(上冊)》[8]中的數據曲線為基礎,便可建立優化設計變量(耳片厚度Tlug)與幾何修正系數Lt之間的對應關系,同時也可根據耳片的主要幾何尺寸和載荷方向進一步確定式(3)中的其他系數和變量,從而計算出[DFR],并進一步由式(4)獲得[σmax],然后再提取接頭上的集中載荷P,根據式(7)計算出σmax,最終利用式(5)計算出疲勞裕度MF,建立MF大于零的不等式,將其作為耐久性約束。聯合設計載荷工況,并設定對應的靜強度約束,開展多工況局部優化設計,流程如圖8所示。可以在Isight和ABAQUS軟件環境實現多工況優化問題(設計工況與當量等幅譜峰值對應的載荷工況,上述2種載荷工況可以由載荷設計專業獲得,這里不再詳述),如圖9所示。

圖6 耳片與肋的2.5D有限元模型，局部優化中的設計變量

圖9 Isight中的優化框圖

為了配合設計流程圖,表2對優化問題進行了總結。全局優化中只有一種載荷工況：設計載荷工況,通過結構中米塞斯應力σvm小于材料的屈服強度σs來定義優化中的靜強度約束,通過翼尖升力方向變形量Dtip小于機翼半展長b的5%來定義優化中的剛度約束；依據全局優化的結果,對機翼結構幾何尺寸進行更新,建立2D/局部2.5D 有限元模型,開展局部優化設計,在局部優化中有2種載荷工況,載荷工況1(case 1)為設計載荷工況,其對應的優化約束為靜強度和剛度約束,載荷工況2(case 2)為當量等幅譜峰值對應的載荷工況,其對應的優化約束為疲勞裕度(式(5)和式(8))計算)大于零,優化變量為每組耳片的厚度,優化目標為耳片結構重量最輕。

表2 優化問題

2.3 優化設計與分析

本文采用可行性方向法進行優化計算,經過迭代計算,機翼結構重量收斂于初始重量的51%,如圖10所示(其中W0為結構重量初始值,i代表迭代次數),由于對翼尖變形量的嚴格限制,全機結構米塞斯應力不超過231 MPa,變形和應力如圖11所示。以此為基礎建立2D/2.5D有限元模型,開展局部優化設計對耳片厚度進行優化,經過62次迭代計算后可知：在增加耐久性約束后,耳片的結構重量增加,其增量超過了初始重量的2%,如圖12所示。在初始設計值下,內翼A組耳片中的關鍵耳片(承受最大集中載荷的耳片)的疲勞裕度小于零,存在疲勞問題,經過多輪迭代計算后,各組耳片的疲勞裕度均超過了零,如圖13所示,滿足了耐久性設計要求。此時結構在設計工況作用下的變形和應力如圖13所示,在綜合考慮靜強度和耐久性約束的局部優化設計后,翼尖變形量與全局優化所確定的值一致(變化量小于4%的半展長),相對于全局優化中的2D有限元模型,局部優化中的2.5D有限元模型具有耳片的主要幾何特征,可以給出耳片孔邊應力,最大不超過500 MPa,小于鈦合金材料的疲勞極限,如圖14所示。

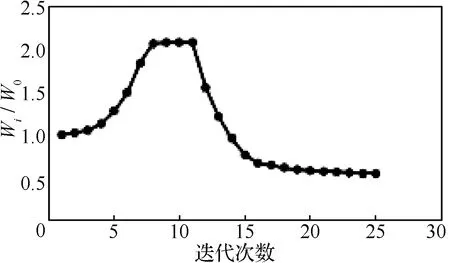
圖10 全局優化中的機翼結構重量迭代歷程

圖11 全局優化中的機翼結構應力與變形

圖12 局部優化中的耳片結構重量迭代歷程

圖13 疲勞裕度的迭代歷程

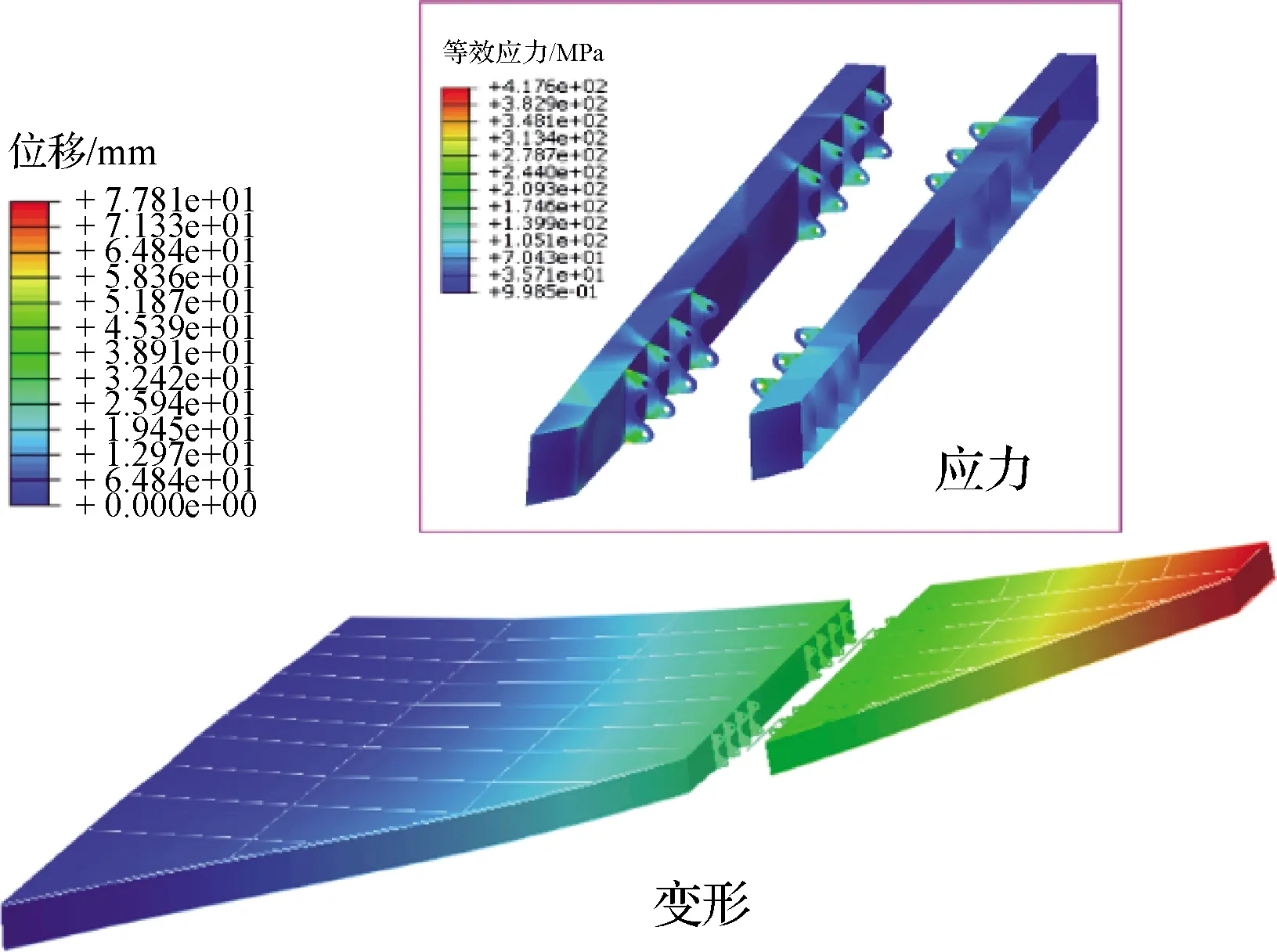
圖14 局部優化中的耳片結構應力與變形

在常規的設計流程與方法中,開展耐久性分析與設計之前,需要先進行初步結構設計和詳細結構設計工作,如圖15所示。在初步結構設計中,建立全機或部件的總體結構有限元模型(2D有限元模型),考慮強度和剛度設計約束,確定出各站位處的截面幾何尺寸和結構中的內載荷(比如：長桁上的拉壓載荷)；據此建立細節結構有限元模型,并開展細節結構設計,最終獲得足夠的幾何細節信息,為接下來的耐久性分析與設計提供輸入數據。當耐久性分析結果不滿足設計要求時,工作流程將返回至初步結構設計和細節結構設計階段,對結構進行修改,此時設計流程發生了大范圍的迭代,將消耗大量的設計資源。

然而,本文所發展的方法可以將初步結構設計、(部分)細節結構設計、耐久性分析與設計3方面的工作放到一個設計框架中并行開展,如圖2所示,也可以針對某一局部結構,以2D/局部2.5D 有限元建模技術為基礎,通過兩個階段的工作(全局優化和局部優化)來完成,比如文中的折疊機翼算例,設計流程如圖8所示。將3個流程圖(圖2,圖8和圖15)進行對比后可以發現,本文所發展的設計流程是明顯短于常規方法的,具有更高的設計效率。

圖15 常規結構設計流程

3 總結與展望

本文針對初步結構設計中難于開展耐久性分析的問題,以折疊機翼為研究對象,根據變精度模型技術,建立2D/局部2.5D有限元模型,以此模型提供的幾何設計變量和應力響應數據為橋梁,將疲勞設計細節疲勞額定值方法耦合到初步結構優化設計流程中,增加了耐久性設計約束,建立了靜強度與耐久性綜合約束下的初步結構設計方法。并對折疊機翼開展了全局到局部的優化計算,通過安全裕度和疲勞裕度兩個指標來實現對靜強度和耐久性約束的綜合考慮,經優化計算后,接頭耳片的疲勞裕度從初始值(內翼A組關鍵耳片,-0.15)提高到0.09以上,同時整個機翼結構在設計載荷工況下的安全裕度也大于零,所有耳片結構重量僅增加3%。最終以較小的結構重量代價獲得滿足靜強度和耐久性設計要求的折疊機翼/內外翼連接結構的初步結構設計。這說明：本文所發展的靜強度與耐久性綜合約束下的初步結構設計方法可以將耐久性分析與設計從詳細結構設計后期提前到初步結構設計階段,在結構選型與布置中就對結構中的應力進行控制,以滿足耐久性約束的要求,這樣可以減少詳細結構設計中由于疲勞壽命不足而引起的迭代設計次數,也增加了獲得更輕結構設計的機會。

另一方面,所發展方法中采用了變精度模型,隨著模型精度的提高,其強度、剛度和質量特性的信息越豐富,也越接近真實結構,這為開展不同專業分析提供了條件,比如：穩定性、振動、顫振和靜氣動彈性分析。因此可以在本文所發展的方法基礎上,增加耦合專業的數目,建立多學科優化設計,實現滿足多設計約束下的機體結構輕量化設計目標。