二階系統自抗擾控制的擴張狀態觀測器的改進

李承霖，孫洪飛

(廈門大學航空航天學院，福建 廈門 361102)

自抗擾控制技術(active disturbance rejection control,ADRC)是韓京清[1]先生提出的一種非線性控制方法，由跟蹤微分器、擴張狀態觀測器(extended state observer,ESO)和誤差反饋控制器組成.ADRC繼承了PID(proportional integral differential)“基于誤差來消除誤差”的思想，將被控對象中的各種擾動和不確定因素歸結為總擾動，然后在控制器中進行補償，從而將系統轉換為積分串聯的形式[2-3].它具有控制精度高、響應速度快、抗干擾能力強、對控制對象的模型依賴小等特點[4].為了減少調節參數、推廣ADRC的應用，GAO[5]在ADRC的基礎上提出了線性ADRC(LADRC)，并將待整定的參數與控制器和觀測器的帶寬聯系起來，從而將整定參數降低為3個，簡化了系統結構，極大地促進了其在工程上的應用.

作為LADRC最重要的結構，線性ESO(LESO)承擔著實時估計未知擾動的作用，從提出到現在，前人已經進行了大量細致的研究.Zheng等[6]分析了非線性時變系統LADRC的穩定性，并且證明當存在不確定性時，LESO跟蹤誤差是有界的.Xue等[7]分析了具有未知動力學和非連續擾動的不確定系統的自抗擾控制器性能.Zheng等[8]證明了具有不確定性n階系統的LESO跟蹤誤差是有界的，并且帶寬增加，誤差單調遞減.Huang等[9]采用自穩定區域(SSR)方法設計LESO，并分析了它的穩定性.Yang等[10]論證了LESO估計不確定性的能力，并進一步分析了LESO對正弦、方波、斜波等不同類型擾動的跟蹤能力.LADRC已經廣泛應用在工業電機控制[11]、電力控制系統[12]、軍事武器[13]、航空航天[14]、下肢康復訓練[15]等領域，其理論系統也更加完備.但目前研究主要關于LADRC的穩定性和LESO的收斂性及跟蹤誤差能力，未對LESO的暫態特性進行理論分析.文獻[5,16]中使用“帶寬”的思想，將極點統一配置到實軸上的一個具體位置，極大地減少了調節控制參數.該方法雖然也可以調節暫態性能，但是一定程度上縮小了LESO極點的取值范圍，減弱了調節暫態性能的靈活性，與具有非線性結構的ESO相比，跟蹤精度和響應速度受到制約，從而使暫態過程品質的提升受到限制.

為此，本文從暫態性能入手，沿用傳統LESO“帶寬法”的思想，通過加入兩個調節因子靈活調節觀測器的暫態性能和帶寬，并根據實際情況平衡二者的關系，以達到最佳的跟蹤效果.定量描述調節因子與暫態性能指標之間的關系，給出一般性結論，最大程度減少參數調節帶來的困難.最后將改進化的LESO(improved LESO,ILESO)與傳統的LESO做了仿真對比分析.

1 二階系統的ADRC模型回顧

考慮單輸入單輸出的二階系統

(1)

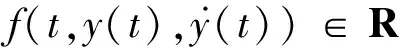
(2)

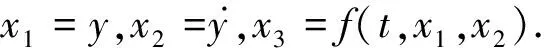
(3)

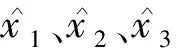
LLESO(s)=s3+β1s2+β2s+β3.

(4)

文獻[16]通過將觀測器的3個極點統一配置到左半實軸-ωo處，來確定觀測器增益矩陣.令

LLESO(s)=(s+ωo)3，

(5)

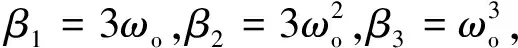
(6)

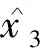
(7)

其中u0是虛擬控制量.將控制量u代入系統(1)可得

(8)

從而實現非線性系統補償之后的線性化.系統(1)轉化為積分串聯形式，進一步選取

(9)

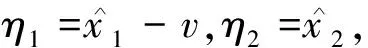
(10)

適當選取參數β01和β02，可以保證系統輸出漸近跟蹤輸入信號.顯然，控制器(6)的特征方程如下：

C(s)=s2+β02s+β01.

(11)

文獻[16]通過將控制器的2個極點配置到左半實軸-ωc處，來確定控制器狀態反饋系數.即令

C(s)=(s+ωc)2，

(12)

得到狀態反饋系數為

(13)

再次削減了調節參數的數量，其中ωc為控制器的帶寬.

綜上所述，在不考慮跟蹤微分器時，式(3)、(7)和(9)共同構成了LADRC[16].

2 改進型線性擴張狀態觀測器

2.1 ILESO的形式

文獻[5,16]中的LESO將極點統一配置到實軸上的一個具體位置，雖然也可以調節系統的暫態性能，但是減弱了調節暫態性能的靈活性，一定程度上制約了跟蹤精度和響應速度，必然使暫態過程品質的提升受到限制.ILESO在此基礎上額外給兩個參數β2和β3各乘上一個調節因子，便可以靈活改變極點的位置，從而改進觀測器的暫態性能.

對比傳統LESO的表達式(3)，給出三階ILESO的方程如下：

(14)

根據式(5)，ILESO的增益矩陣更新為

(15)

對式(14)進行拉氏變換可得

(16)

其中LILESO(s)是ILESO的特征方程，具體為

LILESO(s)=s3+β1s2+θβ2s+λβ3.

(17)

2.2 配置ILESO的主導極點

對系統式(1)進行拉氏變換：

s2Y(s)=F(s)+b0U(s).

(18)

(19)

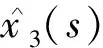
(20)

在實際情況中，一般使調節因子θ滿足如下條件：

(21)

根據一元三次方程的盛金判別法[18]可以證明，當滿足式(21)時，Ψ(s)的特征方程L*(s)=0有1個實根和2個共軛復根.在滿足穩定性的條件下，它們均位于s平面左半部分.假設實根為-ra，共軛復根為-a+bi、-a-bi，其中a、b、r均為正數，i為虛數單位.因此傳遞函數式(20)可以重寫為如下形式：

Ψ(s)=(λβ3)·{[s-(-ra)][s-(-a+bi)]

[s-(-a-bi)]}-1.

(22)

根據一元三次方程根與系數的關系以及LESO增益矩陣式(6)可得

(2+r)a=β1=3ωo,

(23)

(24)

(25)

根據式(23)～(25)可以進一步推出如下關系：

3a2-2β1a+θβ2=b2,

(26)

(27)

rθβ1β2(2+r)2-2r2β13-λβ3(2+r)3=0,

(28)

(β1-2a)(a2+b2)-λβ3=0.

(29)

為了簡化分析和加快系統響應速度，利用“主導極點”的思想，令實數極點遠離虛軸，使參數r滿足如下條件：

r>3.

(30)

將式(28)變換為如下形式：

(31)

在式(30)的約束下，由式(31)可以推導出此時調節因子θ和λ必須滿足如下關系：

(32)

根據高階系統的時域分析法[19]，舍掉非主導極點部分，式(22)中傳遞函數Ψ(s)可以近似為二階系統，重新配置增益，將其變換為如下形式：

(33)

系統阻尼比

(34)

顯然，此時ψ(s)為二階欠阻尼系統.

2.3 調節因子取值范圍

根據古典控制理論中的勞斯判據，列出式(17)LILESO(s)的勞斯列表(表1).

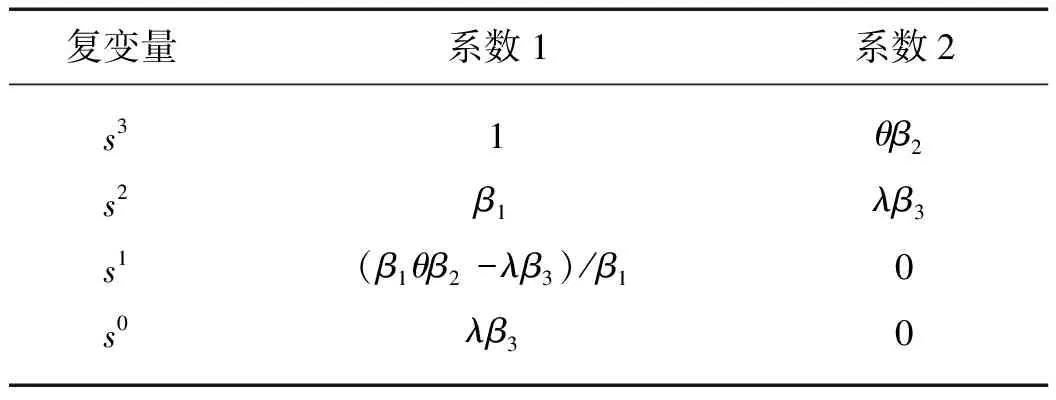
表1 ILESO特征方程的勞斯列表Tab.1 The Routh-Hurwitz table ofILESO’s characteristic equation

為了保證系統穩定性，調節因子需滿足下列條件：

(35)

綜合增益矩陣式(6)和2.2中的式(21)、(30)和(32)，可得ILESO調節因子θ和λ的取值范圍如下：

(36)

值得注意的是，引入“主導極點”的思想是為了便于簡化分析.在工程中可以放寬式(30)和(32)的約束要求，根據控制精度要求和抑制高頻擾動的帶寬要求，按照實時仿真的結果，靈活改變調節因子的取值，以達到最佳控制效果.

在工程實際操作中，可以先設置θ=1,λ=1，大致調節(粗調)ωo，使觀測器性能達到一個相對合理的程度，然后根據式(36)的調節因子取值范圍適當微調(精細調節)θ和λ的取值，從而達到進一步改進觀測器性能的目的.

3 ILESO的跟蹤誤差

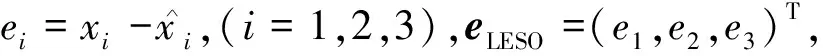
(37)

(38)

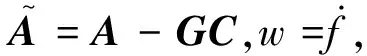
E×w(τ)dτ.

(39)

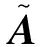
(40)

進一步計算可得LESO的穩態誤差上界

(41)

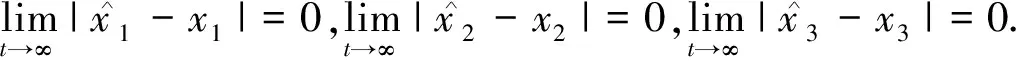
顯然對于ILESO，它的穩態誤差也是有界的，在傳統LESO的基礎上，其形式如下：

(42)

因此可得結論：當線性時不變系統含有擾動，且擾動的導數有上界δ，那么ILESO的跟蹤誤差也有界，且遠小于δ.進一步增大觀測器增益系數，可以降低跟蹤誤差，即達到一種實用穩定.

對于ILESO，因為λ>1,θ>1，在相同條件下，其跟蹤誤差相比于傳統LESO更小.

4 ILESO的時域暫態性能

4.1 調節時間

調節時間是指響應到達并保持在終值±5%或±2% 誤差內所需的最短時間[19]，根據欠阻尼二階系統的時域性能指標的結論，選取誤差帶Δ=0.02，根據式(33)，調節時間可表示為

ts=4.4/a.

(43)

在式(27)中，參數a是調節因子θ和λ的隱函數，分別對θ和λ求導可得

(44)

(45)

綜合式(6)、(21)和(23)可知，a′(θ)>0，a′(λ)<0恒成立，因此參數a與θ正相關，與λ負相關.

綜上所述，增大調節因子θ或者減小λ，都會使調節時間減少，從而加快系統響應速度.

4.2 超調量

根據欠阻尼二階系統的時域性能指標的結論[19]，超調量可以表示為：

(46)

下面對超調量作進一步的討論.

(i) 調節因子λ不變，調節θ.

聯立式(23)和(30)，可得參數a的取值范圍如下：

(47)

將式(44)化成如下形式：

(48)

其中m=β1-2a，且3m+θβ2/m-2β1>0.根據式(47)可知

(49)

在式(26)中，參數b是調節因子θ的隱函數，對θ求導可得

(50)

將式(48)代入式(50)中可得

(51)

綜合式(6)和(49)可知，當滿足式(21)的條件時，重寫為

可以保證b′(θ)>0恒成立.

a/b同樣是調節因子θ的隱函數，對θ求導可得

(52)

將式(48)和(50)代入式(52)中，聯立式(26)可得

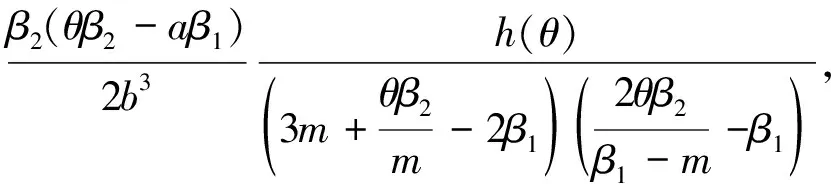
(53)

其中

(θβ2-m(β1-m)).

(54)

綜合式(49)可知，當θ>1時

(55)

h(θ)>0恒成立，所以a/b和調節因子θ正相關.

(ii) 調節因子θ不變，調節λ.

綜合分析式(26)，考慮到式(47)，易知參數a和b負相關，即a/b和調節因子λ負相關.

綜上所述，增大調節因子θ或者減小λ，都會使超調量σ%減少.

4.3 峰值時間

峰值時間是指階躍響應超過終值，到達第一個峰值所需的最短時間[19].可以表示為

(56)

根據前面對參數a和b的分析可知，增大調節因子θ或者增大λ，都可以使峰值時間減小.

圖1 ILESO擾動跟蹤階躍響應曲線Fig.1 Step response curve of ILESO’s noise track

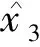
圖1(a)仿真結果說明，增大調節因子θ可以減少調節時間、超調量和峰值時間；圖1(b)說明，增大調節因子λ會增大調節時間和超調量，但峰值時間減小.該結論與上述理論分析吻合.

值得注意的是，如一直增大θ，則會破壞式(30)和(32)的約束條件，且超調量會消失，調節時間會轉而增加，響應會變緩慢，因此調節因子θ不能無限增加.

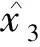
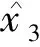
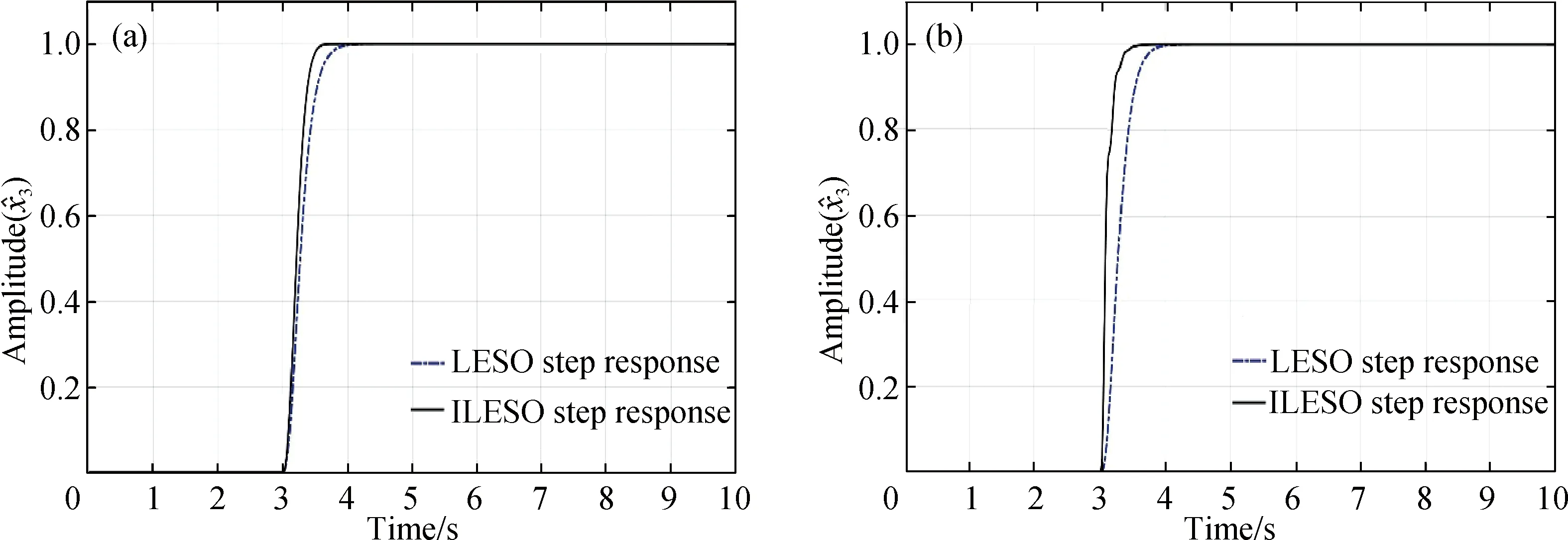
(a)LESO和ILESO帶寬相同; (b)ILESO帶寬大于LESO.圖2 LESO和ILESO擾動跟蹤階躍響應曲線Fig.2 Step response curve of LESO and ILESO’s noise track

從圖2(a)中可以看出，在帶寬近似相同，即觀測器對擾動抑制能力不變的情況下，依靠調節兩個因子可以使得ILESO的峰值時間比LESO更短，響應速度更快.從圖2(b)中可以看出，增大帶寬可以加快系統響應速度，該結論與已有經驗吻合.

5 ILESO的帶寬

將式(33)中的Ψ(s)近似看作ILESO擾動跟蹤的閉環傳遞函數.根據閉環系統的頻域性能指標[19]，設ILESO的觀測帶寬為ωb，可以列出如下方程：

(57)

化簡可得

(58)

(59)

綜合4.1～4.3節中的結論可知，增大調節因子θ或者增大λ，都會使觀測帶寬ωb增加；并且ILESO的觀測帶寬ωb可以由式(23)～(25)和式(59)定量計算得到.

為了驗證上述分析，設定ωc=5 rad/s,ωo=20 rad/s，調節因子λ=80，θ分別取值為10，12，14，15，根據2.2節中式(20)給出的ILESO擾動跟蹤的閉環傳遞函數，繪制bode圖對比曲線如圖3(a)所示，bode圖中橫坐標是擾動頻率，縱坐標分別是信號幅值和相位.

其他條件不變，設定調節因子θ=10，λ分別取值為50，60，70，80，ILESO擾動跟蹤的閉環傳遞函數的bode圖對比曲線如圖3(b)所示.

從圖3(a)可以看出，增大調節因子θ，ILESO的觀測帶寬ωb增加；從圖3(b)可以看出，增大調節因子λ，ILESO的觀測帶寬ωb增加.該結論驗證了上述理論分析的正確性.

6 ADRC整體仿真

6.1 傳統LESO

綜合式(1)、(3)、(7)和(9)，搭建LADRC的Simulink仿真框圖，并編寫相應Matlab程序.將兩個調節因子θ和λ分別置為1，此時ILESO等同于傳統LESO.設定輸入v為單位階躍信號，LESO的帶寬ωo為20 rad/s，控制器帶寬ωc為5 rad/s，并使系統(1)控制輸入系數b0=1.

假設總擾動包含的正弦波頻率為18(rad/s)，矩形波周期為π(s)，斜坡信號斜率為0.5，即

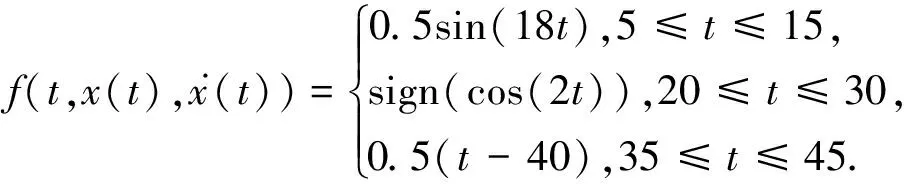
(60)

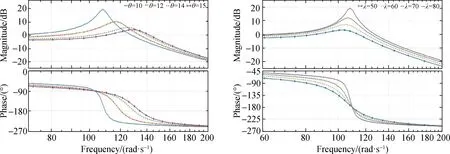
(a)調節因子θ對ILESO帶寬的影響(λ=80); (b)調節因子λ對ILESO帶寬的影響(θ=10).圖3 ILESO擾動跟蹤的bode圖Fig.3 Bode diagram of ILESO’s noise track

仿真結果如圖4所示，圖中橫坐標是仿真時刻，縱坐標是信號幅值，測得此時矩形波的調節時間為ts≈0.45 s.

6.2 改進型LESO(ILESO)

重新設置調節因子θ=1.08,λ=1.785，保持 3.1節中其余仿真參數和仿真條件不變.此時ILESO的帶寬ωb=22.6 rad/s≈ωo，測得調節時間ts<0.35 s，超調量σ%<12%，仿真結果如圖5(a)～(d).

重新設置調節因子θ=15.5,λ=80，保持3.1節中其余仿真參數和仿真條件不變，此時ILESO觀測帶寬ωb≈205 rad/s，仿真結果如圖5(e)～(h).

從圖5(a)～(d)可以看出，在與傳統LESO的帶寬ωo基本保持不變的情況下，正弦波、矩形波、斜坡的暫態響應速度已經明顯加快.從圖5(e)～(h)可以看出，當放開對帶寬的限制時，靈活改變兩個調節因子θ和λ的值，矩形波的調節時間和超調量幾乎可以忽略不計，正弦信號跟蹤誤差也大幅減小.

對比圖4和圖5可以看出,ILESO只需通過兩個調節因子的搭配就可以優化觀測器的調節時間和超調量，靈活調節暫態響應的速度和跟蹤誤差.

7 結 論

針對二階系統ADRC的LESO暫態跟蹤性能的不足和帶寬之間的矛盾，提出了一種ILESO.在傳統“帶寬法”配置極點的基礎上，在觀測器方程中增加兩個調節因子，從而可以根據外部噪聲的頻率和內部擾動的特征，靈活配置極點位置，增進了觀測器的暫態性能.擾動觀測帶寬的大小可以根據實際情況靈活調節，增強了對噪聲的抑制能力.通過理論分析，得到兩個調節因子與系統暫態性能、帶寬之間的定性關系.通過實驗仿真對比，證明了該方法的優越性，為實際的工程控制應用提供了一種新方法.本文中基于“帶寬法”提供了時域分析的一種方法，另一種思路是直接通過“主導極點”分析給出暫態性能和觀測器主導極點參數之間的關系，是值得將來進一步考慮的問題.