動態凍結磁導率法用于波動負載電機磁場分析

邱小華，徐 飛，尹華杰

(1.廣東美芝制冷設備有限公司，佛山 528399；2.華南理工大學電力學院，廣州 510640)

0 引 言

在電機仿真中，動態凍結磁導率磁場仿真是一種比較普遍的需求。例如，文獻[1]詳細介紹了凍結磁導率功能在電機性能分析上的應用，其中如轉矩紋波的分析、功角特性中基本電磁功率和附加電磁功率的分析等，就需要用到動態凍結磁導率功能。文獻[2-3]介紹了永磁電機轉矩分離的方法，也需要進行動態磁導率凍結。在研究永磁電機的電磁振動和噪聲時[5]，利用動態凍結磁導率方法來分離動態磁場中的永磁場和電樞反應磁場，對于探明電磁噪聲的根源也是十分重要的手段。

然而，以ANSYS EM為代表的一些電磁仿真軟件，僅在靜磁場仿真和渦流場仿真時能進行凍結磁導率操作，而在動態磁場仿真時，除了在電感計算時程序內部會自動凍結磁導率外[4]，并沒有開放凍結磁導率的功能給用戶進行不同激勵磁場的分離。從已發表的一些文獻來看，用戶動態凍結磁導率都是利用現有電磁仿真軟件的靜態凍結磁導率功能來實現的[2-6]，但具體如何進行，相關的程序代碼等則未見有文獻涉及；對于波動負載、轉速不恒定的情況，更未見有動態凍結磁導率的報道。

本文設計了在ANSYS EM下進行動態凍結磁導率的方法和步驟，其思路是將電機定、轉子分成可以沿著氣隙中的一條圓弧分界線相對轉動的兩個獨立的建模區域，并定義二者的相對轉角為掃描參數，應用參數掃描功能(或從外部程序)控制轉角參數按固定步長變化(恒速仿真時)或按可變步長變化(帶波動負載、轉速不恒定時)，使用靜磁場凍結磁導率功能，計算每個角度的總磁場、永磁場及電樞磁場，達到動態凍結磁導率的效果；并將該方法用于一臺壓縮機用9槽6極永磁同步電機的磁場及徑向力的分析，取得了較滿意的效果。

1 ANSYS EM動態磁場凍結磁導率法

1.1 凍結磁導率的原理

如圖1所示，電機磁路都存在一定程度的飽和，因此，定、轉子共同勵磁場強Hcb(工作點a)、永磁體單獨勵磁場強Hpm(工作點b)、電樞電流單獨勵磁場強Hi(工作點c)三者產生的磁密Bcb、Bpm、Bi不滿足線性疊加原理，即Hpm+Hi=Hcb，但Bpm+Bi>Bcb。

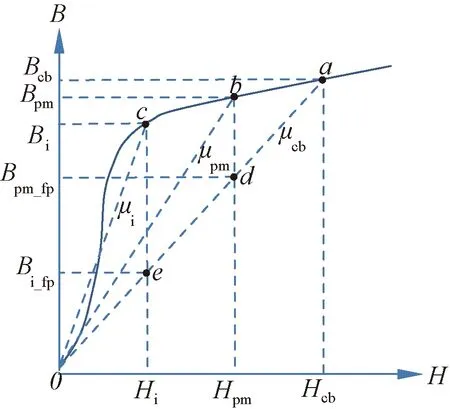
圖1 凍結磁導率方法示意圖

為了獲得定、轉子勵磁分量正確的磁密貢獻，在有限元計算時，先計算共同勵磁Hcb的磁密Bcb(工作點a)，并保存各剖分單元當前的磁導率，這是一次非線性磁場求解；再利用保存的各單元磁導率，計算Hpm或Hi單獨存在時的磁密Bpm_fp或Bi_fp(工作點d或e)，這是兩次線性磁場求解。由于工作點a、d、e位于過原點的直線上，因此滿足線性疊加原理，即三個勵磁產生的磁密滿足Bpm_fp+Bi_fp=Bcb。這就是凍結磁導法。

動態凍結磁導率仿真就是在仿真電機的起動過程或其他動態過程時，在每一個仿真時間點或每一步中，除了要進行總勵磁的磁場計算外，還要保存每個單元的磁導率，對定子或轉子單獨勵磁的磁場進行計算，從而達到在動態過程的每一步中分離永磁磁場、電樞反應磁場的效果。

1.2 ANSYS EM靜磁場凍結磁導率的設置

文獻[6]介紹了用戶凍結磁導率的步驟。為方便讀者參考，下面扼要說明：

(1)在建好的靜磁場仿真模型設計中，在Analysis命令單下新建一個Setup并打開，找到Solver選單，勾選“Use pre-computered permeability data(使用預先算得的磁導率)”；若是提取永磁場，則勾選“Including magnets”，并在勵磁設置中將繞組電流置0；

(2)再點擊“Setup Link…”，在General選單中進行磁導率來源的設置，包括：源工程、源設計、源setup、是否重新仿真源設計、重新仿真的話是否保存結果等；

(3)在Variable Mapping(變量映射)選單中，設置源設計、目標設計的變量間的映射關系為“按變量名映射”；

(4)然后運行(1)中新建的Setup，即可求解永磁勵磁或電樞勵磁的貢獻。

1.3 動態凍結磁導率方法

ANSYS EM在動態磁場仿真時，利用Band類型的扇形或圓形區域覆蓋轉子區域，自動處理轉子的旋轉，十分方便。但可惜的是，動態仿真不支持用戶凍結磁導率，而靜磁場仿真則不支持Band區域類型。為突破這一限制，如圖2所示，將電機模型分為定子和轉子兩個獨立區域，設置轉角變量θ，以固定的(或變化的)步長改變θ，實現轉子相對定子旋轉的目的，并在每步中應用靜態凍結磁導率功能計算電機的總磁場、永磁場、電樞磁場，從而達到動態凍結磁導率的效果。具體說明如下：

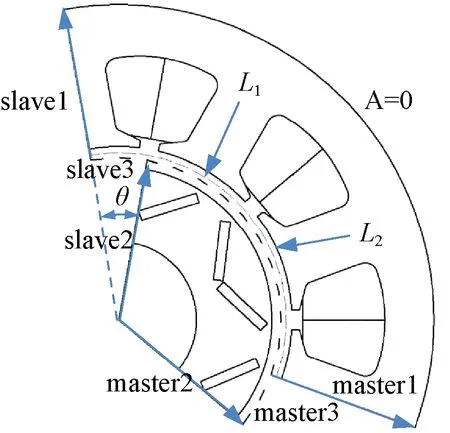
圖2 ANSYS EM動態凍結磁導率時的邊界條件設置

(1)定、轉子由圓弧L1分隔，定、轉子可以沿著圓弧L1相對滑移；靠近定子側的圓弧L2用于提取氣隙磁場；

(2)幾何建模時，選中定子(或轉子)的全部子域，使之旋轉θ角，則以后改變θ時，該部分區域的旋轉量就會相應地自動改變；

(3)按實際問題設置周期(或半周期)邊界條件(使用360°的全模型可以繞過這個設置難點)；

(4)以轉角θ為參數，設置定子A、B、C三相電流：若電流與θ不是簡單的函數關系(而是預先算得的時間函數曲線)，則添加Dataset類型的變量來保存電流曲線，并使用分片線性插值函數pwl，用Dataset變量插值來確定特定時刻的電流；

(5)如果旋轉的是轉子，則永磁勵磁須采用體坐標系(Body CS)定義，且應勾選“Always Move CS to End”，否則勵磁方向不會隨θ旋轉；

(6)轉角θ的掃描設置：在“Optimetrics(優化)”中設置θ的掃描(如果不是勻速旋轉，則可定義時間變量t作為掃描參數，并添加Dataset類型變量來保存θ曲線，用pwl函數來確定θ)；

(7)復制、粘貼建好的設計共3份，分別命名為“全磁場設計”、“電樞磁場設計”、“永磁場設計”；

(8)按上節的方法對“電樞磁場設計”、“永磁場設計”的凍結磁導率選項進行設置；

(9)θ或t的掃描：先完成“全磁場設計”的掃描，再進行“電樞磁場設計”、“永磁場設計”的掃描；

(10)全部掃描完成后，繪制每個設計在圓弧L2上的徑向磁場、切向磁場、徑向力等曲線，并輸出為*.CSV格式的數據文件，用于MATLAB或Octave做二維快速傅里葉分析(FFT2)。

1.4 用Octave控制動態凍結磁導率

上節介紹的動態凍結磁導率方法用于電機勻速旋轉、電流按正弦規律變化的情況比較方便，用于非勻速的情況則要用到Dataset類型的變量來導入表格，并用pwl函數插值，設置比較復雜。以下介紹利用Octave或MATLAB軟件，從外部改變轉角、電流，控制ANSYS EM進行動態凍結磁導率仿真的方法。

首先，將MATLAB-Simulink、Psim或Plecs等軟件動態仿真所得的(或實驗所得的)電機轉角及三相電流等按固定的時間步長保存到文本文件；再將它們讀入到Octave的數組中；然后針對每個時間點，用Octave腳本修改ANSYS EM設計的轉角變量和電流變量，并依次仿真前述的3個設計、保存它們的氣隙磁密或徑向力；待全部時間點仿真完成后，再進行FFT2處理。其中關鍵的幾句腳本如下：

(1)建立兩個程序間的Com通信接口：iMaxwell=actxserver('Ansoft.ElectronicsDesktop')(若用Octave而非MATLAB，則需先在命令窗口運行pgk load windows,否則actxserver無效)；

(2)獲取當前ANSYS EM的桌面句柄：Desktop=iMaxwell.GetAppDesktop();

(3)激活設計所在的工程：Project=Desktop.SetActiveProject('工程名');

(4)激活要仿真的設計：Design=Project.SetActiveDesign('設計名');

(5)修改設計的參數：

Design.ChangeProperty( {'NAME:AllTabs',…

縱觀三季度的冰箱線上市場，三門、多門、對開門冰箱呈現出不同幅度的增長，以多門勢頭最盛，漲幅高達61.9%；而線下除多門冰箱有7.5%的增長外，其他品類均出現不同程度的下跌。總體來看，多門冰箱表現搶眼，已成為消費者的主流選擇，且上升趨勢十分明顯；對開門冰箱上升勢頭有所放緩，但依然是不少消費者的最終選擇；三門冰箱以高性價比也獲得了越來越多的線上客戶青睞，但在對消費體驗要求更高的線下市場，已經少有昔日風光；兩門冰箱則逐漸式微，尤其在線下市場，消費者的目光更容易被中高端產品吸引。

{'NAME:LocalVariableTab',…

{'NAME:PropServers','LocalVariables'},…

{'NAME:ChangedProps',…

{'變量名','Value:=','變量值'}}}});

(6)運行設計的setup1：Design.Analyze('Setup1')。

以上第5條語句較為復雜，有疑問的讀者可以在ANSYS EM的“Tools”菜單中執行“記錄腳本到文件”，并試著改變某個參數，然后查看記錄下的腳本文件做進一步的了解。

2 永磁同步電機波動負載的磁場及電磁力分析

應用上述動態凍結磁導率磁場仿真方法，對一臺結構如圖2所示的9槽6極內置轉子永磁同步電機帶壓縮機波動負載在3 600 r/min平均轉速下的磁場及徑向力進行了仿真分析。

圖3為動態凍結磁導率仿真所用的轉角、三相電流曲線，這可以由電路仿真軟件提供，也可由實驗提供。基于內置轉子永磁同步電機的集中參數以及具體的壓縮機負載，在MATLAB/Simulink下建立矢量控制動態仿真模型，并選取仿真結果達到穩定后轉角和電流波形的最后一個完整機械周期。

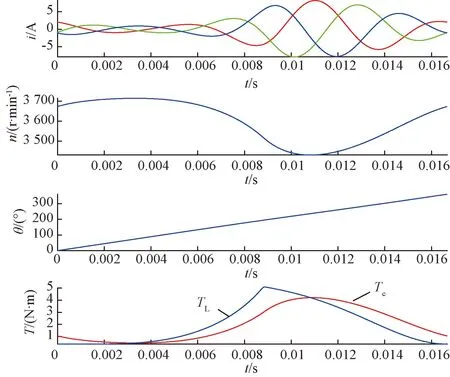
圖3 一臺內置轉子永磁同步帶壓縮機負載、3 600 r/min時，轉子旋轉一圈的三相電流、轉速、轉子轉角、電磁轉矩及負載轉矩波形

動態凍結磁導率的磁密時空波形如圖4所示。可見，永磁場占主導地位，電樞磁場占比較小；總磁密及永磁磁密的幅值隨時間變化不明顯，但電樞磁密的幅值隨時間變化很大，這與圖3的三相電流波形的變化是相對應的。

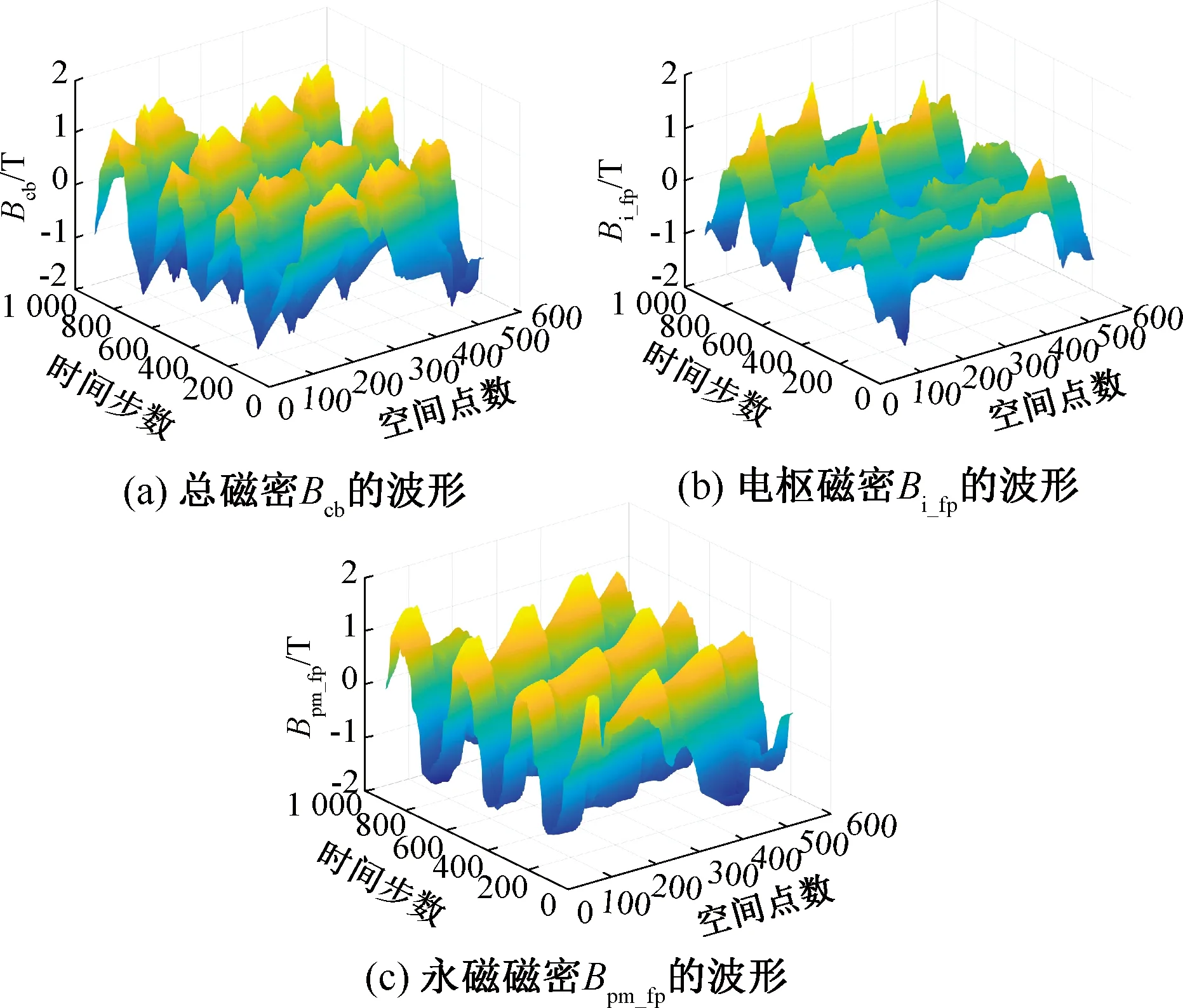
圖4 內置轉子永磁同步電機帶動態負荷時的總磁密、分量磁密波形

各磁密波形的二維傅里葉分解(FFT2)時空諧波如圖5所示。為方便描述，在下面的分析中，將一個極對數為np、頻率為mfm的時空諧波表示成(np,mfm)的形式，其中：p為電機的極對數，本文的p=3；n為極對數的倍數，可取任何整數；fm為轉子的旋轉頻率，且有1fe=pfm，fe為基波電頻率；m為fm的倍數，可取任何非負整數。

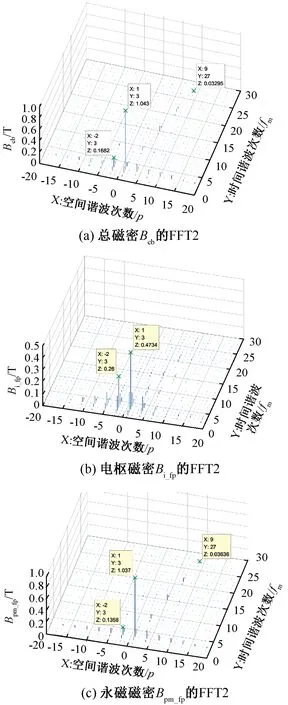
圖5 內置轉子永磁同步電機總磁密、各分量磁密的時空諧波桿狀圖

在永磁磁密諧波圖5(c)中，幅值較大的磁密諧波主要位于兩條直線上：一條為(np,3fm)，各諧波都具有基波電頻率，是永磁基波磁動勢(1p,3fm)與定子槽磁導諧波(3kp,0fm)作用的結果；另一條為(np,n3fm)，各諧波都具有同步旋轉速度，是永磁磁動勢諧波(np,n3fm)與氣隙平均磁導(0p,0fm)作用的結果。此外，在以上兩類主要磁密諧波的旁邊，還存在頻率變化±1fm且幅值較大的諧波，這是因轉速以1fm的頻率波動而在主要磁密諧波旁邊調制出來的諧波。永磁磁密基波(1p,3fm)的幅值最大，其次是(-2p,3fm)。

在電樞磁密諧波的圖5(b)中，主要諧波都在(np,3fm)的直線上，各諧波都具有基波電頻率。此外，在以上(np,3fm)磁密諧波的附近，還存在頻率變化±1fm、±2fm且幅值較大的諧波，這是因為負載的1fm波動導致轉速及有功電流也以1fm的頻率波動，因而調制出了這些諧波。在所有電樞磁密諧波中，基波(1p,3fm)的幅值最大，反轉的二次諧波(-2p,3fm)次之。

由圖5(a)的總磁密桿狀圖可見，總磁密主要有三個比較大的分量，幅值最大的為基波(1p,3fm)，其次是反轉的二次諧波(-2p,3fm)，再次是正轉的4次諧波(4p,3fm)。此外，也存在一定程度的2fm和4fm頻率的調制諧波。

利用圖5的磁密時空諧波結果來計算徑向電磁力，可得圖6的徑向力時空諧波圖(剔除靜態的0頻分量)。可見，除了電機中常規的(2p,6fm)徑向力波外，還出現了幅值較大、頻率為5fm、7fm、1fm的徑向力波，這是磁密調制的結果，即徑向力波中也存在因負載和轉速的波動而引起的調制波。

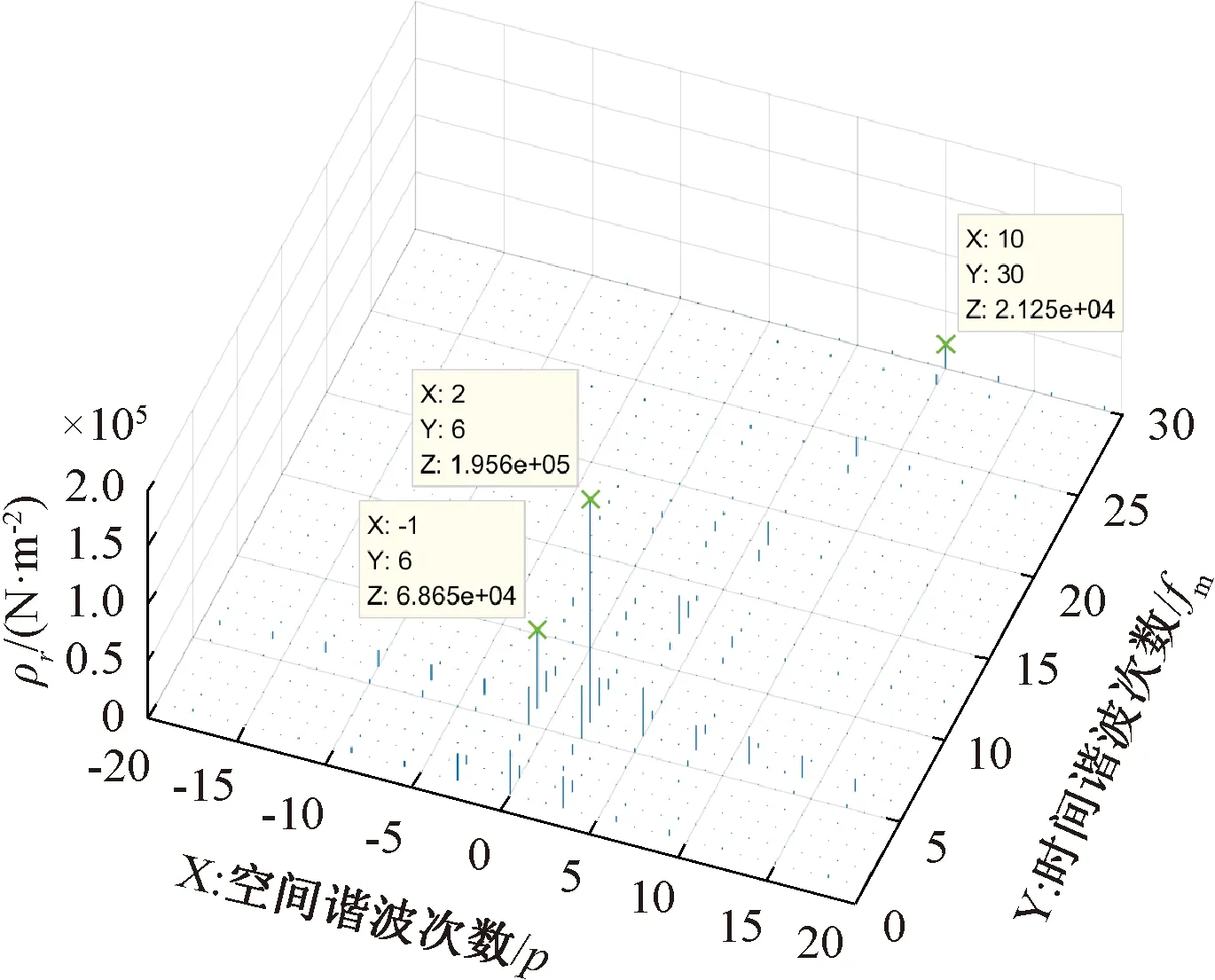
圖6 內置轉子永磁同步電機帶動態負荷時的徑向力諧波桿狀圖

3 結 語

本文針對帶波動負載的電機需要對各勵磁分量磁密進行分離的要求，介紹了一種基于ANSYS EM靜態凍結磁導率功能來實現動態凍結磁導率磁場仿真的方法，尤其針對轉速波動的情況，給出了應用Octave或MATLAB腳本控制ANSYS EM進行動態磁場凍結磁導率仿真的方法、步驟，并將該方法用于一臺9槽6極帶壓縮機負載的內置轉子永磁同步電機的氣隙磁場分離、諧波分析、徑向電磁力分析，發現相對于恒定負載勻速運行的情況，波動負載在原有的主要磁密諧波的旁邊，產生了頻率增加或減小1倍甚至2倍機械頻率的調制諧波，徑向力波中也相應地存在調制諧波。