基于改進強跟蹤濾波器的PMSM矢量控制

孟得龍，李寧洲，衛曉娟

(蘭州交通大學 機電工程學院，蘭州 730070)

0 引 言

近些年來，無速度傳感器控制因為運行成本低，運行性能良好，成為電機控制領域的研究熱點。文獻[1]模型參考自適應算法估計永磁同步電機轉子位置角及轉速，實現無速度傳感器控制。文獻[2]采用模糊超螺旋算法二階滑模觀測器，提高了轉子位置估計精度，增強了控制系統的魯棒性。擴展卡爾曼濾波算法以及改進的擴展卡爾曼濾波算法因為能夠對系統狀態實行在線估計，進而實現對系統的實時控制，也被廣泛應用于電機控制領域[3-4]。文獻[5]利用擴展卡爾曼濾波算法估計電機電流，實現了無電流傳感器控制,對于電機轉速及轉子位置未進行研究。文獻[6-8]分別采用中心差分擴展卡爾曼濾波算法、抗差擴展卡爾曼濾波算法以及改進的模糊卡爾曼濾波算法對感應電機進行轉速估計，取得了良好的控制效果，提高了轉速估計精度，但增加了計算過程的復雜程度。文獻[9]采用低階串行雙擴展卡爾曼濾波算法，實現了永磁直線同步電機無速度傳感器控制系統的設計，同樣計算過程復雜。文獻[10]采用平方根卡爾曼濾波算法對永磁同步電機實行無速度傳感器控制，仿真效果良好。文獻[11-13]采用擴展卡爾曼濾波算法估計電機轉速及轉子位置角，算法簡單，但估計精度不高，濾波效果較差。

本文在擴展卡爾曼濾波(以下簡稱EKF)的基礎上，采用帶多重漸消因子的強跟蹤擴展卡爾曼濾波算法來估計轉速及轉子位置，不僅提高濾波的穩定性和收斂性，而且算法相對簡單，易于實現。

1 傳統擴展卡爾曼濾波器算法

表貼式三相永磁同步電動機(以下簡稱PMSM)在靜止坐標系下的電壓方程[14]：

(1)

將式(1)變換為電流方程，可得：

(2)

考慮到式(3)所示關系：

(3)

由式(1)、式(2)、式(3)得到如下的狀態方程：

(4)

y=Cx

(5)

式中：

(6)

(7)

(8)

將式(4)和式(5)離散化，可得：

x(k+1)=f[x(k)]+B(k)u(k)+V(k)

(9)

y(k)=C(k)x(k)+W(k)

(10)

式中：V(k)為系統噪聲;W(k)為測量噪聲。

傳統擴展卡爾曼濾波器的狀態估計可分為以下幾個步驟：

(1)一步預測：

(11)

式中：Ts為采樣時間;“～”表示預測值;“^”表示估計值。

(2)計算此預測對應的輸出：

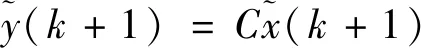
(12)

(3)計算預測協方差陣：

(13)

式中：

(14)

結果為：

(15)

(4)計算EKF的增益矩陣:

(16)

(5)計算優化狀態估計值：

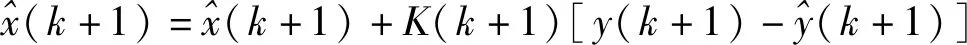
(17)

(6)計算估計誤差協方差矩陣：

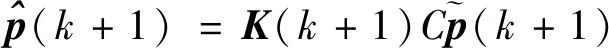
(18)

2 帶多重次優漸消因子的擴展卡爾曼濾波算法[15]

由于傳統卡爾曼濾波算法在對狀態變量估計的過程中精度不高，有學者提出帶次優漸消因子的擴展卡爾曼濾波算法。同時，為克服漸消因子易引起過調節這一問題，在算法中引入弱化因子。

根據殘差序列的正交性原理，如式(19)所示。同時，定義式(20)：

(19)

(20)

式中：β≥1為弱化因子;Vk為殘差協方差矩陣;Hk為觀測矩陣;Q,Rk為噪聲協方差矩陣。定義如下：

(21)

式中：εk為殘差序列，εk=zk-zk/k-1；0<ρ≤1為遺忘因子，通常取ρ=0.95。

對式(20)兩端求矩陣的跡，可以得到漸消因子λk的次優解：

(22)

式中：

(23)

式中：tr[ ]為矩陣的跡。

將式(22)代入到式(13)中，可以得到帶單一次優漸消因子的狀態誤差協方差矩陣：

pk/k-1=λkFkpkFk+Q

(24)

由于篇幅限制，帶漸消因子的卡爾曼濾波穩定性推導不再進行贅述。

系統模型的不確定性在不同狀態時的影響是不同的，采用單一漸消因子時，狀態跟蹤性能不理想。因此，為進一步提高濾波器的強跟蹤性能，本文采用帶多重次優漸消因子的擴展卡爾曼濾波器(SMFEKF)。由式(24)及系統先驗知識，可以大致確定：

(25)

令：

(26)

式中：αi≥1均為預先選定的常數，由先驗信息確定；ck為待定因子。則可以確定多重次優漸消因子的一般算法如下：

(27)

同時，將式(25)代入式(24)可得：

(28)

總結上述推導過程，多重次優漸消因子λk求解算法如下：

(29)

由擴展卡爾曼濾波算法結合，式(25)～式(29)便可以得到SMFEKF算法。至此，SMFEKF算法所需參數以及公式全部給出。

圖1為基于SMFEKF的PMSM磁場定向控制仿真框圖。圖2為SMFEKF模塊。

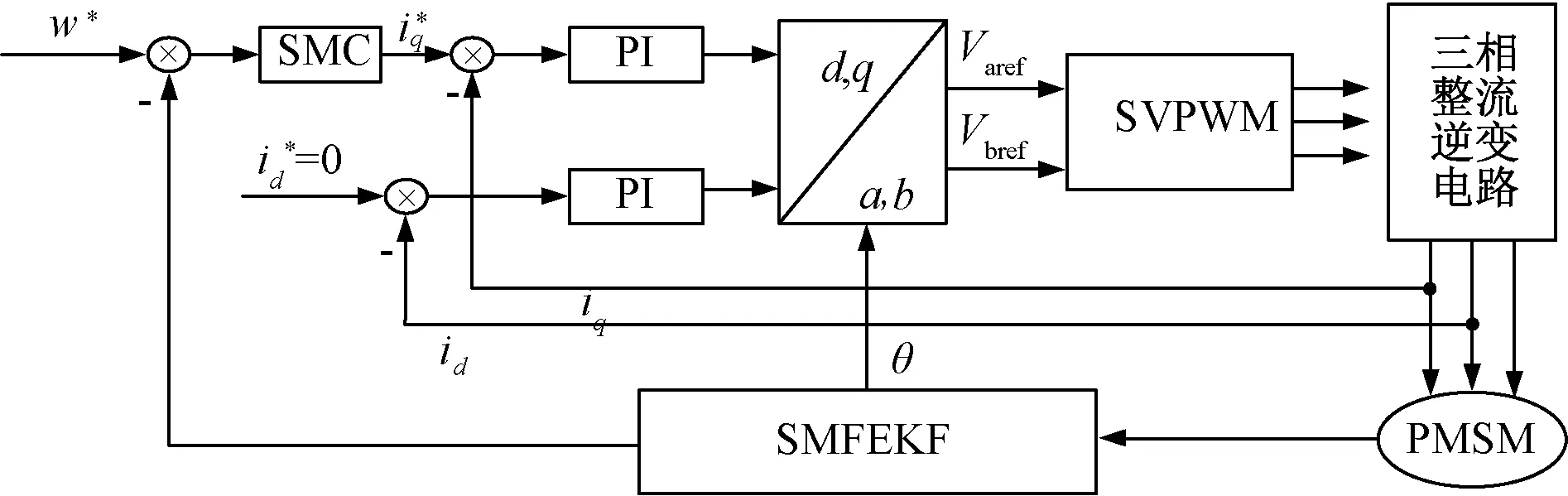
圖1 基于SMFEKF的PMSM磁場定向控制仿真框圖

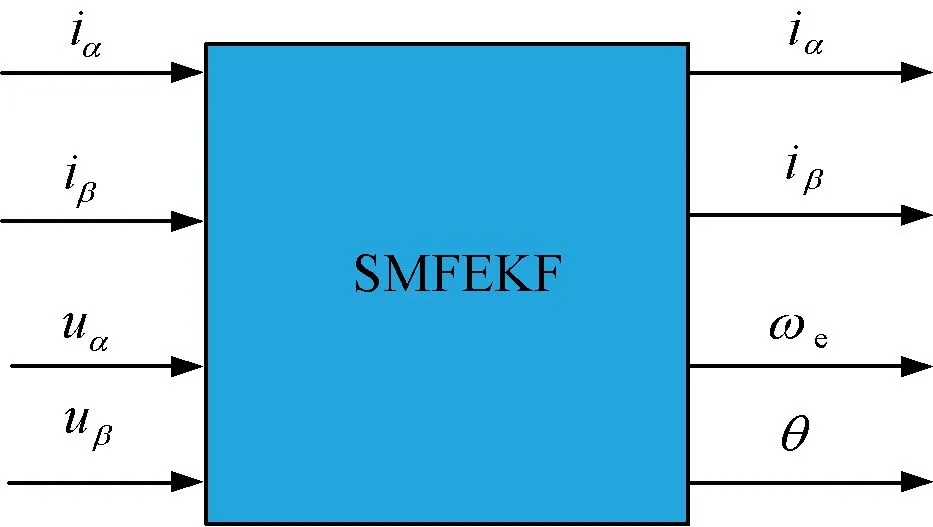
圖2 SMFEKF算法框圖

3 仿真結果

仿真用到的PMSM主要參數：Rs=2.875 Ω；Ld=8.5 mH；Lq=8.5 mH；φf=0.175 Wb；J=0.003 kg·m2；p=4；系統仿真時間t=0.4 s；給定速度為1 000 r/min；在起動0.1 s后給定負載轉矩15 N·m。仿真結果如圖3～圖6所示。

由圖3可知,SMFEKF矢量控制相比傳統擴展卡爾曼算法(EKF)，在轉矩輸出方面，脈動成分降低，穩態性能良好。在0.1 s突加負載時，轉矩的響應速度較快，上升比較平穩。

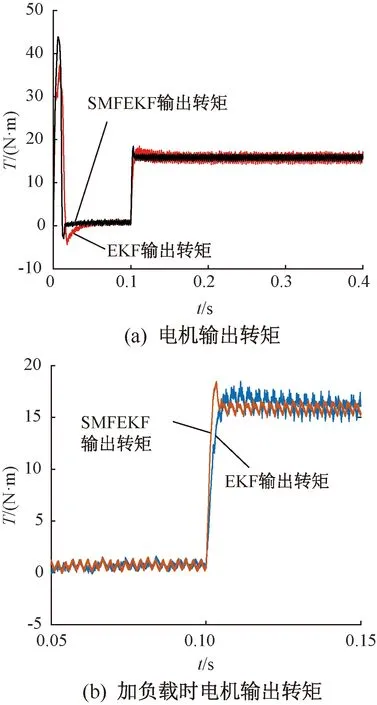
圖3 電機轉矩

由圖4可知,電機輸出轉速響應較快，轉速估計未出現超調現象，動態響應效果明顯改善。在0.1 s施加負載轉矩時，轉速出現小幅下降，但很快達到給定轉速，并穩定運行。從圖4(b)可知，基于SMFEKF的轉速差在電機起動階段，超調量大幅降低，并最終穩定在零值附近。

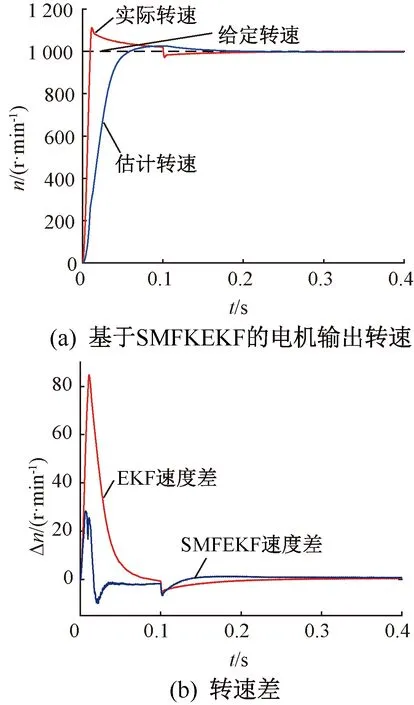
圖4 電機轉速及轉速差

由圖5可知，估計的轉子位置角能夠準確追蹤電機實際轉子位置角，在0.1～0.4 s電機穩定運行階段，基于SMFEKF估計誤差明顯小于EKF估計誤差，在一定程度上提高了無位置傳感器控制的運行性能。圖6為電機α軸定子電流。

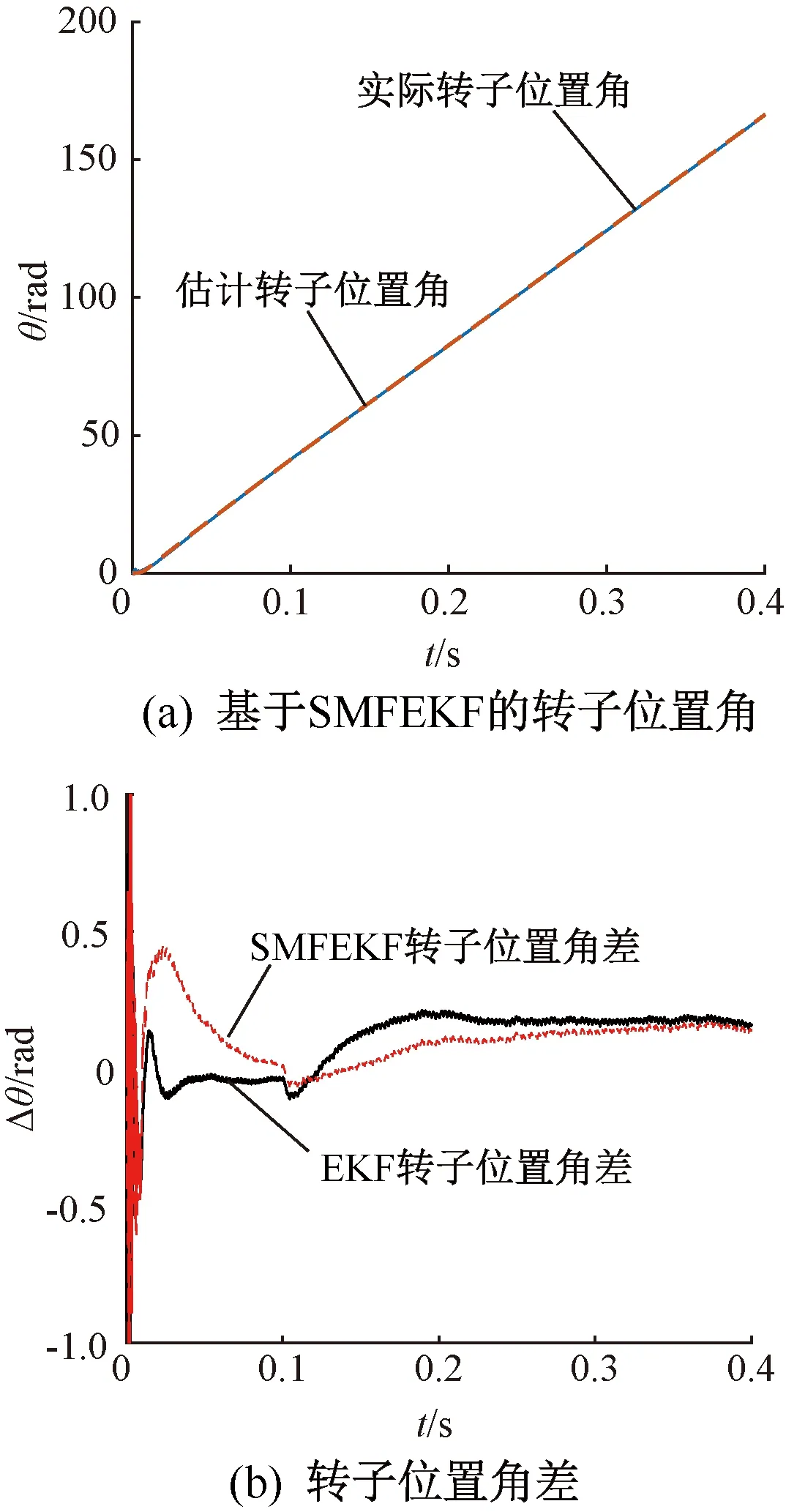
圖5 電機輸出轉子位置角

從圖6中可以看出，估計電流能夠較好地跟蹤實際電流，且電流波形具有較高的正弦度，未出現明顯畸變。

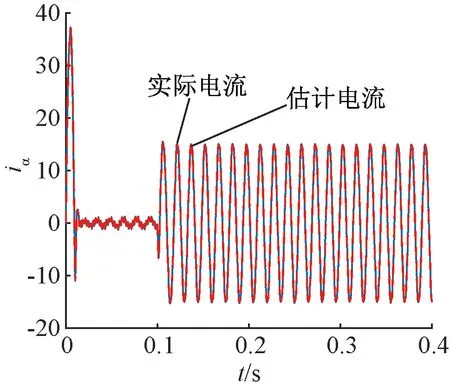
圖6 α軸定子電流

4 結 語

本文在 PMSM兩相靜止坐標系數學模型基礎上，設計基于SMFEKF的無速度傳感器矢量控制系統。仿真結果表明:該系統不僅能夠準確估計出轉子空間位置和轉速，同時減少了電機輸出轉矩的脈動成分，具有良好的運行性能。由于PMSM是一個多變量、強非線性的系統，通過辨識系統參數來提高轉速估計精度和增強系統魯棒性還需在后續工作中作進一步研究。