螺旋彈簧橫向靜剛度計算及動剛度頻變分析

張名揚，張開林，姚遠

(西南交通大學 牽引動力國家重點實驗室，四川 成都 610031)

0 引言

等截面圓柱形螺旋壓縮彈簧因結構簡單可靠、變形范圍寬泛等優點廣泛應用于儀表、電器、交通運輸等行業[1-3]。在軌道交通領域，螺旋彈簧被大量應用在機車車輛的懸掛裝置上，起緩和因輪對行徑線路不平順、軌縫、道岔、鋼軌磨耗和不均勻下沉以及車輪不圓、軸頸偏心等原因引起的振動和沖擊[4]。螺旋彈簧的動態傳遞特性顯著影響著列車運行的安全性、平穩性和舒適性，準確分析其剛度特性是保證動力學計算精度的前提。

輪軌沖擊振動對列車運行速度十分敏感。列車在高速運營時，輪軌間動作用力顯著增強，激勵頻率范圍變寬[5]。激勵產生的中高頻振動傳遞到轉向架及車體，造成零部件的振動特性與低速時大不相同[6]。當列車側向通過道岔時，劇烈的輪軌橫向沖擊將導致十分復雜的輪岔動態相互作用，引起車輛較強的橫向振動，導致較大的脫軌系數，對行車安全產生不利影響。彈簧的橫向剛度關系到列車曲線通過性和橫向運動性能，而振動頻率又會影響彈簧動態傳遞特性[7]。現有文獻大多僅對彈簧垂向剛度進行分析，而橫向動剛度的研究近似空白，故探究不同激勵頻率下螺旋彈簧橫向剛度特性是具有理論價值和工程意義的。

本文對螺旋彈簧的橫向靜剛度及動剛度進行有限元分析。依據計算結果，對Krettek剛度公式進行修正，提高公式的計算精度。改變加載條件和彈簧參數，施加橫向正弦位移激勵進行頻變分析，探究影響彈簧動態傳遞特性的因素。

1 螺旋彈簧橫向靜剛度

1.1 Krettek剛度公式

傳統的螺旋彈簧橫向靜剛度計算一般是將彈簧簡化成等截面彈性直桿[8]。定義彈簧等效彎曲剛度B、等效剪切剛度S、垂向靜剛度kv分別為：

(1)

(2)

(3)

式中：d為簧絲直徑；D為彈簧中徑；n為彈簧有效圈圈數；E為彈性模量；μ為泊松比；H為彈簧工作高度，H=H0-fv-d，fv為彈簧垂向壓縮量，H0為彈簧自由高度。

假定彈簧受橫向載荷變形過程中上、下端面始終保持水平，如圖1所示。由于結構具有對稱性，零彎矩點為彈簧中點，取二分之一為研究對象[9]。建立彈簧變形的微分方程，帶入邊界條件，得到彈簧橫向靜剛度kl的理論值為

(4)

其中

(5)

式中Pv為垂向載荷，Pv=kv×fv。

KRETTEK O等[10]引入修正因子α來考慮彈簧fv和H0對橫向靜剛度的影響。Krettek剛度公式為

klk=αkl=(afv/H0+b)×kl

(6)

式中a、b為修正系數。

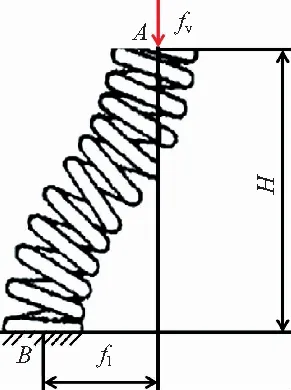
圖1 橫向變形示意圖

1.2 有限元分析

為探究影響彈簧橫向靜剛度的因素，構建兩端磨平的螺旋彈簧有限元計算模型。支撐區域由于形狀相對復雜，采用SOLID95號單元；中間有效區域采用SOLID45號單元。為正確模擬實際工作狀況，將彈簧上、下端面所有節點分別剛性耦合至各自的中心點A點及B點。在B點施加固定端約束，在A點施加垂向及橫向位移載荷。通過靜力分析，在ANSYS軟件的POST26后處理模塊中提取橫向支反力，除以橫向位移量fl，即可得到橫向靜剛度kl的有限元分析結果。

肖緋雄[11]發現橫向載荷的加載方向會對螺旋彈簧垂向靜剛度kv產生影響。為探究加載方向對kl是否有影響，在受載端以A點為坐標原點，建立如圖2所示的坐標系。y軸與受載端切口平面S1的法向相平行，且向外為正。通過改變有效圈和支撐圈的圈數，調整受載端切口平面S1和約束端切口平面S2的相對位置，將兩切口平面所夾角度θ分為4個區間。通過有限元計算，定性分析不同加載方向下kl隨fl和fv的變化趨勢，如表1所示。

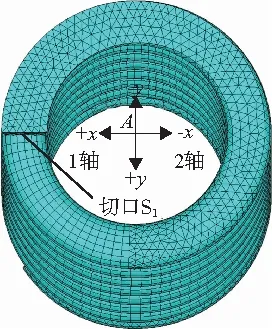
圖2 平面直角坐標系

表1 切口平面不同位置橫向靜剛度變化趨勢

當載荷沿+x向加載，夾角θ在0°～270°范圍內時，kl隨著fl的增加而增加；當θ在270°～360°范圍內時，kl隨fl的增加而減小。沿-x向加載有相反的規律。

當載荷沿+y向加載，夾角θ在0°～180°和270°～360°范圍內時，kl隨著fl的增加而增加；當θ在180°～270°范圍內時，kl隨fl的增加而減小。沿-y向加載有相反的規律。

同時，kl隨著fv的變化趨勢與隨著fl的變化趨勢相反。

以彈簧兩切口平面夾角θ在270°～360°內的模型為例，定量分析橫向載荷加載方向對kl的影響，如圖3所示。依次改變fl和垂向壓縮量fv，繪制kl的變化曲線，如圖4、圖5所示。對于無垂向壓縮的狀態，無論橫向載荷加載方向如何，kl均不隨fl發生改變，沿x軸、y軸加載時的剛度值分別為386.65N/mm和377.62N/mm；對于存在垂向壓縮的狀態，kl隨fl的增加呈負指數次的增加/減小，且最終都趨于無垂向壓縮時的剛度值。當fv遠大于fl時，彈簧垂向變形占主導地位，故kl隨fv的增加呈線性增加/減小，且隨著fl的增加，kl變化速度減緩。

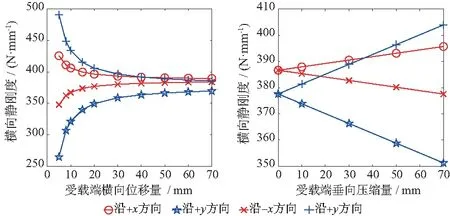
圖3 不同加載方向橫向靜剛度變化曲線

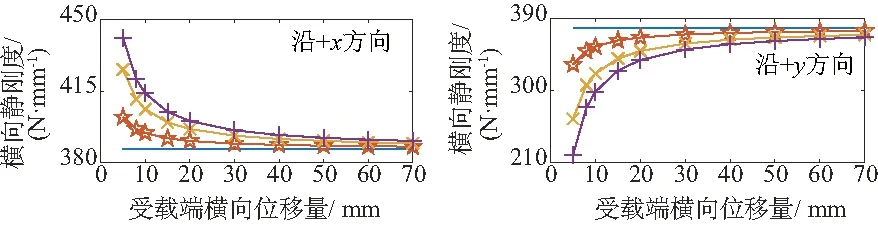
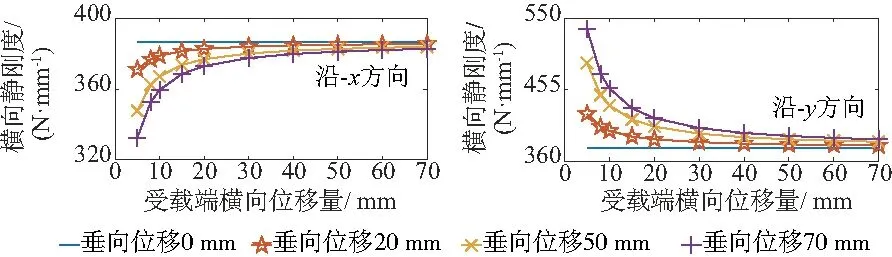
圖4 橫向靜剛度隨橫向位移量變化曲線

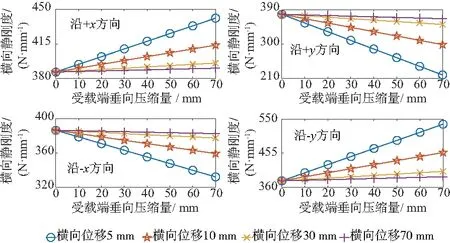
圖5 橫向靜剛度隨垂向壓縮量變化曲線

由上述分析可知，螺旋彈簧受載端的fl和fv都會對彈簧kl產生影響，而Krettek剛度公式僅考慮了fv的影響，故其存在一定偏差。

1.3 橫向靜剛度修正公式

在Krettek剛度公式的基礎上，綜合考慮fv和fl對kl的影響，對參數α進一步優化，建立三參數模型：

(7)

式中a1-a3為修正系數。

為驗證修正公式(7)的普遍適用性，建立不同參數的螺旋彈簧模型。通過對有限元計算結果的擬合，求得各自的橫向靜剛度修正系數，如表2所示。對比發現，對于沿同一軸正、反兩個方向加載的情況，修正系數中只有系數a1存在著正負的差別。螺旋彈簧在鐵路車輛中均對稱布置于構架兩側，為消除橫向位移量對橫向總剛度的影響，右側彈簧可由左側彈簧旋轉180°后安裝。

將不同fv和fl帶入修正后的橫向靜剛度公式(7)，與有限元法相比較的計算誤差見表3。顯然，公式(7)的計算精度和穩定性均優于現有方法。

表2 彈簧幾何參數及修正系數

表3 橫向剛度修正公式計算誤差絕對值 單位：N·mm-1

2 螺旋彈簧橫向動剛度頻變特性

2.1 橫向動剛度變化趨勢

中高頻激勵下，螺旋彈簧自身振動加劇，彈簧各點的運動情況變得非常復雜[12]。特別是當激勵頻率較高時，剛度變化較大，振動傳遞特性與低頻激勵下存在較大差異[13]。為研究彈簧在中高頻激勵下的動態響應，需進行頻變分析。引入動剛度kd來描述彈簧動態傳遞特性。由于螺旋彈簧在中高頻激勵下振動波動傳遞效應的存在，固定端和受載端由彈簧變形而產生的反力不同，將動剛度kd進一步分為點剛度kdP和傳遞剛度kdT[14]：

(8)

式中FWP、FWT分別為彈簧受到幅值為um的正弦位移激勵后，受載端和固定端的反作用力幅值。

在B點施加全約束，在A點施加垂向預壓縮量fv及橫向正弦位移激勵ul(t)。通過有限元計算，在ANSYS軟件的POST26后處理模塊中提取橫向支反力FWP和FWT，除以um，即可得到kdP和kdT。

ul(t)=umsin(ωt)=umsin(2πft)

(9)

式中ω、f為激勵頻率。

選取表2中的模型1，設置加載條件：fv為50mm，橫向位移激勵沿+x向加載，um為5mm，材料的阻尼比為0.05。進行頻變分析，繪制kd隨f變化曲線(簡稱kd-f曲線)，如圖6所示。當f較低時，kd基本等于靜剛度；當f位于彈簧各階橫向共振頻率附近時，kdP急劇下降，出現谷值；高于共振頻率后，kd升高并出現峰值。如此，隨著f的提高，kd的谷值、峰值交替出現，總體呈波動上升的趨勢。

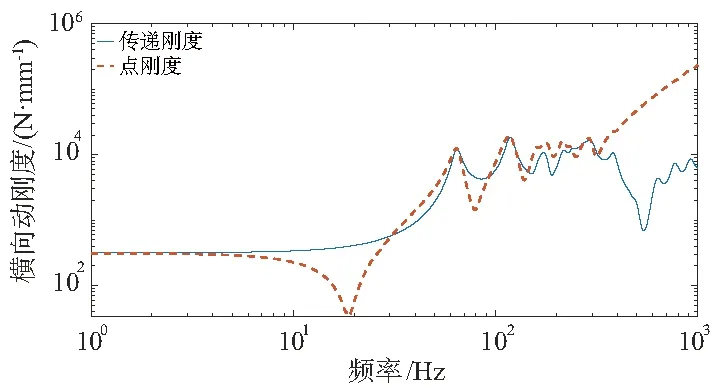
圖6 橫向動剛度隨激勵頻率變化曲線

2.2 橫向動剛度影響因素

為探究影響螺旋彈簧橫向動態傳遞特性的因素，將2.1節中的模型1設為對照組，加載條件為激勵加載方向為x軸向，垂向預壓縮量為50mm，阻尼比為0.05。每次只改變模型中的1個參數，通過有限元計算，進行頻變分析，繪制kd-f曲線。不同參數對彈簧橫向動剛度的影響效果如表4所示，表中的頻率是動剛度出現峰值和谷值點所對應的頻率。

表4 彈簧動剛度極值點放大倍數及對應激勵頻率

改變橫向激勵的加載方向，如圖7所示，發現加載方向僅影響到kd-f曲線峰值段的形狀，對橫向動剛度總體的變化趨勢并無顯著影響。

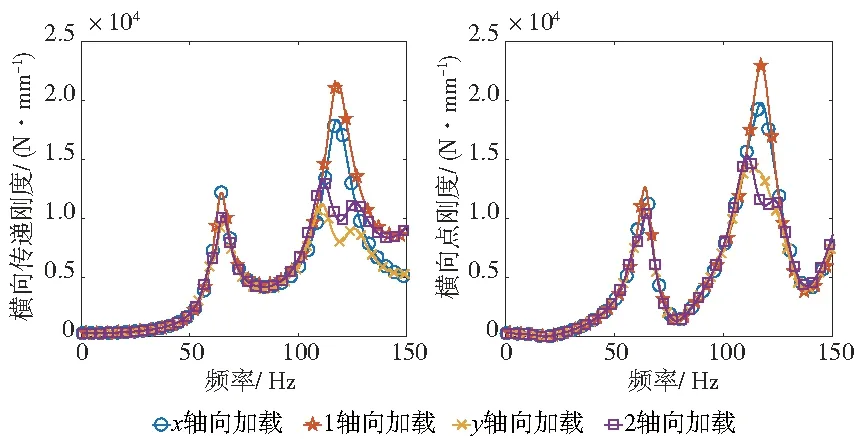
圖7 不同加載方向橫向動剛度隨激勵頻率變化曲線

改變fv為0mm(無預壓縮)和70mm的初始狀態，進行有預應力的模態分析(表5)。隨著fv的增加，各階橫向共振頻率呈逐漸減小的趨勢。施加橫向激勵，進行頻變分析，繪制不同fv下的kd-f曲線，如圖8所示。

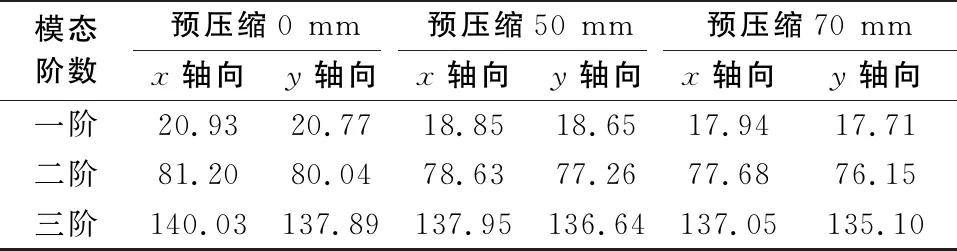
表5 不同預壓縮量彈簧橫向共振頻率 單位：Hz

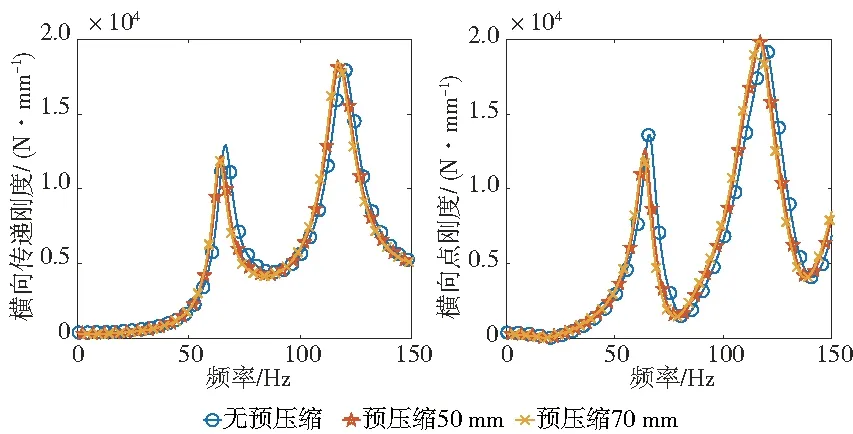
圖8 不同預壓縮量橫向動剛度隨激勵頻率變化曲線

改變激勵幅值um為10mm和20mm，進行頻變分析。發現不同um下的kd-f曲線高度重合，即激勵幅值并不會影響彈簧的動剛度特性。

改變材料的阻尼比為0.03和0.04，得到不同阻尼下的kd-f曲線，如圖9所示。隨著阻尼比的增大，kd的谷值呈不斷增大，峰值呈不斷減小的趨勢，即提高彈簧材料的阻尼可顯著降低kd的波動幅值。在小阻尼的情況下，阻尼對共振頻率無明顯影響，故阻尼比的改變并不會影響波峰、波谷所對應的激勵頻率。

圖9 不同阻尼比橫向動剛度隨激勵頻率變化曲線

3 結語

為探究等截面圓柱形螺旋壓縮彈簧橫向靜剛度及動剛度特性，建立彈簧有限元計算模型。靜載下，分析橫向載荷的大小、加載方向及垂向壓縮量對橫向靜剛度的影響，修正橫向靜剛度公式。動載下，依次改變橫向激勵的加載方向、激勵幅值、垂向預壓縮量和彈簧材料的阻尼等參數，進行頻變分析，繪制橫向動剛度隨激勵頻率變化曲線，分析橫向動剛度的影響因素。結論如下：

1) 靜載下，彈簧所受的橫向位移量和垂向壓縮量都會對橫向靜剛度產生影響，橫向靜剛度與橫向位移量呈負指數次的關系，與垂向壓縮量呈線性的關系。修正后的橫向靜剛度公式可綜合考慮上述兩個因素，計算精度和穩定性都有所提高。另外，橫向載荷的加載方向以及螺旋彈簧上、下兩切口平面的相對位置會影響橫向靜剛度的變化趨勢，在工程應用中應注意這種影響。

2) 動載下，當橫向激勵頻率等于彈簧各階共振頻率時，彈簧點剛度急劇下降，出現谷值；高于共振頻率后，動剛度升高出現峰值。如此，隨著激勵頻率的提高，螺旋彈簧橫向動剛度的谷值、峰值交替出現，總體呈波動上升的趨勢。選用阻尼比較高的彈簧材料可以顯著降低橫向動剛度的峰值，減小波動范圍。垂向預壓縮量及橫向位移激勵的幅值對橫向動剛度基本沒有影響。