平頭立銑刀端齒平面型后刀面的磨削軌跡算法

馬忠寶，唐軍，李勇，江磊

(西南交通大學(xué) 機(jī)械工程學(xué)院，四川 成都 610031)

0 引言

整體立銑刀以其良好的切削性能和幾何通用性等優(yōu)勢成為銑削加工的主要加工刀具之一。目前，已有不少針對于此的研究[1]。但隨著整體立銑刀結(jié)構(gòu)特征的復(fù)雜性和精確性要求的提高，現(xiàn)有的研究無法滿足市場需求。因此，針對整體平頭立銑刀端齒后刀面磨削方法開展研究，對提高整體立銑刀磨削精度具有十分重要的意義。

端齒部分作為整體立銑刀軸向進(jìn)給的主要切削部分，對刀具切削力和壽命影響很大[2]。端齒后刀面根據(jù)刃磨工藝不同可分為平面型和凹面型。平面型后刀面刀尖強(qiáng)度大于凹面型后刀面[3-4]，應(yīng)用更為普遍。除了端齒結(jié)構(gòu)參數(shù)的優(yōu)化設(shè)計，如何精確加工出各種特征的端齒結(jié)構(gòu)也很關(guān)鍵。針對整體立銑刀的端齒磨削加工工藝的研究也有不少。HAN L等[5]針對具有齒偏中心量和刃傾角的圓弧頭立銑刀端刃提出一種廣義的參數(shù)化建模方法，并推導(dǎo)出相應(yīng)的磨削刀位軌跡。但是用該算法加工后刀面時使用的是單錐面砂輪，不僅會使刀位的計算變復(fù)雜，在加工過程中還更容易發(fā)生干涉。另外，梁志強(qiáng)等[6]針對等法向前角和等徑向后角微細(xì)球頭銑刀的磨削提出了一套較為完整的磨削模型及機(jī)床加工的運動軌跡。該研究的體系較為完整，但是缺乏對砂輪磨削姿態(tài)進(jìn)行靈活調(diào)整的考慮。CHENG X F等[7]在球頭銑刀頂部設(shè)計了一種具有齒偏中心量的新型球頭立銑刀，并描述了“S”型刃口曲線的數(shù)學(xué)模型，然后基于該算法提出了前刀面磨削方法。

由上述研究結(jié)果可知，已有的研究對實際加工過程中干涉等問題研究相對較少，且大多采用砂輪回轉(zhuǎn)面進(jìn)行磨削，磨削質(zhì)量不高。因此，本文基于具有齒過和齒偏中心結(jié)構(gòu)特征的整體平頭立銑刀端齒刃線，提出了用于端齒平面型后刀面的磨削軌跡算法。該算法以砂輪端面為磨削面，可在保證磨削質(zhì)量的同時，通過調(diào)整砂輪擺角和抬角等工藝參數(shù)，實現(xiàn)砂輪磨削姿態(tài)定義的靈活性，避免磨削干涉。然后，結(jié)合機(jī)床的運動原理，將砂輪刀位文件轉(zhuǎn)換為五軸數(shù)控工具磨床的NC代碼，實現(xiàn)直徑10mm的整體立銑刀端齒平面型后刀面的磨削。

1 端齒直線刃相關(guān)幾何參數(shù)定義

端齒后刀面磨削軌跡算法的基礎(chǔ)是端齒直線刃幾何特征的精確描述，如圖1所示。以下對端齒直線刃的相關(guān)幾何參數(shù)進(jìn)行定義。

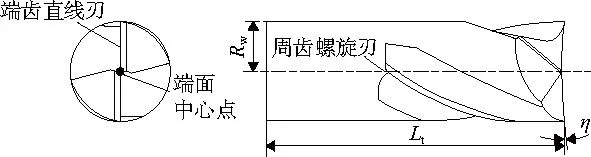
圖1 端齒直線刃相關(guān)幾何參數(shù)的定義

1) 刀刃長度Lt：定義周齒螺旋刃沿刀具回轉(zhuǎn)中心軸線方向的長度為刀刃長度Lt。

2) 刀具起始回轉(zhuǎn)半徑Rw：定義周齒螺旋刃起始處的刀具回轉(zhuǎn)體半徑為刀具起始回轉(zhuǎn)半徑Rw。

3) 螺旋角β：定義回轉(zhuǎn)體母線方向矢量與刀刃點切矢量的夾角為螺旋角β[8]。

4) 錐度角κ：定義刀具回轉(zhuǎn)體外輪廓與刀具回轉(zhuǎn)中心軸線的夾角為刀具錐度角κ。

5) 齒偏中心量h：定義端面中心點到端齒直線刃的距離為齒偏中心量(或稱作偏心距)h。

6) 齒過中心量lh：定義端齒直線刃沿其刃線方向超出端面中心點的距離為齒過中心量lh。

7) 端齒直線刃內(nèi)傾角η：定義端齒直線刃與垂直于刀具回轉(zhuǎn)軸線平面的夾角為內(nèi)傾角η。

8) 端齒回轉(zhuǎn)半徑r：定義刀具端齒部分刀體回轉(zhuǎn)半徑為r。根據(jù)周齒錐角的幾何關(guān)系，可得

r=Rw-Lt·tanκ

(1)

9) 端齒直線刃的長度Lh：定義端齒直線刃的長度為Lh。根據(jù)直線刃的空間幾何關(guān)系，可得

(2)

2 坐標(biāo)系定義

2.1 工件坐標(biāo)系

立銑刀砂輪磨削軌跡研究的目標(biāo)是獲得磨削過程中機(jī)床各軸在任意時刻的位置。為了便于立銑刀數(shù)控磨削的對刀和得到控制機(jī)床的NC程序，需要將磨削坐標(biāo)系下的磨削軌跡變換到工件坐標(biāo)系Ow-xwywzw對其進(jìn)行描述。定義刀具回轉(zhuǎn)軸為zw軸，以周齒螺旋刃線起點所在端面為xwOwyw平面，如圖2所示。

圖2 工件坐標(biāo)系及端齒坐標(biāo)系位置示意圖

定義周齒螺旋刃線末點(端齒直線刃起點)處，相對于工件坐標(biāo)系x軸繞z軸的旋轉(zhuǎn)角為回轉(zhuǎn)角φz。等螺旋角的圓柱型和圓錐型刀具周齒刃線的相關(guān)研究已經(jīng)相對完善[8]，本文采用文獻(xiàn)[9]中推導(dǎo)周齒刃線過程中用到的回轉(zhuǎn)角φz的推導(dǎo)公式，如式(3)所示。

(3)

式中φ0為初始回轉(zhuǎn)角[9]。

2.2 端齒坐標(biāo)系

為了便于端齒刃線的表達(dá)，定義端齒坐標(biāo)系Od-xdydzd。端齒坐標(biāo)系可由工件坐標(biāo)系繞z軸旋轉(zhuǎn)回轉(zhuǎn)角φz，再沿z軸正方向平移Lt得到，如圖2所示。

本文采用變換矩陣的方式描述任意一點從端齒坐標(biāo)系下的坐標(biāo)P′轉(zhuǎn)換到工件坐標(biāo)系下坐標(biāo)P的變換關(guān)系，如式(4)所示。

P=Md-w·P′+Td-w

(4)

式中:Md-w表示從端齒坐標(biāo)系到工件坐標(biāo)系的旋轉(zhuǎn)矩陣，

(5)

Td-w表示從端齒坐標(biāo)系到工件坐標(biāo)系的平移矩陣，

(6)

2.3 直線刃坐標(biāo)系

為了便于直線刃后刀面的定義，定義直線刃坐標(biāo)系Om-xmymzm。直線刃坐標(biāo)系(圖3)是由端齒坐標(biāo)系繞z軸相對回轉(zhuǎn)角反向旋轉(zhuǎn)一個角度φzh，再繞y軸旋轉(zhuǎn)一個角度θ，最后沿著x軸正方向平移r得到的。

(7)

(8)

圖3 直線刃坐標(biāo)系示意圖

同理，定義任意一點從直線刃坐標(biāo)系下的坐標(biāo)P′轉(zhuǎn)換到端齒坐標(biāo)系下的坐標(biāo)P變換關(guān)系如下式：

P=Mm-d·P′+Tm-d

(9)

式中：Mm-d表示從直線刃坐標(biāo)系到端齒坐標(biāo)系的旋轉(zhuǎn)矩陣，

(10)

Tm-d表示從直線刃坐標(biāo)系到端齒坐標(biāo)系的平移矩陣，

(11)

3 端齒直線刃定義

3.1 端齒后刀面寬度和后角

端齒直線刃后刀面的定義基于直線刃坐標(biāo)系。端齒后刀面寬度和后角都以xmym平面為基準(zhǔn)，如圖4所示。定義P0點為端齒直線刃的起點，P0P1為第一后刀面與xmym平面的交線，l為第一后刀面寬度；λ為第一后角。

圖4 端齒后刀面寬度與角度示意圖

P0點在直線刃坐標(biāo)系的坐標(biāo)為P0(0，0，0)，則由圖4所示的幾何關(guān)系可知P1點坐標(biāo)可表達(dá)如下：

(12)

3.2 端齒直線刃單位矢量

設(shè)端齒直線刃起點P0處端齒直線刃的單位切矢量為Fxw，則

(13)

從而，端齒直線刃上的任意點Pt坐標(biāo)可以表示為

Pt=t·Fxw+P0，0≤t≤Lh

(14)

4 砂輪軌跡計算

4.1 砂輪初始姿態(tài)

本文采用砂輪端平面磨削的方式，當(dāng)砂輪為初始姿態(tài)時，砂輪端平面與端齒后刀面重合。砂輪姿態(tài)的定義都基于直線刃坐標(biāo)系。

定義P0指向P1的矢量為Ft，則Ft垂直于Fxw，且Ft和Fxw構(gòu)成的平面與砂輪初始姿態(tài)下的砂輪端面重合。定義此平面的法矢為砂輪軸矢量Fg：

Fg=Ft×Fxw

(15)

圖5 砂輪初始姿態(tài)示意圖

定義P0指向砂輪磨削端面圓中點Og(刀位點)的矢量為Fb，砂輪大端面在P0點與矢量Ft相切。由于Fb垂直于Fg與Ft，可得

Fb=Fg×Ft

(16)

因此只要將P0沿著矢量Fb方向移動砂輪端面半徑Rg的距離，即可得到刀位點坐標(biāo)：

Og=P0+Rg·Fb

(17)

4.2 砂輪擺角工藝參數(shù)對初始姿態(tài)的變換

為了避免在后刀面磨削過程中可能產(chǎn)生的砂輪與端齒其他特征結(jié)構(gòu)的干涉，在直線刃坐標(biāo)系中引入砂輪擺角工藝參數(shù)。定義端齒后刀面在P0點的法矢量為Fg0(圖6)，則在直線刃坐標(biāo)系下

(18)

圖6 矢量Fg0示意圖

定義擺角μag為砂輪以P0為中心，以矢量Fg0為回轉(zhuǎn)軸所旋轉(zhuǎn)的角度，如圖7所示。

圖7 砂輪擺角示意圖

已知繞空間任一單位矢量N(Nx，Ny，Nz)旋轉(zhuǎn)一個角度γ的旋轉(zhuǎn)矩陣通式為：

Rot(N，γ)=

(19)

式中versγ=1-cosγ。

則點P1繞矢量Fg0旋轉(zhuǎn)擺角μαg得到點P′1，其表達(dá)式如下：

P′1=Rot(Fg0，μαg)P1

(20)

由點P′1和點P0得到矢量F′t，根據(jù)式(15)-式(17)，可得具有擺角的砂輪軸矢F′g和刀位點坐標(biāo)O′g。

4.3 砂輪抬角工藝參數(shù)對初始姿態(tài)的變換

定義抬角δαg為砂輪繞經(jīng)過擺角變換后的矢量F′t所旋轉(zhuǎn)的角度，如圖8所示。

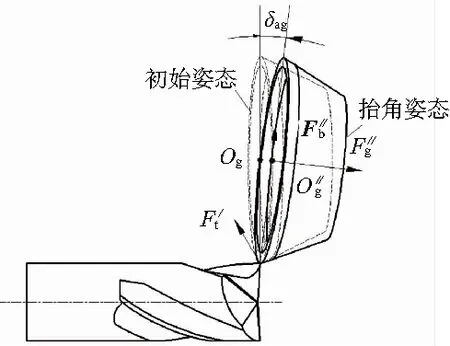
圖8 砂輪抬角示意圖

直線刃坐標(biāo)系下，定義F″g為經(jīng)過抬角變換的砂輪軸矢量，其可由F′g繞F′t旋轉(zhuǎn)δαg得到

F″g=Rot(F′t，δαg)F′g

(21)

進(jìn)一步根據(jù)式(15)-式(17)，可得具有抬角的砂輪刀位點坐標(biāo)O″g。

4.4 砂輪在工件坐標(biāo)系下軌跡描述

由上述得到的刀位點坐標(biāo)和砂輪軸矢量并結(jié)合式(14)，可得到端齒直線刃任意點Pt對應(yīng)的刀位點坐標(biāo)和砂輪軸矢量。再通過一系列坐標(biāo)轉(zhuǎn)換，最終轉(zhuǎn)換到工件坐標(biāo)系下的表達(dá)式。轉(zhuǎn)換矩陣如式(22)、式(23)所示，其中Og_w為刀位點坐標(biāo)，F(xiàn)g_w為砂輪軸矢量。

(22)

(23)

5 磨床磨削運動量計算

本文采用國產(chǎn)精利MD3015五軸聯(lián)動數(shù)控工具磨床進(jìn)行刃磨加工。該機(jī)床的拓?fù)溥\動結(jié)構(gòu)為ACYFXZ型，屬工件雙擺動類型五軸機(jī)床，其結(jié)構(gòu)和運動形式如圖9所示。砂輪組配置如圖10(a)所示，由1V1型、1A1型和11V9型3片砂輪組成。其中，11V9型砂輪用于制造整體式平頭立銑刀的端齒后刀面部分，并且選擇砂輪端面Ⅰ作為端面進(jìn)行后刀面刃磨。另外兩個砂輪用于加工整體式平頭立銑刀的其他部分。

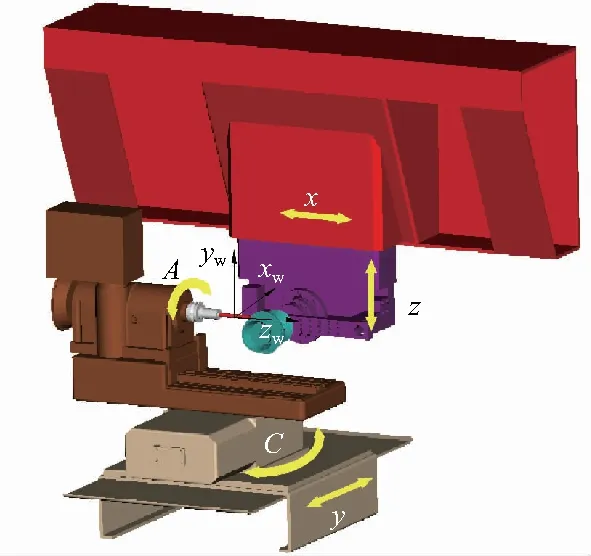
圖9 MD3015型五軸數(shù)控工具磨床運動形式

圖10 砂輪軸上砂輪配置及碗型砂輪形狀

結(jié)合實際加工需求，建立兩個對刀點(主軸對刀點PZ和夾頭對刀點PD)。兩個對刀點的位置如圖10(a)所示，分別位于主軸和夾頭的端面中心處。結(jié)合五軸數(shù)控后置處理算法的研究[10]，定義A、C、Sx、Sy和Sz為磨削過程中機(jī)床A、C、x、y和z軸相對對刀點的運動角度和距離值，可得到描述工件坐標(biāo)系下的砂輪軌跡坐標(biāo)與機(jī)床各軸運動位置的轉(zhuǎn)換關(guān)系：

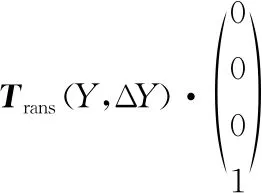
(24)

(25)

式中：ΔX為夾頭對刀點PD偏離C軸回轉(zhuǎn)軸的投影距離；ΔY為砂輪安裝面相對主軸對刀點PZ的y向距離;ΔL為夾頭對刀點PD相對工件坐標(biāo)系原點的x向距離。

整體立平頭立銑刀端齒第二后刀面的刃磨方法與主后刀面類似，并且需要指出的是，主后刀面的寬度是通過控制第二后刀面刃磨過程實現(xiàn)的。

6 試驗驗證

基于本文所提出的磨削軌跡算法，利用VC++環(huán)境開發(fā)了一套算法程序模塊，輸入相關(guān)工藝參數(shù)以后，按照一定步長循環(huán)計算即可獲得理論端齒刃線所對應(yīng)的砂輪磨削數(shù)控程序。將NC程序?qū)隫ericut仿真軟件，進(jìn)行磨削仿真并檢查干涉情況。端齒后刀面磨削仿真結(jié)果如圖11所示。

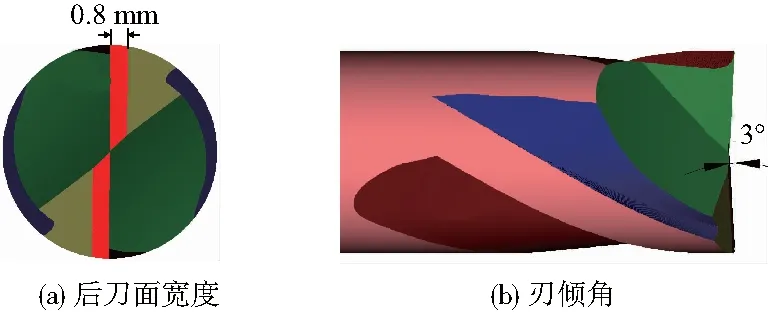
圖11 仿真結(jié)果

實際磨削過程如圖12所示。砂輪轉(zhuǎn)速為25m/s，進(jìn)給速度為10mm/s，磨削過程采用磨削油冷卻。

圖12 實際磨削加工過程

在保持相同工藝參數(shù)和數(shù)控程序條件下，連續(xù)磨削3把整體平頭立銑刀，利用刀具檢測儀PG-1000分別對磨削后的3把立銑刀的幾何參數(shù)進(jìn)行觀測，如圖13所示。對端齒后刀面的后角、主后刀面寬度和端齒向心角進(jìn)行測量，測量結(jié)果如表1所示。刀具參數(shù)誤差在3%以內(nèi)，與設(shè)計值具有較高的吻合度，且經(jīng)過砂輪抬角及擺角的微調(diào)，磨削過程并未出現(xiàn)干涉情況。

圖13 實際磨削得到整體式平頭立銑刀端齒部分

7 結(jié)語

1) 提出了以砂輪端面為磨削面的端齒平面型后刀面的磨削軌跡算法，可在保證磨削質(zhì)量的同時，通過調(diào)整砂輪擺角和抬角等工藝參數(shù)，實現(xiàn)砂輪磨削姿態(tài)定義的靈活性，避免干涉。

表1 立銑刀端齒后刀面幾何參數(shù)設(shè)計值與實測值

2) 基于五軸數(shù)控工具磨床的運動原理推導(dǎo)出機(jī)床各軸運動位置與工件坐標(biāo)系坐標(biāo)的轉(zhuǎn)換關(guān)系，計算了磨床的進(jìn)給運動量。