齒輪傳動系統傳動軸模態仿真及振動實驗測試研究

王冰

(煙臺汽車工程職業學院，山東 煙臺 265500)

0 引言

當前，齒輪傳動結構被廣泛應用于車輛動力系統、減速機等領域，已經成為工業制造過程的一項必不可少的組成部分[1-3]。由于齒輪在實際運行過程中受到各類外部因素的綜合影響，使其運行狀態發生變化，無法獲得精確的加工尺寸，嚴重時還會引起齒輪傳動故障的問題。由于采用現有技術還無法對故障信號進行準確分析，在系統運行過程中，傳動軸振動狀態會降低系統的穩定性[4-5]。為了便于對上述不確定性因素進行分析，許多學者在構建模型的過程中都進行了適當簡化處理，再利用動力學計算的方法得到最終結果。采用上述處理方法對齒輪結構和系統性能進行分析，最后對設計方案進行優化并分析了系統的運行可靠性[6-7]。

根據前期文獻關于齒輪結構傳動軸的動力學研究內容可知，已有許多學者開發了多種計算方法，主要包括時域法、代數分析法等。采用微分處理方法對系統運動過程進行了行動力學分析，同時建立了相應的傳遞函數[8-9]。同時也可以選擇不同的方法來完成求解計算。其中，時域方法可以對系統中各零部件在不同時域條件下的時變動態參數進行分析，以頻域法進行處理時則可以得到各項系統參數在每種頻域條件下的具體狀況。此外，齒輪運行狀態還會受到時變嚙合剛度以及實際尺寸精度參數的綜合影響，因此在各個時間段中發生了周期性激勵變化的現象，采用時域處理方法也表現出了同樣的周期性響應特征[10]。以上研究結果表明，可以通過分析研究對象發生的時域和頻域變化狀態，實現對系統響應頻率的精確分析，同時建立得到更加準確的激勵、響應關系。

1 模態疊加模型建立

對多自由度系統進行分析的過程中，還應將黏性阻尼的因素也考慮在內，采用以下微分方程表示系統受迫振動的運動形式：

(1)

式中：M、C、K為對角矩陣；F為受迫振動力。將對角線元素表示成如下矢量形式：

(2)

式(2)是在n自由度下對應的運動方程，根據振動理論進行計算。

(3)

其中：hi(τ)是單位脈沖響應函數。其表達式為

(4)

式(4)是多自由度系統受到激振力作用的情況下出現的響應結果，并且各階模態都會對激振力造成不同程度的作用。

2 傳動軸模態分析

2.1 傳動軸模態建立

本文研究的齒輪傳動結構由四級減速系統構成，具體傳動結構見圖1。行星輪處于低速傳動的狀態下時，通過傳動軸進行輸出，需要同時承受輸入軸與負載形成的轉矩作用。當傳動軸結構發生變形時，傳統系統的內部結構難以精確嚙合，導致齒輪箱運行過程出現故障。根據以上研究結果，為了對系統振動狀態開展更加深入的分析，避免發生共振的問題，對傳動軸模態差異性和振型特點進行了研究，同時確認是否因為共振的問題而引起行星齒輪運行過程出現異常。圖2為模態分析的具體過程。

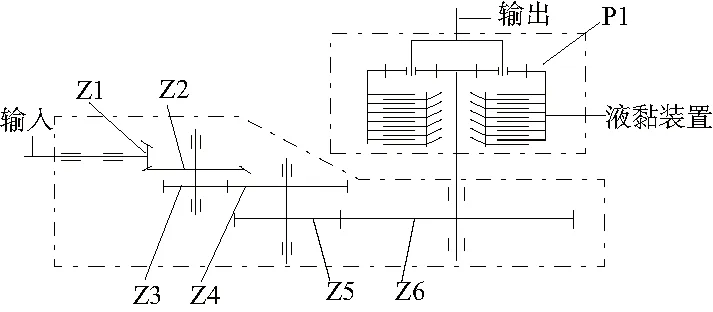
圖1 齒輪傳動系統結構組成示意圖

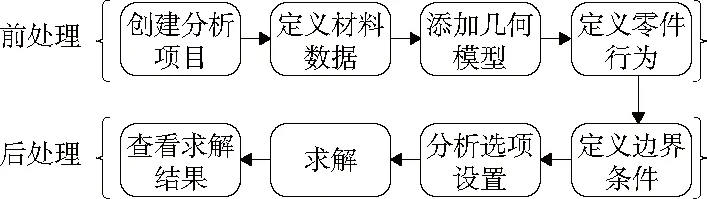
圖2 模態分析流程

采用QT500傳動軸作為測試對象，傳動軸輸出通過軸承進行支撐，依次設置了Cylindrical Support和Displacement兩種約束方式。

2.2 傳動軸模態結果分析

以Modal 模塊對傳動軸結構進行仿真測試。對圖3進行分析可以發現，在6階模態下分析時，傳動軸出現了局部扭轉和振動的結果，提高模態階數的過程中，振型變得更明顯。其中，前2階模態只沿某一特定的方向發生了變形，但3-6階模態發生了扭轉。

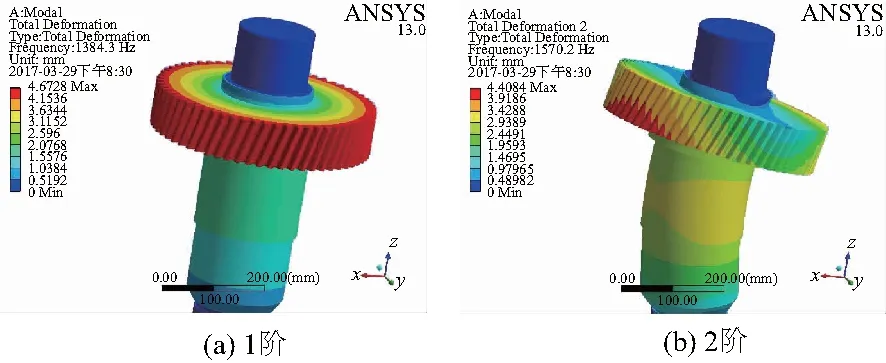
圖3 傳動軸模態變形云圖

為實現齒輪傳動系統的安全穩定運行過程，需選擇抗振性優異的傳動軸。本文研究的傳動軸由四級減速結構組成，同時建立模態疊加模型，對傳動軸模態特征進行了分析，之后測試了軸承振動和加速度參數。表1對應前6階模態傳動軸的固有頻率分布結果。對前6階模態頻率以及振型參數進行分析可知，傳動軸發生了局部振動并存在扭轉的現象，當模態階數增大后，獲得了更明顯振型。傳動軸前6階頻率介于625～1339Hz之間，并且最低固有頻率也大于最高嚙合頻率，從而避免了齒輪箱與傳動軸發生共振的問題。采用MED分解加速度振動信號，得到前2階IMF分量，再通過切片雙譜測試減小模態混疊程度，達到信號數據簡化的效果，以上測試結果表明，可以通過實驗分析過程設計傳動軸結構。

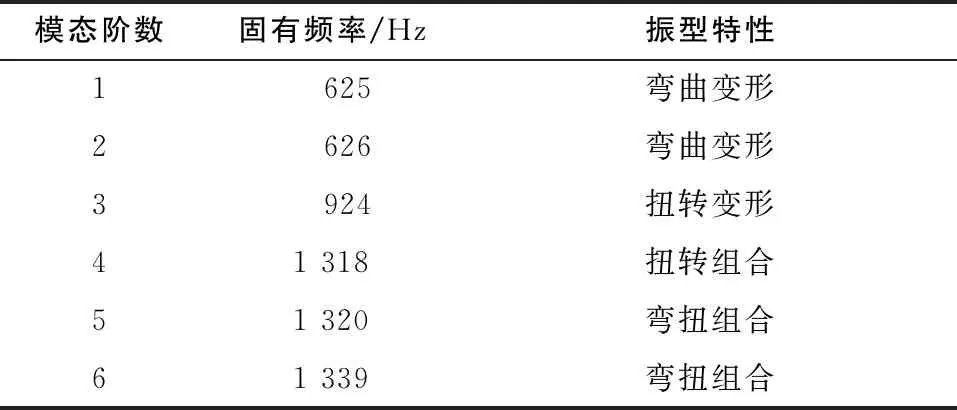
表1 對應前6階模態傳動軸的固有頻率分布

對表1測試結果進行分析可知，隨著模態階數的增加，頻率也發生了增大。傳動軸的前6階固有頻率介于610～1324Hz之間，齒輪系統轉頻介于1.3～581.3Hz之間，經對比發現，傳動軸最低固有頻率已經超過最高嚙合頻率，因此可以避免齒輪箱與傳動軸出現共振的情況。

3 傳動軸振動試驗

選擇四級減速結構作為測試平臺，圖4為測試平臺組成結構。齒輪傳動比等于1∶1，保持1 200 r/min的轉速，以12 000 Hz的頻率進行采樣，按照逐級方式完成載荷的加載過程，逐漸提高負載到800 Nm，使用CA-YD-186壓電傳感器。利用MED對傳動軸振動信號進行處理。仿真數據如圖5所示。

1—調速電機；2—聯軸器；3—傳動齒輪箱；4—轉速儀；5—扭力桿；6/7/8/9—壓電式加速傳感器；10—試驗齒輪箱。圖4 齒輪傳動試驗臺

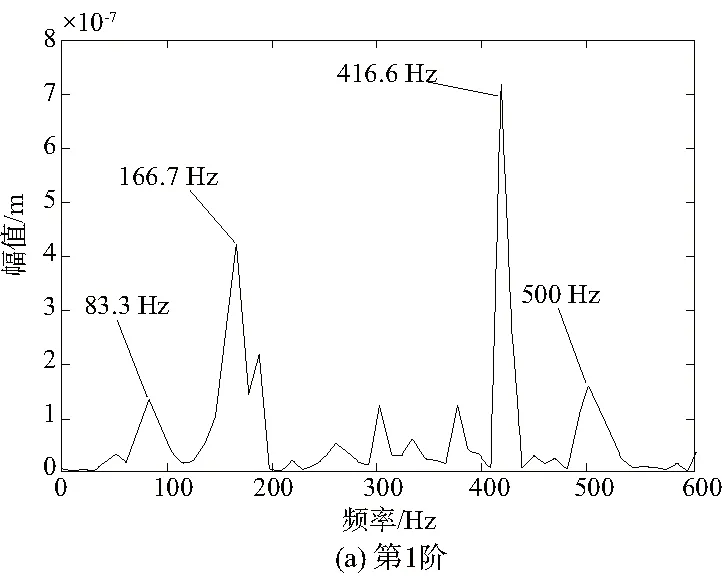
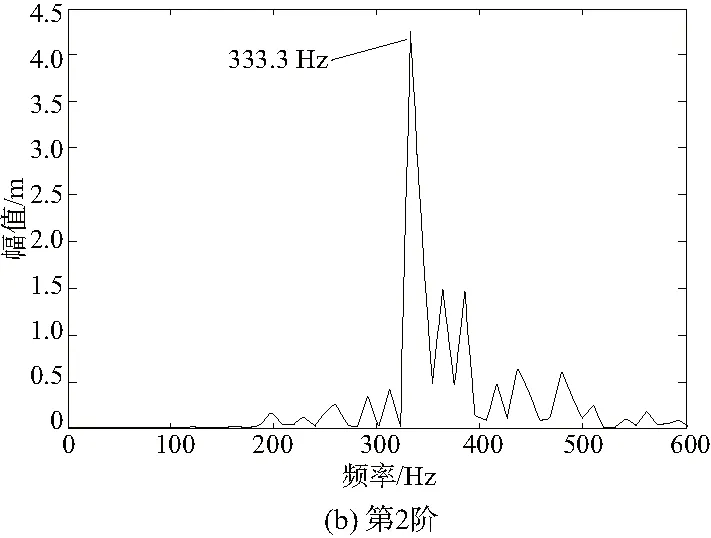
圖5 齒輪振動信號前2階IMF分量經MED分解后進行切片雙譜分析

從圖5中可以看到,通過MED對仿真數據進行處理獲得的最初2階IMF分量，之后進行切片雙譜分析，從圖5(a)中可以發現，低頻部分形成了故障頻率等于360Hz的一倍、二倍頻，同時獲得了更明顯的三倍、四倍頻，根據以上分析可以判斷采用上述方法能夠大幅降低高斯噪聲導致的低頻弱故障概率。圖5(b)顯示形成了更顯著的三倍頻1080Hz和四倍頻1440Hz，減少了模態混疊影響，獲得了更加清晰簡易的信號數據。由此可見，利用本文方法進行設計獲得的傳動軸滿足使用要求。

4 結語

1) 傳動軸發生了局部振動并存在扭轉，當模態階數增大后，獲得了更明顯振型。傳動軸前6階頻率介于625～1339Hz之間，并且最低固有頻率也大于最高嚙合頻率，從而避免了齒輪箱與傳動軸發生共振的問題。

2) 低頻部分形成了故障頻率等于360Hz的一倍、二倍頻，同時獲得了更明顯的三倍、四倍頻，可以判斷本文方法能夠大幅降低高斯噪聲導致的低頻弱故障概率。利用本文方法進行設計獲得的傳動軸滿足使用要求。