基于ρ-支配輪廓及n-of-Nρ-支配輪廓的數據流中關鍵數據計算方法
霸建民,郭永紅,彭龍,趙東陽,邵鵬志,杜宏博
(中國兵器工業集團有限公司 計算機應用技術研究所,北京 100089)
0 引言
目前,隨著數據采集手段的迅猛發展,大量的數據得以產生并且呈現出數據流[1-2]的特點。但是很多情況下數據采集區域的網絡非常受限,比如網絡時斷時續、網絡帶寬較小,而且數據應用和數據采集往往分布在不同的地點,因此怎樣將采集的流式數據及時傳輸到數據應用方至關重要。例如,裝甲車通過傳感器能夠實時獲取車輛的油壓、水溫等狀態數據,而遠方的數據中心通過這些車輛的狀態數據可以判斷出車輛的健康狀況,指揮官根據車輛的健康狀況進行某場戰役的指揮,因此在網絡受限情況下,如何計算出車輛狀態數據中的關鍵數據進行傳輸至關重要。
作為多目標決策與數據挖掘的重要手段之一,輪廓查詢[3-5]及其變體輪廓查詢[6-18]在許多實際應用中都發揮著非常重要的作用,即從海量數據中選取最為關鍵的數據。給定一個多維元組的集合P,則元組P的輪廓指的是P中所有不被其他多維元組支配的元組集合。一個多維元組x支配另一個多維元組y等價于元組x在所有維度上都不比元組y差并且至少在某個維度上元組x比元組y關鍵。數據元組在各維度上的關鍵與否,可以是用戶指定的標準,即可以是“大于”、“小于”以及“不等于”等。
當以“小于”作為關鍵的標準進行輪廓查詢時,查詢的結果為偏向給定查詢點q的數據,此種情況下可以被應用于個性化商品推薦,將輪廓結果反饋給用戶。但是由于裝甲車狀態數據中查詢偏向給定查詢點的狀態數據,在數據中心接收到的為最接近查詢點q的狀態數據,而存在健康問題的狀態數據不能通過輪廓查詢算法計算出來發送給數據中心,因此數據中心無法判斷哪些裝甲車輛存在問題。而當采用“大于”作為關鍵的標準時,輪廓計算出的數據為偏離查詢點的數據,即為相對異常的數據,數據中心能夠憑借異常數據鑒定裝甲車輛的健康狀況。鑒于此,本文采用“大于”作為關鍵的標準。以“大于”作為標準和以“小于”作為標準對輪廓的影響如圖1所示。

圖1 關鍵標準對輪廓的影響Fig.1 Effect of key standards on skyline
傳統輪廓查詢中的支配關系都是依賴于多維數據對應數值之間的大小關系而進行設計的,均沒有考慮數值間的比例關系。然而,在一些實際應用中,數值間的大小關系并不能完全說明兩組數據誰更關鍵,這時就需要使用數值間的比例關系進行關鍵數據選擇。例如,某型裝甲車的標準油壓和水溫為20 kPa和20 ℃,而某一個裝甲車有兩組狀態數據在油壓和水溫之外其他的狀態數據都一樣,其中狀態A油壓為40 kPa、水溫為30 ℃,狀態B油壓為45 kPa、水溫為25 ℃,要求從狀態A和狀態B中選出關鍵的數據傳送到數據中心。狀態A在油壓和水溫上偏離標準狀態的偏離值分別為20 kPa和10 ℃,狀態B在油壓和水溫上偏離標準狀態的偏離值分別為25 kPa和5 ℃,當考慮數值間大小關系時,在油壓維度上狀態A的偏離值比狀態B的偏離值小5 kPa,而在水溫維度上狀態A的偏離值比狀態B的偏離值大5 ℃,因此不能決定狀態A和狀態B哪個更關鍵。這時可以考慮基于數值間比例的支配關系,在油壓維度上狀態A的偏離值與狀態B的偏離值的比值為0.8,在水溫維度上狀態A的偏離值與狀態B的偏離值的比值為2,因此在兩維上的比值均≥0.8;在油壓維度上狀態B的偏離值與狀態A的偏離值的比值為1.25,在水溫維度上狀態B的偏離值與狀態A的偏離值的比值為0.5,不均≥0.8,因此可以判定狀態A更關鍵。特別是當各維度上數值不在同一量級時,基于對應數值間比例的支配關系更能計算出關鍵數據。將對應數值間的比值稱之為ρ,因此基于對應數值間比例的支配關系也稱之為ρ-支配關系,在此基礎上的輪廓查詢稱之為ρ-支配輪廓[19]查詢。
然而,裝甲車輛的狀態數據具有數據流的特性,王之瓊等[20]在ρ≥1時,以“小于”作為關鍵的標準討論了ρ-支配關系的性質,并且給出了一種數據流中ρ-支配輪廓計算方法。本文考慮網絡受限環境中裝甲車輛狀態數據傳輸的實際情況,偏離查詢點的狀態數據對于評估裝甲車輛的健康狀態更為關鍵,因此以“大于”作為關鍵的標準進行分析,然而當以“大于”作為關鍵的標準時,ρ-支配關系的性質將發生改變,原算法不能直接應用于以“大于”作為關鍵標準的數據流中ρ-支配輪廓查詢,同時考慮ρ≥1以及ρ<1的不同情況,對ρ-支配關系的性質重新進行分析,進而對原算法進行更改及擴展,在此基礎上提出了數據流中n-of-Nρ-支配輪廓查詢算法,數據流中n-of-Nρ-支配輪廓查詢算法是在滑動窗口(大小為N)最近的n(n≤N)個點中計算ρ-支配輪廓點,進一步滿足網絡受限環境中關鍵數據選擇傳輸的要求。歸結起來,本文的主要貢獻如下:
1) 以“大于”作為關鍵的標準,同時考慮ρ≥1以及ρ<1的不同情況重新對ρ-支配關系和ρ-支配輪廓的定義和性質進行了分析;
2) 對數據流中ρ-支配輪廓查詢算法進行更改及擴展,在此基礎上提出了數據流中n-of-Nρ-支配輪廓查詢算法;
3) 設計了詳盡的實驗,通過實驗表明數據流中n-of-Nρ-支配輪廓查詢相比于數據流中ρ-支配輪廓查詢具有更廣泛的應用。
1 相關研究工作
一些學者在傳統輪廓查詢的基礎上提出了輪廓變體查詢:Borzsonyi等[3]使用輪廓查詢去擴展數據庫系統,輪廓操作從一組大數據集合中篩選出一組用戶所感興趣的子數據集合,并提出了嵌套循環算法;Papadias等[4]分析了NN算法的缺陷并提出了BBS算法,此算法采用鄰近漸進搜索方式,僅對可能包含輪廓點的R樹節點執行單次訪問;Ding等[5]提出了在Map-Reduce框架下處理海量數據的輪廓查詢算法,另外給出了高效的優化方法用來提高海量數據輪廓查詢的效率;Lai等[7]研究了移動物聯網應用中特定范圍內的RSQ算法,提出了一種有效、非集中的分布式DCRSQ算法,以滿足移動環境中的范圍輪廓查詢的需求;Tian等[8]針對高維數據集合中計算輪廓時檢索數據量大的問題,提出了一種在MapReduce框架下的并行k-維輪廓查詢算法,提高了k-維輪廓查詢的效率;Chen等[13]考慮到現實中的數據具有動態性,將輪廓查詢擴展到變換空間中,提出了變換空間中的輪廓查詢,并提出了一種剪枝技術提高變換空間中輪廓查詢的效率;周劍剛等[14]提出了一種道路網的輪廓查詢EI算法,通過分析用戶運動狀態與查詢間的關聯關系,根據時間通過協同過濾擴展方法確定初始輪廓結果集,并對數據集進行剪枝,監測用戶的運動狀態,一旦用戶速度發生變化,就快速根據出入點信息動態調整輪廓集;Zou等[15]研究了大型圖表中的動態skyline查詢,并提出了一種基于圖屬性的修剪規則,以推導DSG查詢的候選對象;Li等[16]提出了一種基于多層網格模型的數據流中動態輪廓查詢方法,模型將工作空間劃分為多層網格,并基于現有數據集創建每層網格的skyline影響區域,僅當動態數據點在每層網格的skyline影響區域內更新時,才進行連續skyline查詢;張麗等[17]為了應對元組在數據流上隨機添加和刪除的挑戰,采用了基于網格的索引來存儲元組,并提出了一種基于該索引的算法來計算和維護輪廓集;Bai等[18]提出了一種改進的基于數據流的動態輪廓查詢算法IDS2,避免在更新某些點時計算量急劇增加,加快數據流上更新操作的速度,提高動態skyline的計算性能。
也有學者針對ρ-支配輪廓查詢開展了一些研究工作。信俊昌等[19]首先通過對實際應用需求進行分析,提出了基于數值間比例值大小的ρ-支配關系,并且根據ρ-支配關系提出了ρ-支配輪廓查詢,進一步提出了計算ρ-支配輪廓的BA算法和基于分支定界的BBDS算法,最后通過實驗證明了BBDS算法相比于BA算法提升了效率;王之瓊等[20]在ρ≥1時,以“小于”作為關鍵的標準給出了完全支配、ρ-支配以及ρ-支配輪廓的定義,進一步給出了數據流中ρ-支配輪廓的定義,然后分析了數據流中ρ-支配輪廓的性質并提出了基于時序支配的數據過濾方法,最后給出了數據流中ρ-支配輪廓查詢的DSSW算法,將ρ-支配輪廓計算方法擴展到數據流中。
2 ρ-支配理論
數據流中ρ-支配輪廓查詢算法[20]以“小于”作為關鍵的標準給出了完全支配和ρ-支配的定義,本文為了解決裝甲車輛狀態數據中關鍵數據選擇傳輸的需要,以“大于”作為關鍵的標準重新給出相關定義。
定義1(完全支配) 一個多維數據點x關于查詢點q完全支配另一個多維數據點y當且僅當滿足以下兩個條件:
?i∈[1,d],(x[i]-q[i])(y[i]-q[i])≥
0∧|x[i]-q[i]|≥|y[i]-q[i]|,
(1)
?i∈[1,d],(x[i]-q[i])(y[i]-q[i])>
0∧|x[i]-q[i]|>|y[i]-q[i]|,
(2)
式中:d為數據的維度。
定義2(ρ-支配) 一個多維數據點x關于查詢點qρ-支配另一個多維數據點y當且僅當滿足以下兩個條件:
?i∈[1,d],(x[i]-q[i])(y[i]-q[i])≥
0∧|x[i]-q[i]|≥ρ×|y[i]-q[i]|,
(3)
?i∈[1,d],(x[i]-q[i])(y[i]-q[i])>
0∧|x[i]-q[i]|>ρ×|y[i]-q[i]|.
(4)
由定義1和定義2可以看出,以“大于”作為關鍵的標準時完全支配和ρ-支配的定義與以“小于”作為關鍵的標準時完全支配和ρ-支配的定義有所不同,所滿足的條件由“小于”和“小于等于”變為了“大于”和“大于等于”。
圖2為二維空間中完全支配和ρ-支配的示意圖。圖2(a)是完全支配的一個例子,其中:由于數據點a和數據點b在以點q為中心的同一象限內,并且在任意維度上數據點a和點q間的長度都大于數據點b和點q間的長度,所以點a關于查詢點q完全支配點b.圖2(b)展示了當ρ=2時的ρ-支配關系示例,其中:點a′是點a和點q的中點,點b′是點b和點q的中點;由于數據點a和數據點b在以點q為中心的同一象限內并且點a′與點q的距離并不在任意維度上都大于等于點b與點q的距離,因此點a不能ρ-支配點b,同理點b不能ρ-支配點a.從上述分析中可以看出,當ρ改變時,相同數據集合的ρ-支配關系將發生改變。

圖2 完全支配和ρ-支配Fig.2 Full dominance and ρ-dominance
定義3(數據流中ρ-支配輪廓[20]) 給定一個數據流P、滑動窗口大小N和一個查詢點q,則數據流上位于滑動窗口的數據集PN中不被其他任何點ρ-支配的點構成數據流中ρ-支配輪廓。
定義4(數據流中n-of-Nρ-支配輪廓) 給定一個數據流P、滑動窗口大小N和一個查詢點q,則滑動窗口PN中最近的n(n≤N)個點中不被滑動窗口中其他任何點關于查詢點qρ-支配的點構成數據流中n-of-Nρ-支配輪廓。
數據流中最近的N組多維數據點即為滑動窗口中的點,而最近的n組多維數據點為滑動窗口中的部分點。由定義4可知,數據流中n-of-Nρ-支配輪廓點只可能在滑動窗口中最近的n組數據點中產生,因此可以將滑動窗口中的N個數據點分為兩部分。如圖3所示,其中編號[N-n+1,N]的數據點是最近的n組數據點稱為有效部分,編號[1,N-n]的數據點為其余N-n組數據點稱為無效部分。對于一個剛剛到達滑動窗口的數據點p來說,由于點p為最近的一個點,所以點p一定位于滑動窗口的有效部分。由定義3和定義4可以看出,數據流中ρ-支配輪廓是數據流中n-of-Nρ-支配輪廓當n=N時的特例。另一種特例為n=1時,代表的是僅僅考慮最新的數據點是否為關鍵數據,如果是則傳輸給數據應用方,如果不是則不傳輸。因此數據流中n-of-Nρ-支配輪廓是數據流中ρ-支配輪廓的擴展,相比于ρ-支配輪廓擁有更廣泛的應用。
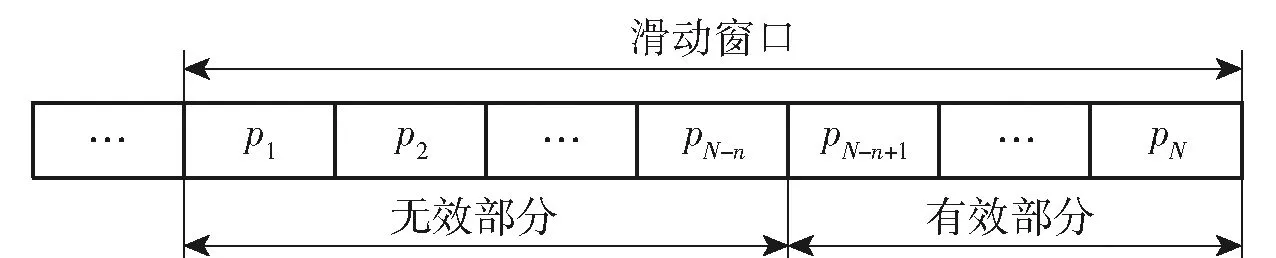
圖3 n-of-N中滑動窗口劃分Fig.3 Partition of sliding window in n-of-N
由于王之瓊等[20]給出的ρ-支配關系的性質是在ρ≥1時并且以“小于”作為關鍵的標準來進行的,因此不適用于本文的相關研究。本文以“大于”為關鍵的標準并且在ρ>0時重新對ρ-支配關系的性質進行討論。
定理1給定兩個值ρ1和ρ2并且ρ1<ρ2,如果一個多維數據點p是ρ1-支配輪廓點,那么點p一定也是ρ2-支配輪廓點。
證明:定理1采用反證法,假設點p不是ρ2-支配輪廓點,則存在另一點xρ2-支配點p,根據定義2可得
?i∈[1,d],(x[i]-q[i])(p[i]-q[i])≥0∧
|x[i]-q[i]|≥ρ2×|p[i]-q[i]|,
(5)
?i∈[1,d],(x[i]-q[i])(p[i]-q[i])>0∧
|x[i]-q[i]|>ρ2×|p[i]-q[i]|,
(6)
又由于ρ1<ρ2,因此
?i∈[1,d],(x[i]-q[i])(p[i]-q[i])≥0∧
|x[i]-q[i]|≥ρ1×|p[i]-q[i]|,
(7)
?i∈[1,d],(x[i]-q[i])(p[i]-q[i])>0∧
|x[i]-q[i]|>ρ1×|p[i]-q[i]|.
(8)
由(7)式和(8)式可得點xρ1-支配點p,與已知條件p是ρ1-支配輪廓點存在矛盾,所以數據點p一定是ρ2-支配輪廓點。
定理1的證明過程與數據流中ρ-支配輪廓查詢算法[20]的證明思路類似,但是結論正好相反。由定理1可以看出以“大于”作為關鍵的標準時,如果一點是較小ρ值的ρ-支配輪廓點,也必將是較大ρ值的ρ-支配輪廓點。
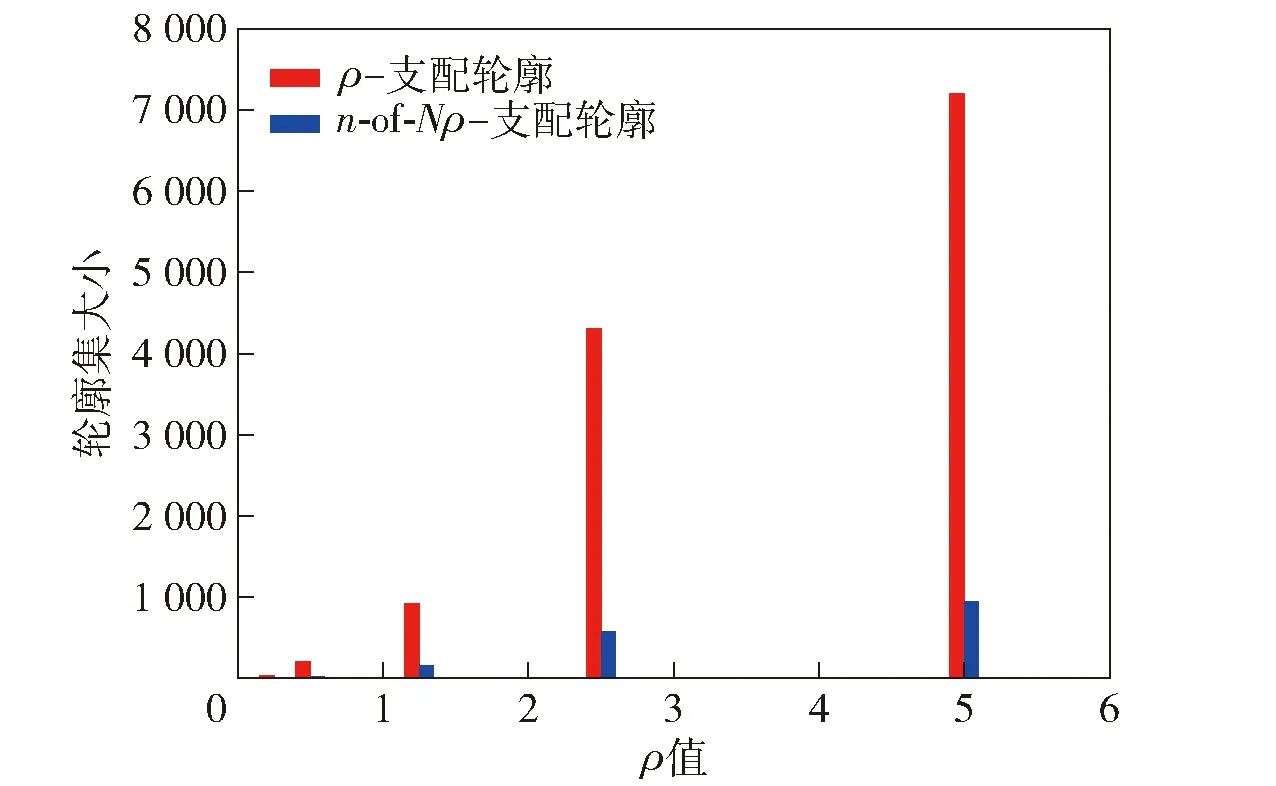
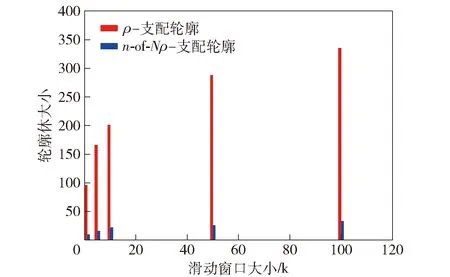
定理2給定數據流中的兩組多維數據點x和y,如果點yρ-支配點x并且L(x) 證明:由于點yρ-支配點x,所以當y屬于滑動窗口時點x不是ρ-支配輪廓點。又由于L(x) 定理3如果ρ≥1并且點xρ-支配點y以及點yρ-支配點z,則點xρ-支配點z. 證明:由點xρ-支配點y可得 ?i∈[1,d],(x[i]-q[i])(y[i]-q[i])≥0∧ (9) ?i∈[1,d],(x[i]-q[i])(y[i]-q[i])>0∧ (10) 由點yρ-支配點z可得 ?i∈[1,d],(y[i]-q[i])(z[i]-q[i])≥0∧ (11) ?i∈[1,d],(y[i]-q[i])(z[i]-q[i])>0∧ (12) 由(9)式乘以(11)式、(10)式乘以(12)式分別可得 ?i∈[1,d],(x[i]-q[i])(y[j]-q[i])2(z[i]- (13) ?i∈[1,d],(x[i]-q[i])(y[i]-q[i])2(z[i]- (14) 又由于(y[i]-q[i])2≥0并且ρ2>ρ,所以 ?i∈[1,d],(x[i]-q[i])(z[i]-q[i])≥0∧ (15) ?i∈[1,d],(x[i]-q[i])(z[i]-q[i])>0∧ (16) 由(15)式和(16)式可以得出點xρ-支配點y. 從定理3可以看出,以“大于”作為關鍵的標準,在ρ≥1時ρ-支配關系具有傳遞性,而在以“小于”作為關鍵的標準時不具有此性質。 定理4當ρ<1時,給定兩個點x和y并且x完全支配y,則xρ-支配y. 由于定理4的證明過程與定理1的證明過程類似,所以此處不再累述。 定理5如果ρ<1并且xρ-支配y以及y完全支配z,則xρ-支配z. 由于定理5與定理3的證明過程類似,所以此處不再累述。 當ρ≥1時,由定理3可知ρ-支配關系具有傳遞性,因此如果一點x被點yρ-支配,則被點xρ-支配的點一定被點yρ-支配。因此如果滑動窗口中的一個點x被后到達的另一個點yρ-支配,則點x不可能影響其他點是否為ρ-支配輪廓點。同時由定理2可得,如果滑動窗口中的一個點x被后到達的另一個點yρ-支配,則點x不可能成為ρ-支配輪廓點。綜上可以得出被后到達的點ρ-支配的點不可能成為ρ-支配輪廓點并且對其他點是否為ρ-支配輪廓點不產生影響。因此可以將滑動窗口中被后到達的點ρ-支配的點在ρ-支配輪廓計算之前過濾掉。用SN表示滑動窗口中過濾后點的集合,則SN中不包含被后到的點ρ-支配的點。由于要求計算出的結果是不被其他任意點ρ-支配的點的集合,因此可以將這些點分為一類,稱之為ρ-支配輪廓集合。SN中除了ρ-支配輪廓集合之外,還包含被先到達的點ρ-支配而不被后到達的點ρ-支配的點的集合,由于是被先到達的點ρ-支配,因此當ρ-支配它的點流出滑動窗口時,這些點有可能成為ρ-支配輪廓點,所以稱之為候選集合。綜上所述,在ρ≥1可以將SN分為兩類: 1)ρ-支配輪廓集合DN:SN中不被其他任何點ρ-支配的點的集合; 2) 候選集合CN:SN中不被后到達的點ρ-支配但是被先到達的點ρ-支配的點的集合。 從ρ≥1時的數據過濾方法和數據分類方法可以看出,ρ≥1時滑動窗口中數據過濾方式及集合劃分方式與以“小于”作為關鍵標準時不同,以“小于”作為關鍵標準時過濾掉的為被后到的點完全支配的點的集合,同時將滑動窗口中的數據分為了3類。 當ρ<1時,由定理2可知,如果滑動窗口中的一個點x被后到達的另一個點yρ-支配,則點x不可能成為ρ-支配輪廓點;然而,如果滑動窗口中的一個點x被后到達的另一個點yρ-支配,則點x不一定不影響其他的點是否為ρ-支配輪廓點,如圖4所示,圖中的數據點按照點a最先到達,b其次到達,c最后到達,并且ρ值取0.5,某個時刻點c剛剛到達滑動窗口且點a和點b沒有滑出滑動窗口。圖4中點a′與點q的距離為點a與點q距離的2倍,點b′與點q的距離為點b與點q距離的2倍。從圖4中可以看出:當ρ值為0.5時,點a的ρ-支配區域為點a′與點q形成的區域,點b的ρ-支配區域為點b′與點q形成的區域,由于數據點bρ-支配數據點a,所以數據點a不是ρ-支配輪廓點;按照ρ≥1時的數據過濾方法則將點a過濾掉,假如將數據點a過濾掉,由于點c不被點bρ-支配,因此點c為ρ-支配輪廓點。但是從圖4中可以看出點c被點aρ-支配,因此點c不是ρ-支配輪廓點,因此不能像ρ≥1時對滑動窗口中的數據進行過濾。 圖4 ρ<1時過濾錯誤示例Fig.4 Example of filtering error for ρ<1 由定理2、定理4、定理5可得,如果滑動窗口中的一個點x被后到達的另一個點y完全支配,則點x被點yρ-支配并且點x不可能影響其他的點是否為ρ-支配輪廓點。綜上可以得出被后到達的點完全支配的點不可能成為ρ-支配輪廓點并且對其他點是否為ρ-支配輪廓點不產生影響。因此可以將滑動窗口中被后到達的點完全支配的點在ρ-支配輪廓計算之前過濾掉,同樣用SN表示滑動窗口中過濾后點的集合。當ρ≥1時,將SN分成了DN和CN,DN為不被任何數據點ρ-支配的點的集合,CN為被先到的數據點ρ-支配但是不被后到的數據點ρ-支配的點的集合。但是當ρ<1時,由于過濾掉的是被后到的點完全支配的點的集合,因此除了以上兩類集合之外,SN中還有一些點是被后到的點ρ-支配而不被后到的點完全支配,這些點不可能成為ρ-支配輪廓點,因此將此類點稱之為輔助集合。綜上所述,當ρ<1時,可以將SN分為3類: 1)ρ-支配輪廓集合DN:SN中不被其他任何點ρ-支配的點的集合; 2) 候選集合CN:SN中不被后到的點ρ-支配但是被先到的點ρ-支配的點的集合; 3) 輔助集合AN:SN中不被后到的點完全支配但是被后到的點ρ-支配的點的集合。 從上述對數據流中ρ-支配輪廓查詢的數據過濾和數據分類方法可以看出,以“大于”作為關鍵標準當ρ<1時的數據過濾和分類方法與數據流中ρ-支配輪廓查詢算法[20]中當ρ≥1時的數據過濾和分類方法類似,而以“大于”作為關鍵標準當ρ≥1時無相關方法。 在此基礎上,本文對數據流中ρ-支配輪廓查詢算法進行了更改和擴展,算法1使用偽代碼描述了數據流中ρ-支配輪廓計算的過程(見表1)。當數據流中有新數據點p到達滑動窗口時:首先判斷滑動窗口是否已滿,如果是則先刪除滑動窗口中最先到達的數據,并且將被刪除的點ρ-支配的點從候選集移動到ρ-支配輪廓集;然后將點p插入到相應的空間區域中,在點p所屬的區域中查找出被點pρ-支配的集合DS,如果ρ≥1或者點p完全支配DS中的點則刪除,否則從ρ-支配輪廓集和候選集中移動到輔助集中;最后判斷是否有其他的點ρ-支配點p,如果有則將p加入到候選集,否則加入到ρ-支配輪廓集。 表1 算法1:數據流中ρ-支配輪廓查詢Tab.1 Algorithm 1:ρ-dominant skyline query in data stream 同3.1節所描述的一樣,用SN表示滑動窗口中進行數據過濾后的集合,由于當ρ≥1時ρ-支配關系和ρ-支配輪廓的性質與前面所述的性質沒有改變,所以被后到的點ρ-支配的點不可能成為ρ-支配輪廓點并且對其他點是否是ρ-支配輪廓點不產生影響,因此可以在n-of-Nρ-支配輪廓計算之前過濾掉,因此可得SN為不被后到的點ρ-支配的點的集合。在前面敘述中將不被其他點ρ-支配的點稱之為ρ-支配輪廓點,然而在n-of-Nρ-支配輪廓計算時,有些數據點雖然不被其他任意點ρ-支配,但由于位于滑動窗口的無效部分中,仍然不是ρ-支配輪廓點。通過n-of-Nρ-支配輪廓的定義可以得到n-of-Nρ-支配輪廓點只可能存在于滑動窗口的有效部分,因此將滑動窗口中有效部分不被其他任意點ρ-支配的點組成的集合稱之為n-of-Nρ-支配輪廓集。滑動窗口的有效部分除了n-of-Nρ-支配輪廓集之外,還包含被先到的點ρ-支配的點,由于這些點以后可能成為n-of-Nρ-支配輪廓點,因此將此部分點構成的集合稱之為候選集。由于滑動窗口中無效部分的數據點永遠不可能成為n-of-Nρ-支配輪廓點,但是可能影響其他點是否為n-of-Nρ-支配輪廓點,因此將無效部分沒有被過濾掉的點組成的集合稱之為輔助集。綜上所述,可以將SN分為3類: 1)n-of-Nρ-支配輪廓集合DN:SN中處于有效部分內并且不被其他任何點ρ-支配的點的集合; 2) 候選集合CN:SN中處于有效部分內并且不被滑動窗口中后到的點ρ-支配但是被先到的點ρ-支配的點的集合; 3) 輔助集合AN:SN中處于無效部分點的集合。 當ρ<1時,由于與ρ≥1時滿足不同的性質,所以當ρ<1時存在不同的數據過濾方式。同樣用SN表示滑動窗口中進行數據過濾后的集合,采用3.1節所述的同樣數據過濾方式,將滑動窗口中被后到達的點完全支配的點在n-of-Nρ-支配輪廓計算之前過濾掉,則可得SN為不被后到的點完全支配的點的集合。由于過濾掉的是被后到的點完全支配的點的集合,因此在滑動窗口的有效部分除了n-of-Nρ-支配輪廓集和候選集之外,還存在著被后到的點ρ-支配但是不被后到的點完全支配的點組成的集合。由于這部分點只是影響其他點是否為n-of-Nρ-支配輪廓點,并不可能成為n-of-Nρ-支配輪廓點,所以將這部分加入到輔助集合中。因此,滑動窗口中的數據點仍然可以分為3部分,只是3部分所包含的數據點與ρ≥1時有所不同。當ρ<1時,對SN的分類方法如下所示: 1)n-of-Nρ-支配輪廓集合DN:SN中處于有效部分內并且不被其他任何點ρ-支配的點的集合; 2) 候選集合CN:SN中處于有效部分內并且不被滑動窗口中后到的點ρ-支配但是被先到的點ρ-支配的點的集合; 3) 輔助集合AN:SN中處于無效部分的點和有效部分中被后到的點ρ-支配但是不被后到的點完全支配的點的集合。 在此基礎上,對數據流中n-of-Nρ-支配輪廓的計算過程給出了偽碼描述如算法2所示(見表2)。當數據流中有新數據點p到達滑動窗口時:首先判斷滑動窗口是否已滿,如果是則先刪除滑動窗口中最先到達的數據;然后將點p插入到相應的空間區域中;最后將n-of-Nρ-支配輪廓集返回給用戶。其中,滑動窗口中最先到達的數據刪除用DeletePoint( )函數來表示,新到達的數據插入用InsertPoint( )函數表示。由算法的描述可以看出算法2的時間復雜度依賴DeletePoint( )函數和InsertPoint( )函數的時間復雜度,由于兩個函數的時間復雜度均為O(N),所以算法2的時間復雜度為O(N)。 表2 算法2:數據流中n-of-Nρ-支配輪廓查詢Tab.2 Algorithm 2:n-of-Nρ-dominant skyline query in data stream 算法3描述了在數據流中計算n-of-Nρ-支配輪廓時將滑動窗口中最先到達的數據點p流出滑動窗口的過程(見表3)。第1行描述的是根據點p在數據流中的編號查找點p;第3行描述了計算要刪除點p所屬的空間區域的過程,在算法中用RegionCalculation( )函數[20]來表示,RegionCalculation( )函數包含兩個參數,第一個為所要計算的點p在各維上的數值部分value,第二個為查詢點q;第4~12行描述了對于點p所屬的每一個空間區域R的處理過程;第5行描述的為在空間區域R中刪除點p;第6~11行描述了對于空間區域R中的每一個點x,如果點p為點x的前ρ-支配點并且點x屬于候選集合(第7行),則將點x從候選集合移動到n-of-Nρ-支配輪廓集合中(第8~9行)。通過算法描述可以看出DeletePoint( )函數外層循環為區域個數R=2d,內層循環為滑動窗口中所屬R的數據N/2d,因此函數時間復雜度為O(N)。 表3 算法3:滑動窗口中數據刪除-DeletePoint( )Tab.3 Algorithm 3:data deletion in sliding window-DeletePoint( ) 算法4描述了在數據流中計算n-of-Nρ-支配輪廓時將新到達的點p插入到滑動窗口中的處理過程(見表4)。第1行通過調用RegionCalculation( )函數計算點p所屬的空間區域;第2~19行對于所屬的每一個區域進行處理,其中第3~17行為對滑動窗口中同一區域的其他數據進行處理,第18行描述的為將點p插入到所在空間區域中;第4~6行描述的為對于點p所屬區域中的一個點x,判斷其是否ρ-支配點p并且比已經ρ-支配點p的點編號大,如果是則更改點p的前ρ-支配點為x;第7~16行為討論點pρ-支配點x的情況,其中第8~10行描述的為如果點x屬于n-of-Nρ-支配輪廓集或者候選集并且位于滑動窗口的有效部分,則在其所屬的集合中將其移除;第11~12行為討論點x是否符合過濾的要求,如果符合,則將點x過濾掉;第13~15行描述的為點x不符合過濾的條件,如果位于滑動窗口的有效部分,則將點x轉換為輔助點;第20~23行描述了滑動窗口的有效部分中最先到達的一個點之前如果沒有被過濾掉,則從滑動窗口的有效部分轉移到無效部分;第24~28行描述的為如果點p在滑動窗口中不被先到的點ρ-支配,則將點p加入到n-of-Nρ-支配輪廓集,否則將其加入到候選集中。通過算法描述可以看出InsertPoint( )函數外層循環為區域個數R=2d,內層循環為滑動窗口中所屬R的數據N/2d,因此函數時間復雜度為O(N)。 表4 算法4:滑動窗口中新數據插入-InsertPoint( )Tab.4 Algorithm 4:new data insertion in slinding window-InsertPoint( ) 本節實驗中,系統地測試了ρ值、滑動窗口大小、維度對于計算時間和ρ-支配輪廓集大小的影響。由于每次滑動窗口內的數據統計可能存在差異,所以本節采用綜合滑動窗口滑動1 000次的情況,即統計ρ-支配輪廓集大小采用滑動窗口滑動1 000次過程中ρ-支配輪廓集大小的平均值,計算時間采用滑動窗口滑動1 000次過程中的計算時間總和。實驗中所要考察的主要參數及其變化范圍和默認值如表5所示,每次進行實驗只變化其中的一個參數,而其他參數設置為默認值。 表5 實驗參數變化范圍和默認值Tab.5 Changing range and default values of parameters 實驗數據為隨機生成的獨立分布數據,屬性包括裝甲車輛狀態的發動機水溫、發動機油壓、分動箱溫度、電流、儲氣瓶氣壓、水上液壓油溫、變速箱油溫及發動機轉速等,實驗時隨機選擇其中的兩維或者多維。數據自動生成時將數據限定在裝甲車輛的各屬性真實值域內,其中發動機水溫為-50~200 ℃,發動機油壓為0~1 000 kPa,分動箱溫度為0~150 ℃,電流為0~400 A,儲氣瓶氣壓為0~1.5 MPa,水上液壓油溫0~150 ℃,變速箱油溫為0~150 ℃,發動機轉速0~3 000 r/min. 部分隨機生成數據如表6所示。 表6 實驗數據示例Tab.6 Example of experimental data 本節使用C++語言實現了擴展的數據流中ρ-支配輪廓查詢算法和數據流中n-of-Nρ-支配輪廓查詢算法。實驗環境為Intel(R) Core(TM) i7-7700HQ CPU @2.80 GHz、8.00 G RAM內存和64位Win10操作系統。 4.2.1ρ值對算法的影響 本節測試了ρ值對于算法的影響。圖5顯示了ρ值對于輪廓集大小的影響,從中可以看出:隨著ρ值的增大輪廓集也變大,這是因為當ρ值增大時數據點所支配的面積變小,因此數據越難以被支配;但是無論ρ值如何變化,兩種算法的輪廓集都遠遠小于滑動窗口大小,因此應用于裝甲車輛狀態數據傳輸過程中所需傳輸的狀態數據量遠遠小于原數據量;而且n-of-Nρ-支配輪廓查詢算法的輪廓集遠遠小于ρ-支配輪廓算法的輪廓集,因此在裝甲車輛狀態傳輸過程中所需傳輸的數據量更小。圖6顯示了ρ值對于計算時間的影響,從中可以看出:當ρ<1時計算時間變化不大,當ρ>1時計算時間隨著ρ值的增大而增大,這是由于當ρ<1時過濾掉的為被后到的數據點完全支配的數據,因此過濾掉的數據相同;當ρ>1時過濾掉的數據為被后到的數據點ρ-支配的數據,隨著ρ增大,過濾掉的數據減少,因此計算時間變長;無論ρ值如何變化,兩種ρ-支配輪廓算法的計算時間相差不大。 圖5 ρ值對輪廓集大小的影響Fig.5 Effect of ρ on skyline size 圖6 ρ值對計算時間的影響Fig.6 Effect of ρ on computing time 4.2.2 滑動窗口大小對算法的影響 本節測試了滑動窗口大小對于算法的影響。圖7為滑動窗口大小對于輪廓集大小的影響,從中可以看出:隨著滑動窗口的增大輪廓集也變大;但是無論怎樣變化,輪廓集都遠遠小于滑動窗口的大小,因此在裝甲車輛狀態數據傳輸過程中應用ρ-支配輪廓查詢算法或者n-of-Nρ-支配輪廓查詢算法后所需傳輸的狀態數據量遠遠小于原數據量;而且n-of-Nρ-支配輪廓查詢算法的輪廓集遠遠小于ρ-支配輪廓算法的輪廓集,因此應用n-of-Nρ-支配輪廓查詢算法所需傳輸的狀態數據量更小。圖8為滑動窗口大小對于計算時間的影響,從中可以看出:隨著滑動窗口的增大計算時間也變大,這是由于隨著滑動窗口的增大,所需計算的數據量變大,因而導致計算時間增大,但是無論滑動窗口如何變化,兩種算法的計算時間基本一致。 圖7 滑動窗口對輪廓集大小的影響Fig.7 Effect of sliding window on skyline size 圖8 滑動窗口對計算時間的影響Fig.8 Effect of sliding window on computing time 4.2.3 維度對算法的影響 本節測試了裝甲車輛狀態數據的維度對于算法的影響。圖9顯示了輪廓集大小隨著數據維度的變化情況,從中可以看出:狀態數據的維度越大輪廓集越大,這是由于當維度增大時數據被支配的概率降低,從而使得數據成為輪廓點的概率增加,但是不管維度如何變化,輪廓集都遠遠小于滑動窗口大小,因此應用于裝甲車輛狀態數據傳輸過程中所需傳輸的狀態數據量遠遠小于原數據量;而且n-of-Nρ-支配輪廓查詢算法的輪廓集遠遠小于ρ-支配輪廓算法的輪廓集,因此在裝甲車輛狀態傳輸過程中所需傳輸的數據量更小。圖10顯示了計算時間隨著維度的變化情況,從中可以看出:計算時間隨著維度的變大而變大,這是由于當維度變大時,需要計算的數值增多,從而計算時間變大。 圖9 維度對輪廓集大小的影響Fig.9 Effect of dimension on skyline size 圖10 維度對計算時間的影響Fig.10 Effect of dimension on computing time 4.2.4 滑動窗口有效部分大小對算法的影響 最后,測試滑動窗口有效部分大小對于輪廓集大小的影響。圖11顯示了n-of-Nρ-支配輪廓集隨著滑動窗口有效部分增加而增大。這是由于只有位于滑動窗口中有效部分的數據點才可能成為n-of-Nρ-支配輪廓點,雖然整個滑動窗口的大小保持不變,但是滑動窗口中的有效部分所占的比例增大,所以滑動窗口中產生輪廓集的區間變大,因此相應的n-of-Nρ-支配輪廓集變大,進而通過調節滑動窗口有效部分的大小可以調整裝甲車輛狀態數據的傳輸量。 圖11 滑動窗口有效部分大小對輪廓集大小的影響Fig.11 Effect of effectiveness portion of sliding window on skyline size 在網絡時斷時續、網絡帶寬較小的網絡狀況受限情況下,采集的數據難以實時準確地傳輸到數據應用方,這嚴重制約著數據應用方利用數據對當前態勢進行評判。本文以裝甲車輛狀態數據傳輸應用為出發點,以“大于”作為關鍵的標準,重新對ρ-支配關系和ρ-支配輪廓進行討論,并對數據流中的ρ-支配輪廓查詢算法進行更改和擴展,用來滿足裝甲車輛狀態數據傳輸問題的需要;更進一步,對數據流中ρ-支配輪廓查詢算法進行擴展,提出了數據流中n-of-Nρ-支配輪廓查詢算法,進一步滿足網絡受限環境中裝甲車輛狀態關鍵數據選擇傳輸的要求;最后對算法進行了實驗,實驗表明改進的數據流中ρ-支配輪廓查詢算法以及數據流中n-of-Nρ-支配輪廓查詢算法能夠計算出數據流中的關鍵數據,對于網絡受限情況下裝甲車輛狀態數據傳輸起到重要的作用,并且數據流中n-of-Nρ-支配輪廓查詢相比于數據流中ρ-支配輪廓查詢具有更廣泛的應用,更適合應用于裝甲車輛狀態數據選擇傳輸過程中。 參考文獻(References) [1] TATBUL N,ETINTEMEL U,ZDONIK SB,et al.Load shedding in a data stream manager[C]∥Proceedings of the 29th International Conference on Very Large Data Bases.Berlin,Germany:VLDBEndowment,2003:309-320. [2] DE ASSUNCAO M D,VEITH A D S,BUYYA R.Distributed data stream processing and edge computing:asurvey on resource elasticity and future directions[J].Journal of Network &Computer Applications,2018,103:1-17. [3] BORZSONY S,KOSSMANN D,STOCKER K.The skyline operator [C]∥Proceedings of 17th International Conference on Data Engineering.Heidelberg,Germany:IEEE,2001:421-430. [4] PAPADIAS D,TAO Y F,FU G,et al.An optimal and progressive algorithm for skyline queries[C]∥Proceedings of the 2003 ACMSIGMOD International Conference on Management of Data.San Diego,CA,US:ACM,2003:467-478. [5] DING L L,XIN J C,WANG G R,et al.Efficient skyline query processing of massive data based on map-reduce[J].Chinese Journal of Computers,2011,34(10):1785-1796. [6] 余靖,劉盼盼.MapReduce框架下k-支配輪廓查詢算法[J].燕山大學學報,2014,38(6):532-537. YU J,LIU P P.k-dominant skyline query algorithm based on Map Reduce framework[J].Journal of Yanshan University,2014,38(6):532-537.(in Chinese) [7] LAI C C,AKBAR Z F,LIU C M,et al.Distributed continuous range-skyline query monitoring over the internet of mobile things[J].IEEE Internet of Things Journal,2019,6(4):6652-6667. [8] TIAN H,SIDDIQUE M A,MORIMOTO Y,et al.An efficient processing ofk-dominant skyline query in MapReduce[C]∥Proceedings of International Workshop on Bringing the Value of Big Data to Users.Hangzhou,China:ACM,2014:29-34. [9] ZHENG B,LEE K C,LEE W C.Location-dependent skyline query[C]∥Proceedings of International Conference on Mobile Data Management.Beijing,China:IEEE,2008:148-155. [10] LIU X,YANG D N,YE M,et al.U-Skyline:a new skyline query for uncertain databases[J].IEEE Transactions on Know-ledge and Data Engineering,2013,25(4):945-960. [11] REN W L,LIAN X,GHAZINOUR K.Skyline queries over incomplete data streams[J].The VLDB Journal,2019,28(6):961-985. [12] XIE M,WONG C W,LAL L A.An experimental survey of regret minimization query and variants:bridging the best worlds between top-k query and skyline query[J].The VLDB Journal,2020,29(1):147-175. [13] CHEN L,LIAN X.Dynamic skyline queries in metric spaces[C] ∥Proceedings of the 11th International Conference on Extending Database Technology:Advances in Database Technology.Nantes,France:ACM,2008:333-343. [14] 周劍剛,秦小麟,張珂珩,等.基于道路網的多移動用戶動態Skyline查詢[J].計算機科學,2019,46 (9):73-78. ZHOU J G,QIN X L,ZHANF K H,et al.Dynamic skyline query for multiple mobile users based on road network[J].Computer Science,2019,46 (9):73-78.(in Chinese) [15] ZOU L,CHEN L,?ZSU M T,et al.Dynamic skyline queries in large graphs[C]∥Proceedings of International Conference on Database Systems for Advanced Applications.Tsukuba,Japan:Springer,2010:62-78. [16] LI H,YOO J.An efficient scheme for continuous skyline query processing over dynamic data set[C]∥Proceedings of 2014 International Conference on Big Data and Smart Computing.Bangkok,Thailand:IEEE,2014:1197-1206. [17] 張麗,鄒鵬,賈焰,等.數據流上連續動態skyline查詢研究[J].計算機研究與發展,2015,48(1):77-85. ZHANG L,ZOU P,JIA Y,et al.Continuous dynamic skyline queries over data stream[J].Journal of Computer Research and Development,2015,48(1):77-85.(in Chinese) [18] BAI M,XIN J C,WANG G R,et al.Research on dynamic skyline query processing over data streams[J].Chinese Journal of Computers,2011,34(10):1876-1884. [19] 信俊昌,白梅,東韓,等.一種ρ-支配輪廓查詢的高效處理算法[J].計算機學報,2011,34(10):1876-1884. XIN J C,BAI M,DONG H,et al.An efficient processing algorithm forρ-dominant skyline query[J].Chinese Journal of Computers,2011,34(10):1876-1884.(in Chinese) [20] 王之瓊,霸建民,黃達,等.數據流中ρ-支配輪廓查詢算法[J].計算機科學與探索,2017,11(7):1080-1091. WANG Z Q,BA J M,HUANG D,et al.ρ-dominant skyline computation on data streams[J].Journal of Frontiers of Computer Science and Technology,2017,11(7):1080-1091.(in Chinese)
|x[i]-q[i]|≥ρ×|y[i]-q[i]|,
|x[i]-q[i]|>ρ×|y[i]-q[i]|.
|y[i]-q[i]|≥ρ×|z[i]-q[i]|,
|y[i]-q[i]|>ρ×|z[i]-q[i]|.
q[i])≥0∧|x[i]-q[i]|≥ρ2×|z[i]-q[i]|,
q[i])>0∧|x[i]-q[i]|>ρ2×|z[i]-q[i]|.
|x[i]-q[i]|≥ρ×|z[i]-q[i]|,
|x[i]-q[i]|>ρ×|z[i]-q[i]|.3 數據流中ρ-支配輪廓和n-of-Nρ-支配輪廓
3.1 數據流中ρ-支配輪廓查詢


3.2 數據流中n-of-Nρ-支配輪廓查詢



4 實驗說明和實驗方案
4.1 實驗說明

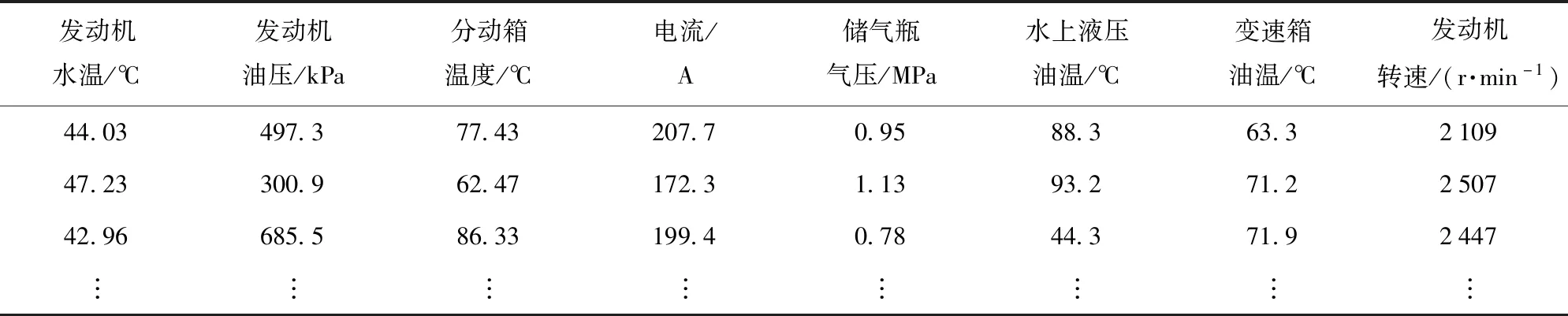
4.2 實驗方案





5 結論

