基于樸素貝葉斯的機器學習實驗教學設計

王敏 羅婧雯 劉軍 劉沛澤

【摘要】? ? 貝葉斯學習是機器學習理論中的重要研究方向。本文主要實現基于樸素貝葉斯的機器學習實驗教學設計，貝葉斯學習以貝葉斯法則為基礎，通過已了解的數據分布的先驗知識，結合樣本訓練數據來估算出整體數據的數學模型。貝葉斯學習的結果是獲得一組變量的聯合概率分布。貝葉斯學習由于其用概率的形式來表示不確定知識，故對不確定形式的問題它有獨特的描述和計算優勢。而樸素貝葉斯是在屬性獨立性假設的條件下進行計算，可以大大減小計算的復雜程度。實驗設計目的是根據樸素貝葉斯公式實現對文檔的分類，給學生提供一種實驗教學案例。

【關鍵詞】? ? 樸素貝葉斯? ? 實驗教學設計? ? 文本分類

一、實驗研究背景與目的

本實驗設計主要基于樸素貝葉斯理論，目前是為學生提供基于貝葉斯理論的實驗項目，讓學生更好地理解該理論解決實際問題。 隨著互聯網的飛速發展， 海量數據注入到通訊設備中。如此大量的信息就讓信息檢索和數據挖掘的重要性更加突出。文本分類作為數據挖掘的一部分也逐漸被人們重視起來。其中文本分類的主要內容是在預先給定的類標簽的集下， 根據文章內容， 確定它的類別。我們接下來將要通過三個方面來介紹：文本表示， 分類器構造和分類器評估。

二、實驗設計思路

本實驗的思路是把一部分含有女性、體育、文學出版、校園的話題用網絡爬蟲爬下來存在特定的文檔中，然后通過樸素貝葉斯分類算法實現貝葉斯分類。

三、方案設計

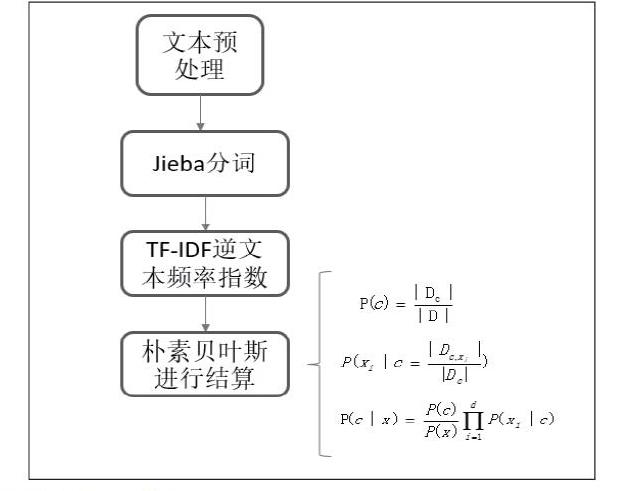
系統設計流程框圖如下。

四、具體算法描述

除去噪聲，如格式轉換，去掉符號，整體規范化;遍歷的讀取一個文件下的每個文本。操作如下。

def readFile（path）：

with open（path， 'r'， errors='ignore'） as file：

content = file.read（）

return content

def saveFile（path， result）：

with open（path， 'w'， errors='ignore'） as file：

file.write（result）

4.1 jieba分詞

1）首先利用import調用jieba模塊、TF-IDF分詞模塊、樸素貝葉斯算法模塊;

import jieba

2）jieba分詞算法的基本原理是：1.基于前綴詞典實現高效的詞圖掃描，生成句子中漢字所有可能成詞情況所構成的有向無環圖（DAG）; 2.采用動態規劃查找最大概率路徑，找出基于詞頻的最大切分組合; 3.對于未登錄詞，采用了基于漢字成詞能力的HMM模型，使用了Viterbi算法;

代碼如下：

def segText（inputPath， resultPath）：

fatherLists = os.listdir（inputPath）

for eachDir in fatherLists：

eachPath = inputPath + eachDir + "/"? ? ? ? ? each_resultPath = resultPath + eachDir + "/"

if not os.path.exists（each_resultPath）：

os.makedirs（each_resultPath）

childLists = os.listdir（eachPath）

for eachFile in childLists：

eachPathFile = eachPath + eachFile

#? print（eachFile）

content = readFile（eachPathFile）

# content = str（content）

result = （str（content））.replace（"＼r＼n"， ""）.strip（）

# result = content.replace（"＼r＼n"，""）.strip（）

cutResult = jieba.cut（result）

saveFile（each_resultPath + eachFile， " ".join（cutResult））

4.2 TF-IDF逆文本頻率指數

1）首先調用TF-IDF向量轉換類和向量生成類。

from sklearn.feature_extraction.text import TfidfTransformer

from sklearn.feature_extraction.text import TfidfVectorizer

2）TF-IDF逆文本頻率指數是一種用于信息檢索與數據挖掘的常用加權技術。是一種統計方法，用以評估一個詞對于一個語料庫中一份文件的重要程度。詞的重要性隨著在文件中出現的次數正比增加，同時隨著它在語料庫其他文件中出現的頻率反比下降。

3）TF-IDF詞頻算法實現。一個詞在某一文檔中出現次數比較多，其他文檔沒有出現，說明該詞對該文檔分類很重要。然而如果其他文檔也出現比較多，說明該詞的區分性不大，就用IDF來降低該詞的權重。

TF-IDF=TF×IDF

其中，詞頻：TF=詞在文檔中出現的次數/文檔中總詞數;

逆文本頻率：IDF=log（語料庫中文檔總數/包含該詞的文檔數+1）。

def getTFIDFMat（inputPath， stopWordList， outputPath）：

bunch = readBunch（inputPath）

tfidfspace = Bunch（target_name=bunch.target_name，label=bunch.label， filenames=bunch.filenames， tdm=[]，

vocabulary={}）

vectorizer = TfidfVectorizer（stop_words=stopWordList， sublinear_tf=True， max_df=0.5）

transformer = TfidfTransformer（）

tfidfspace.tdm = vectorizer.fit_transform（bunch.contents）

tfidfspace.vocabulary = vectorizer.vocabulary_

writeBunch（outputPath， tfidfspace）

4.3樸素貝葉斯分類法

1）首先調用貝葉斯分類法算法模塊，這個模塊是調用已有的別人寫好的算法，下面會詳細介紹原理過程。

from sklearn.naive_bayes import MultinomialNB

2）樸素貝葉斯原理

樸素貝葉斯分類器采用了“屬性條件獨立性假設” 對已知類別假設所有屬性相互獨立。換言之，假設每個屬性獨立地對分類結果發生影響。故貝葉斯公式可以重寫為

因為給定樣本P（x）為已知的，故貝葉斯準則就可以轉化為

顯然，樸素貝葉斯分類器的訓練過程就是基于訓練集 D 來估計類先驗概率P（c），并為每個屬性估計條件概率。

令Dc表示訓練集D中第c類樣本組成的集合，若有充足的獨立同分布樣本則可容易地估計出類先驗概率。

對離散屬性而言，令表示Dc中在第i個屬性上取值為的樣本組成的集合，則條件概率可估計為

程序如下：

def bayesAlgorithm（trainPath， testPath）：

trainSet = readBunch（trainPath）

testSet = readBunch（testPath）

clf = MultinomialNB（alpha=0.001）.fit（trainSet.tdm， trainSet.label）

#alpha：0.001 alpha 越小，迭代次數越多，精度越高

#print（shape（trainSet.tdm））? #輸出單詞矩陣的類型

#print（shape（testSet.tdm））

predicted = clf.predict（testSet.tdm）

total = len（predicted）

rate = 0

for flabel， fileName， expct_cate in zip（testSet.label， testSet.filenames， predicted）：

if flabel ！= expct_cate：

rate += 1

print（fileName， "：實際類別："， flabel， "-->預測類別："， expct_cate）

print（"erroe rate："， float（rate） * 100 / float（total）， "%"）

五、系統測試情況

下圖中data文件夾中是原始數據，result文件夾是jieba分詞結果，stop是文本預處理篩掉的的停用詞。test是測試數據，test_segResult是測試結果。

其中測試數據集：女性話題有38個，體育話題115個，文學出版話題31個，校園話題16個，以下是測試出錯的結果。其中校園話題出錯的概率最大。

六、小結

此程序簡單易懂，是在貝葉斯的基礎上進一步了解了樸素貝葉斯公式的原理及其運用，介紹了jieba分詞和TF-IDF逆文本頻率指數及其應用，在實際案例中錯誤率僅為0.570，準確率較高，可以在實驗課程教學中使用。

參? 考? 文? 獻

[1]蘇金樹， 張博鋒， 徐昕.基于機器學習的文本分類技術研究進展[J].軟件學報， 2006， 17 （09） ：1848-1859.

[2]李學明， 李海瑞， 薛亮， 何光軍.基于信息增益與信息熵的TFIDF算法[J].計算機工程， 2012， 38 （08） ：37-40.

[3]Tom M.Mitchell著;曾華軍等譯，機器學習[M]. 機械工業出版社，2003.

[4]陳葉旺，余金山. 一種改進的樸素貝葉斯文本分類方法[J].? 華僑大學學報（自然科學版）. 2011（04）.