以問題引導自主探究促進深度學習

楊梅芳

摘要：本文以《一次函數的圖像（1）》教學設計為例，闡述問題在誘發學生思維、促進學生深度學習中的積極性作用，并提出創設問題時，要注意規劃復習問題，精準切入，揭示新知生長點;創設情境問題，步步追問，引導自主探究;布局展延問題，層層遞進，實現深度思維;設好小結問題，提煉整理，誘發繼續探索的相關問題，供有關教師參考。

關鍵詞：問題;生長點;自主探究;深度思維

中圖分類號：G633.6 文獻標識碼：A文章編號：1992-7711（2021）07-091

數學教學是培養學生思維的教學，而培養學生的思維要依靠課堂上由問題產生的問題的引導，一個個懸念吸引著學生，思維的火花能時時迸發，課堂效率也就能大大提高。因此，要讓課堂充滿思維、充滿智慧、充滿探求，必須設置一系列能激起思維、引發探求欲的精彩問題，以此促進學生的真學習、深度學習。

一、教學案例

以《一次函數的圖像（1）》教學設計為例，闡述問題在誘發學生思維、促進學生深度學習中的積極性作用。

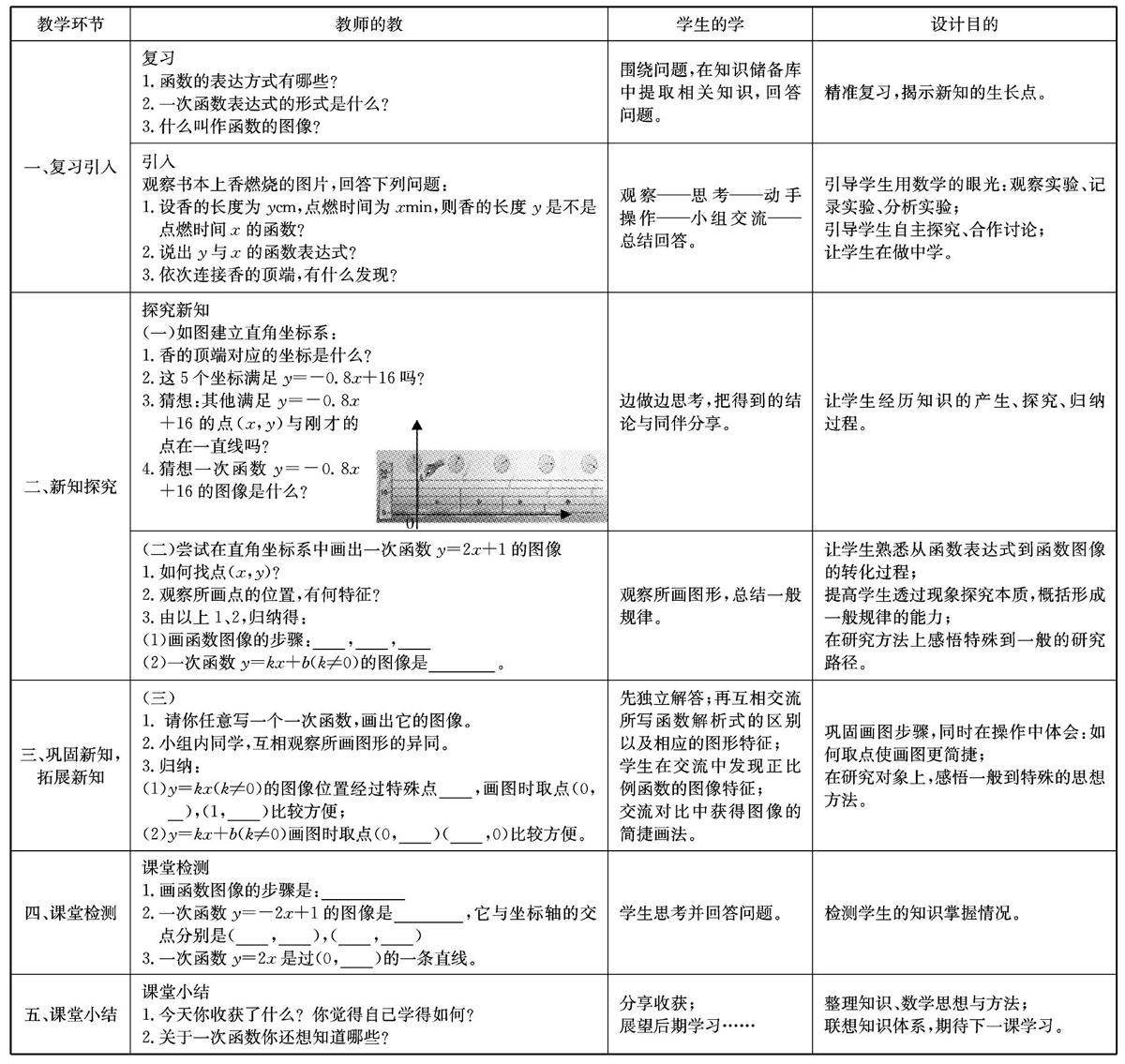
教學環節教師的教學生的學設計目的

一、復習引入

復習

1.函數的表達方式有哪些？

2.一次函數表達式的形式是什么？

3.什么叫作函數的圖像？圍繞問題，在知識儲備庫中提取相關知識，回答問題。精準復習，揭示新知的生長點。

引入

觀察書本上香燃燒的圖片，回答下列問題：

1.設香的長度為ycm，點燃時間為xmin，則香的長度y是不是點燃時間x的函數？

2.說出y與x的函數表達式？

3.依次連接香的頂端，有什么發現？觀察——思考——動手操作——小組交流——總結回答。引導學生用數學的眼光：觀察實驗、記錄實驗、分析實驗;

引導學生自主探究、合作討論;

讓學生在做中學。

二、新知探究

探究新知

（一）如圖建立直角坐標系：

1.香的頂端對應的坐標是什么？

2.這5個坐標滿足y=-0.8x+16嗎？

3.猜想：其他滿足y=-0.8x+16的點（x，y）與剛才的點在一直線嗎？

4.猜想一次函數y=-0.8x+16的圖像是什么？

邊做邊思考，把得到的結論與同伴分享。讓學生經歷知識的產生、探究、歸納過程。

（二）嘗試在直角坐標系中畫出一次函數y=2x+1的圖像

1.如何找點（x，y）？

2.觀察所畫點的位置，有何特征？

3.由以上1、2，歸納得：

（1）畫函數圖像的步驟：

，? ，

（2）一次函數y=kx+b（k≠0）的圖像是_____________。 觀察所畫圖形，總結一般規律。讓學生熟悉從函數表達式到函數圖像的轉化過程;

提高學生透過現象探究本質，概括形成一般規律的能力;

在研究方法上感悟特殊到一般的研究路徑。

三、鞏固新知，

拓展新知（三）

1. 請你任意寫一個一次函數，畫出它的圖像。

2.小組內同學，互相觀察所畫圖形的異同。

3.歸納：

（1）y=kx（k≠0）的圖像位置經過特殊點? ，畫圖時取點（0， ），（1，? ）比較方便;

（2）y=kx+b（k≠0）畫圖時取點（0，? ）（? ，0）比較方便。先獨立解答;再互相交流所寫函數解析式的區別以及相應的圖形特征;

學生在交流中發現正比例函數的圖像特征;

交流對比中獲得圖像的簡捷畫法。鞏固畫圖步驟，同時在操作中體會：如何取點使畫圖更簡捷;

在研究對象上，感悟一般到特殊的思想方法。

四、課堂檢測課堂檢測

1.畫函數圖像的步驟是：

2.一次函數y=-2x+1的圖像是_____________，它與坐標軸的交點分別是（? ，? ），（? ，? ）

3.一次函數y=2x是過（0，? ）的一條直線。學生思考并回答問題。檢測學生的知識掌握情況。

五、課堂小結課堂小結

1.今天你收獲了什么？你覺得自己學得如何？

2.關于一次函數你還想知道哪些？分享收獲;

展望后期學習……整理知識、數學思想與方法;

聯想知識體系，期待下一課學習。

二、教學反思

創設問題，就是把知識的產生、發展、應用過程以問題的形式提出來，讓學生去思考。目的鮮明地設問，可以使啟發性更強，探究過程更高效。

1.規劃復習問題，精準切入，揭示新知生長點。

復習問題要精準規劃，不是簡單的以上節課所學作為本節課復習的內容，而是要找準學習生長點，由舊知伸向新知。如此，可以使學生復習的指向更明確，為新課做好充分的知識準備，同時抓住數學知識的前后聯系，精準切入，體現知識的邏輯順序，揭示數學的內部關聯。

需要注意的是，這個環節的設問一要精煉，不能用時過長;二要精準，抓住切入新知的時機，以有效引發學生探究新知的內驅力。

2.創設情境問題，步步追問，引導自主探究。

課的開始階段，創設情境問題能集中學生注意力，吸引學生快速進入學習狀態，一個貼近生活、貼近實際、學生熟悉的問題，更能誘發學生主動觀察、聯想，進而在問題的指引下，進入抽象、概括、數學化的過程。這樣學生新知探究之路便成功開啟，學生想學、樂學、主動學得積極情態得以激發。

需要注意的是，情境問題的設置一要重視利用教材提供的素材，二要研究圖文內容編寫的背景和意圖，深入挖掘其教學價值，讓學生在學習中體會數學的價值。

3.布局展延問題，層層遞進，實現深度思維。

新知的展延階段一般是課的重點和難點。設問時要根據具體內容，精心布局、層層推進，為學生的深入探究鋪好臺階，發揮“GPS”的作用。

需要注意的是，這個環節中問題的解決，老師要放手。別林斯基說：“教學方法應該使學生自覺地掌握知識，使他們發展積極的思維”。讓學生自己去尋求問題的正確解答，這種內需的力量有助于他們領會知識和掌握技巧，當他們嘗到成功的樂趣后，對學習的熱愛就是很自然的事了，而且持續的、積極的求知欲對他們一生的發展都具有重大意義。

4.設好小結問題，提煉整理，誘發繼續探索。

課堂小結時，要改變以教師為主體陳述的總結方式。以上課例中我請同學們思考了兩個問題。一是“今天你收獲了什么？你覺得自己學得如何？”我鼓勵學生采用多種形式的自主小結和自主評價：或小組討論代表發言，或個人上臺發言其他學生補充，最后是老師補充完善，及時評價、鼓勵。二是“關于一次函數你還想知道哪些？”此問旨在引導學生基于本課的內容進行合理聯想，為下一節的教學內容做好鋪墊;同時通過類比同類知識的學習，以期獲得相關的學習經驗和方法;尤為重要的是延續學生飽滿的學習熱情、積極的思維狀態。

需要注意的是，小結問題的解答主要以表述為主，體現學生的語言表達和概括能力，學生的回答不一定全面，所以課堂小結環節要留有一定的時間，讓學生互相補充，在知識和思想方法兩個層面充分總結，并對知識的延伸做好伏筆。

課堂中一串由淺入深、由表及里、由簡到繁的有梯度的探索性問題，是學生目標達成的腳手架，能讓課堂充滿靈動、充滿思維。學生在探求問題的過程中，學習的積極性得以調動，學習的動機水平得以提高，成功的機會得以創造，良好的意志品質得以培養，學習興趣得以激發，學生也就始終處在深度學習之中。

（作者單位：無錫市后宅中學，江蘇 無錫214145）