考慮脈動風下弓網離線影響的高速鐵路接觸網可靠性分析*

朱鵬宇，萬后林，張 鵬

(1.淮陰工學院 建筑工程學院，江蘇 淮安 223000；2.江蘇東辰建材有限公司，江蘇 淮安 223000)

0 引言

高速鐵路牽引供電系統中，因接觸網設備長期戶外運行，易受自然環境影響。至2020年底，我國鐵路運行里程達14.6萬km，其中高鐵約占20%[1]。列車高速運行對弓網間良好受流要求較高，弓網間良好受流決定供電質量好壞及行車可靠性[2]。國內外學者針對接觸網抗風穩定性做大量研究，但僅停留在通過建立受電弓、接觸網模型研究兩者間相互作用，關于風與弓網2者干擾問題研究較少[3-5]。文獻[6]表明接觸網系統受脈動風影響形成抖振，增加弓網間離線率。弓網離線使受流不連續影響列車平穩運行，離線電弧產生高溫，降低接觸線使用壽命以及供電穩定裕量。目前，針對接觸網結構研究，忽略自然環境尤其是西北地區脈動風對接觸網系統可靠性影響。

因此，本文通過諧波疊加法模擬西北地區脈動風風速時程，對風速區間分布概率進行統計，將脈動風下弓網接觸壓力及弓網離線率作為衡量接觸網系統可靠性新指標，利用接觸網系統GO-FLOW模型對脈動風下接觸網可靠性進行分析。

1 脈動風場模擬

自然風具有隨機性與不確定性，在順向時程曲線中，將自然風分為平均風和脈動風：平均風頻率低，對接觸線產生作用力為靜力[7]；脈動風強度隨機更替，周期短，對接觸線作用力引起弓網振動。因此，本文主要集中于脈動風研究。

在三維空間內，某處自然風速如式(1)所示：

(1)

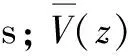
時域法需通過現場實測、風洞試驗等獲取風速時程樣本，過程比較繁瑣。因此，本文采用數值模擬法模擬風速時程。

1.1 脈動風場數值模擬方法

常用脈動風速時程仿真手段包括[8]線性自回歸濾波(AR)法、諧波積累(WAWS)法、隨機傅里葉特征法及小波重構法。其中，WAWS法具有適用范圍廣、模擬精度高等優點，適用于接觸網脈動風場模擬。脈動風概率符合高斯分布，將脈動風變換為一維零均值平穩高斯隨機過程向量，如式(2)所示：

v(t)={v1(t),v2(t),…,vM(t)}T

(2)

則互譜分布函數矩陣如式(3)所示：

(3)

對式(3)進行Cholesky分解，結果如式(4)～(5)所示：

S(ω)=G(ω)·G*T(ω)

(4)

(5)

空間中任意點x時程曲線如式(6)所示：

(6)

式中：Δω=ωup/N為頻率增量；ωup=ωmax-ωmin為截止頻率；i=1,2,3,…,n；N為數值足夠大的正整數；Gim為G(ω)中元素；θim為|Gim(ωml)|幅角，(°)；ωml為雙索引頻率。

1.2 脈動風速功率譜函數選取

本文將Davenport譜作為脈動風速功率譜函數[8]，如式(7)所示：

(7)

式中：f為脈動風頻率；S(f)為Davenport譜函數；k為風區所在地的地面粗糙度系數；v10為標準高度為10 m某點平均風速，m/s。

在空間中，任意兩點間互功率譜如式(8)所示：

(8)

式中：Saa(ω)、Sbb(ω)分別表示a、b自功率譜函數；coh(Δab,ω)為a、b相關性函數；ω為角頻率；Cx表示空間任意兩點相關性在x方向衰減程度系數；U(z)為導高處平均風速，m/s；φ(ω)為風速相位角。其中，φ(ω)如式(9)所示：

(9)

式中：Δx=|xa-xb|表示a、b在x方向距離。

將風區參數數據代入式(7)～(9)得到自功率譜及該風區互功率譜系數，構成互功率譜函數矩陣；對互功率譜函數作Cholesky分解，將結果匯總代入式(6)，通過MATLAB仿真模擬得到風速時程曲線。

2 接觸網脈動風場仿真

2.1 接觸網脈動風風速時程仿真

基于MATLAB平臺，采用脈動風速功率譜函數對西北某風區單點脈動風速進行仿真[9-10]。WAWS法模擬脈動風仿真參數見表1。

表1 WAWS法模擬脈動風仿真參數

脈動風風速時程曲線如圖1所示。由圖1可知，脈動風分布于-30～30 m/s，正負號代表脈動風風向。

圖1 脈動風風速時程曲線

2.2 脈動風風速概率分布

脈動風風速時程曲線符合高斯分布，由圖1可知，高斯分布參數μ=0.563 9，σ2=9.603。利用MATLAB繪制脈動風速概率分布如圖2所示。

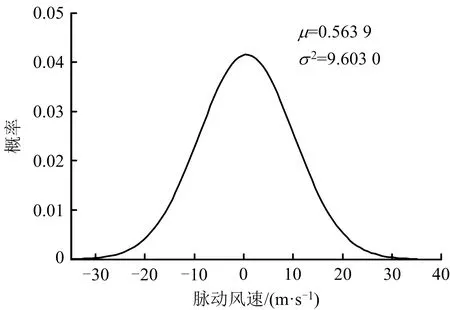
圖2 脈動風風速概率分布

利用Normspec函數計算得到脈動風風速概率，脈動風風速概率分布統計見表2(正負號代表風速方向)。

表2 脈動風風速概率分布統計

3 脈動風下弓網離線特性

3.1 脈動風對弓網受流影響

接觸網系統在脈動風作用下發生抖振，影響行車可靠性。通過對某段鐵路弓網接觸壓力進行動態仿真，得到不同風速下接觸壓力，見表3。

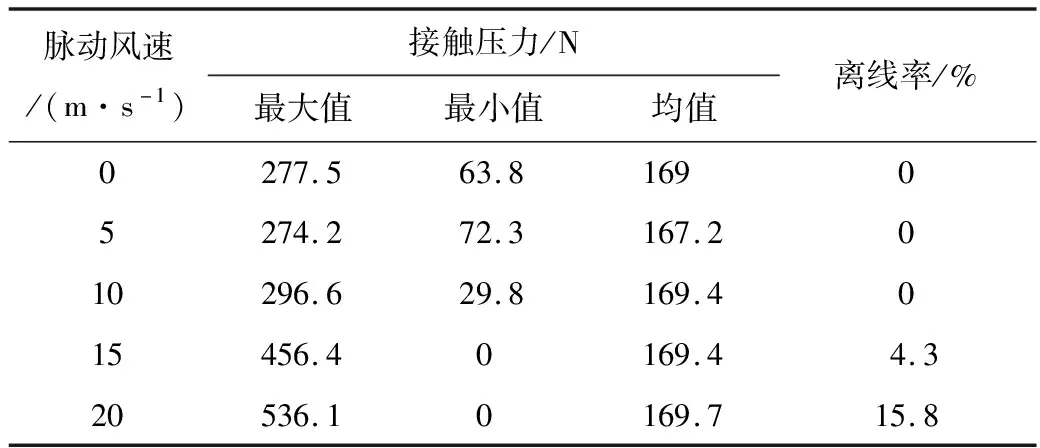
表3 不同風速下接觸壓力

由表3可知，當脈動風速大于10 m/s時，弓網間接觸壓力明顯增大；當風速為20 m/s時，接觸壓力差值為536.1 N，離線率15.8%，將影響行車安全。

3.2 脈動風下弓網離線故障率

不同脈動風速下離線率不同。分別計算不同脈動風速下弓網離線率，見表4。

表4 脈動風下弓網離線率

4 脈動風下接觸網系統可靠性分析

傳統接觸網系統可靠性研究沒有將西北地區大風運行環境因素考慮在內，導致可靠性計算結果與實際偏差較大。因此，本文將脈動風下弓網離線故障率納入接觸網系統可靠性分析指標，并對其可靠性進行分析。

4.1 高速鐵路接觸網系統可靠性模型建立

接觸網系統主要由6部分串聯組成：接觸懸掛裝置、定位裝置、支持裝置、附屬懸掛、補償裝置以及支柱與基礎裝置等[11]。

本文采用GO-FLOW法進行接觸網系統可靠性分析[12]。GO-FLOW法由日本學者在GO法基礎上提出，是1種新的可靠性分析方法[13-14]。

首先根據接觸網系統結構，以接觸網能夠正常運行為導向，建立計及脈動風下弓網離線因素接觸網系統GO-FLOW圖，如圖3所示。其中A、B、C、D、E、F分別表示接觸網6個組成部分，M表示脈動風下弓網離線因素，箭頭信號流代表接觸網系統可靠度。操作符25、21、35分別表示信號制造單元、接觸網6個組成部件以及隨時間發生失效的工作單元。假定P、Po分別表示操作符本身固有故障率及輸出故障率；R、Ro為操作符固有穩定性及相應傳遞穩定性；Pi、Ri為輸入操作符信號故障率及可靠度。則每個操作信號計算邏輯：

圖3 計及脈動風下弓網離線的接觸網系統GO-FLOW圖

1)25號操作符即信號制造單元，其輸出可靠性大小和故障可能性，如式(10)～(11)所示：

R=Ro

(10)

P=Po

(11)

2)21號操作符代表2個狀態單元，其輸出信號和故障率如式(12)～(13)所示：

Ro=Ri+R

(12)

Po=Pi+P

(13)

3)35號操作符代表隨時間失效的工作單元，若失效單元故障率為常數K，則其輸出可靠度與故障率如式(14)～(15)所示：

Ro=Rie-Kt

(14)

Po=Pie-Kt

(15)

式中：t為持續時間，s；e為常數。

4.2 接觸網系統可靠度計算

接觸網系統GO-FLOW圖共包括21個操作符，根據文獻[15]得到接觸網系統各組成單元操作符可靠性參數，見表5。

表5 接觸網系統各組成單元操作符可能性參數

利用GO-FLOW計算規則得到接觸網系統GO-FLOW圖對應信號流強度，見表6。

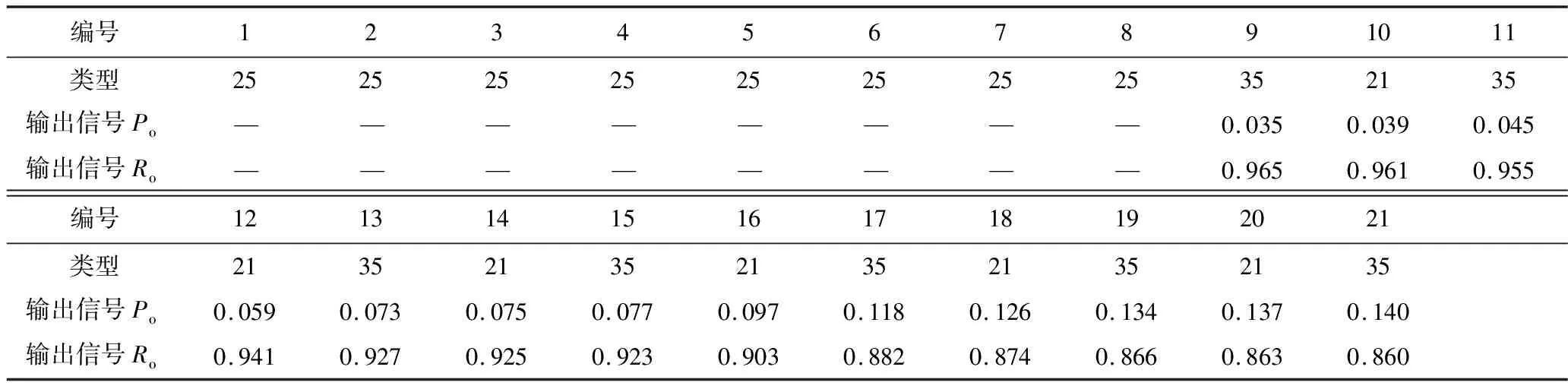
表6 接觸網系統GO-FLOW圖中信號流強度

4.3 接觸網可靠度對比分析

對比考慮脈動風前后接觸網可靠度計算結果，如圖4所示。由圖4可知，當未考慮脈動風因素時，接觸網系統最終可靠度R=0.896；考慮脈動風時接觸網系統最終可靠度R=0.860，相差3.6%，且脈動風下弓網離線故障率為0.026，與接觸網系統某些部件故障率相當。因此，對大風區接觸網系統可靠性分析時，必須考慮脈動風對弓網離線影響。

圖4 考慮脈動風前后接觸網系統可靠度對比

通過對西北地區接觸網故障數據統計可知，初步設計階段可以通過增加防舞鞭、防風墻等增強腕臂結構和接觸線強度，降低脈動風影響作用。

5 結論

1)脈動風風速在10～35 m/s分布概率高達29.82%，需有針對性采取防風措施，例如增設防舞鞭等。

2)考慮脈動風下弓網離線影響，接觸網系統可靠度略有下降，且故障率高達0.026，與接觸網系統組成部件故障率相當，嚴重影響列車運行安全。

3)為滿足高速行車需求，保障列車安全運行，需從多方面著手解決西北風區脈動風影響，例如改進接觸網配件性能、定期對接觸網系統進行檢修維護以及對接觸網關鍵設備服役狀態進行監測與預警。