基于教學目標達成度分析的《復變函數》課程的教學探索
張克磊 林昕茜 唐生強
(桂林電子科技大學數學與計算科學學院 廣西·桂林 541004)
復變函數是高等學校工科類本科的一門重要的基礎課,其理論和方法在微分方程、積分方程、流體力學、電學、熱學等方面有著重要的應用。復變函數是實變函數的思想、理論和方法在復數域上的推廣和發展,兩者在內容上既有一致的地方,又有很大的區別。復變函數是我校信息對抗技術、自動化類、電子信息類等專業的基礎必修課程,通過本課程的學習,為學生學習后繼專業課程和解決某些實際問題提供必要的理論和方法,進一步培養學生的抽象思維能力、自主學習能力以及綜合運用知識解決實際問題的能力。很多高校對復變函數課程進行了一些教學改革和實踐。由于復變函數課程在教學實踐中具有知識點多、難點多、課時少等的特點,導致此課程的教學效果不理想,掛科率高等問題。我校處于西部地區,面對教學資源相對薄弱和學生水平相對較低的教學狀況,基于教學目標達成度分析和成果導向理念,本文對《復變函數》課程進行了一些教學方法的改革和實踐。
1 《復變函數》課程教學目標達成度
根據我校電子信息類專業、信息對抗專業等的畢業條件和成果導向理念,制定了如下2個課程目標:課程目標1是通過學習本課程,使學生掌握復變函數的基本理論和方法,能熟練地應用所學知識分析、解決專業課程中的實際問題。課程目標2是通過本課程的學習,培養學生的邏輯推理能力、抽象思維能力、空間想象能力、辯證思維能力以及綜合運用知識解決工程中的實際問題的能力。通過比較實變函數與復變函數的異同,理解對立統一的辯證規律,培養學生的辯證思維能力,勇于探索的科學精神,幫助學生樹立科學的價值觀和責任感。課程目標1和課程目標2都是支撐畢業條件中的指標點1-1,即掌握工科類專業必需的數學知識、數學方法和數學思維。
本文以我校2020—2021學年第1學期的《復變函數》課程其中一個班級期末考試試題為例。其中期末試卷的題型分布如下:第一大題是填空題,一共6小題,每小題3分,滿分18分,主要考察了定義和重要公式等知識點;第二大題是選擇題,一共4小題,每小題3分,滿分12分,主要考察了相關概念的理解和相關定理的靈活應用能力;第三大題是計算題,一共3小題,每小題10分,滿分30分,主要考察了利用復變函數方法進行計算的能力;第五大題是分析題,滿分14分,主要考察了利用復變函數理論分析和解決問題能力;第一大題、第二大題、第三大題和第五大題對應著課程目標1;第四大題是應用計算題,一共2小題,每小題10分,滿分20分,主要考察了綜合利用復變函數理論解決對應專業問題中的實際問題;第六大題是證明題,滿分6分,主要考察了學術的抽象思維能力和邏輯推理能力;第四大題和第六大題對應著課程目標2。我們統計了全班每位學生每道大題的得分情況,并利用Excel軟件進行了數據分析,得到了如下課程目標達成情況評價信息表:
2 課程目標達成情況分析及存在的問題
表1中的分項評價達成度和總評價達成度的數值范圍都是介于0與1之間,數值越接近于1,說明越接近于全部完成該目標,數值越小,說明完成情況越不好。表1中的標準差越大,代表大部分數值和其平均值之間差異較大,數值越小,說明大部分數值和其平均值之間差異較小。課程目標1主要目的是考查學生運用復變函數相關定義、定理解決簡單問題的能力,其總評價達成度為0.67表明學生基本已經具備該能力。課程目標2主要考查學生運用綜合應用復變函數相關理論解決綜合問題的能力,其總評價達成度為0.3,表明大部分學生不具備該能力。值得注意的是分項評價達成度中第四大題的達成度是0.343,倒數第二,第六大題的達成度是0.135,倒數第一,表明大部分學生只會簡單套公式計算,對知識的綜合應用能力掌握的不好,沒有真正理解相關定義和定理,分析問題和解決問題能力仍不足,有待于進一步的提高。從標準差的結果來看差別比較大的有平時成績、計算題等,說明學生平時的基礎或努力程度差別比較大,需要監督和督促他們的學習。
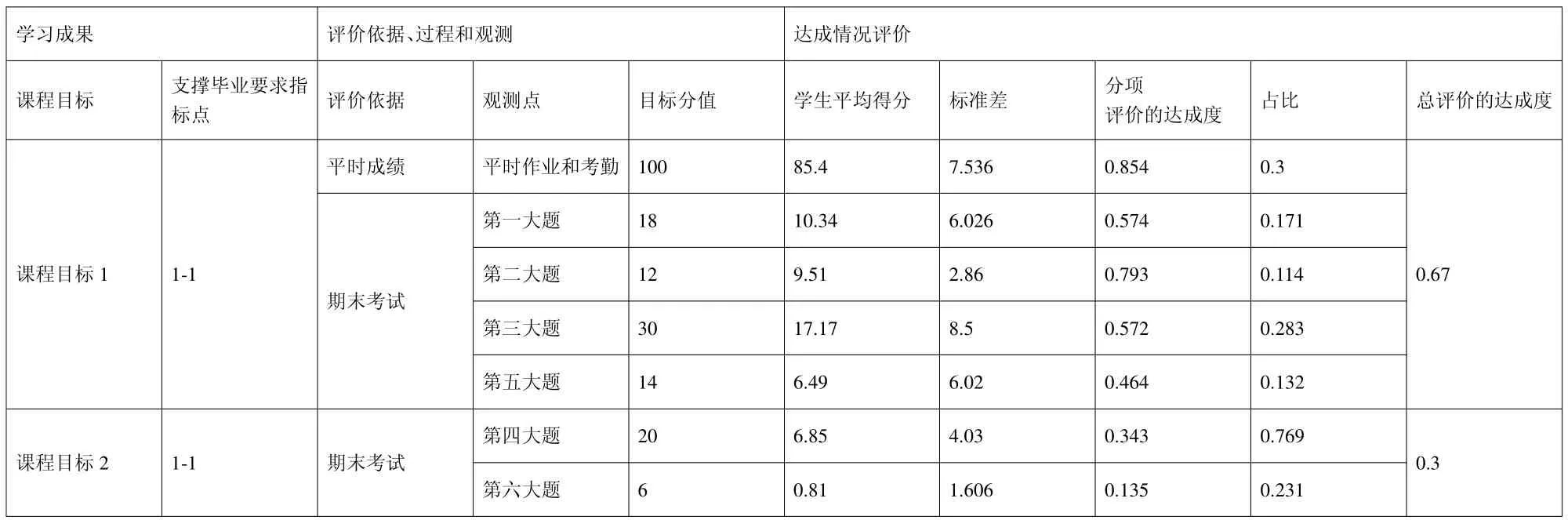
表1:課程目標達成情況評價信息
3 持續改進措施
根據上面的達成度分析,本課程在下面幾個環節進行了改進。
3.1 數學軟件Maple的使用與教材相結合,提升學習興趣
利用Maple軟件進行輔助教學,Maple軟件具有強大的運算、畫圖等功能,可以通過圖形使學生直觀上理解復變函數中抽象的概念,激發學生的學習興趣,培養學生的動手能力。例如,在實變函數中,正弦函數是有界函數且,而在復變函數中正弦函數是無界函數。為了幫助學生理解的無界性,畫出復變函數的圖形如下:
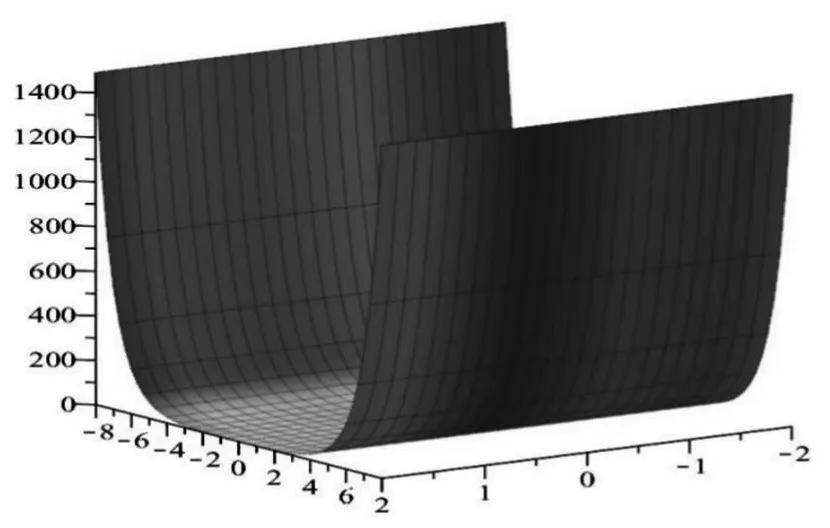
圖1:正弦函數
3.2 挖掘復變函數在工科專業中的應用,增加工程意義
我們主動和本校對應工科專業的專職教師進行討論,討論在哪些專業課程中用到復變函數,具體是哪一部分知識點,并充分利用好圖書館的資源,查閱相關書籍和文獻,深度挖掘復變函數在工科專業中的應用,在講授時根據專業特點,進行了重點講解,從而讓學生自發認為復變函數這門課對他們的后繼專業課學習是有幫助的,復變函數具有重要的工程意義。
3.3 增加課后分層輔導,因材施教
通過上述的達成度分析可以發現,有部分同學基礎薄弱且缺乏努力,完全沒有入門,還有部分同學雖然努力了,但對復變函數許多重要概念和定理一知半解,只是機械式和被動地學習,所以針對不同基礎和學習態度的學生,采取分層輔導方法,輔導內容的深刻和廣度也不一樣,使大家都能積極參與到討論中,都能看見自己的進步。
3.4 融入思政元素,提升育人效果
推進課程思政,形成專業課程和思想政治理論課的協同效應,實現課程的育人功能,是高校教學改革的重要內容。復變函數課程是落實立德樹人根本任務的主要渠道之一,在課程中貫穿能力培養、知識傳授以及價值塑造,構建全課程育人格局,最終實現立德樹人。在課程中,注意將數學史平行融入到教學中,培養學生的科學精神;在學習的過程中,注意比較高等數學與復變函數的區別聯系,將唯物辯證法滲透進教學,培養學生的辯證唯物觀;將社會主義核心價值觀體現在教學各環節中,全面提高學生素質和健全人格;教師講授知識的同時有意識地培養學生刻苦鉆研的精神和創新意識,鼓勵學生多嘗試、多思考、攻堅克難、堅持不懈、勇于創新。

