基于圓周割線改進(jìn)型粒子群優(yōu)化算法的葉片臨界顫振辨識方法研究
李迺璐, 尹佳敏, 楊 華, 朱衛(wèi)軍
(揚(yáng)州大學(xué) 電氣與能源動力工程學(xué)院,江蘇 揚(yáng)州 225127)
風(fēng)力機(jī)葉片在氣動彈性耦合作用下易發(fā)生顫振問題[1],當(dāng)來流風(fēng)速達(dá)到顫振速度時會產(chǎn)生等幅振蕩的臨界穩(wěn)定狀態(tài),即臨界顫振[2-3]。
葉片臨界顫振振動可描述一大類臨界穩(wěn)定的振動現(xiàn)象。對臨界顫振系統(tǒng)辨識的研究,是利用其描述并研究高頻、等幅振動特性,由此監(jiān)測評估葉片的疲勞損傷,并為振動控制設(shè)計(jì)與研究提供模型。
葉片顫振系統(tǒng)本質(zhì)為氣彈系統(tǒng),已有氣彈系統(tǒng)的辨識研究主要集中在航空飛行器氣彈系統(tǒng)的辨識,包括非線性狀態(tài)空間辨識方法[4]、神經(jīng)網(wǎng)絡(luò)辨識方法[5]、ARMA自回歸模型[6]和Hammerstein模型[7]等。這些方法主要針對飛行器氣彈系統(tǒng)進(jìn)行降階辨識和非線性辨識,但是飛行器主要工作在高風(fēng)速、超音速等工況下,而風(fēng)力機(jī)葉片長期工作在低風(fēng)速下,一般最高不超過25 m/s,因此,這些辨識方法并不能直接適用于風(fēng)力機(jī)葉片顫振系統(tǒng)。
目前,葉片振動系統(tǒng)的辨識方法有最小二乘法[8-9]、雙參數(shù)法[10]和自回歸法[11]等,并獲取了良好的辨識精度。然而,這些方法主要針對具有收斂穩(wěn)定性的振動系統(tǒng),還存在實(shí)際應(yīng)用困難、受傳感器安裝角限制等問題。近年,智能優(yōu)化算法,如差分進(jìn)化算法被應(yīng)用到風(fēng)力機(jī)葉片衰減振動系統(tǒng)的參數(shù)辨識[12],進(jìn)步提高了傳統(tǒng)最小二乘法的辨識效果,具有辨識精度高、應(yīng)用性好等優(yōu)點(diǎn)。但智能算法本身的優(yōu)化性能和針對問題的適應(yīng)性,將直接影響辨識結(jié)果。在算法策略、優(yōu)化效率和適用性上還有進(jìn)一步提高的空間。
粒子群優(yōu)化(partical swarm optimization, PSO)算法是一種模擬鳥群覓食行為、基于群體協(xié)作的搜索方法,具有易于實(shí)現(xiàn)、精度高和收斂快等特點(diǎn)[13],被廣泛應(yīng)用于系統(tǒng)辨識、函數(shù)優(yōu)化等領(lǐng)域[14-15]。但PSO算法容易陷入局部最優(yōu),導(dǎo)致計(jì)算結(jié)果與全局最優(yōu)值存在一定誤差。為了提高粒子群優(yōu)化性能,王峰等[16]將粒子群優(yōu)化算法與凹函數(shù)權(quán)值遞減策略相結(jié)合,并通過試驗(yàn)驗(yàn)證了改進(jìn)粒子群優(yōu)化算法的有效性。而基于改進(jìn)型動態(tài)學(xué)習(xí)因子的粒子群優(yōu)化算法(如改進(jìn)型粒子群優(yōu)化(modified particle swarm optimization,MPSO)算法、基于線性遞減慣性權(quán)重的粒子群優(yōu)化(linearly decreasing inertia weight based particle swarm optimization,LDIW-PSO)算法、基于動態(tài)學(xué)習(xí)因子的免疫粒子群優(yōu)化(immune particle swarm optimization based on dynamically changing learning factors,IPSODCLF)算法)也被進(jìn)一步提出并應(yīng)用于典型函數(shù)的極值求解[17-18],風(fēng)光水發(fā)電系統(tǒng)調(diào)度優(yōu)化[19]和Volterra模型辨識[20]等,相比傳統(tǒng)粒子群優(yōu)化算法進(jìn)一步提高了優(yōu)化精度,并改善了陷入局部最優(yōu)的問題。目前,針對葉片臨界穩(wěn)定振動系統(tǒng)的辨識方法研究還較少,值得進(jìn)一步探索和研究。
本文把粒子群優(yōu)化算法引入葉片臨界顫振系統(tǒng)的辨識中,且為了提高算法的尋優(yōu)能力、辨識效率和穩(wěn)定性,創(chuàng)新設(shè)計(jì)了一種全新的改進(jìn)型粒子群優(yōu)化算法:圓周割線改進(jìn)型粒子群優(yōu)化(circular secant modified partical swarm optimization,CSM-PSO)算法。本文在CSM-PSO算法設(shè)計(jì)中,首次引入了幾何圓周割線的距離來自適應(yīng)調(diào)節(jié)學(xué)習(xí)因子,利用圓周角速度來控制調(diào)節(jié)速率,采用學(xué)習(xí)因子的均方和不變策略,有效增強(qiáng)了全局搜索和局部搜索的動態(tài)平衡,避免了優(yōu)化過程中概率性偏重全局搜索或陷入局部最優(yōu),還提高了算法的優(yōu)化效率和穩(wěn)定性。將CSM-PSO算法應(yīng)用于一個典型的葉片臨界顫振系統(tǒng)的辨識仿真試驗(yàn),對比多種改進(jìn)型粒子群優(yōu)化算法的辨識結(jié)果,驗(yàn)證了本文辨識方法在辨識精度、計(jì)算時間和魯棒性方面的優(yōu)越性。
該研究所設(shè)計(jì)的辨識方法,對了解風(fēng)力機(jī)葉片、直升機(jī)葉片和機(jī)翼等系統(tǒng)的臨界穩(wěn)定振動特性、極限環(huán)振頻和振幅分析,以及振動控制、避免耦合結(jié)構(gòu)共振具有實(shí)際意義。
1 圓周割線粒子群優(yōu)化算法
1.1 標(biāo)準(zhǔn)粒子群優(yōu)化算法
粒子群優(yōu)化算法是Kennedy等根據(jù)對鳥群捕食行為提出的一種尋優(yōu)算法。每次迭代過程中,第i個粒子首先找到自己的歷史最優(yōu)解,即局部極值pi,j,進(jìn)而所有粒子依次比較當(dāng)代的最優(yōu)值,找到當(dāng)前的全局極值pg,j。局部極值和全局極值都遵從適應(yīng)度值更小來更新粒子速度和位置,隨著迭代次數(shù)全局最優(yōu)解靠近。
粒子速度和位置更新的公式為
vi,j(k+1)=ω·vi,j(k)+c1r1·[pi,j-xi,j(k)]+c2r2·[pg,j-xi,j(k)]
(1)
xi,j(k+1)=xi,j(k)+vi,j(k+1),j=1,2,3,…,D
(2)
式中:vi,j為粒子速度;xi,j為粒子位置;ω為線性遞減的慣性權(quán)重,表征粒子繼承速度的能力;c1為局部學(xué)習(xí)因子,表征粒子向自身局部極值學(xué)習(xí)的能力;c2為全局學(xué)習(xí)因子,表征粒子向全局極值學(xué)習(xí)的能力;r1,r2分別為兩個[0, 1]內(nèi)的隨機(jī)數(shù)。
粒子群優(yōu)化算法中,種群規(guī)模、迭代次數(shù)、慣性權(quán)重、學(xué)習(xí)因子等參數(shù)都會對尋優(yōu)結(jié)果產(chǎn)生影響。其中,學(xué)習(xí)因子選取不當(dāng)將嚴(yán)重影響算法的尋優(yōu)性能。不適合的c1使粒子缺少向自身歷史軌跡學(xué)習(xí)的能力,只能向種群最優(yōu)學(xué)習(xí),種群會快速集中到一個最優(yōu)解,但是在后期迭代中很難尋找更優(yōu)的解,易陷入局部最優(yōu);不適合的c2使粒子缺乏向種群其他粒子學(xué)習(xí)的能力,粒子偏向單獨(dú)行動,缺少相互交流,無法發(fā)揮種群尋優(yōu)的優(yōu)勢,導(dǎo)致尋優(yōu)速度慢且難以搜索全局最優(yōu)解。
1.2 已有改進(jìn)型粒子群優(yōu)化算法
1.2.1 學(xué)習(xí)因子隨權(quán)重變化的MPSO算法
MPSO算法通過遞減的慣性權(quán)重來調(diào)節(jié)局部學(xué)習(xí)因子和全局學(xué)習(xí)因子,以增強(qiáng)粒子群優(yōu)化算法進(jìn)化時的統(tǒng)一性。MPSO算法采用異步變化的學(xué)習(xí)因子,公式為
c1MPSO=c1s-(c1s-c1e)cosω
c2MPSO=c2s+(c2e-c2s)cosω
(3)
式中:ω為非線性遞減的慣性權(quán)重;c1s和c2s分別為局部學(xué)習(xí)因子c1MPSO和全局學(xué)習(xí)因子c2MPSO的起始值;c1e和c2e分別為局部學(xué)習(xí)因子和全局學(xué)習(xí)因子的終止值。在迭代初期,慣性權(quán)重和局部學(xué)習(xí)因子值較大,全局學(xué)習(xí)因子值較小,種群的全局尋優(yōu)能力較強(qiáng);在迭代后期,慣性權(quán)重和局部學(xué)習(xí)因子值較小,全局學(xué)習(xí)因子值較大,粒子更傾向于向種群中的全局最優(yōu)學(xué)習(xí),使算法更容易得到精確的解。該算法在五種典型測試函數(shù)的優(yōu)化計(jì)算中取得更優(yōu)結(jié)果。
1.2.2 學(xué)習(xí)因子隨迭代次數(shù)變化的LDIW-PSO算法
LDIW-PSO算法為了改善傳統(tǒng)粒子群優(yōu)化算法的早熟收斂問題,利用階段搜索的思想,基于迭代次數(shù)自適應(yīng)調(diào)節(jié)學(xué)習(xí)因子。局部學(xué)習(xí)因子c1LPSO和全局學(xué)習(xí)因子c2LPSO隨迭代次數(shù)的變化公式為
(4)
式中:k為當(dāng)前迭代次數(shù); iter max為最大迭代次數(shù)。當(dāng)1≤k<0.47iter max時,c1LPSO>c2LPSO,局部學(xué)習(xí)因子較大,粒子更多的向個體歷史最優(yōu)學(xué)習(xí),算法的全局尋優(yōu)能力較強(qiáng);當(dāng)0.47iter max
1.2.3 免疫粒子群優(yōu)化算法
針對目前粒子群優(yōu)化算法中存在的易早熟、后期收斂速度慢等問題,免疫粒子群優(yōu)化算法提出了一種動態(tài)調(diào)整學(xué)習(xí)因子的策略。
學(xué)習(xí)因子的更新公式為
c1CPSO=c1max-k(c1max-c1min)/kiter
c2CPSO=c2min+k(c2max-c2min)/kiter
(5)
式中:k為當(dāng)前迭代次數(shù);kiter為最大迭代次數(shù);c1max,c2max分別為局部學(xué)習(xí)因子c1CPSO和全局學(xué)習(xí)因子c2CPSO的最大值;c1min,c2min分別為局部學(xué)習(xí)因子和全局學(xué)習(xí)因子的最小值。通過設(shè)置不同的c1max,c2max,c1min,c2min,可以實(shí)現(xiàn)學(xué)習(xí)因子的非對稱性變化,使粒子早期盡快搜索到較優(yōu)值,后期提高搜索精度,避免算法陷入局部最優(yōu)。該算法利用到風(fēng)光水聯(lián)合系統(tǒng)優(yōu)化調(diào)度模型的仿真計(jì)算中得到了改善的調(diào)度結(jié)果。
1.3 設(shè)計(jì)圓周割線改進(jìn)型粒子群優(yōu)化算法
由于粒子群優(yōu)化算法在葉片振動系統(tǒng)辨識問題中的應(yīng)用較少,如何選取合適的學(xué)習(xí)因子是提高葉片臨界顫振系統(tǒng)辨識性能的關(guān)鍵,而已有改進(jìn)型粒子群優(yōu)化算法并非針對本文問題而設(shè)計(jì)。因此,針對葉片臨界顫振辨識問題,本文首次設(shè)計(jì)了一種基于圓周割線型學(xué)習(xí)因子的新型粒子群優(yōu)化(CSM-PSO)算法。
CSM-PSO算法的核心思路是將幾何圓周割線引入粒子群優(yōu)化算法學(xué)習(xí)因子的動態(tài)調(diào)節(jié)。主要體現(xiàn)在兩個方面:①圓周上的點(diǎn)逆時針繞圓心移動的角速度,定義為學(xué)習(xí)因子的調(diào)節(jié)速率;②圓周上移動的點(diǎn)到水平線上固定點(diǎn)的割線距離,定義為學(xué)習(xí)因子的調(diào)節(jié)數(shù)值。
在學(xué)習(xí)因子的動態(tài)調(diào)節(jié)設(shè)計(jì)中,假設(shè)目標(biāo)函數(shù)值會在某處大幅降低,將此處作為優(yōu)化過程中的一個“分水嶺”,即學(xué)習(xí)因子c1和c2動態(tài)調(diào)節(jié)的交叉點(diǎn),算法在交叉點(diǎn)之前側(cè)重c1,發(fā)揮粒子自身的尋優(yōu)能力;在交叉點(diǎn)之后偏重c2,突出種群的尋優(yōu)能力。基于圓周割線的學(xué)習(xí)因子動態(tài)調(diào)節(jié)原理,如圖1所示。在水平線上取兩個固定點(diǎn)使得OA=OB,將線段MA長度作為局部學(xué)習(xí)因子c1的取值,線段MB長度作為全局學(xué)習(xí)因子c2的取值,圓心角θ的對應(yīng)點(diǎn)M沿圓周逆時針方向運(yùn)動。隨著θ從0°~180°變化,c1逐漸減小,c2逐漸增大,θ=90°時c1=c2,為動態(tài)調(diào)節(jié)中全局尋優(yōu)和局部尋優(yōu)的“分水嶺”。
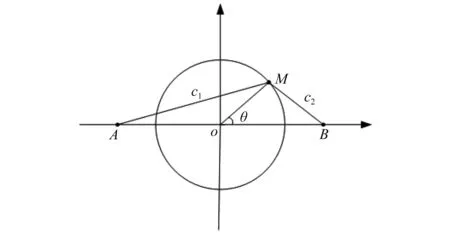
圖1 基于圓周割線的學(xué)習(xí)因子動態(tài)調(diào)節(jié)原理圖
圓心角θ的變化決定學(xué)習(xí)因子的動態(tài)調(diào)節(jié)速率,可表示為
θ=a×t+b×t2
(6)
式中:a,b為系數(shù);t為當(dāng)前迭代次數(shù)k與最大迭代次數(shù)G的比值,t=k/G。設(shè)當(dāng)t=t*時為全局尋優(yōu)和局部尋優(yōu)的“分水嶺”,則存在:①當(dāng)t=0時,θ=0°,c1=cmax,c2=cmin;②當(dāng)t=t*時,θ=90°,c1=c2;③當(dāng)t=1時,θ=180°,c1=cmin,c2=cmax。
基于上述設(shè)計(jì)思想,基于圓周割線的學(xué)習(xí)因子公式為
(7)
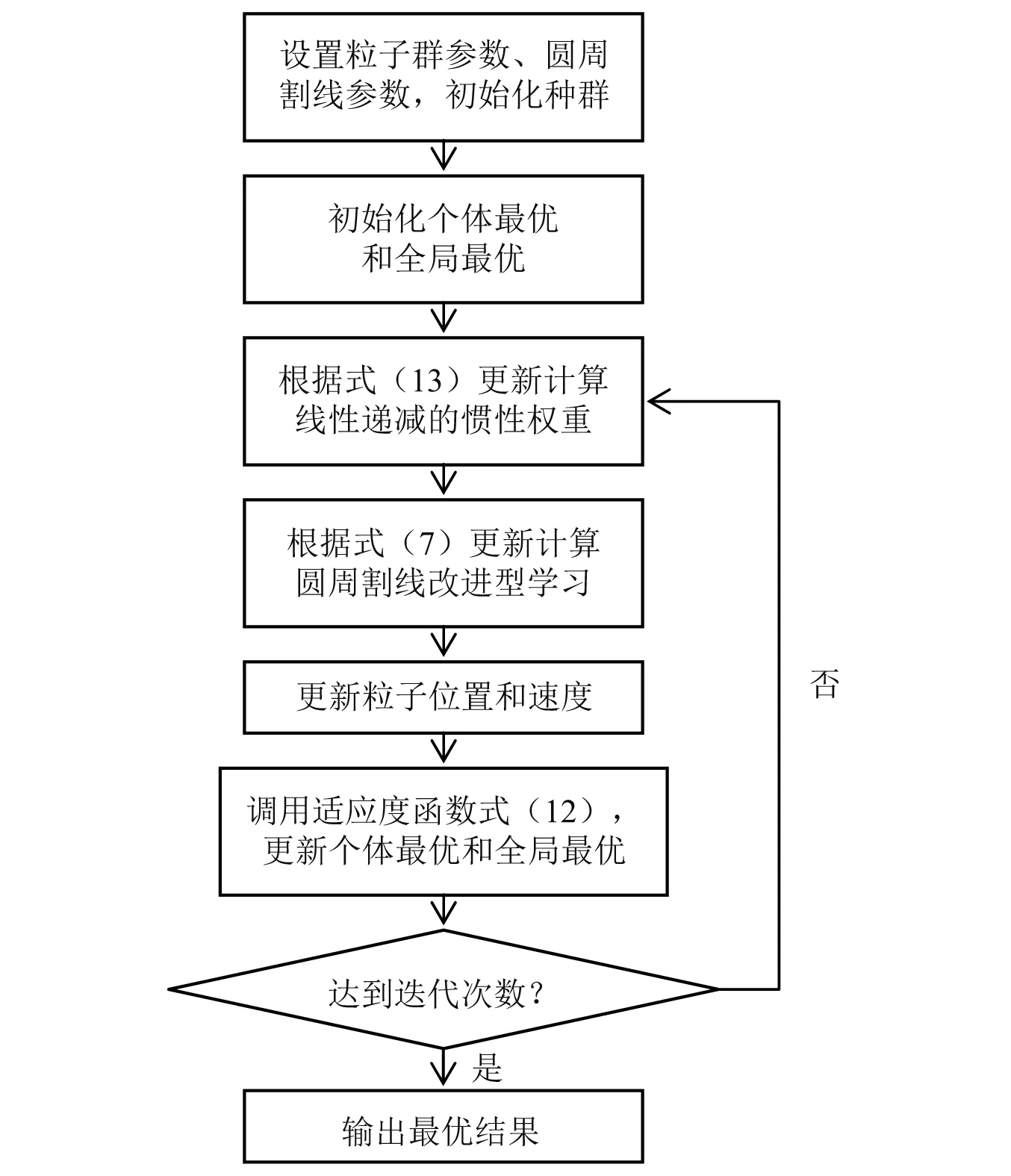
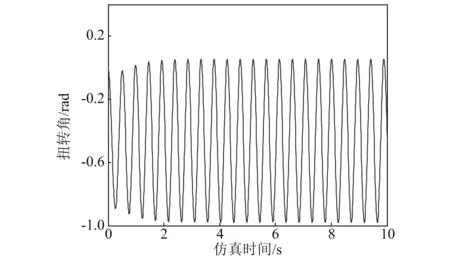
式中,cmax,cmin分別為c1和c2取值范圍的最大值和最小值。當(dāng)k/G 從理論層面,所設(shè)計(jì)CSM-PSO算法的優(yōu)點(diǎn)體現(xiàn)在以下幾個方面: (1) 采用基于圓周角度的非線性調(diào)節(jié)速率,進(jìn)一步增加了學(xué)習(xí)因子調(diào)節(jié)的平滑性,利于實(shí)現(xiàn)全局搜索和局部搜索的動態(tài)平衡; (2) 基于圓周割線的動態(tài)調(diào)節(jié)策略,從原理上使得局部學(xué)習(xí)因子和全局因子具有均方總和不變性,不同于已有方法的總和不變性,利于提高算法的魯棒性; (3) 二維學(xué)習(xí)因子(c1,c2)的調(diào)節(jié)范圍為正方形,克服已有方法的調(diào)節(jié)范圍通常為隨機(jī)長方形,避免概率性過度偏重全局尋優(yōu)或局部尋優(yōu)。 風(fēng)力機(jī)葉片翼型的經(jīng)典顫振模型可表示為 (8) (9) 式中:h為揮舞位移;θ為扭轉(zhuǎn)角;mT為翼型質(zhì)量;xα為質(zhì)心和彈性軸之間的無量綱距離;b為半弦長;Iα為彈性軸轉(zhuǎn)動慣量;ch和cα為阻尼系數(shù);kh和kα為結(jié)構(gòu)剛度;L和M分別為氣動升力和氣動力矩;U為風(fēng)速;ρ空氣密度;clθ,cmθ分別為攻角的氣動升力系數(shù)和氣動力矩系數(shù);clβ,cmβ分別為尾緣襟翼的氣動升力系數(shù)和氣動力矩系數(shù);β為尾緣襟翼角。 (10) 式中: 系統(tǒng)輸出y為扭轉(zhuǎn)角; 系統(tǒng)控制量u為尾緣襟翼角; 系統(tǒng)矩陣A,B,C和D分別為 C=[I2×202×2],D=[02×1]。 其中, 將狀態(tài)空間方程式(10)轉(zhuǎn)化為系統(tǒng)傳遞函數(shù) (11) 式中,a1,a2,a3,b1,b2,b3,b4為葉片顫振系統(tǒng)參數(shù),當(dāng)式(9)中的風(fēng)速U達(dá)到顫振風(fēng)速U*時,式(11)達(dá)到葉片臨界顫振狀態(tài)。 對于葉片臨界顫振系統(tǒng)辨識而言,目的是尋找一組式(11)的系統(tǒng)參數(shù),使得系統(tǒng)輸出與臨界顫振輸出響應(yīng)的誤差最小。 (12) 式中:ts為系統(tǒng)輸出的采樣時間;Nt為采樣個數(shù)。尋優(yōu)目的是最小化適應(yīng)度函數(shù)值,從而獲得最優(yōu)的辨識結(jié)果。辨識算法具體流程為: 步驟1設(shè)置粒子群參數(shù)——粒子位置維度為7,設(shè)置種群規(guī)模S、迭代次數(shù)G等參數(shù); 步驟2設(shè)置圓周割線參數(shù)——設(shè)置t*值并獲取式(6)系數(shù)a,b的值,設(shè)置學(xué)習(xí)因子調(diào)節(jié)范圍cmax,cmin; 步驟3初始化種群——隨機(jī)初始化N個粒子的初始位置,令第i個粒子當(dāng)前位置為個體最優(yōu)位置pi(0),調(diào)用適應(yīng)度函數(shù),適應(yīng)值最小的粒子位置為全局最優(yōu)位置pg(0) 步驟4根據(jù)當(dāng)前迭代次數(shù)k更新計(jì)算慣性權(quán)重ω (13) 步驟5基于圓周割線策略計(jì)算學(xué)習(xí)因子——根據(jù)式(7)計(jì)算全局學(xué)習(xí)因子c2和局部學(xué)習(xí)因子c1; 步驟6更新粒子位置和速度——根據(jù)式(1)和式(2),更新粒子的速度及位置,產(chǎn)生新種群; 步驟7更新個體最優(yōu)——調(diào)用適應(yīng)度函數(shù),比較粒子的當(dāng)前適應(yīng)值J(Xi)和自身歷史最優(yōu)pi,如果J(Xi) 步驟8更新全局最優(yōu)——比較粒子當(dāng)前適應(yīng)值J(Xi)與種群最優(yōu)值pg,如果J(Xi) 步驟9重復(fù)步驟4~步驟8的,直到達(dá)到迭代要求,結(jié)束并輸出最終結(jié)果。 基于CSM-PSO的葉片臨界顫振系統(tǒng)辨識算法流程,如圖2所示。 圖2 基于CSM-PSO的葉片臨界顫振辨識算法流程圖 仿真試驗(yàn)以基于NACA0012翼型的葉片振動系統(tǒng)為研究對象,模型參數(shù)如表1所示。利用表1參數(shù)和軟件MATLAB/Simluink進(jìn)行顫振仿真試驗(yàn),當(dāng)風(fēng)速增至9.6 m/s時,可觀察到等幅振蕩響應(yīng),如圖3所示,即為臨界顫振現(xiàn)象。因此,根據(jù)顫振速度U*=9.6 m/s和表1參數(shù),可獲取葉片臨界顫振模型為 圖3 葉片臨界顫振響應(yīng) 表1 基于NACA0012翼型的模型參數(shù)表 G(s)= (14) 將式(14)作為目標(biāo)辨識模型,為四階傳遞函數(shù),包含7個待辨識的系統(tǒng)參數(shù)。臨界顫振模型辨識的困難存在以下幾個方面:①待辨識參數(shù)的量級差別較大,從101~104,不利于所有參數(shù)的精確辨識;②葉片臨界顫振狀態(tài)對應(yīng)的系統(tǒng)參數(shù)具有唯一性,任意一個參數(shù)辨識誤差較大,都無法正確辨識出臨界顫振特性;③由于臨界顫振為等幅振蕩,本質(zhì)上為臨界穩(wěn)定系統(tǒng),該類系統(tǒng)普遍較難精確辨識。 利用本文設(shè)計(jì)的CSM-PSO算法對式(11)所示葉片臨界顫振模型的參數(shù)進(jìn)行辨識,種群規(guī)模為100,最大迭代次數(shù)為150,系統(tǒng)辨識的測試重復(fù)20次,結(jié)果取平均值。CSM-PSO算法的應(yīng)用中,設(shè)t*=k/G=0.25,得到式(6)系數(shù)為a=7.330 4,b=-4.188 8,學(xué)習(xí)因子范圍為cmax=2.5,cmin=0.2。 辨識試驗(yàn)主要從4個方面開展研究:①合適的辨識輸入信號;②本文CSM-PSO算法的辨識精度;③CSM-PSO算法的辨識計(jì)算成本;④CSM-PSO辨識算法的魯棒性。上述試驗(yàn)將與已有改進(jìn)型粒子群優(yōu)化算法的辨識結(jié)果進(jìn)行對比研究。 3.3.1 輸入信號 辨識要求持續(xù)激勵的輸入信號,本文分別采用白噪聲、M序列作為辨識的輸入信號進(jìn)行試驗(yàn)。白噪聲輸入為[0,1]內(nèi)的均勻白噪聲信號,M序列輸入為基于8個移位寄存器、幅值為1的M序列信號。 兩種輸入信號下的平均適應(yīng)度函數(shù)進(jìn)化曲線,如圖4所示,白噪聲輸入信號下的進(jìn)化曲線收斂慢,并存在較大辨識誤差;而采用M序列輸入信號可以獲取較為精確的辨識結(jié)果。因此,傳統(tǒng)白噪聲輸入信號并不適用于本文臨界顫振辨識問題,而采用M序列時辨識誤差更小、收斂速度更快,是本文臨界顫振振動系統(tǒng)辨識比較合適的輸入信號。 圖4 不同輸入信號下的Jave進(jìn)化曲線 3.3.2 辨識精度 表2為M序列輸入信號下,本文的CSM-PSO算法以及已有改進(jìn)型粒子群優(yōu)化算法(如MPSO, LDIW-PSO, IPSODCLF)所得到的臨界顫振系統(tǒng)參數(shù)的辨識值、適應(yīng)度函數(shù)平均值Jave和均方根Jsd,表2中真值來自式(14)系統(tǒng)參數(shù)。 表2 不同算法下的葉片臨界顫振系統(tǒng)辨識結(jié)果 由表2可知,已有改進(jìn)型粒子群優(yōu)化算法獲得的辨識誤差較大,同時MPSO和LDIW-PSO算法辨識存在較大的均方根誤差,說明針對臨界顫振系統(tǒng),已有先進(jìn)粒子群優(yōu)化算法難以實(shí)現(xiàn)精確、穩(wěn)定的辨識。而本文所設(shè)計(jì)的CSM-PSO算法,在有限的種群規(guī)模和迭代次數(shù)下,辨識值更接近真值,其辨識精度明顯較高、其辨識穩(wěn)定性也顯著優(yōu)于其他算法。 圖5給出了四種辨識方法分別得到的平均適應(yīng)度函數(shù)的進(jìn)化曲線。由圖5中可知,CSM-PSO算法的收斂速度較快,并獲取了較為滿意的辨識精度;在有限迭代次數(shù)下,已有改進(jìn)型粒子群優(yōu)化算法收斂較慢,且難以搜尋全局最優(yōu)值并陷入局部值。因此,相較下CSM-PSO算法明顯改善了全局搜索能力、局部搜索能力和搜索過程中的動態(tài)平衡,在整個進(jìn)化辨識中體現(xiàn)了較強(qiáng)的尋優(yōu)性能、避免了陷入局部最優(yōu),實(shí)現(xiàn)了葉片臨界顫振系統(tǒng)參數(shù)的高精度辨識。圖6給出了辨識模型和真實(shí)模型的響應(yīng)對比。 圖5 不同算法的Jave進(jìn)化曲線 圖6 系統(tǒng)辨識響應(yīng)對比 3.3.3 計(jì)算時間 表3給出了多種辨識算法的計(jì)算時間和適應(yīng)度函數(shù)值。針對MPSO, LDIW-PSO和IPSODCLF辨識算法,設(shè)置種群S=100,迭代次數(shù)G=200,針對CSM-PSO算法設(shè)置S=100,G=100。 由表3可知,CSM-PSO算法在100次迭代下就可獲得精確的辨識結(jié)果。在辨識時間方面,CSM-PSO算法明顯降低了平均計(jì)算時間,表明了其優(yōu)越的計(jì)算性能。對比表2結(jié)果,當(dāng)?shù)螖?shù)增加至200,MPSO, LDIW-PSO和IPSODCLF算法的平均適應(yīng)度函數(shù)值有所改善,但是整體辨識誤差依舊大于0.1。綜上,已有改進(jìn)型粒子群優(yōu)化算法不僅花費(fèi)的計(jì)算時間長,辨識效果也不佳。而本文所設(shè)計(jì)的CSM-PSO算法不僅辨識精度較高,還具有較低的計(jì)算成本。 表3 不同算法的辨識計(jì)算時間 3.3.4 魯棒性 為了驗(yàn)證本文CSM-PSO算法的魯棒性,對比多種已有算法,表4給出了20次運(yùn)行,種群規(guī)模100和迭代次數(shù)150下的適應(yīng)度函數(shù)值統(tǒng)計(jì)分析結(jié)果,包括最大值Jmax,最小值Jmin,平均值Jave、中間值Jmedi和均方差值Jsd。圖7和圖8分別給出了最大適應(yīng)值和最小適應(yīng)值的進(jìn)化曲線。 由圖7可知,辨識最差情況下,CSM-PSO算法仍可獲取較高的辨識精度、較快的收斂速度,而其他算法均存在較大辨識誤差。由圖8可知,辨識最好情況下,CSM-PSO算法可在80次迭代后獲取高精度的辨識結(jié)果,而其他三種算法此時未收斂或陷入局部最優(yōu)值。 圖7 不同算法的Jmax進(jìn)化曲線 圖8 不同算法的Jmin進(jìn)化曲線 由表4可知, CSM-PSO算法的各方面統(tǒng)計(jì)結(jié)果,都顯著優(yōu)越于其他三種已有算法,特別是適應(yīng)度函數(shù)的均方差值、最大值和最小值,說明CSM-PSO算法明顯提高改善了算法的魯棒性、穩(wěn)定性和收斂性。 表4 不同算法的辨識魯棒性分析 本文設(shè)計(jì)了圓周割線改進(jìn)型粒子群優(yōu)化算法,引入葉片臨界顫振系統(tǒng)的參數(shù)辨識中,并在仿真試驗(yàn)中,將該辨識方法與基于MPSO,LDIW-PSO和IPSODCLF算法的辨識方法進(jìn)行了對比分析。研究結(jié)果表明,與其他三種算法相比,提出的方法在辨識精度、計(jì)算時間和魯棒性方面都具有顯著的優(yōu)越性。本文提出的方法,創(chuàng)新性地利用幾何圓周割線來設(shè)計(jì)粒子群優(yōu)化算法學(xué)習(xí)因子的動態(tài)調(diào)節(jié)策略,具有避免概率性偏重全局或局部尋優(yōu)、利于全局搜索和局部搜索的動態(tài)平衡、算法穩(wěn)定性強(qiáng)和尋優(yōu)效率高的優(yōu)點(diǎn)。本文設(shè)計(jì)的CSM-PSO算法及其在葉片臨界顫振系統(tǒng)辨識中的應(yīng)用,為臨界穩(wěn)定振動系統(tǒng)辨識提供了一種全新、高效、穩(wěn)定的辨識方法,具有重要的理論價值和應(yīng)用價值。2 葉片臨界顫振系統(tǒng)辨識
2.1 葉片翼型振動模型
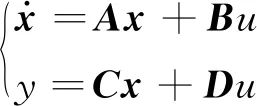
2.2 基于CSM-PSO的臨界顫振辨識算法流程

3 仿真研究
3.1 葉片臨界顫振辨識問題
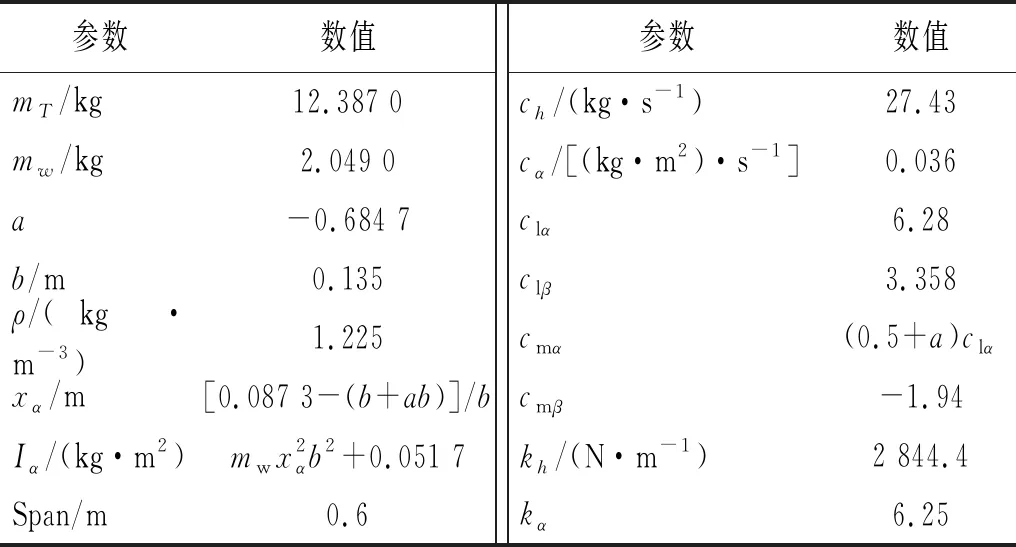
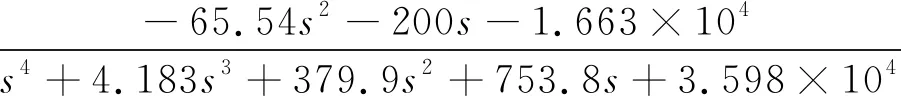
3.2 CSM-PSO算法的辨識應(yīng)用
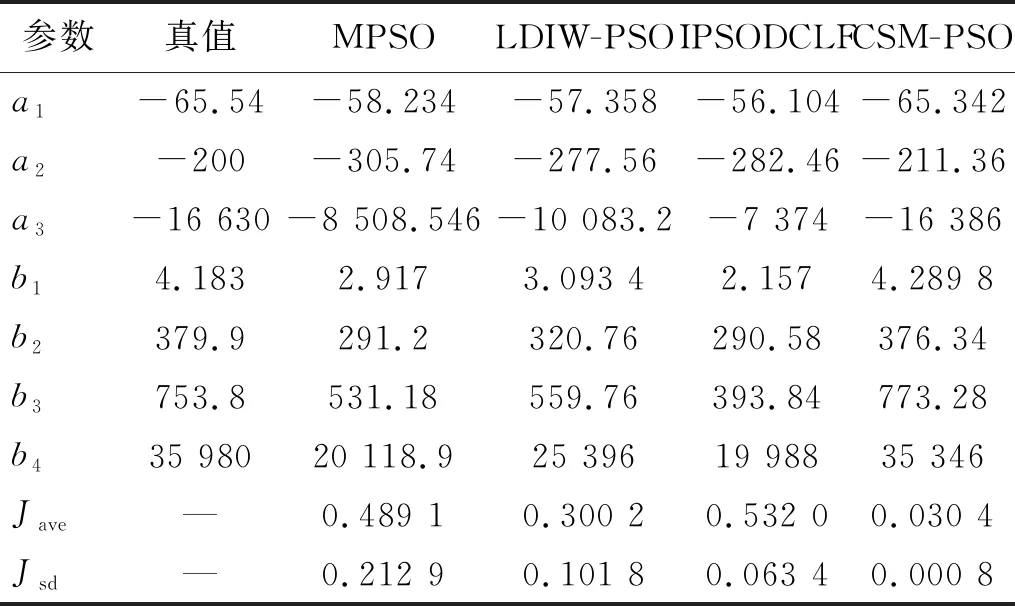
3.3 辨識結(jié)果


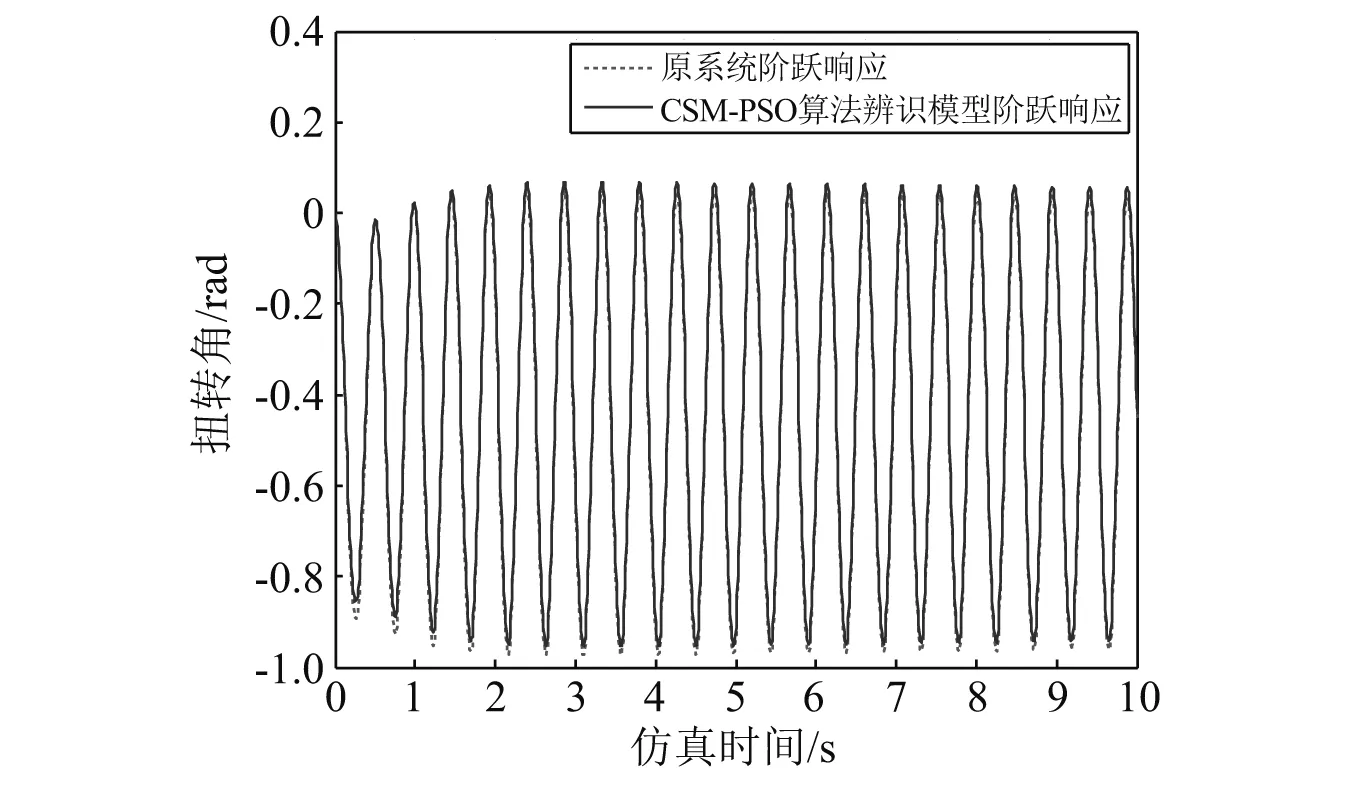

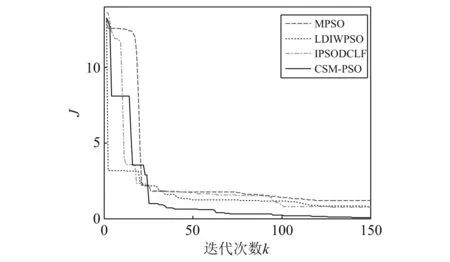
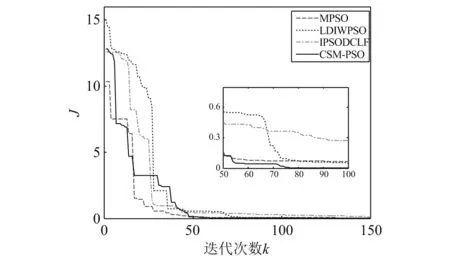

4 結(jié) 論

