均壓槽氣體靜壓軸承數值計算與靜態性能分析*

王 婷 張 浩 楊佳成 陸晨飛

(1.南京工業大學機械與動力工程學院 江蘇南京 211800；2.江蘇省工業裝備數字制造及控制技術重點實驗室 江蘇南京 211800)

氣體靜壓軸承具有運動精度高、摩擦小、無污染、發熱低等優點，是超精密制造領域的重要設備，在航空航天、IT芯片制造業、超精密裝備制造業和國防應用裝備制造業中得到了廣泛的應用。由于氣體的可壓縮性，導致提高氣體靜壓軸承的承載力和剛度變得困難[1]。因此，高剛度和高承載能力的氣體靜壓軸承研究，近年來受到學者的廣泛關注。LU等[2]研究了多孔集成節流方式對氣體靜壓軸承的承載力和剛度的影響。GAO等[3]利用CFD方法分析了6種不同形狀的氣腔對氣體靜壓軸承性能的影響，并進行了實驗驗證。NISHIO等[4]通過數值分析與實驗研究證明了與均壓槽相比，直徑小于0.05 mm的節流孔可以使軸承獲得更高的剛度和更大的阻尼系數。

通過在軸承表面設計均壓腔和槽結構，改變軸承氣膜的壓力分布，是提高氣體靜壓軸承承載性能的重要方式之一[5]。YAN等[6]提出了6種不同結構的均壓槽，并分析它們對氣體靜壓導軌承載性能的影響，結果表明均壓槽可以大幅度提高導軌的承載力和剛度。GAO等[7]研究了具有不同參數的人字槽對高速主軸的氣體靜壓軸承承載性能的影響。DU等[8]研究了均壓槽的開設形式及結構參數對氣體軸頸軸承承載力和剛度的影響。GUENAT和SCHIFFMANN[9]研究了螺旋槽對氣體止推軸承承載性能的影響。王茜等人[10]研究了雙環聯結形均壓槽的尺寸對氣體靜壓導軌承載力和剛度的影響。ZHAO等[11]研究了彈性均壓槽的尺寸對氣體靜壓止推軸承承載力、剛度和質量流量的影響，并進行了實驗驗證。于普良等[5]提出了一種徑向均壓槽結構氣體靜壓軸承，研究表明均壓槽的結構對軸承承載能力和剛度有顯著影響。CHEN和LIN[12]提出了一種十字型均壓槽，分析其結構參數對氣體靜壓止推軸承的承載力和剛度的影響，并通過實驗進行了驗證。

關于機床氣浮導軌上氣體靜壓軸承承載性能的研究較少，因此本文作者在微小型精密機床的氣體靜壓軸承的工作面上設計了橫截面為矩形的直線形均壓槽。結構復雜的均壓槽會使氣膜中的氣體體積增多，容易導致軸承的氣錘自激振動[13]，直線形均壓槽的結構更簡單，穩定性更好。文中主要研究了均壓槽的深度和寬度、節流孔的直徑、高度和個數以及供氣壓力對氣體靜壓導軌靜態性能的影響。經過仿真計算分別得到軸承頂部和底部氣膜的壓力分布及質量流量，綜合考慮軸承頂部和底部氣膜對其總體承載性能的影響，利用差膜計算的方法得到了軸承的承載力和剛度。分析不同結構參數下軸承質量流量、承載力和剛度的變化規律并進行最佳性能參數的優化。

1 物理模型

簡化后微小型精密機床的氣體靜壓導軌模型如圖1所示，主要由導軌、滑塊、節流裝置等組成。在工作狀態下，外部氣源設備產生的高壓氣體通過進氣口被引入氣浮導軌滑塊內部的多個氣路通道，在流經節流孔和均壓槽后進入導軌與滑塊的潤滑間隙，形成具有承載力和剛度的薄膜，從而起到潤滑軸承與支撐外部載荷的作用，最后氣體從軸承端部流出。

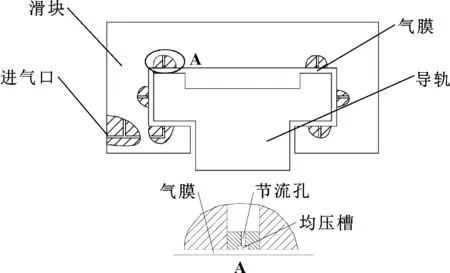
圖1 氣體靜壓導軌模型簡圖

由圖1可知，軸承兩側的氣膜對軸承的承載性能幾乎不起作用，因此文中只對軸承頂部和底部4個部分的氣膜進行分析。每個軸承間隙都均勻分布有節流孔，在節流孔的出口處設計有截面形狀為矩形的直線形均壓槽。以6個節流孔的氣體靜壓軸承為例，其頂部左端的氣膜模型如圖2所示，節流孔中心與軸承滑塊左側的距離為F，與滑塊右側的距離為E，導軌兩側的氣膜結構完全對稱。氣膜的尺寸參數如表1所示。

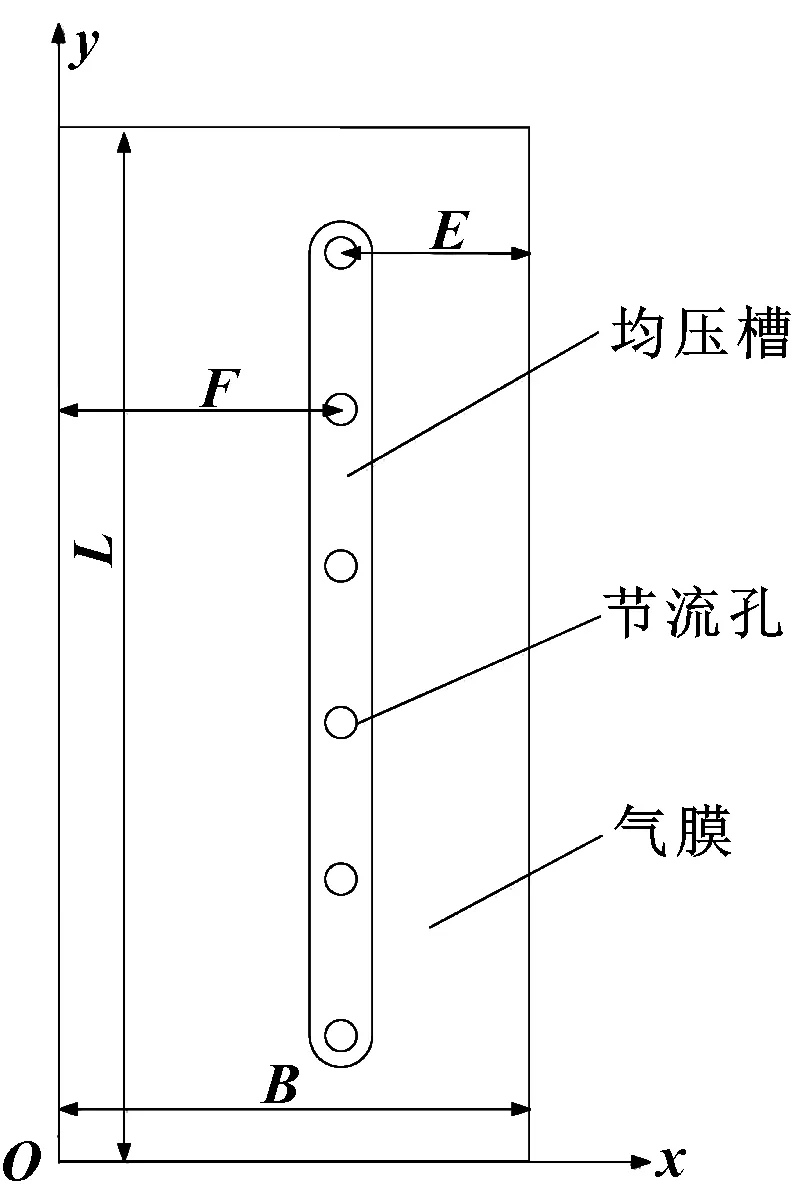
圖2 軸承頂部左端氣膜模型

表1 氣膜的尺寸參數

2 控制方程

為通過計算求解氣膜表面的壓力分布，得到氣膜的承載力、剛度和質量流量，需做如下假設[14-15]：

(1)內部的氣體為牛頓流體；

(2)內部的氣體為連續介質；

(3)內部的氣體為單相介質；

(4)內部的氣體在流動過程中等溫；

(5)氣膜流出的氣體質量流量等于從節流孔進入的氣體質量流量。

可壓縮流體的連續性方程[16]:

(1)

式中：ρ為氣體密度；a為均壓槽截面的高度；u為氣體在x方向的速度；v為氣體在y方向的速度；w為氣體在z方向的速度。

等溫氣體狀態方程[6]:

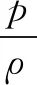
(2)

式中：p為氣體絕對壓力；R為氣體常數；g為重力加速度；T為氣體絕對溫度。

氣膜上各點的壓力分布滿足雷諾方程[17]:

(3)

式中：h為氣膜厚度；p0為供氣壓力;Q為流量因子；δi為狄克拉函數。

由圖1可知，在工作狀態下，由于受到載荷的作用，軸承頂部的氣膜被擠壓變薄，底部的氣膜被拉伸變厚。F1和F2分別代表頂部和底部氣膜的氣膜力，W代表軸承的承載力。施加在滑塊上方的力F1與重力方向相反，施加在滑塊下方的力F2與重力方向相同，因此，為了實現支撐的作用，應滿足F1>F2，根據差膜計算方法，軸承的承載力可表示為

W=F1-F2

(4)

根據流體潤滑理論，軸承氣膜間隙的流體流動應該與各個節流孔入口處的流體流動相平衡，并滿足流量平衡方程：

Qin=Qout

(5)

其中，Qin是通過節流孔進入氣膜間隙的流量，通過下式計算得到：

(6)

(7)

從氣膜邊緣流出的氣體質量流量為

(8)

式中:n為節流孔的個數；A是節流孔的橫截面積；Φ是考慮真實流量與理論流量的差異常數；ρ0為供氣密度；Ψ為噴嘴的流速系數；k為傳熱系數；p為止推面上的壓力；μ為氣體的黏度；B為氣膜的寬度；L為氣膜的長度；ρa是外部環境中氣體的密度。

通過對軸承頂部和底部的氣膜分別進行仿真計算，得到氣膜工作面的壓力分布。軸承承載力的計算公式如下：

(9)

式中：S1是頂部氣膜面積；S2是底部氣膜面積。

軸承受到外載荷作用時頂部和底部氣膜的厚度會產生同等大小的尺寸變化，假定變化量為Δh,則根據偏心率e,可以得到軸承在不同偏心率下的剛度，偏心率的計算公式為

e=Δh/h0

(10)

剛度的計算公式為

K=ΔW/Δh

(11)

式中：h0為氣膜初始厚度；ΔW為承載力的變化量；Δh為氣膜厚度的變化量。

從節流孔進入軸承氣膜間隙的氣體質量流量為Qin，所以從氣膜間隙流出的總氣體質量流量的計算公式為

M=Qin1+Qin2

(12)

式中：Qin1為從頂部氣膜的節流孔進入的質量流量；Qin2為從底部氣膜的節流孔進入的質量流量。

3 邊界條件及氣膜結構

由于氣膜是完全對稱的結構，因此為了提升計算速度，取其1/2進行仿真分析。以6個節流孔的軸承為例，其氣膜結構如圖3所示。設置氣膜入口為壓力入口，出口為壓力出口，出口處壓力pd=101 325 Pa，設置氣膜剖面為對稱面，其余面為壁面，計算模型采用κ-ε模型，其他參數為默認值。

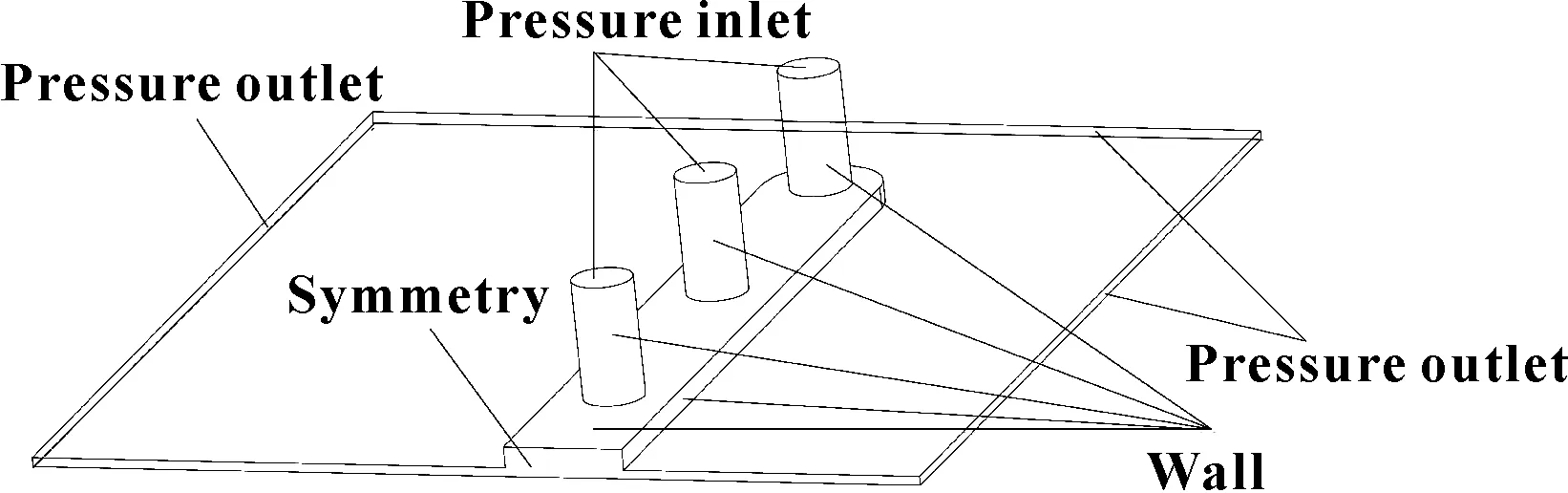
圖3 氣膜計算模型

κ-ε湍流模型的標準方程為

ρε-YM+Sκ

(13)

(14)

式中：κ為湍動能；ε為耗散率；ui為時均速度；μt為湍動黏度；σκ和σε分別是湍動能κ和耗散率ε對應的Prandtl數；Gκ是由于平均速度梯度引起的湍動能κ的產生項;Gb是由于浮力引起的湍動能κ的產生項；YM代表可壓湍流中脈動擴張的貢獻；C1ε、C2ε、C3ε為經驗常數；Sκ和Sε是用戶定義的源項。

4 數值仿真方法正確性驗證

為驗證數值仿真計算的正確性，對文獻[18]中的氣浮軸承模型進行層流仿真計算，并將仿真計算結果與文獻[18]中的計算結果進行比較。文獻[18]中的氣浮軸承模型如圖4所示，節流孔半徑R1=0.25 mm，軸承半徑R2=5 mm，氣膜厚度h=6.3 μm，節流孔高度l=1 mm，入口壓力ps=0.49 MPa，出口壓力pd=0，氣體設置為理想氣體，氣體溫度為293 K，計算結果和實驗結果如圖5所示。可以看出，層流仿真計算的結果與文獻[18]中的實驗結果基本一致，說明對氣體靜壓軸承的層流仿真計算是正確可靠的。

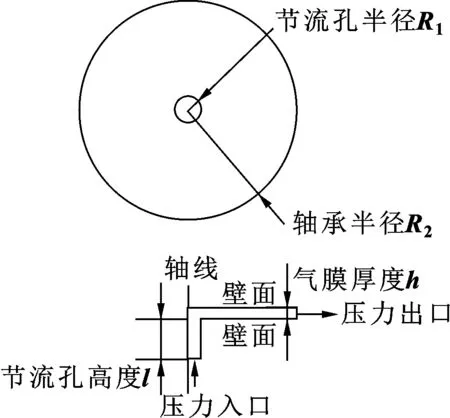
圖4 氣體靜壓軸承結構示意

圖5 層流模型仿真結果和實驗結果對比

5 均壓槽氣體靜壓軸承靜態性能分析

為研究均壓槽對氣體靜壓軸承承載力的影響，對設計有均壓槽的氣體靜壓軸承和沒有均壓槽的氣體靜壓軸承頂部的氣膜模型進行了仿真計算。模型結構尺寸如表1所示，模型的其余參數如表2所示，計算得到的氣膜壓力云圖如圖6所示。

表2 模型計算參數

圖6示出了有均壓槽與無均壓槽的軸承氣膜壓力分布。可以看出，與無均壓槽的軸承相比，增加了均壓槽的軸承氣膜壓力明顯提高，并且壓力分布更加均勻。圖7示出了有均壓槽與無均壓槽的軸承沿節流孔排列方向的氣膜壓力曲線。可以看出，無均壓槽軸承的氣膜只在節流孔附近氣壓較高，遠離節流孔的氣膜壓力急劇下降，最低只有0.13 MPa左右，氣膜邊緣的壓力迅速降低至外部環境壓力；有均壓槽軸承的氣膜壓力在節流孔處壓力最高，在遠離節流孔的均壓槽范圍內氣膜壓力幾乎沒有明顯降低，在沒有均壓槽的氣膜邊緣處壓力降低至最低值時也較為緩慢。因此，增加均壓槽可以有效減小氣膜壓降，提高氣體靜壓軸承的承載力。

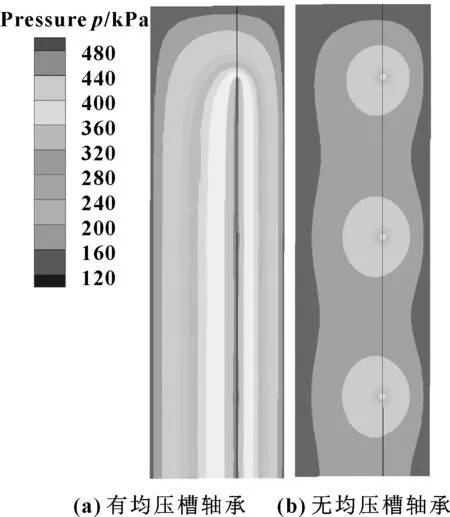
圖6 有無均壓配槽軸承氣膜壓力云圖對比

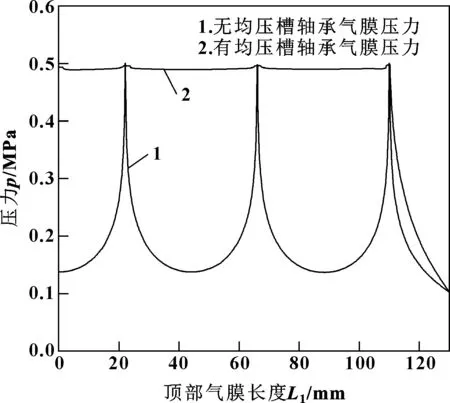
圖7 氣膜沿節流孔排列方向壓力分布

5.1 均壓槽深度對軸承承載性能的影響

在均壓槽寬度b=0.6 mm，節流孔直徑d=0.2 mm，節流孔高度l=0.5 mm，節流孔個數m=6,供氣壓力ps=0.5 MPa的條件下，研究均壓槽深度a分別為0.1、0.15、0.2、0.25、0.3 mm時對均壓槽氣體靜壓軸承的承載力W、剛度K和質量流量M的影響。計算結果如圖8所示。

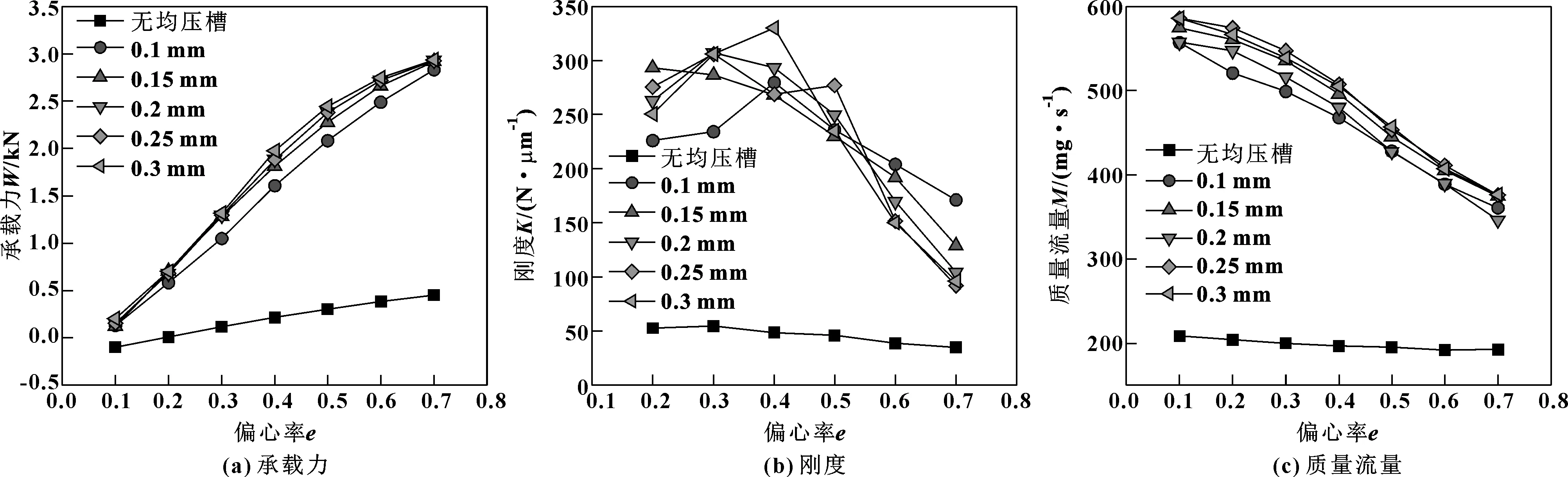
圖8 均壓槽深度對軸承承載力、剛度和質量流量的影響

由圖8(a)可知，同一均壓槽深度下，隨著偏心率的增大，軸承的承載力不斷提高，并且承載力的提升速度逐漸變慢；同一偏心率下，槽深值越大，對應的承載力越高；當0.3≤e≤0.6時，槽深值越大，對承載力的提升效果越明顯，其他偏心率下，不同的槽深對承載力的影響不大，這說明當氣膜厚度適中時,增加槽深值對氣膜壓力的提升效果最好，氣膜厚度過大或者過小，增加槽深值對氣膜壓力的提升效果會變差；有均壓槽的軸承承載力最大約為無均壓槽的6.5倍，隨著偏心率的增大，有均壓槽軸承承載力的提升幅度也越大，這說明氣膜厚度越小，均壓槽對承載力的提升效果越明顯。

由圖8(b)可知，除均壓槽深度為0.15 mm的軸承剛度隨著偏心率的增大逐漸減小之外，其余槽深對應的剛度隨著偏心率的增大先增大后減小；具有不同槽深的軸承處于最大剛度時對應著不同的偏心率；當e>0.5時，槽深值越大，對應的剛度值越小；有均壓槽的軸承剛度最大約為無均壓槽的6.8倍。

由圖8(c)可知，同一均壓槽深度下，隨著偏心率的增大，軸承的氣體質量流量減小；總體來看，同一偏心率下，槽深值越大，其對應的質量流量也越大；有均壓槽的軸承質量流量最大約為無均壓槽的2.8倍。

綜上所述，增加均壓槽可以顯著提升軸承的承載力和剛度，但槽深不宜過大，否則會減弱均壓槽對剛度的提升效果，并且會增大軸承的耗氣量。所以槽深的最佳值為a=0.2 mm。

5.2 均壓槽寬度對軸承承載性能的影響

在均壓槽深度a=0.2 mm，節流孔直徑d=0.2 mm，節流孔高度l=0.5 mm，節流孔個數m=6,供氣壓力ps=0.5 MPa的條件下，研究均壓槽寬度b分別為0.3、0.4、0.5 、0.6、0.7 mm時對軸承的承載力W、剛度K和質量流量M的影響。計算結果如圖9所示。

圖9 均壓槽寬度對軸承承載力、剛度和質量流量的影響

由圖9(a)可知，同一均壓槽寬度下，隨著偏心率的增大，軸承的承載力不斷提高，并且承載力的提升速度逐漸變慢；同一偏心率下，槽寬值越大，對應的承載力越高，但差別不明顯，這說明增加槽寬對氣膜壓力的提升效果不大；有均壓槽的軸承承載力最大約為無均壓槽的6.7倍。

由圖9(b)可知，同一均壓槽寬度下，除b=0.7 mm對應的軸承剛度在e=0.3處出現波動外，其余寬度下的剛度隨著偏心率的增大先增大后減小；不同槽寬的軸承最大剛度值都集中于偏心率為0.3和0.4處；同一偏心率下，e<0.4時，增大槽寬值，軸承的剛度減小；e≥0.4時，適當增大槽寬值可以提高剛度，但b>0.5 mm時剛度減小；有均壓槽的軸承剛度最大約為無均壓槽的6.5倍。

由圖9(c)可知，同一均壓槽寬度下，隨著偏心率的增大，軸承的氣體質量流量減小；同一偏心率下，槽寬較小時，對應的氣體質量流量較大，隨著槽寬的增大，氣體質量流量減小，但是當槽寬增大到0.7 mm時，氣體質量流量又會變大；有均壓槽軸承的質量流量最大約為無均壓槽的2.8倍。

綜上所述，增大槽寬值可以提高承載力，但效果不明顯；偏心率較大時，增大槽寬值可以提高軸承剛度，但槽寬不能超過0.5 mm。所以槽寬的最佳值為b=0.4 mm。

5.3 節流孔直徑對軸承承載性能的影響

在均壓槽深度a=0.2 mm，均壓槽寬度b=0.4 mm,節流孔高度l=0.5 mm，節流孔個數m=6,供氣壓力ps=0.5 MPa的條件下，研究節流孔直徑d分別為0.1、0.15、0.2、0.25、0.3 mm時對均壓槽復合節流氣體靜壓軸承的承載力W、剛度K和質量流量M的影響。計算結果如圖10所示。

由圖10(a)可知，同一節流孔直徑下，隨著偏心率的增大，軸承的承載力不斷提高，除d=0.1 mm之外，其余孔徑對應的承載力提升速度逐漸變慢；偏心率e<0.4時，在同一偏心率下，孔徑越大，對應的承載力越高；偏心率e≥0.4時，隨著偏心率的增大，孔徑越小，承載力的提升速度越快。這說明當氣膜厚度較大時，較大的節流孔直徑對承載力的提升效果更好，氣膜厚度較小時，則相反。

由圖10(b)可知，同一節流孔直徑下，隨著偏心率的增大，除d=0.1 mm的軸承剛度越來越大之外，其余孔徑對應的剛度先增大后減小；當偏心率e<0.4時，同一偏心率下，孔徑越大，其對應的剛度越大；當偏心率e>0.4時，同一偏心率下，孔徑越大，其對應的剛度反而越小。

由圖10(c)可知，同一節流孔直徑下，隨著偏心率的增大，軸承的氣體質量流量逐漸減小；同一偏心率下，增大孔徑，氣體質量流量明顯增大。

圖10 節流孔直徑對軸承承載力、剛度和質量流量的影響

綜上所述，偏心率較小時，增大節流孔直徑可以提高軸承的承載力和剛度，但是會導致耗氣量急劇增加。所以節流孔直徑的最佳值為d=0.2 mm。

5.4 節流孔高度對軸承承載性能的影響

在均壓槽深度a=0.2 mm，均壓槽寬度b=0.4 mm，節流孔直徑d=0.2 mm，節流孔個數m=6,供氣壓力ps=0.5 MPa的條件下，研究節流孔高度l分別為0.4、0.5、0.6、0.7、0.8 mm時對軸承的承載力W、剛度K和質量流量M的影響。計算結果如圖11所示。

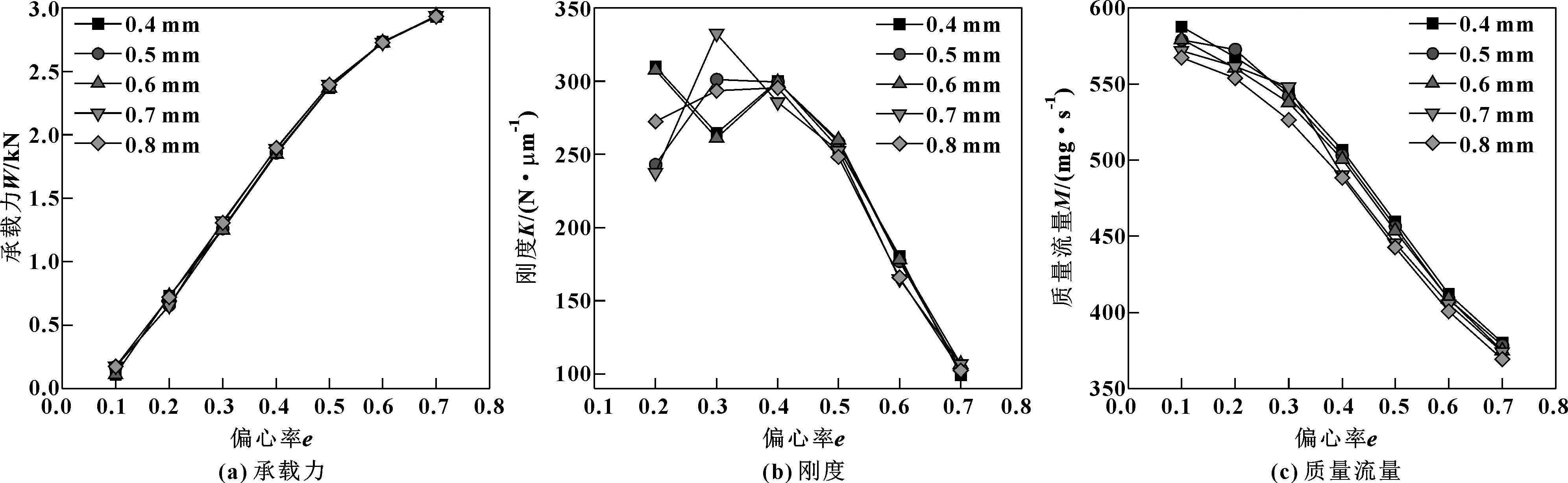
圖11 節流孔高度對軸承承載力、剛度和質量流量的影響

由圖11(a)可知，同一節流孔高度下，隨著偏心率的增大，軸承的承載力不斷提高，且提升速度逐漸變慢；同一偏心率下，不同的節流孔高度對應的承載力沒有明顯區別，說明增加節流孔高度對氣膜壓力沒有明顯影響。

由圖11(b)可知，同一節流孔高度下，隨著偏心率的增大，除l=0.4 mm和l=0.6 mm的軸承剛度在e=0.3時出現波動外，其余高度對應的軸承剛度都是先增大后減小，且剛度的峰值都出現在偏心率較小的情況下；當偏心率e>0.4時，同一偏心率下，節流孔高度越大，對應的軸承剛度越小。

由圖11(c)可知，同一節流孔高度下，隨著偏心率的增大，軸承的氣體質量流量逐漸減小；同一偏心率下，節流孔高度越大，氣體質量流量越小。

綜上所述，增大節流孔高度可以減小耗氣量，但是會減弱軸承的剛度。所以節流孔高度的最佳值為l=0.5 mm。

5.5 節流孔個數對軸承承載性能的影響

在均壓槽深度a=0.2 mm，均壓槽寬度b=0.4 mm,節流孔直徑d=0.2 mm，節流孔高度l=0.5 mm,供氣壓力ps=0.5 MPa的條件下，研究節流孔個數m分別為4、6、8、10、12時對均壓槽復合節流氣體靜壓軸承的承載力W、剛度K和質量流量M的影響。計算結果如圖12所示。

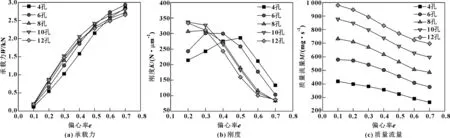
圖12 節流孔個數對軸承承載力、剛度和質量流量的影響

由圖12(a)可知，同一節流孔個數下，隨著偏心率的增大，軸承的承載力不斷提高，且提高速度逐漸變慢；當偏心率e<0.4時，同一偏心率下，孔數越多，對應的軸承承載力越大；當偏心率ε≥0.4時，同一偏心率下，孔數越多，對應的軸承承載力反而越小。這說明當氣膜厚度較大時，增加節流孔個數可以更好地提升軸承的承載力，當氣膜厚度較小時，則相反。

由圖12(b)可知，同一節流孔個數下，隨著偏心率的增大，除m=10和m=12對應的軸承剛度一直減小外，其余孔數對應的剛度先增大后減小；孔數越少，剛度峰值對應的偏心率越小；當e<0.4時，同一偏心率下，孔數越多，其對應的軸承剛度越大，但是當孔數增加到m=12時，其對應的軸承剛度比m=10對應的軸承剛度要小；當e>0.4時，同一偏心率下，孔數越多，其對應的軸承剛度越小。

由圖12(c)可知，同一節流孔個數下，隨著偏心率的增大，軸承的氣體質量流量逐漸減小；同一偏心率下，隨著孔數的增多，氣體質量流量顯著增大。

綜上所述，節流孔個數在偏心率較低時對軸承承載力和剛度的提升效果較為顯著，但增加節流孔個數會導致軸承耗氣量明顯增大，所以節流孔個數的最佳值為m=6。

5.6 供氣壓力對軸承承載性能的影響

在均壓槽深度a=0.2 mm，均壓槽寬度b=0.4 mm,節流孔直徑d=0.2 mm，節流孔高度l=0.5 mm,節流孔個數m=6的情況下，研究供氣壓力ps分別為0.4、0.5、0.6、0.7、0.8 MPa時對均壓槽復合節流氣體靜壓軸承的承載力W、剛度K和質量流量M的影響。計算結果如圖13所示。

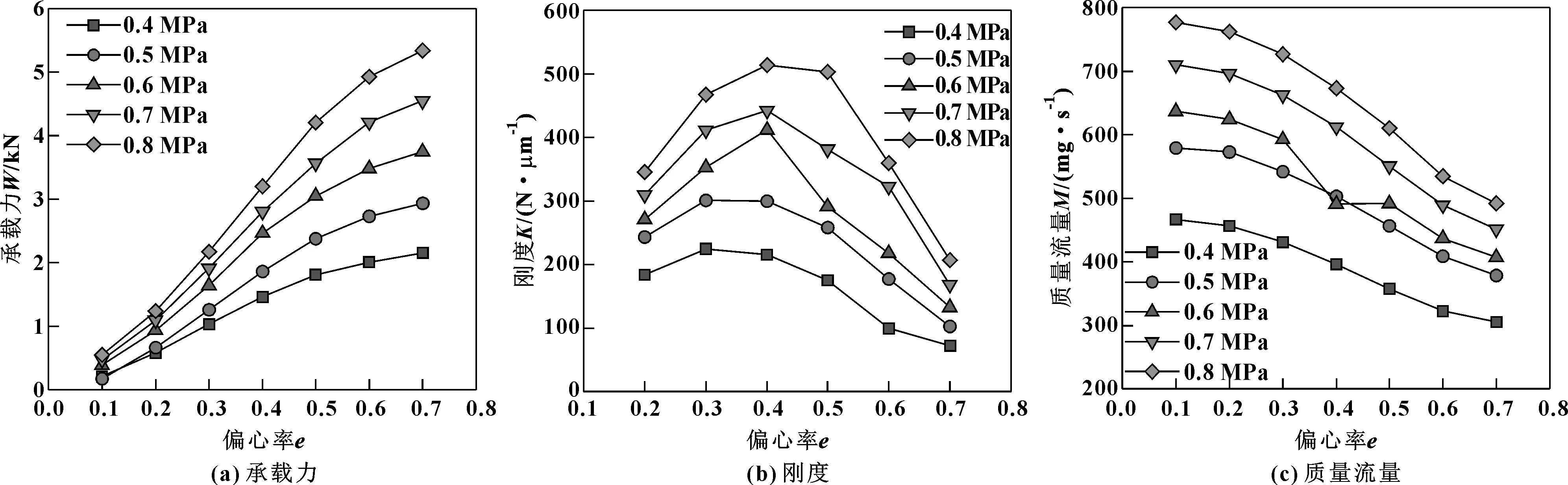
圖13 節流孔高度對軸承承載力、剛度和質量流量的影響

由圖13(a)可知，同一供氣壓力下，隨著偏心率的增大，軸承承載力不斷提高，且提高速度逐漸變慢；偏心率較大時，增加供氣壓力對承載力的提升效果更好；同一偏心率下，供氣壓力越大，其對應的軸承承載力越大。

由圖13(b)可知，同一供氣壓力下，隨著偏心率的增大，軸承剛度先增大后減小，不同的供氣壓力下，軸承剛度都有一個峰值，且供氣壓力較大時，其峰值剛度對應的偏心率也較大；同一偏心率下，供氣壓力越大，對應的軸承剛度也越大。

由圖13(c)可知，同一供氣壓力下，隨著偏心率的增大，軸承的氣體質量流量逐漸減小；同一偏心率下，供氣壓力越大，氣體質量流量越大。

綜上所述，增大供氣壓力雖然可以提高軸承的承載力和剛度，但是也極大地增加了耗氣量。

6 結論

(1)增加均壓槽可以顯著提升氣體靜壓軸承的承載力和剛度。其中，承載力最高提升為之前的6.7倍，剛度最大提升為之前的6.8倍。

(2)隨著軸承偏心率的增大，軸承的承載力逐漸增大，軸承的剛度則先增大后減小，軸承的耗氣量逐漸減小。

(3)增大均壓槽的深度和寬度可以提高軸承承載力，但深度和寬度過大時會降低軸承的剛度；增大軸承的節流孔直徑和個數可以提高軸承的承載力和剛度，但是會增加軸承的耗氣量。

(4) 均壓槽的深度、節流孔的直徑和個數以及供氣壓力對軸承的承載性能影響較大，均壓槽的寬度和節流孔高度對承載性能幾乎沒有影響。