不困于“形”，著力于“理”

周燕

【摘 要】 三年級“除數是一位數的筆算除法”是學習筆算除法的起點。教學中筆者發現，學生在豎式書寫中總是出現類似的錯誤。本文通過對學生在除法計算中出現的典型性錯誤進行分析與思考，探索一些“合理、有效干預”的策略，取得較好效果。

【關鍵詞】 筆算除法? 豎式? 分—換—分? 算理? 數形結合

“除數是一位數的筆算除法”是小學數學中非常重要的內容，在除法計算的學習中起著承上啟下的重要作用。教學實踐中，學生時常出現這樣或那樣的錯例。

對于學生來說，筆算除法書寫格式特別、運算算理特別、算法步驟多，他們在學習的初期往往被繁雜的“形”所困。此外，在學習除數是一位數的除法豎式之前，學生已掌握了表內除法的豎式和整百、整千的數除以一位數的口算（例如 320÷8=40）。這兩類計算都是把被除數當作一個整體，強化了學生一步試商的經驗。在強經驗的刺激下，當學生面對42÷3就會出現同化的“新豎式”（例如）。學生對豎式為什么要由一層變為兩層感到困惑，實質就是不明白除法豎式的來源及意義，再遇到十位除后有剩余的情況，便更加無從下手。因此教學中一定要著力于對每一步計算“理”的探究，充分利用幾何直觀的作用，在抽象的理和法之間搭建一座橋梁。

為了幫助學生克服筆算除法學習中遇到的困難，筆者嘗試在課堂教學中采取“合理、有效干預”的策略，收到較好的教學效果。

教學干預策略一、重組教材，改編例題，調整順序。

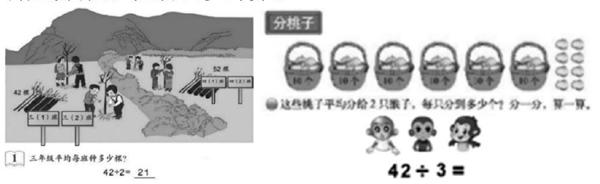
導入新課時將“植樹”主題圖改編為猴兄弟分桃子的情境，接著調整順序，將例題2的“52÷2”改為“42÷3”先于例1前置教學，用黃金時間先解決十位上有余數的情況。這樣的改變有利于學生在后續的分小棒中感受到“分兩次”合理性和必要性，從而自覺接納豎式要分兩步計算。

教學干預策略二、制造“麻煩”，引導探索，明晰算理。

在用42根小棒代替桃子分一分的操作環節，筆者故意提供4張印著一捆小棒的紙片和2根真實的小棒作為學具，給學生制造“分不了”的麻煩，使學生產生用紙片換1捆真實小棒的需求。

【教學片斷】

師：用42 根小棒代替桃子平均分給3只小猴，怎么分？大家都是先分印有整捆小棒的紙片，可是還剩1捆怎么不繼續分下去呢？

生：剩下的這一捆是紙片，分不了！可以用這一張紙片的小棒換一捆真正的小棒嗎？

師：為什么要這樣換呢？

生：一捆真正的小棒可以拆開成10根，這樣就能分下去了。

師：一個“換”字就解決了我們遇到的麻煩，看來學會“換”對我們解決問題很重要。這個分的過程可以概括為“分—換—分”。

教學干預策略三、數形結合，著力建構除法豎式意義。

學生通過分小棒明白了42÷3的算理，接著就用慢鏡頭做“分解動作”，結合操作活動探索豎式寫法，讓“算理”和“算法”慢慢接近。

【教學片斷】

師：你們能把分的過程用豎式的形式記錄下來嗎？怎樣展現出我們剛才的分法呢？

預設學生會出現如下的情況：

師：想一想，小棒一共分了幾次？中途又是怎么換的，通過哪個豎式能看出來？

師：我們把分的過程和第三種豎式結合起來看。先分整捆的，平均分給3只小猴，每只小猴得1捆，也就是1個十，還剩1捆。1寫在什么位置上？為什么？剩下1捆怎么辦？再分單根的小棒，在第一層分行嗎？為什么？那應該寫在哪里？

引導學生通過對比優化自己創造的豎式，把目光聚集到第三種。在邊演示分的過程邊寫豎式、說算理的過程中不斷追問“為什么、怎么辦、應該寫在哪里”，用慢鏡頭做“分解動作”;讓學生明白為什么豎式要寫兩層，為什么十位有剩余時要與個位合并再次分。整個過程以小棒的“形”為支撐，讓學生看之有物，思之有理，也讓“算理”和“算法”完成有效對接。學生鞏固了書寫方法及思考程序，也對豎式的寫法及道理留下深刻的印象。

教學干預策略四、強化對比，變式練習，歸納方法。

1. 嘗試練習：豎式計算42÷2。

2. 觀察比較：42÷3、42÷2的計算過程有什么不同？

3. 寫出42÷6的豎式，對比思考為什么42÷3、42÷2的商是兩位數，而42÷6的商是一位數？

整節課不困于形，著力于理，力求在簡單算理與復雜算法之間架起“分—換—分”的溝通橋梁，利用幾何直觀鋪路搭橋，讓“理”和“法”慢慢接近。“理”明白透了，“法”就順理成章，“講理”與“明法”有機結合，使學生發展能力、增長智慧。

參考文獻

[1] 賈春波，許曉鋁.“錯誤”因干預而美麗——“除數是一位數的筆算除法”錯誤研究及干預策略[J].數學教學通訊，2014，（7）：37-39.

[2] 吳焉.莫讓操作變成擺設——關于一位數除兩位數筆算教學的思考[J].湖南教育，2014（3）：44-45.

[3] 錢聰，以斌.兩位數除以一位數（商是兩位數）的筆算除法課堂教學實錄與評析[J].廣西教育（教育時政），2015（9）：53-56.