聲子晶體結構在功率超聲換能器中的應用*

胡理情 林書玉

(陜西師范大學 陜西省超聲學重點實驗室 西安 710119)

0 引言

夾心式壓電陶瓷換能器，又稱為朗之萬換能器，由于其具有結構簡單、能夠在較低共振頻率下獲得縱向振動等優點，在大功率超聲和水聲領域應用較為廣泛[1]。一般情況下，換能器的振動模式實際是縱向振動與橫向振動的相互耦合，換能器的橫向尺寸應小于其對應特征頻率在陶瓷材料中聲波波長的四分之一，以保證換能器使用一維振動產生的誤差可以忽略不計，此時可以忽略橫向振動。但是隨著換能器的應用范圍的擴大，有兩種情況不可忽略換能器的橫向振動：第一種是當換能器在高頻工作時，相應波長減小，橫向尺寸也需要減小，但是會造成換能器的機械強度下降，為了使換能器工作在高頻，必須增大橫向尺寸，此時尺寸就會大于波長的四分之一，此時換能器的橫向振動不可忽略；第二種是在例如超聲焊接等功率超聲的應用中，需要大功率的超聲，此時需要增大換能器的橫向尺寸[2]。在這兩種情況下，必須對換能器進行優化來抑制耦合振動對換能器的影響。林書玉等[3]、梁召峰等[4]通過焊接頭開槽來改進超聲焊接系統，基本上解決了換能器的耦合振動問題，但是并沒有用理論來解釋開槽如何對振動進行影響。隨著聲子晶體結構帶隙理論的出現，越來越多的學者將其應用于減振降噪方面，而這種周期性的開槽結構就類似于聲子晶體的周期型結構排列。由聲子晶體的定義可知，它是由密度和彈性常數不同的兩種材料按周期性結構復合在一起形成，圖1(a)是一個二維聲子晶體結構，互不連通的材料稱為散射體，連通為一體的材料稱為基體[5]，圖1(b)為聲子晶體原胞的截面圖，其中圓形為散射體，其余為基體，a為原胞的晶格常數，r為散射體的半徑。聲子晶體結構形成的特殊色散關系，會使得處于帶隙范圍內的彈性波被禁止傳播。將開槽后的結構定義為一個聲子晶體結構，空氣為散射體，剩余材料為基體，由此可以解釋對橫向振動的抑制作用是由于共振頻率處于聲子晶體帶隙范圍內，被禁止傳播。由圖1(a)可以看出，二維聲子晶體結構與1-3型復合材料結構相似，Wilm等[6]將1-3 型復合材料對橫向振動的抑制作用從聲子晶體理論角度進行解釋，采用平面波展開法，在考慮了壓電效應、聲損失和電激勵條件下，得到了色散關系；為了將材料應用于超聲成像，Wilm 等[7]得到了非零的角度入射時的帶隙圖；Aragón 等[8]和Ronda等[9]也研究了帶有壓電效應的聲子晶體，在壓電陶瓷片的厚度方向周期性地開圓形孔陣列來抑制橫向振動，說明有限周期的圓柱形孔的聲子晶體在對耦合振動的抑制有明顯的效果。但是由于壓電陶瓷片脆性大，對其開孔難度較大，本文選擇在前蓋板上開周期結構圓柱形孔。換能器的前蓋板作用是為了將換能器產生的能量沿著縱向高效地輻射出去，輻射面位移分布越均勻，輻射阻抗越大，能夠有效提高換能器的輻射功率，將前蓋板設計成聲子晶體結構，調整尺寸使共振頻率處于帶隙內，從而達到抑制橫向振動的目的。Khelif 等[10]研究了在聲子晶體中聲波的傳播問題，除散射體的填充率外，完全帶隙是否存在以及帶隙的寬度與聲子晶體的厚度與晶格周期的比值也有關系；王莎等[11]在喇叭形前蓋板上沿半徑方向開周期性槽，調整開槽高度和寬度來達到抑制橫向振動的目的，這是一種類聲子晶體結構模型，可以得知散射體的高度和大小對聲子晶體的帶隙特性存在很大的影響。

圖1 二維聲子晶體及原胞截面圖Fig.1 Cross section of two-dimensional phononic crystal and primitive cell

色散曲線圖能夠直觀地了解聲子晶體的帶隙特性，平面波展開法是求解聲子晶體色散曲線最常用的方法之一。理想的二維聲子晶體在兩個維度是無限周期的，不考慮厚度的影響，采用平面波展開法可以計算出它的能帶結構，但是功率超聲換能器的結構是有限大小的，基于聲子晶體結構的前蓋板只能是有限周期結構，要使得聲子晶體應用于功率超聲換能器中，需要計算出有限周期結構的聲子晶體的傳輸特性[12]。本文采用有限元法仿真了二維聲子晶體前蓋板的傳輸特性，將共振頻率設計在帶隙范圍內，通過對不同高度和半徑的散射體帶隙進行計算并結合共振頻率分析，找到前蓋板的最佳尺寸，使其最大程度地對橫向振動進行抑制，明顯降低徑向振動位移，輻射面位移分布也更加均勻。

1 基于二維聲子晶體結構的前蓋板對換能器共振頻率的影響

傳統的夾心式換能器由等截面的圓柱形前后蓋板和壓電陶瓷片組成，陶瓷片的極化沿厚度方向，如圖2(a)所示的傳統的夾心式換能器，中間是由兩塊陶瓷片組成，極化方向相反，整個振子的厚度等于基波的半波長，橫向尺寸遠小于縱向長度，滿足一維振動理論。但是受實際應用的影響，換能器的橫向尺寸相對較大時，產生強烈的耦合振動會導致換能器的效率下降，因此，本文設計了一種具有基于二維聲子晶體結構前蓋板的功率超聲換能器，模型如圖2(b)所示，換能器的共振頻率在20 kHz 附近，前后蓋板高度為56 mm，整體的截面半徑R為26 mm，壓電陶瓷片的厚度為6 mm，在前蓋板的前端沿縱向開圓柱形孔，形成近周期構開孔結構，即聲子晶體結構。前蓋板開孔后的截面如圖2(c)所示，黑色正方形為聲子晶體的一個原胞，在x和y方向為近周期性結構，晶格常數a為10 mm，散射體半徑為r。

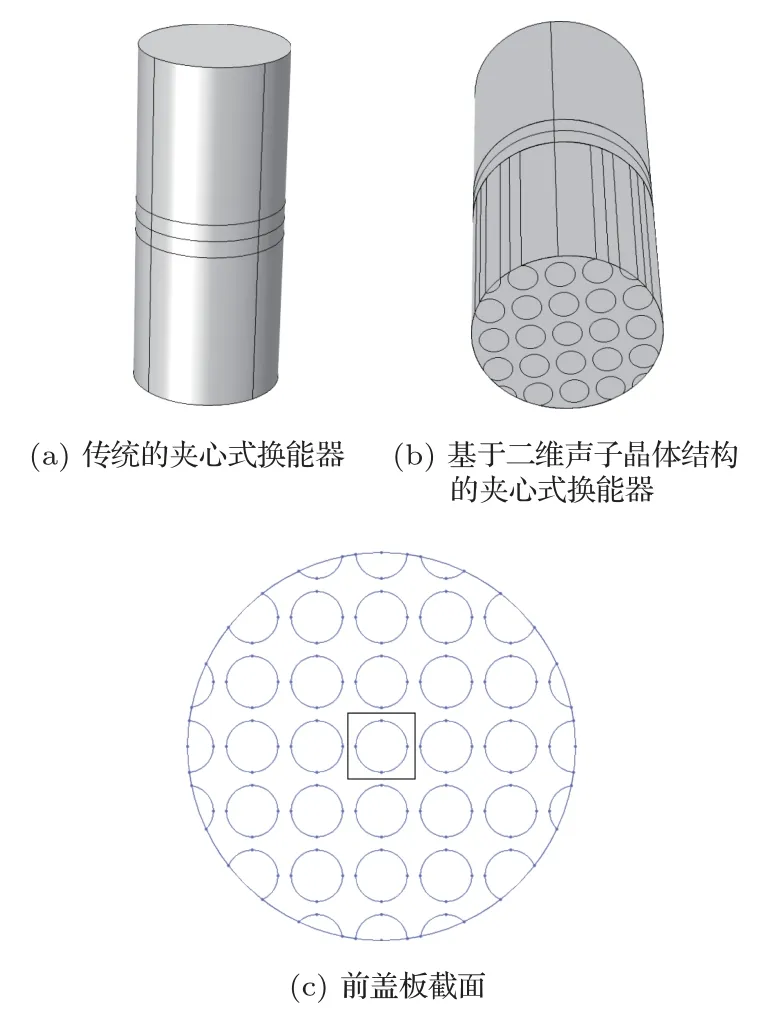
圖2 傳統的夾心式換能器模型和基于二維聲子晶體結構的夾心式換能器模型Fig.2 Traditional sandwich transducer model and sandwiched transducer based on two-dimensional phononic crystal structure model

通過有限元法研究散射體的大小對換能器的縱向共振頻率的影響，在靜電場和固體力學兩個物理場中進行研究，建立換能器的幾何模型如圖2所示，前蓋板和后蓋板的材料定義為鋁，兩個壓電陶瓷片的材料為PZT-4，為了簡化模型，本文暫不考慮預應力螺栓對換能器振動特性的影響。通過對特征頻率求解得出模型的縱向共振頻率，圖3(a)是仿真得到的傳統夾心式換能器的振型圖，可知不開孔時換能器的縱向共振頻率為19.871 kHz。將模型前蓋板改為聲子晶體結構，基體為鋁，散射體是空氣，圖3(b)是散射體半徑為4 mm 時換能器的振型圖，得到的縱向共振頻率為20.396 kHz，可知散射體的半徑對換能器的共振頻率存在影響。本文進一步通過改變散射體的半徑或者高度對換能器的特征頻率進行研究。

圖3 傳統的夾心式換能器和基于二維聲子晶體結構前蓋板的換能器的振型圖Fig.3 The vibration pattern diagram of traditional sandwich transducer and the transducer based on the front cover plate with twodimensional phonon crystal structure

保持其他結構參數不變，改變聲子晶體結構前蓋板的散射體半徑。分別在有限元軟件中建立散射體半徑為3.7 mm、3.8 mm、3.9 mm、4.0 mm、4.1 mm、4.2 mm、4.3 mm、4.4 mm、4.5 mm 的換能器模型，對模型的特征頻率進行研究，得到縱向共振頻率分別為20.288 kHz、20.322 kHz、20.358 kHz、20.396 kHz、20.441 kHz、20.488 kHz、20.533 kHz、20.586 kHz、20.638 kHz，關系圖如圖4(a)所示，可知隨著前蓋板散射體半徑的增大，換能器的縱向共振頻率也在逐漸增加。同樣的保持其他結構參數不變，將散射體半徑固定為4 mm，通過改變散射體的高度來觀察功能共振頻率的變化，建立散射體高度分別為0 mm、7 mm、14 mm、21 mm、28 mm、35 mm、42 mm、49 mm、56 mm 的模型，縱向共振頻率分別為19.871 kHz、18.502 kHz、17.861 kHz、17.468 kHz、17.324 kHz、17.525 kHz、18.060 kHz、19.021 kHz、20.396 kHz，關系圖如圖4(b)所示，可知隨著前蓋板散射體高度的增加，共振頻率先減小后增大。研究表明，前蓋板散射體的大小對換能器的振動特性影響存在規律性，換能器的共振頻率可以通過散射體進行調節，結合聲子晶體結構前蓋板的帶隙范圍設計夾心式換能器，能找到聲子晶體結構前蓋板的最佳尺寸，使得橫向振動得到最好的抑制。

圖4 夾心式換能器的共振頻率Fig.4 Resonant frequency of sandwich transducers

2 二維聲子晶體結構前蓋板帶隙的研究

2.1 散射體半徑和高度對帶隙的影響

近年來有不少學者對換能器耦合振動的抑制進行了研究，將超聲塑料焊接系統的工具頭開周期性結構的槽，有效實現了焊接系統的優化[13-14]，表明聲子晶體的帶隙特性對于橫向振動的抑制確實存在很好的效果。對于縱向振動的夾心式換能器，也需避免與其他模式的振動耦合，造成換能器的效率低下。聲子晶體結構對頻率處于帶隙范圍內的振動才會具有抑制作用，可以確定二維聲子晶體結構前蓋板是否存在帶隙以及依據存在帶隙的范圍來考慮是否對換能器的耦合振動存在抑制。聲子晶體結構前蓋板是有限周期結構，采用有限元仿真對其帶隙進行研究。首先研究散射體的半徑對聲子晶體結構前蓋板帶隙的影響，在前蓋板開周期性結構的孔，改變孔的半徑大小。對于聲子晶體結構的研究在有限元軟件的固體力學模塊中進行，將模型沿徑向施加1 m/s2加速度幅值，使得彈性波在二維聲子晶體結構前蓋板中傳播，在對應的另一側進行計算，得出模型的加速度響應曲線，將加速度幅值小于1 m/s2時的頻率范圍定義為求解模型的帶隙。帶隙研究的模型為前蓋板，高度為56 mm，改變散射體半徑，分別建立散射體半徑為3.8 mm、4.0 mm、4.2 mm、4.4 mm 的4 個模型；保持散射體半徑為4 mm，改變散射體高度，分別建立散射體高度為56 mm、49 mm、42 mm、35 mm、28 mm的5個模型。對所建立的模型的頻域進行研究得到的加速度響應曲線的結果，如圖5所示。

從圖5(a)可以看出，在換能器的設計共振頻率20 kHz 附近不同散射體半徑的散射體帶隙存在情況不一樣，并且散射體的半徑對聲子晶體前蓋板的帶隙存在很大的影響，由圖中的4 個不同散射體半徑時的加速度響應曲線可知，當散射體半徑為3.8 mm 時，帶隙范圍是17.0～25.4 kHz；當散射體半徑為4.0 mm 時，帶隙范圍是15.7～23.1 kHz；當散射體半徑為4.2 mm 時，帶隙范圍是14.4～21.0 kHz；當散射體半徑為4.4 mm 時，帶隙范圍是17.0～25.4 kHz。帶隙范圍的大小隨著散射體半徑的增大而減小，并且向高頻方向移動。結合模型的共振頻率進行分析，散射體半徑為4 mm 時的共振頻率對應的加速度幅值的衰減是最大的，此時的減振效果是最好的。再對散射體高度對帶隙的影響進行分析，圖5(b)是保持散射體半徑為4 mm、改變散射體高度時，計算得到的加速度響應曲線，從圖中可以看到隨著散射體高度的增加，帶隙向低頻方向移動，而共振頻率隨著散射體高度先減后增，很明顯可以得到散射體高度為56 mm 時的共振頻率對應的加速度幅值的衰減是最大的。綜合以上仿真所得到的結果進行分析，可以得知此換能器能夠有效抑制橫向振動時前蓋板最佳尺寸是散射體半徑為4 mm、高度為56 mm，此時共振頻率處在帶隙范圍內并且加速度幅值的衰減強度接近最大值，對換能器的耦合振動抑制效果最好。

圖5 加速度響應曲線Fig.5 Acceleration response curve

2.2 聲子晶體結構前蓋板對換能器振動特性的影響

利用有限元的方法基于聲子晶體帶隙理論對前蓋板開孔結構的橫向振動抑制作用進行了分析，得到了具有聲子晶體結構前蓋板的換能器的最佳設計尺寸，本文接著對徑向位移進行計算，研究其對換能器橫向振動的抑制效果。將換能器的振型圖通過有限元仿真出后，對換能器前蓋板側面沿著正對著模型的y軸方向從上至下取截線距離為0～56 mm，如圖6所示。定義取截線的方向為y方向，通過有限元分析計算得出換能器在徑向的相對位移如圖7所示，紅色虛線為傳統夾心式的徑向位移，黑色實線為具有聲子晶體結構前蓋板的換能器的徑向位移，徑向位移在前蓋板開周期性結構孔徑后明顯變小，表明聲子晶體結構前蓋板對換能器的橫向振動存在明顯抑制效果。本文還對換能器的前蓋板輻射面的位移進行計算，研究換能器位移分布的均勻性。同樣采取對前蓋板前端的輻射面取截線對其縱向位移進行計算，前蓋板未開孔時縱向振動最大位移與最小位移的之差為0.19 μm，采用聲子晶體結構前蓋板后縱向振動最大位移與最小位移的之差為減小為0.12 μm，說明此時換能器的位移分布更加均勻，輻射面的位移分布越均勻，輻射阻抗越大，從而輻射功率增大，提升了換能器的性能。

圖6 前蓋板側向截線示意圖Fig.6 Diagram of longitudinal transversal of front cover plate

圖7 換能器的徑向位移Fig.7 The radial displacement of the transducer

3 結論

本文基于聲子晶體的帶隙理論，對夾心式換能器進行優化。在傳統夾心式換能器基礎上，通過將換能器的前蓋板加工成二維聲子晶體結構，使得共振頻率處于二維聲子晶體結構前蓋板的帶隙范圍內，從而達到抑制換能器橫向振動的目的。這種結構的縱向振動的夾心式換能器的振動模態更加的單純，對換能器的振動特性有明顯的優化。本文討論了散射體的半徑大小及高度對換能器的共振頻率、聲子晶體結構前蓋板帶隙以及換能器的振動特性的影響，得出了如下結論：

(1)二維聲子晶體結構前蓋板對換能器的共振頻率存在影響，隨著散射體半徑的增大，共振頻率也在變大，隨著散射體高度的增加，共振頻率先增加后減小；

(2)通過有限元仿真法計算的加速度響應曲線可知二維聲子晶體結構前蓋板存在包含換能器共振頻率的帶隙范圍，并且帶隙的范圍會隨著散射體的半徑和高度發生變化；

(3)在換能器前蓋板前端開圓柱形孔徑形成的二維聲子晶體結構能夠有效抑制大尺寸夾心式換能器的橫向振動，優化換能器的振動性能。

大尺寸夾心式換能器的耦合振動是在橫向尺寸過大時會出現的一種現象，對換能器的工作效率會造成很大的影響，本文基于二維聲子晶體結構帶隙的有限元法研究為抑制功率超聲換能器的耦合振動提供了一種新的方案，在實際應用中具有重要意義。