風速對通電線圈溫度影響的多參數CFD模擬

孟群曜 蘆俊杰 王佳輝 高宇辰 劉永露

摘? 要：風流過一個通有電流的導體線圈，線圈的溫度會降低。利用CFD計算技術，對由風速、線圈材料、線圈熱功率等參數引起的溫度變化進行了研究。在風速為1 m·s-1～50 m·s-1范圍內，采用標準k-ε湍流模型，對通電線圈周圍的熱流場進行了數值模擬。結果表明：隨著風速增大，線圈溫度降低;隨著線圈產熱功率增加，線圈溫度隨之升高;線圈尺寸增大，溫度升高;線圈材質對線圈溫度沒有影響。

關鍵詞：風速;載流線圈;CFD

中圖分類號：TJ206 ? ? ?文獻標識碼：A 文章編號：2096-4706（2021）02-0135-04

Abstract：When air flows through a conductor coil with current，the temperature of the coil will decrease. The temperature changes caused by the following parameters，such as wind speed，coil material，coil thermal power etc are studied by using CFD calculation technology. In the wind speed range of 1 m·s-1～50 m·s-1，the standard k-ε turbulence model is used to make numerical simulation on the heat flow field around the current coil. The results show that the coil temperature decreases with the increase of wind speed，the coil temperature increases with the increase of coil thermogenic power，the coil temperature increases with the increase of coil size，and the coil material does not affect the coil temperature.

Keywords：wind speed;current-carrying coil;CFD

0? 引? 言

熱線風速儀由于檢測元件小，熱慣性小，靈敏度及空間分辨力高，對流態干擾小，能用于測量動態隨機變量，是目前分析流體內部時空變化方面最為合適的量測儀器之一[1]。King提出了無限長線和流體之間的熱對流理論[2]促使熱線探頭技術發展。這一理論是開發一些測控儀器，如熱線風速儀等儀器的基本原理。探究并明確風速對線圈溫度影響規律是開發這些測控儀器和設備的必要前提。在熱線風速儀的設計與應用中，最為棘手的問題是流體的湍流對儀器測量精度的影響[3]。本文利用計算流體動力學（Computational Fluid Dynamics，CFD）技術，同時主要關注線圈的溫度及周圍傳熱情況，對湍流流體空氣流經通電線圈這一過程進行模擬分析，為該過程提供了參考數據，有利于提高熱線風速儀儀器的精度。CFD是近年來廣泛應用的研究流體流動與傳熱的方法之一。國內外很多學者利用CFD相關理論知識[4，5]，對傳熱線圈進行了深入的研究和分析。白云峰等[6]、張月紅等[7]和吳坤等[8]采用數值模擬方法研究了線圈位置、感應加熱系統精度等參數對溫度場的影響;依據現有的研究結果，林志偉等[9]對恒功率式熱膜風速計進行了設計。

CFD是通過計算機數值模擬求解流體力學控制方程，對流體流動等現象進行數值分析、研究和預測的學科[10]。

基于傳熱原理的理論分析可以得出風速與功率，溫度差的關系滿足：

式中：P為加熱功率;I為加熱電流;R為加熱電阻;Tw為線圈表面溫度;Tf是環境溫度探頭測得溫度;A和B是與線圈材料和結構相關的常數;u為氣體流速值。

由式（1）可以得出在導熱功率恒定的情況下，線圈的溫度差與氣體的流速應該滿足二次函數關系。本文利用計算流體動力學軟件，研究了不同流速下，線圈加熱功率、尺寸和材料對線圈溫差的影響，探究二者在不同條件下的相關系數及估計標準誤差。

1? 模型及模擬方法

1.1? 模型的建立

空氣流通的通道為一正方體，圓環型線圈位于正方體中心。正方體流域的長寬高均為100 mm，線圈直徑Ф=1 mm，1號圓環半徑為R1=5 mm;2號圓環半徑為R2=15 mm。通過改變進口風速、線圈尺寸及產熱功率來計算不同參數下線圈的溫度。計算模型如圖1所示。

1.2? 網格劃分及網格獨立性驗證

采用正四面體非結構化網格對內置線圈的正方體流道進行了網格劃分，為準確計算線圈附近的溫度值，對線圈周圍進行了網格加密處理。流道及線圈處網格如圖2和圖3所示。對通道網格整體的質量進行了檢驗，得到的網格質量值直方圖如圖4所示。由圖4可見，網格質量大部分高于0.43，可認為網格質量良好。

為驗證網格的獨立性，排除網格的疏密程度對解的影響，對近線圈處進行了不同的加密處理，得到了5套節點數不同的網格。采用不同網格節點數目對線圈溫度計算結果的影響如圖5所示。由圖5可見，當網格數量接近15萬時，計算結果已與網格數量無關。綜合考慮精度要求和計算資源，本文采用圖中節點數為21萬的網格進行計算。

1.3? 控制方程及邊界條件

本文采用標準k-ε湍流模型對內置產熱線圈的正方體通道內的流體流動和傳熱進行了計算。穩態運行時的連續性方程、動量和能量守恒方程如式（2）～（8）所示。

式中：Gk為平均速度梯度引起的湍動能;Gb為浮力影響產生的湍動能;YM為可壓縮湍流脈動膨脹對總耗散率影響的貢獻;C1s、C2s、Cμ為常數。控制方程的邊界條件及參數設定值如表1所示。采用速度和壓力耦合求解方法，連續性方程、動量方程和能量方程的收斂條件為10-3、10-4和10-6，以空氣為研究介質，改變入口速度計算不同條件下線圈的溫度。

2? 參數對線圈溫度的影響

應用上述模型和計算方法，得到了如圖6所示的流場溫度等值線圖，研究了風速、線圈尺寸及產熱功率等多因素對線圈溫度的影響。從圖6可知，線圈溫度遠高于空氣的溫度，這是由于線圈內部有熱量產生的緣故。線圈表面溫度低于線圈內部溫度，這是由于線圈表面有大量冷空氣流動，線圈與冷空氣之間進行的傳導和對流傳熱降低了線圈的表面溫度。

2.1? 風速對線圈溫度的影響

采用鋁材質的線圈，在線圈直徑為1 mm，圓環半徑為5 mm，線圈產熱功率P=1.0×107 W·m-3條件下，風速為1 m·s-1、5 m·s-1、10 m·s-1、20 m·s-1、30 m·s-1、40 m·s-1、50 m·s-1時，線圈的溫度分別為376.0 K、347.6 K、338.8 K、332.9 K、329.0 K、325.5 K和322.7 K。以風速的平方根為橫坐標，以線圈溫度與空氣溫度差值的倒數為縱坐標，可得到如圖7所示的線圈溫度隨風速的變化規律圖。

從數據和圖7可以看出，隨著風速的提高，線圈溫度降低，這是由于隨著風速增大，線圈與空氣之間的對流傳熱系數增大，單位之間傳遞的熱量增多，因此在線圈加熱功率恒定的條件下，風速越大，線圈表面溫度就越低。從圖7可以看出，風速的平方根與線圈溫度和空氣溫度差值的倒數呈現一定的線性關系。利用線性回歸可計算得到斜率b=0.004 8，截距a=0.009 4，相關系數η=0.991 5，說明二者線性相關。截距和斜率可用于計算式（1）中的常數。

2.2? 線圈產熱功率對線圈溫度的影響

在線圈直徑為1 mm，圓環半徑為5 mm條件下，考察了線圈產熱功率對線圈溫度的影響。當線圈產熱功率為P=1.5×107 W·m-3時，風速為1 m·s-1、5 m·s-1、10 m·s-1、20 m·s-1、30 m·s-1、40 m·s-1、50 m·s-1對應的線圈溫度分別為420.1 K、367.0 K、356.7 K、349.3 K、343.6 K、338.3 K和334.1 K。產熱功率對線圈溫度的影響如圖8所示。

參照2.1節中線圈產熱功率P=1.0×107 W·m-3時線圈的溫度，對比不同產熱功率下線圈溫度可知，相同氣體流速時，線圈產熱功率越大，其表面溫度越高。這是由于當氣體流速恒定時，線圈與空氣之間的對流傳熱系數基本為一常數，由傅里葉傳熱公式Q=KAΔTm可知，當傳熱系數K和傳熱面積A一定時，增大傳熱量Q，傳熱溫差會變大。因此當線圈產熱功率變大時，線圈表面溫度會升高。

利用線性回歸計算出P=1.5×107 W·m-3時趨勢線的斜率和截距，得斜率b=0.003 2，截距a=0.006 2，相關系數η=0.986 9。

由公式（1）可知，與線圈結構和材料相關的兩個參數A和B分別正比于a×P，b×P，對不同產熱功率下得到的數據進行整理，可得到如表2所示的對比結果。

由表2可見，本文所采用的兩種功率下，b×P的值相同，a×P的值偏差為1%。說明本文模擬所取得的數據結果均符合理論公式，結果可靠。

2.3? 線圈尺寸對線圈溫度的影響

在線圈直徑為1 mm，產熱功率P=1.0×107 W·m-3時，考察了不同圓環半徑對線圈溫度的影響。當圓環半徑R=15 mm時，風速為1 m·s-1、5 m·s-1、10 m·s-1、20 m·s-1、30 m·s-1、 40 m·s-1、50 m·s-1對應的線圈溫度分別為661.1 K、453.9 K、413.1 K、373.4 K、356.5 K、346.6 K和340.2 K。結果如圖9所示。

參照2.1節中R=5 mm時線圈的溫度，對比不同產熱功率下線圈溫度可知，相同氣體流速時，圓環半徑越大，其表面溫度越高。這是因為圓環半徑增大，線圈產熱功率增大，線圈產熱功率與體積成正比，即Q與R成正比。雖然圓環半徑增大，傳熱面積也增大，然而線圈與空氣之間的傳熱面積A與R成正比。當風速一定時，線圈與空氣之間的對流傳熱系數基本一定，因此由傅里葉傳熱公式可知，增大圓環半徑，線圈溫度增大。

利用線性回歸計算出圖9中趨勢線的斜率和截距，得斜率b=0.003 6，a=-0.001 8，相關系數R=0.991 3。

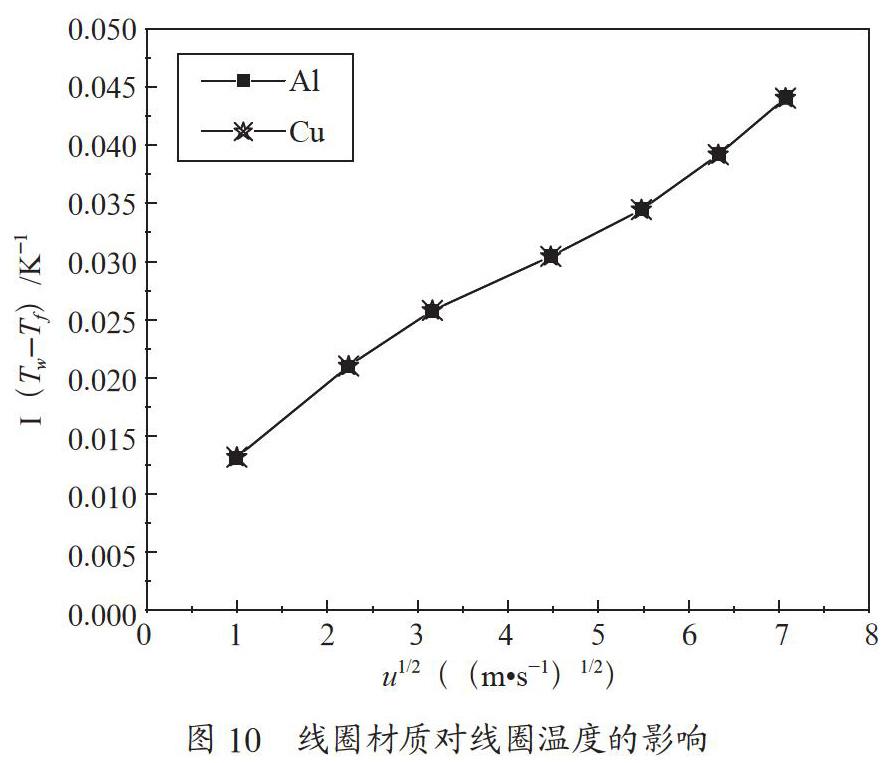
2.4? 線圈材質對線圈溫度的影響

在線圈直徑為1 mm，圓環半徑R=5 mm，產熱功率P= 1.0×107 W·m-3時，考察了不同材質對線圈溫度的影響，結果如圖10所示。

由圖10可見，當產熱功率和線圈尺寸相同時，線圈的材質對線圈溫度幾乎沒有影響。這是因為盡管線圈材質不同，其導熱系數差異較大，然而，在本文所研究的氣速范圍內，線圈與空氣之間的傳熱主要由對流方式進行，而由傳導方式傳遞的熱量微乎其微。因此，盡管采用不同導熱系數的材質進行模擬實驗，在產熱功率和線圈尺寸相同時，不同材質的線圈溫度不會呈現出明顯的差異。

3? 結? 論

本文采用CFD軟件對正方形通道內風作用下的線圈溫度進行了模擬計算，考察了風速、線圈產熱功率、線圈尺寸和材質等多因素對線圈溫度的影響。取得以下結論：

（1）利用數值模擬方法取得的線圈溫度與空氣溫度差值的倒數與風速的平方根線性相關系數大于0.99;不同條件下得到的與線圈結構和材料相關的常數的偏差為1%;說明模擬結果可靠，所取得的數據可用于開發和設計與風作用下載流線圈溫度變化相關的儀器設備。

（2）其他條件不變的情況下，增大風速，線圈溫度降低;增大線圈產熱速率，線圈溫度升高;增大線圈尺寸，線圈溫度升高;線圈材質對其溫度幾乎無影響。

參考文獻：

[1] 劉祖唐，沈懋如.熱線風速儀 [J].河海大學學報（自然科學版），1982（3）：133-142.

[2] KING L V.On the Convection of Heat from Small Cylinders in a Stream of Fluid：Determination of the Convection Constants of Small Platinum Wires with Applications to Hot—Aire Anemometry [J].Philosophical Transactions of the Royal Society of London，1914，214（509-522）：373-432.

[3] 韋青燕，張天宏.高超聲速熱線/熱膜風速儀研究綜述及分析 [J].測試技術學報，2012，26（2）：142-149.

[4] 王福軍.計算流體動力學分析：CFD軟件原理與應用 [M].北京：清華大學出版社，2004.

[5] 韓占忠，王敬，蘭小平.FLUENT：流體工程仿真計算實例與應用 [M].北京：北京理工大學出版社，2004.

[6] 白云峰.線圈接線位置對管坯感應加熱溫度場影響的數值模擬 [J].寶鋼技術，2011（4）：23-26.

[7] 張月紅.感應加熱溫度場的實驗與仿真研究 [J].企業科技與發展，2010（4）：44-46.

[8] 吳坤.基于ANSYS的感應加熱系統高精度仿真研究 [D].杭州：杭州電子科技大學，2014.

[9] 林志偉.恒功率式熱膜風速計設計 [D].哈爾濱：哈爾濱理工大學，2014.

[10] 楊昂，張濤，盧學強，等.計算流體力學技術在膜分離過程中的應用與進展 [J].城市環境與城市生態，2013，26（6）：20-23.

作者簡介：孟群曜（2001—），男，滿族，遼寧沈陽人，本科在讀，研究方向：自動化;劉永露（1989—），男，漢族，重慶人，系副主任，副教授，博士，研究方向：電氣控制。