超臨界二氧化碳溶脹天然橡膠動力學分析*

宋 琪，王貝貝，夏浩海，王曉冰，李 翔，鄧曉清**

(1．長江大學 化工與環境工程學院，湖北 荊州 434023；2．長江大學 機械工程學院，湖北 荊州 434023)

超臨界二氧化碳(ScCO2)是一種新型綠色溶劑，在化工生產過程中受到越來越多的關注。它既具有液體的溶解性，又具有氣體的滲透性，廣泛應用于萃取分離、有機物合成、廢棄物降解、新染色工藝開發、材料發泡和微粒制備以及干燥與清潔等領域[1-6]。相比于傳統溶劑，ScCO2具有諸多優勢，如價格低廉、環境友好、不易燃易爆、環境狀態下易與高分子材料分離等[7]。

在高分子材料領域，ScCO2通常作為反應溶劑或者增塑劑，應用過程中包括大分子或者小分子的質量傳遞[8]。ScCO2和高分子材料形成的兩相體系中，二氧化碳分子向高分子材料內部擴散，產生溶脹現象，溶脹的高分子鏈段空間構型發生變化，其物理特性也會相應地發生變化[9]。因此，有必要分析ScCO2在高分子材料中的擴散和高分子材料的溶脹過程。

溶脹最顯著的特點是材料表觀尺寸的變化，可以通過直接觀測的方法分析高聚物吸收以及解吸溶劑的過程[10]。溶脹動力學就是溶劑吸附量隨時間的變化，是一個擴散過程。對于玻璃化轉變溫度以上的高聚物，溶劑分子的擴散速率小于交聯網絡大分子鏈的松弛速率，為Fickian溶脹過程。對于玻璃化轉變溫度以下的高聚物，聚合物鏈的松弛速率緩慢，溶劑分子的擴散速率更快，為non-Fickian溶脹過程[11]。溶劑在玻璃態高聚物中的擴散可以觀察到明顯的擴散前沿，直觀地分析溶劑的擴散距離，通過Fick定律確定擴散系數[12]936-938。而對于玻璃化轉變溫度以上的高聚物，溶劑的擴散過程中只能觀察到樣品尺寸的整體變化。Crack基于Fick第二擴散定律，推導了矩形、球形以及展開平面的擴散方程[13]40，據此可以計算高彈態高聚物中的溶劑擴散。

一些學者研究了ScCO2在高分子材料中的擴散過程，Lemert等[14]研究了聚異戊二烯橡膠在ScCO2中的溶脹過程，樣品為非硫化橡膠，沒有觀察到詳細的尺寸變化。Kojima等[15]178-181在此基礎上分析了球狀硫化的聚異戊二烯橡膠的溶脹過程，觀察了溶脹尺寸的變化。辛曉等[16]也采用同樣的方法分析了圓柱狀硫化天然橡膠在ScCO2中的溶脹過程。通過以上方法可以得到ScCO2在橡膠高分子中的擴散系數，但是均沒有詳細分析交聯密度以及溶脹溫度、壓力等因素對于擴散的影響規律，并且沒有從動力學角度分析擴散過程。有鑒于此，本文制備了不同交聯密度的天然橡膠樣品，通過溶脹動力學分析了不同溫度下ScCO2在橡膠高分子中的擴散過程。

1 實驗部分

1.1 原料

天然橡膠：云標1#，云南南泰橡膠有限公司；硫磺：分析純，阿拉丁試劑(上海)有限公司；氧化鋅、硬脂酸、促進劑CZ：分析純，阿拉丁試劑；甲苯：硫化橡膠交聯密度測量溶劑，分析純，國藥集團化學試劑有限公司；二氧化碳：分析純，武漢紐瑞德特種氣體有限公司。

1.2 儀器及設備

高溫高壓可視反應釜：UF-200-30，江蘇聯友科研儀器有限公司。材料為316 L，設計溫度200 ℃，設計壓力為30 MPa。CCD相機：istav DH 734-18F-03,Andsr實驗設備簡圖如圖1所示。

圖1 可視窗反應釜簡圖

1.3 實驗方法及過程

實驗過程中，首先將膠球懸空置于高壓反應釜中部，關閉反應釜蓋，二氧化碳由柱塞泵輸入反應釜內，通過多次置換以除去反應釜內空氣，之后將反應釜加壓到預設壓力。加熱裝置為電加熱爐，升溫速率為3 ℃/min，隨著溫度的升高，壓力逐漸增大，到達目標溫度所對應的壓力即為目標壓力。溫度和壓力測量傳感器精度分別為-0.1～0.1 MPa。反應釜兩側有石英玻璃可視窗，由于溶脹作用膠球在ScCO2中體積逐漸變大，通過連續拍攝膠球體積增大過程，進而采用圖形軟件分析膠球的溶脹程度。

1.4 硫化橡膠樣品的制備

制備不同交聯密度的橡膠球，具體配方如表1所示(按質量份計)，為了便于分析采用最簡化的配方，不含任何油和填料。橡膠球初始半徑為7 mm，膠球交聯密度根據Florye-Rehner方程計算[17]。樣品A和B的交聯密度分別為0.78×10-4mol/cm3和1.9×10-4mol/cm3。

表1 天然橡膠混煉膠組成

2 溶脹動力學分析

溶脹動力學研究橡膠在溶劑中的溶脹速率，也就是膠球表觀體積變化速率，時間t時刻溶脹率St表達式如式(1)。

(1)

式中：V0為(目標溫度下)未溶脹橡膠體積，mm3；Vt為溶脹t時刻后橡膠的體積增量，mm3；r0為(目標溫度下)未溶脹橡膠半徑，mm；rt為(目標溫度下)溶脹t時刻后橡膠的半徑，mm。通過對溶脹度進行擬合，分析適合溶脹過程的經驗方程。

2.1 溶脹動力學方程

分析溶脹速率變化符合一階或二階動力學過程，一階動力學方程如式(2)所示。

(2)

式中：S是時間t時刻的溶脹率，Se是溶脹達到平衡時的溶脹率，K1是一階溶脹動力學常數，由溶脹速率和dS/dt和剩余溶脹能力Se-S的比例求得。式(2)積分可得方程式(3)。

(3)

ScCO2中膠球溶脹二階動力學方程如式(4)所示。

(4)

從時間0到t積分式(4)得到式(5)。

(5)

K2是二階動力學常數，K2減小溶脹過程變慢。二階動力學方程系數由式(5)較難直接獲得，可擬合回歸方程快速求得，如式(6)所示，由截距b1即可求得K2。

(6)

擬合系數b0和b1如式(7)、式(8)所示。

(7)

(8)

式中：自變量x為溶脹時間t，因變量y為t/St。

均方根誤差RMSD分析回歸模型和實際值之間的偏差，如式(9)所示。

(9)

式中：ycalc為預測值，yi為實驗值，n為實驗數據點數量。均方誤差越小，預測值和實驗值差別越小，模型越準確。

2.2 二氧化碳擴散系數

通過可視窗可以觀察溶脹程度隨著時間的變化，在此基礎上計算二氧化碳在橡膠中的擴散系數。二氧化碳的擴散過程是氣體分子向高分子鏈段之間的自由空間遷移的過程。環境溫度在高分子材料的玻璃化轉變溫度以上時，溶劑分子向高分子體的擴散速率低于高分子鏈段運動的馳豫時間，溶脹過程由擴散步驟控制，二氧化碳的擴散對于橡膠的溶脹起決定作用，擴散過程遵循Fickian擴散機制。相反地，環境溫度在高分子材料的玻璃化溫度以下時，擴散速率比高分子鏈段運動的馳豫時間大，溶脹過程由網絡大分子鏈的松弛速率決定，擴散過程為non-Fickian擴散機制。根據Fick定律，二氧化碳向膠球樣品的遷移過程如式(10)所示。

(10)

式中：r為膠球中心到球體某一點的距離，C為樣品內溶劑的溶度，D為擴散系數。當樣品為球形，半徑為a時，Crank求得了該方程的解析解[13]52。

(11)

式中：Mt和M∞分別代表時間t和達到溶脹平衡時膠球內吸收二氧化碳的量。當t值較大，膠球接近溶脹平衡時，方程式(11)近似等于式(12)。

(12)

溶脹過程做如下假設：(1) 二氧化碳從膠球表面移動到中心的距離為半徑a，由下文研究可見，溶脹導致膠球的體積變化率并不大，因此這一假設不會導致顯著的誤差；(2) 二氧化碳被橡膠球吸收后立即導致其體積發生變化。基于以上假設，結合式(1)可得：

(13)

式中：St和Se分別為t時刻和溶脹平衡時的溶脹度，合并方程式(12)和式(13)得：

(14)

(15)

(16)

2.3 發泡橡膠回縮速率

ScCO2中充分溶脹的橡膠，一定速率泄壓會導致橡膠發泡，內部形成空隙，外部尺寸變大。恢復環境狀態后，由于硫化后的橡膠具有三維體型結構，發泡的橡膠會逐漸收縮，t時刻發泡橡膠膨脹度收縮到Sst。

(17)

收縮過程動力學表達式如式(18)所示。

(18)

積分上式得式(19)。

(19)

式中：Ss0和Sst是發泡后0時刻和t時刻膠球膨脹度；K3是收縮速率常數。

3 結果與討論

ScCO2中溶脹前后橡膠如圖2所示。由圖2可見，溶脹后橡膠尺寸變大，且整體形狀依然呈現球形，未出現流動和形狀變化異常等情況，因此可以通過觀察尺寸的變化分析溶脹過程。

(a) 溶脹前

(b)溶脹平衡溶脹條件：溫度為50 ℃，壓力為16 MPa圖2 通過可視窗觀察膠球的溶脹情況

3.1 膠球溶脹分析

不同溫度下膠球的溶脹規律如圖3所示。溶脹溫度分別為50 ℃和120 ℃，壓力為16 MPa。由圖3可見，溶脹溫度為50 ℃時，240 min達到溶脹平衡；而溫度為120 ℃時，120 min即達到溶脹平衡。根據分子熱運動理論，高溫導致二氧化碳分子的擴散性增強，高分子鏈段的移動性也會增強，因而溫度越高，膠球達到溶脹平衡的時間越短。溫度50 ℃達到溶脹平衡時，樣品B的溶脹度低于樣品A，樣品B的交聯密度為樣品A的2.4倍，更多的交聯位點使橡膠大分子鏈受到更多的束縛，從而溶脹度更小。然而，隨著溫度的升高，交聯密度更大的樣品B的平衡溶脹度增大，樣品A的平衡溶脹度變化不大。溫度為120 ℃時，樣品B的平衡溶脹度與樣品A相近，并且120 ℃時樣品的溶脹度要高于50 ℃時。根據Kojima的研究[15]175-181，二氧化碳密度和樣品溶脹度正相關，而隨著溫度的升高，相同壓力下二氧化碳的密度是降低的。顯然，溫度對于膠球的溶脹也有一定的影響。當溫度較高時，膠球受熱膨脹與溶脹作用共同使其體積增大。

t/min(a)

t/min(b)圖3 天然橡膠球在ScCO2中溶脹度隨時間的變化

3.2 溶脹動力學分析

根據溶脹動力學方程所得實驗結果如圖4所示。由式(3)和式(6)可知，如果溶脹過程符合動力學方程，實驗值擬合后是一條直線。然而，當溶脹時間低于60 min時，一階和二階方程計算實驗數據的線性度均較差，并且由圖4(b)可見，0～60 min時二階方程完全不呈線性趨勢。產生這一現象，是由于0～60 min屬于程序升溫階段，該階段的溶脹屬于升溫溶脹，而不是等溫溶脹，因此動力學擬合結果較差。溶脹溫度為50 ℃時，由于目標溫度較低，而反應釜功率是一定的，當溫度接近50 ℃時，溫升較慢，所以溫升階段接近100 min。

等溫階段的反應動力學分析如圖5所示，由式(3)和式(6)線性擬合等溫溶脹階段實驗數據，擬合度R2如表2所示。由表2可見，一階和二階動力學方程均能較好地預測溶脹過程。溫度為50 ℃時，溶脹過程符合二階動力學過程，而當溶脹溫度升高到120 ℃時，溶脹過程更符合一階動力學過程。

t/min(b)圖5 天然橡膠球在ScCO2中一階(a)和二階(b)溶脹動力學擬合曲線

表2 溶脹動力學方程擬合度R2

反應動力學常數K如表3所示，K1和K2分別代表一階和二階動力學方程。隨著溫度的升高，K1和K2均顯著增大，表明溶脹速率加快。這一結果與圖3一致，圖3中隨著溶脹溫度的升高，膠球更快達到溶脹平衡。

表3 溶脹動力學常數K

由式(9)計算動力學擬合方程的RMSD，結果如表4所示，均方根誤差和響應值相比差距均較小，表明模型的預測值ycalc和實際實驗yi值吻合度高。

表4 式(6)回歸方程系數和RMSD

3.3 二氧化碳在膠球中的等溫擴散系數

t/sa

t/sb圖6 不同溫度溶脹時間t隨ln(1-St/Se)的變化

表5 二氧化碳在天然橡膠球中的等溫擴散系數

3.4 發泡膠球收縮動力學分析

天然橡膠球在ScCO2中達到溶脹平衡后，以一定的速率泄壓，本研究的泄壓速率為0.5 MPa/min，由于橡膠所處環境壓力降低，橡膠內吸收的的氣體由于內外壓差快速膨脹，導致橡膠發泡。樣品A發泡前后尺寸對照如圖7所示，原膠球直徑為14 mm，發泡膠球直徑為31 mm。

溶脹條件：溫度為50 ℃，壓力為16 MPa，時間為6 h圖7 溶脹前后天然橡膠球尺寸

發泡后的橡膠從反應釜取出置于環境狀態下，如圖8所示，膨脹度隨時間的增加線性減小。根據式(19)，ln(Ss0/Sst)隨時間的變化如圖9所示，直線斜率即為收縮速率常數K3，樣品A和B的收縮速率常數分別為5.14×10-6min-1和7.11×10-6min-1。樣品B的交聯密度是樣品A的2.4倍，而ScCO2中平衡溶脹度相近，但發泡后的膨脹度分別為9.7和6.3，且樣品B的收縮速率比樣品A高38%。

t/min圖8 不同交聯密度橡膠膨脹度隨時間t的變化

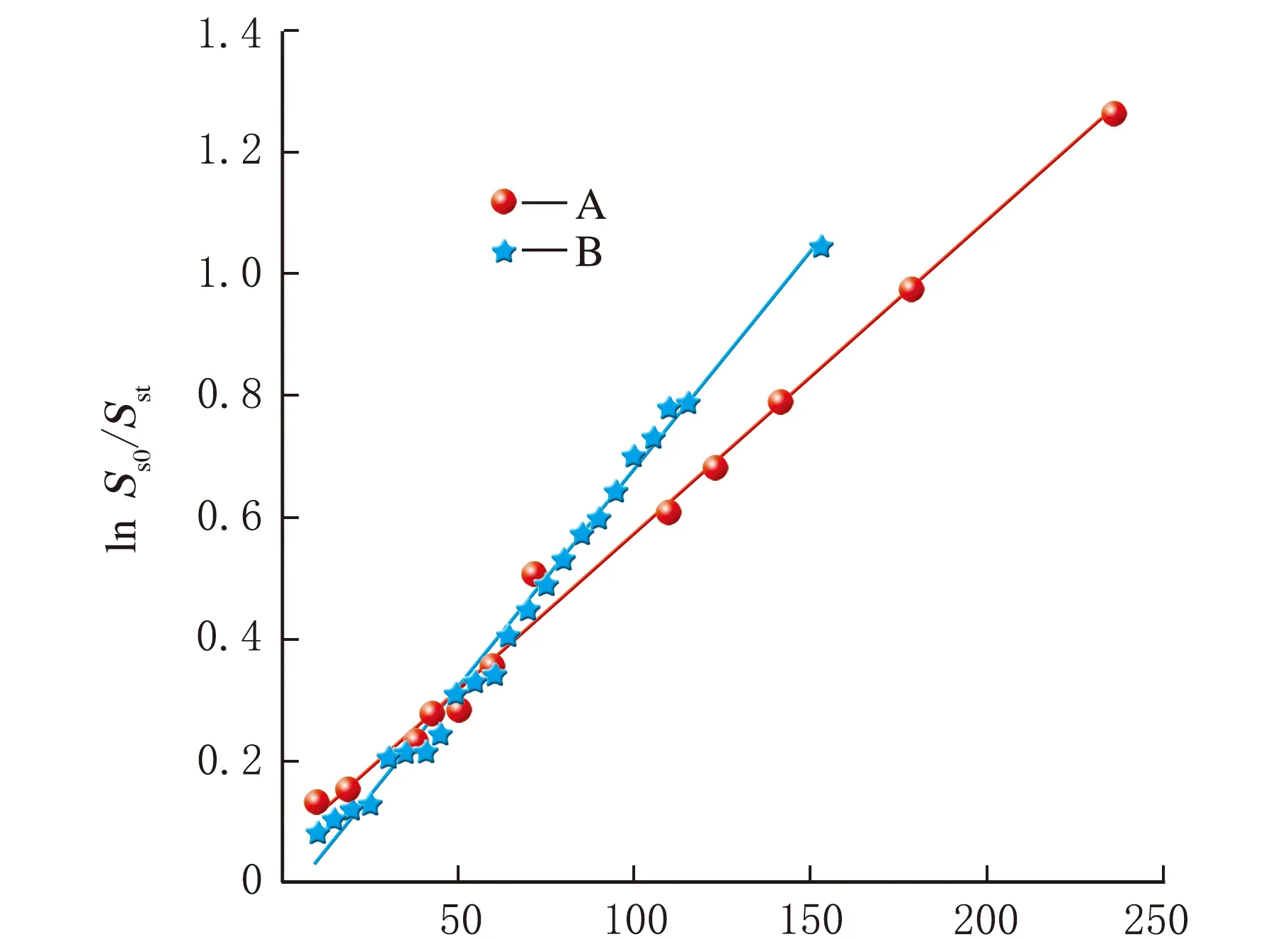
t/min圖9 ln(Ss0/Sst)隨時間t的變化

可見，交聯密度對于橡膠在ScCO2中的溶脹過程并無顯著影響，但是對于發泡后橡膠的膨脹率以及收縮速率有顯著影響。Nikitin報道[12]939，交聯密度增大到一定程度，吸收二氧化碳的量并無太大差別，因而溶脹度差別不大。但膨脹后橡膠的交聯網絡伸展，分子排列趨于有序，根據熵增原理，高分子鏈有收縮、卷曲、無序化的趨勢，因此交聯密度大的橡膠，由于大分子鏈段受到更多的束縛，膨脹率更小，收縮速率更快。

4 結 論

(1)溶脹溫度的升高對不同交聯密度橡膠的影響不同。溫度從50 ℃升高到120 ℃，交聯密度為0.78×10-4mol/cm3樣品A的溶脹度變化不大，而交聯密度為1.9×10-4mol/cm3樣品B的溶脹度逐漸增大。

(2)一階和二階動力學方程均能較好地預測溶脹過程。溫度為50 ℃時，溶脹過程符合二階動力學方程，而溫度為120 ℃時，溶脹過程更符合一階動力學方程。溫度為120 ℃時溶脹速率更快，相應的動力學常數顯著增大。

(3)溫度為120 ℃時，二氧化碳在天然橡膠球中的擴散系數約為50 ℃時的2倍，而交聯密度對于擴散系數并無顯著影響。

(4)交聯密度對于發泡后橡膠的膨脹率以及收縮速率影響顯著。本研究中樣品B的交聯密度是樣品A的2.4倍，ScCO2中平衡溶脹度相近，發泡后的膨脹度分別為9.7和6.3，樣品B的收縮速率比樣品A高38%。