改進直覺模糊熵和證據推理的多屬性群決策方法
2021-08-02 10:31:58高一凌龔本剛張孝琪
安徽工程大學學報 2021年3期
高一凌,龔本剛,張孝琪
(安徽工程大學 經濟與管理學院，安徽 蕪湖 241000)
由于決策問題的復雜性和決策環境的不確定性等原因，決策者在實際決策過程中往往難以獲取精確的評估參數。為了更好地刻畫決策信息的模糊性，Zadeh于1965年提出模糊集理論，之后Atanassov引入非隸屬度將其進一步完善，建立了直覺模糊集(Intuitionistic Fuzzy Sets)。直覺模糊集拓展了模糊集中“非此非彼”的思想，為決策者提供了更豐富的手段來描述不確定性評價信息。因而，自提出以來在管理決策領域得到快速發展和應用，相關研究集中在集結算子、得分函數、不確定性測度、相似度度量和直覺模糊熵等方面。
直覺模糊集理論通過隸屬度和非隸屬度以及猶豫度來靈活地刻畫評估信息。然而，在實際決策過程中，該理論在引入新參數的同時，也給決策矩陣和數據收集增加了不確定性。在模糊集中，熵可以作為不確定性的一種度量方式。由此，直覺模糊集的熵引起了相關學者的關注，在Burillo提出最初的直覺模糊熵和Szmidt給出其公理化定義后，直覺模糊熵及其公理化定義不斷地得到拓展。如Verma在Atanassov直覺模糊集理論基礎上提出了一種指數直覺模糊熵測度；趙飛認為直覺模糊集的不確定性由未知信息的直覺不確定性和已知信息的模糊不確定性共同構成，并且直覺模糊熵應是唯一的，由此提出一種直覺模糊熵的公理化定義并構造了新的度量方法；高明美從直覺模糊集的隸屬度與非隸屬度之間的距離以及猶豫度對直覺模糊熵的貢獻角度出發，改進公理化定義并構造新的直覺模糊熵的計算公式。
在考慮直覺模糊多屬性決策的情形下，Yuan給出一類新直覺模糊熵并將其與幾種傳統直覺模糊熵定義的權重結果進行了仿真分析，結果表明權重不僅依賴于熵的定義，而且依賴于備選方案和屬性的個數；陳業華提出一類改進的直覺模糊熵并將其應用于應急決策中;王堅強將直覺模糊熵運用到直覺語言集中去，構建最優權重模型，并通過直覺語言加權算術平均算子實現對評價信息的集結;江文奇針對準則值為區間直覺模糊數且準則權重為區間數的多準則決策問題，提出基于二元聯系數的區間直覺模糊型多準則決策方法。
證據推理方法是對D-S(Dempster-Shafer)證據理論的發展，它在處理不確定性、模糊性的多屬性決策問題中具有明顯優勢，并得到廣泛應用。該方法通過正交和運算將多源評價信息進行集結得到結果。代文鋒將Burillo提出的直覺模糊熵和證據推理方法相結合，提出多屬性群決策方法;Bao考慮決策者對猶豫不決度的偏好，定義了直覺模糊集的熵和交叉熵測度,提出了一種基于前景理論和證據推理方法的直覺模糊決策方法。因此，采用證據推理方法對含有較強猶豫性、模糊性和不確定性的決策信息進行集結，能較好地保證決策信息的完整性。
綜上所述，上述學者分別從不同角度提出了直覺模糊熵的公理化定義，有利于實現直覺模糊多屬性決策。然而現有的公理化定義描述部分直覺模糊集的不確定性特征并不準確或者不全面，例如不能區分(0.5,0.5)、(0.4,0.4)這類隸屬度與非隸屬度相等直覺模糊集的模糊性，導致部分文獻定義的直覺模糊熵公式在某些情形下不能精確度量熵值，進而影響多屬性決策結果。于是，研究首先分析了現有直覺模糊熵公式與不確定性的匹配度，在完善直覺模糊集不確定性度量問題的基礎上，改進了直覺模糊熵公理化定義，進而構造一類改進的直覺模糊熵公式，提出一種基于改進直覺模糊熵和證據推理的多屬性群決策方法，最后利用算例分析闡明方法的有效性。
1 直覺模糊熵的改進
1.1 直覺模糊熵的概念與分析
定義
1 若E
滿足如下準則，稱實值函數E
:IFS
(X
)→[0,1]為直覺模糊熵。條件1：E
(A
)=0當且僅當A
是經典集；條件2：E
(A
)=1當且僅當?x
∈X
，有μ
(x
)=υ
(x
)；條件3：E
(A
)=E
(A
)；條件4：當μ
(x
)≤υ
(x
)時，有μ
(x
)≤μ
(x
),υ
(x
)≥υ
(x
)；或當μ
(x
)≥υ
(x
)時，有μ
(x
)≥μ
(x
),υ
(x
)≤υ
(x
)，則都有E
(A
)≤E
(B
)成立。基于以上常用的直覺模糊熵的定義，Szmidt，Verma，Yuan，陳業華和王堅強等給出了不同的直覺模糊熵公式，分別記為E
(A
)-E
(A
)，具體公式如下：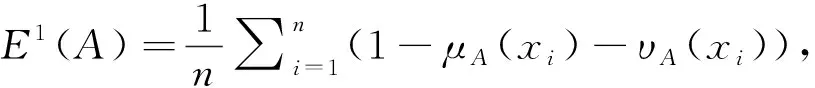
(1)
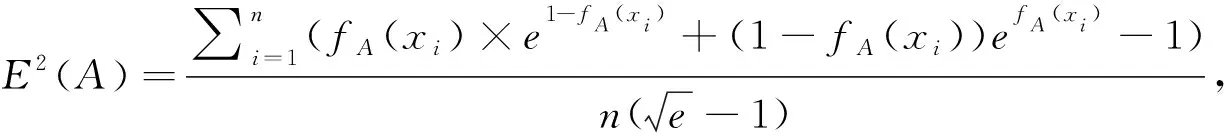
(2)
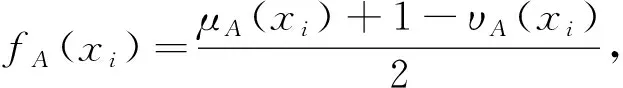
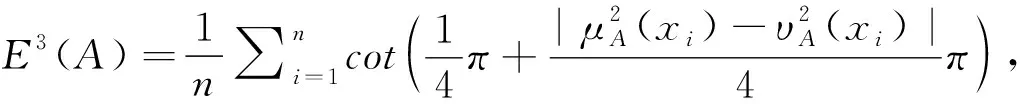
(3)
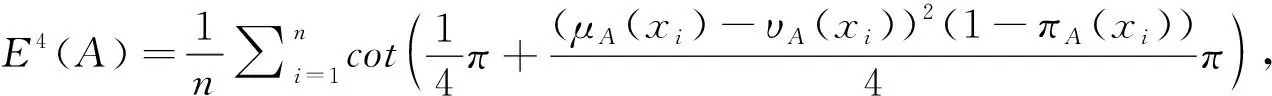
(4)
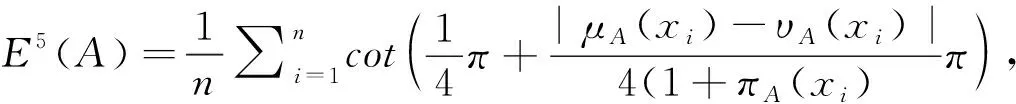
(5)
E
(A
)-E
(A
)均根據上述公理化定義構造，部分學者對約束條件做出了改進，如趙飛、高明美將改進的直覺模糊熵記為E
(A
)和E
(A
)，如式(6)、式(7)所示。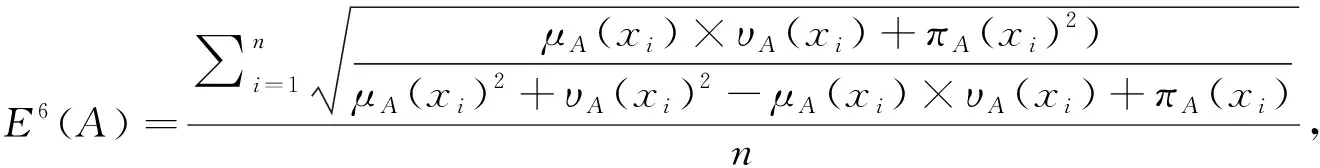
(6)
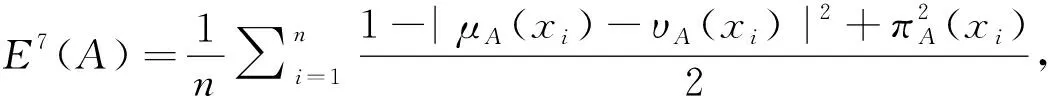
(7)
上述的E
(A
)-E
(A
)在一定范圍內具有適用性，但還存在部分缺陷，具體分為兩個方面。(1)最大直覺模糊熵的取值問題。根據定義1中條件2，直覺模糊集中的隸屬度等于非隸屬度時不確定度最高，直覺模糊熵達到最大值。忽略了實際決策時支持與反對信息雖然相同，但依舊包含著部分有效信息的情況。因此將定義1中條件2修改為，當隸屬度與非隸屬度相等且為0時，直覺模糊熵達到最大值更為合理。
(2)忽略猶豫度的影響。猶豫度相等時，直覺模糊熵與隸屬度和非隸屬度的差值負相關，即差值越小表示不確定程度越高，熵值越大；隸屬度與非隸屬相等且不為0時，猶豫度越大代表不確定性越大，熵值也越大。另外，直覺模糊集的不確定性除了來自未知信息，即猶豫度的影響，還包括直覺模糊集中已知信息的模糊度。因此直覺模糊集的不確定性必定不會小于猶豫度。可將定義1的條件擴展以便更好地描述直覺模糊熵。
1.2 改進直覺模糊熵的提出
綜上分析，對已有的直覺模糊熵公理化定義做出以下改進與拓展。
定義
2 若E
滿足如下準則，稱實值函數E
:IFS
(X
)→[0,1]為直覺模糊熵。條件1：E
(A
)=0，當且僅當A
是一個分明集；條件2：E
(A
)=1，對?A
∈IFS
(X
),當μ
(x
)=υ
(x
)=0時成立；條件3：當π
(x
)=π
(x
)時，若|μ
(x
)-υ
(x
)|≤|μ
(x
)-υ
(x
)|，則E
(A
)≥E
(B
)；或當|μ
(x
)-υ
(x
)|=|μ
(x
)-υ
(x
)|時，若π
(x
)≥π
(x
)，則E
(A
)≥E
(B
)；條件4：當μ
(x
)≤υ
(x
)時，有μ
(x
)≤μ
(x
),υ
(x
)≥υ
(x
)；或當μ
(x
)≥υ
(x
)時，有μ
(x
)≥μ
(x
),υ
(x
)≤υ
(x
)，則E
(A
)≤E
(B
)；
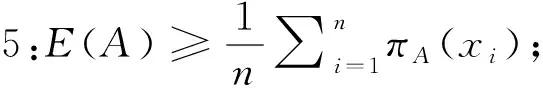
E
(A
)=E
(A
)。由此基于定義2，研究構造一類改進直覺模糊熵公式，以便較好區分直覺模糊集的模糊性。對于任意的直覺模糊集{[x
,μ
(x
),υ
(x
)]|x
∈X
,i
=1,2,…,n
}，π
(x
)=1-μ
(x
)-υ
(x
)代表猶豫度。定義直覺模糊熵：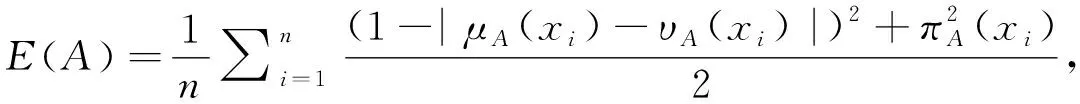
(8)
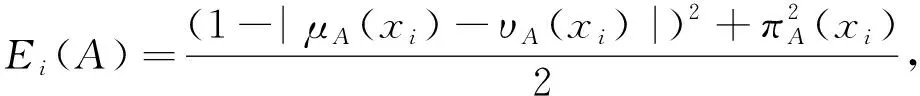
(9)
下面證明研究提出的熵符合定義2中的6個約束條件：
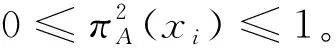
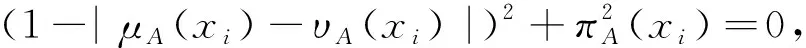
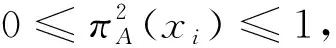
μ
(x
)=υ
(x
)=0，則可得E
(A
)=1，因此E
(A
)=1。
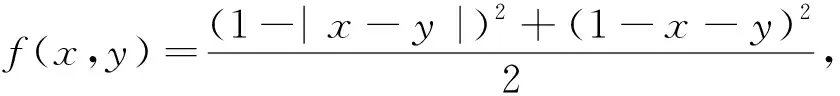
μ
(x
)≤υ
(x
)時，有μ
(x
)≤μ
(x
),υ
(x
)≥υ
(x
)，f
(μ
(x
),υ
(x
))≤f
(μ
(x
),υ
(x
))；同理，當μ
(x
)≥υ
(x
)時，有μ
(x
)≥μ
(x
)，υ
(x
)≤υ
(x
)，f
(μ
(x
),υ
(x
))≤f
(μ
(x
),υ
(x
))。因此，當A
≤B
時，則有E
(A
)≤E
(B
)，故E
(A
)≤E
(B
)成立。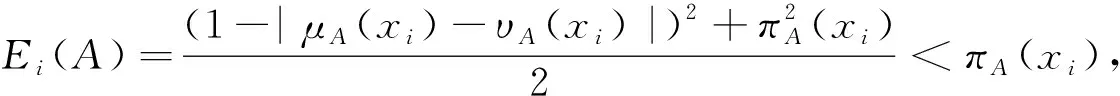
A
={[x
,υ
(x
),μ
(x
)]|x
∈X
,i
=1,2,…,n
}，故E
(A
)=E
(A
)。1.3 改進直覺模糊熵的優勢說明
綜上分析，改進直覺模糊熵公式符合拓展及修改后的直覺模糊熵公理化定義。從算例和圖像兩個方面來說明改進的直覺模糊熵的有效性，進而指出其他公式可能存在的缺陷。
(1)從算例來看，分別用E
(A
)～E
(A
)與研究提出的E
(A
)計算以下直覺模糊集(A
～A
)，結果如表1所示。從表1可以看出：①E
(A
)和E
(A
)沒有將猶豫度考慮進去，用E
(A
)計算猶豫度相等的直覺模糊集(如A
、A
與A
)，結果均相等；用E
(A
)計算隸屬度與非隸屬度差值相等的直覺模糊集(如A
和A
)，結果相等。根據定義2中條件3可知，E
(A
)>E
(A
)>E
(A
)，E
(A
)>E
(A
)結果合理。②用E
(A
)～E
(A
)計算隸屬度與非隸屬相等且不為0的直覺模糊集(如A
、A
與A
)，計算結果均為最大值。根據定義2中條件2和條件3可知，E
(A
)<E
(A
)<E
(A
)，結果合理。③E
(A
)和E
(A
)存在對部分直覺模糊集無法區分的缺陷，如E
(A
)對A
和A
、E
(A
)對A
和A
在區分不確定度時失效。但E
(A
)可清晰區分。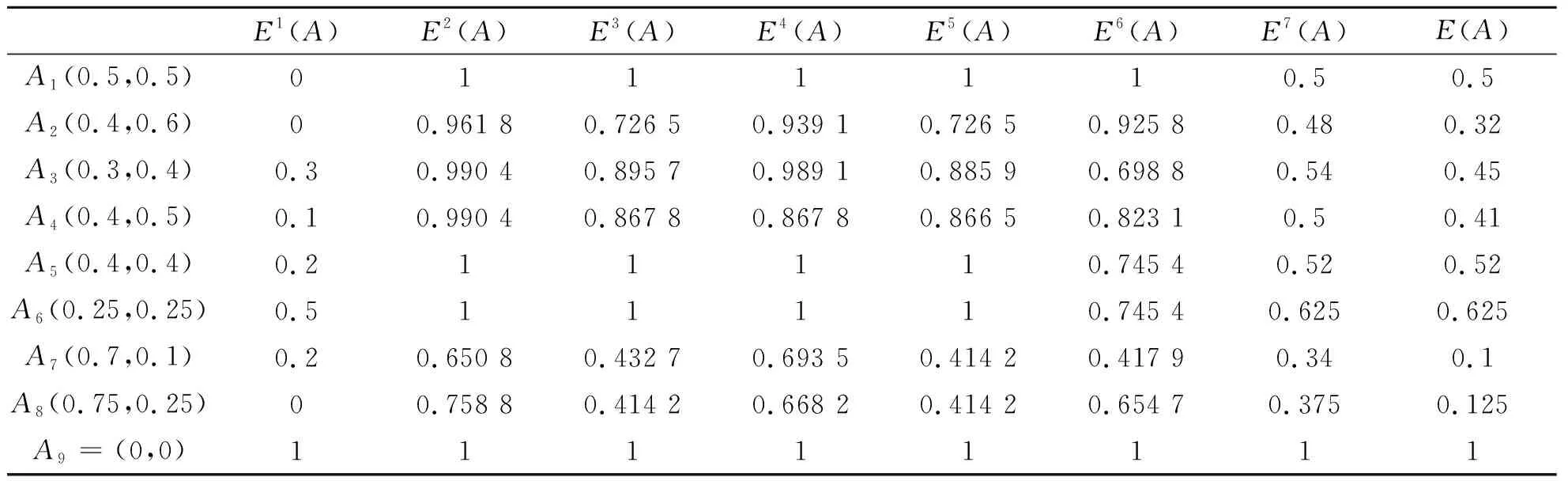
表1 不同直覺模糊熵值的比較
(2)從圖像來看，E
(A
)～E
(A
)與研究提出的E
(A
)的三維圖像如圖1～圖8所示。由圖1～圖8可以看出：①當μ
(x
)=υ
(x
)=0時，E
(A
)～E
(A
)及E
(A
)都取得最大值1，并且E
(A
)～E
(A
)及E
(A
)的圖像都具有對稱性。②從圖1～圖6可以看出，它們都有兩個及兩個以上的點對應著最大值1或最小值0，因此可能存在對不同的直覺模糊集的不確定性度量不精準的問題。而圖7、圖8較為類似，但E
(A
)在區分隸屬度或非隸屬度為0.5的直覺模糊集時失效，而由圖8可以看出不同的直覺模糊集所對應的E
(A
)均不同，表明E
(A
)具有較好的區分性，不會出現熵值相同情況。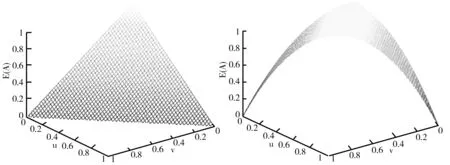
圖1 E1(A)三維函數圖 圖2 E2(A)三維函數圖
綜上所述，根據修改后的直覺模糊熵公理化定義構建的E
(A
)可較好彌補上述公式的不足，區分直覺模糊集的模糊性時具有合理性和有效性。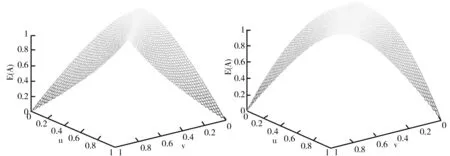
圖3 E3(A)三維函數圖 圖4 E4(A)三維函數圖
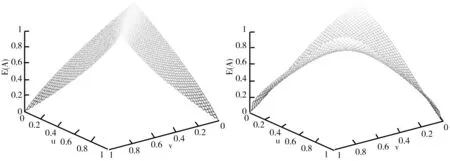
圖5 E5(A)三維函數圖 圖6 E6(A)三維函數圖
圖7 E7(A)三維函數圖 圖8 E8(A)三維函數圖
2 直覺模糊多屬性群決策方法
針對決策信息為直覺模糊數，且屬性權重與專家權重完全未知或屬性權重與專家權重部分已知的多屬性決策問題,首先，依據改進的直覺模糊熵對決策矩陣中屬性的不確定性進行度量，求出屬性權重和專家權重，利用證據推理方法進行信息的融合，并根據與理想解的Hamming距離進行排序。具體決策過程如下：
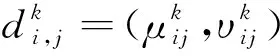
Step 1 屬性權重的求解。
越小的直覺模糊熵值意味著更小的不確定程度和更多的確定性信息，屬性的權重應使得所有屬性的總熵值最小，H
表示屬性權重已知的約束條件集合，由此建立權重優化模型如下: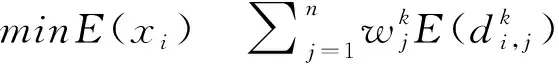
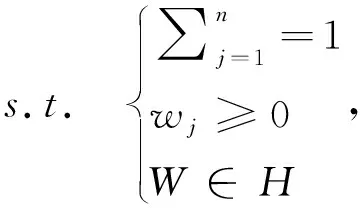
(10)
在屬性權重完全未知的情況下，得到屬性權重為：
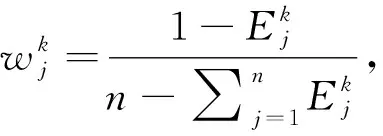
(11)
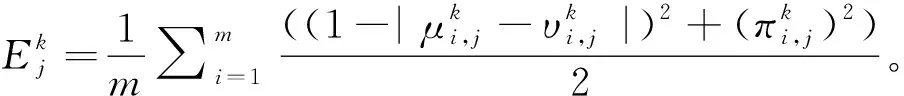
(12)
Step 2 基于證據推理的綜合直覺模糊集的形成。
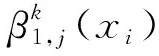
(13)
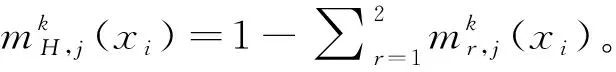
(14)
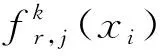
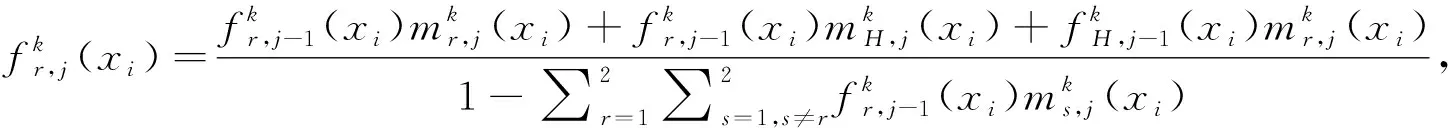
(15)
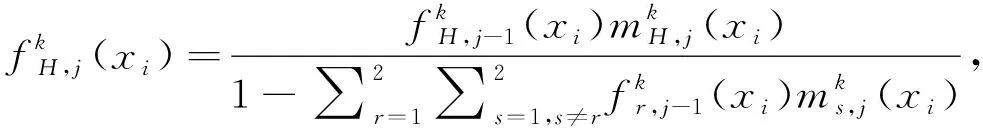
(16)
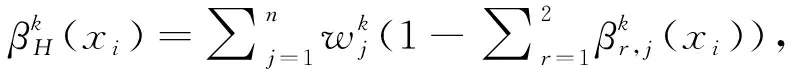
(17)
(18)
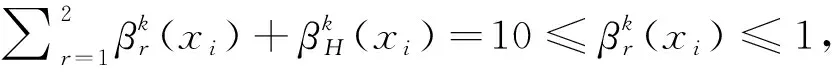
(19)
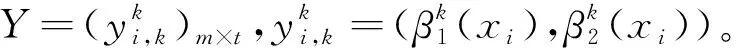
Step 3 基于綜合直覺模糊熵值的專家權重求解。
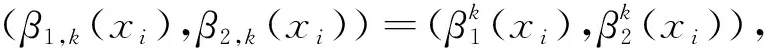
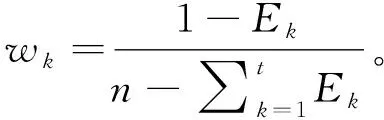
(20)
Step 4 最終直覺模糊集形成。
依據Step 2求得方案x
的支持度β
(x
)及未分配等級的β
(x
)，可得最終決策矩陣Q
=(q
)×1，q
=(β
(x
),β
(x
))。具體公式如下：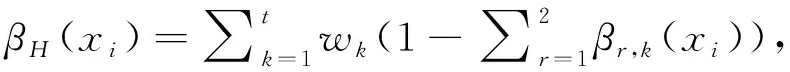
(21)
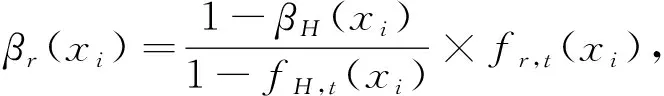
(22)
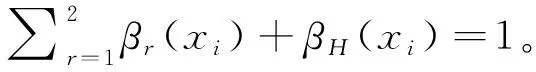
(23)
Step 5 計算各方案與理想解的相對貼近度，最后選擇最佳方案。
正理想點記為X
=(1,0)，負理想點記為X
=(0,1)。方案x
的最終直覺模糊值與正、負理想方案之間的Hamming距離為：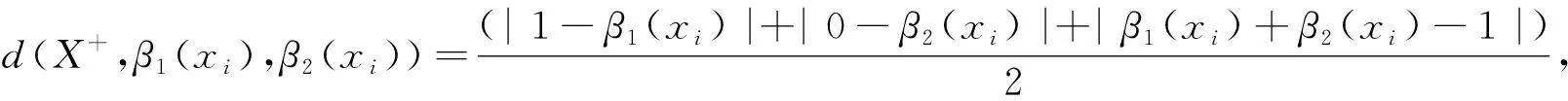
(24)
(25)
式中，d
(X
,β
(x
),β
(x
))∈[0,1]，0≤β
(x
)+β
(x
)≤1，0≤β
(x
)≤1，0≤β
(x
)≤1，1≤i
≤m
。各方案與理想解的相對貼近度S
如式(26)所示。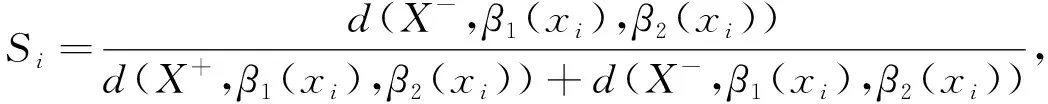
(26)
按照相對貼近值從大到小對方案進行排序，相對貼近度越大的方案越好。
3 算例分析
采用文獻[16]的案例數據來驗證研究方法的合理性，3個專家(P
～P
)對4個候選人(x
～x
)，從工作態度、學術能力、教學經驗和品德4個方面(C
～C
)進行打分，最終挑選出最優者。運用式(10)～式(12)計算不同專家的屬性權重，結果如表2所示。
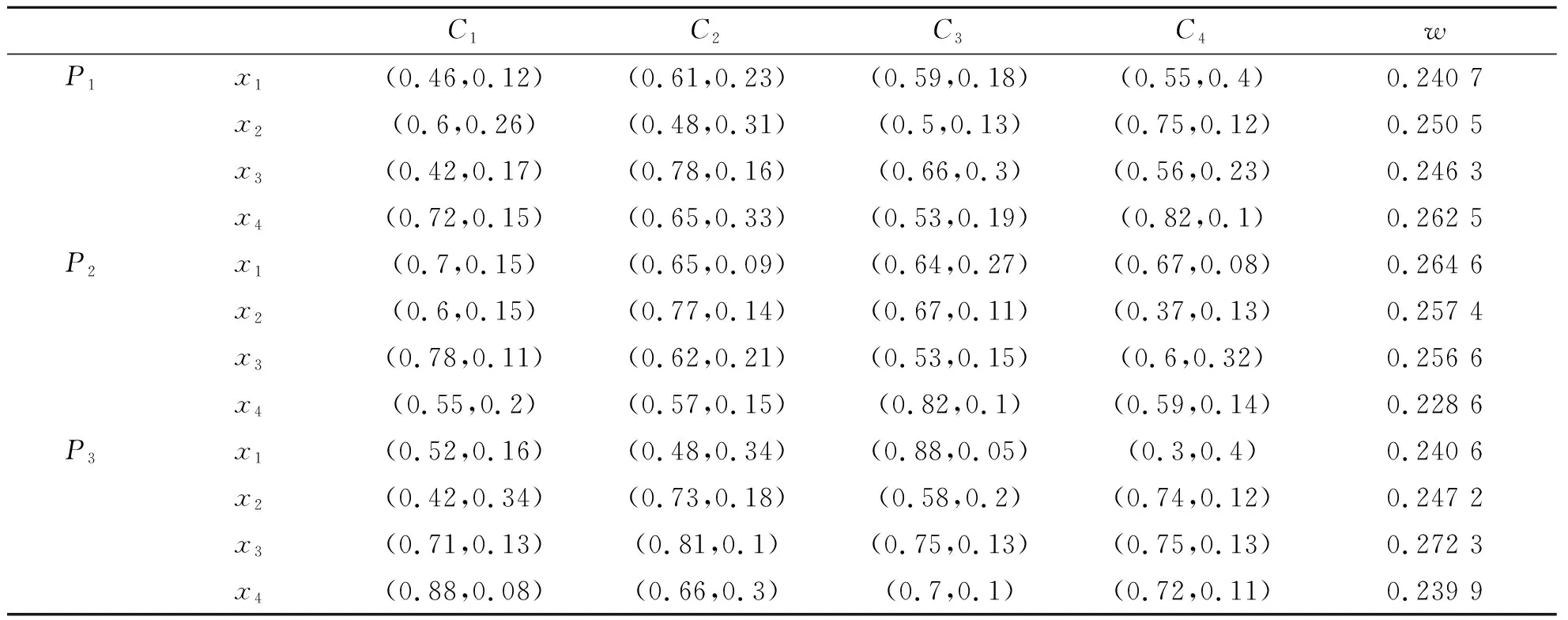
表2 各專家決策信息及屬性權重
根據表3，運用式(13)～式(25)求得最終決策結果與排序，并與文獻[16]方法做比較，結果如表3所示。由表3可以看出：①研究方法求得最佳的候選人是x
，其次是x
，與文獻[16]相比兩種方法求得的最優候選人結果是一致的，說明研究方法的可行性。②研究方法與文獻[16]比較而言，x
和x
評價結果有所差別，差異的原因是兩種方法采用的直覺模糊熵不同，導致求得屬性和專家權重不同從而影響排序結果。文獻[16]方法中采用了1.1中所提到的E
(A
)，但由1.3中表1與三維函數圖像分析表明，E
(A
)在區別隸屬度與非隸屬相等且不為0的直覺模糊集(如A
(0.5,0.5)、A
(0.4,0.4)和A
(0.25,0.25))時失靈，研究方法采用的E
(A
)在特定情形下對直覺模糊集不確定程度的度量要優于E
(A
)，因此,研究方法在解決直覺模糊多屬性決策問題時比文獻[16]方法更為合適。
表3 研究方法與文獻[16]決策結果的比較
為了進一步驗證方法的科學性和合理性，將研究方法與文獻[6]中算例進行對比。通過3個專家依據5個評價指標對4家供應商進行選擇，兩種方法進行求解的計算結果如表4所示。通過決策結果可以看出，研究方法與文獻[6]方法挑選的最優供應商都是x
。文獻[6]方法是利用算子解決直覺模糊多屬性決策問題，研究方法是從直覺模糊熵來刻畫不確定性，再利用證據理論對不確定信息融合的方法解決直覺模糊多屬性決策問題。雖然兩者方法不同，但是最優結果相同，從一定程度上說明了研究方法的可行性和合理性。
表4 研究方法與文獻[6]決策結果的比較
4 結論
為解決決策信息為直覺模糊數且屬性權重或專家權重完全未知與部分已知的多屬性決策問題，提出一種基于改進的直覺模糊熵和證據推理的決策方法。研究在進一步完善了直覺模糊熵公理化定義的基礎上，設計了一類改進的直覺模糊熵公式，克服了在某些情形下不能區分和度量直覺模糊集的不確定性問題，為解決直覺模糊多屬性問題提供思路，最后通過與文獻[16]的比較說明了研究方法的可行性。研究模型沒考慮區間型和梯形的直覺模糊數，針對這兩種直覺模糊熵的度量也是未來進一步研究的方向。
猜你喜歡
中華手工(2017年2期)2017-06-06 23:00:31
Coco薇(2016年2期)2016-03-22 02:42:52
山東青年(2016年1期)2016-02-28 14:25:25
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年4期)2015-05-19 14:47:56
中外會展(2014年4期)2014-11-27 07:46:46
當代修辭學(2014年3期)2014-01-21 02:30:44
公務員文萃(2013年5期)2013-03-11 16:08:37
海外英語(2006年11期)2006-11-30 05:16:56
祝您健康(1987年3期)1987-12-30 09:52:32
