利用面片法向量保留模型特征的3D打印自適應(yīng)分層算法

朱敏,黨元清,高思煜,高強

(1.哈爾濱工業(yè)大學(xué)電氣工程及自動化學(xué)院,150001,哈爾濱; 2.哈爾濱工業(yè)大學(xué)機電工程學(xué)院,150001,哈爾濱)

3D打印技術(shù)是利用計算機技術(shù)逐層堆積打印出立體模型的方法。隨著3D打印技術(shù)的不斷普及和應(yīng)用,打印精度和打印效率越來越受到重視。分層處理是3D打印中的重要一環(huán)。研究表明,三維打印精度和打印效率都與分層厚度有著緊密聯(lián)系[1]:分層厚度越小,打印精度越高,但打印效率較低;增大層厚雖然可以提高打印效率,但會產(chǎn)生較大的臺階誤差,而且容易導(dǎo)致模型特征的缺失,使打印精度大大降低,因此如何優(yōu)化分層厚度至關(guān)重要。

現(xiàn)有的分層算法根據(jù)分層厚度是否可變主要分為等層厚分層算法和自適應(yīng)分層算法。等層厚分層算法過程簡單,易于實現(xiàn),但是由于層厚固定,打印效率和打印精度不可兼得;自適應(yīng)分層算法根據(jù)模型表面特征等要求自動調(diào)節(jié)分層厚度,協(xié)調(diào)了打印精度與打印效率之間的關(guān)系[2],具有明顯優(yōu)勢。目前自適應(yīng)分層算法處理的模型數(shù)據(jù)類型主要有STL模型、精確CAD模型和點云數(shù)據(jù)[3]。由于CAD模型常存在系統(tǒng)兼容性差和編輯環(huán)境復(fù)雜等問題,點云模型存在模型雜亂不規(guī)則、數(shù)據(jù)量龐大等問題[4-5],因而在分層切片算法中應(yīng)用較少。STL模型的三角面片與分層平面的相交求解算法計算簡單,同時它也是目前大部分3D打印設(shè)備系統(tǒng)支持的標準輸入文件格式,因此本文選用STL模型研究自適應(yīng)分層算法。

目前自適應(yīng)分層算法確定層厚的依據(jù)主要有垂直分層輪廓曲線上點的切線角、模型表面曲率、面積變化率、三角面片法向量等。文獻[6-7]利用垂直切片輪廓線上點的切線角確定分層切片的厚度,但該算法需要采樣提取模型的垂直輪廓線,未提取輪廓線的部分易遺漏模型特征。文獻[8-10]利用曲面在分層方向上的法曲率確定分層厚度,但是計算曲面上任意給定點的曲率比較復(fù)雜,而且在每次分層中需求出大量點的曲率,增加了算法的難度和復(fù)雜度。文獻[11-14]通過比較相鄰兩層切片的面積來推測模型表面的幾何特征,但是由于基準面積會發(fā)生變化,因此精度難以控制,而且如果相鄰兩層面積相同則該算法不再適用。文獻[15-17]利用三角面片的法向量實現(xiàn)切片算法,計算過程簡單但是僅考慮了臺階效應(yīng)的影響。國內(nèi)外學(xué)者還提出一些其他算法,文獻[18]通過計算尖端高度對相鄰層進行合并;文獻[19]通過確定最優(yōu)分層方向減小臺階誤差;文獻[20]將STL模型轉(zhuǎn)換為改進邊界八叉樹數(shù)據(jù)結(jié)構(gòu)后再計算分層厚度;文獻[21-22]在具有曲面形狀的特征部位采用曲面分層,普通部位則采用平面分層。通過文獻調(diào)研發(fā)現(xiàn),目前自適應(yīng)分層算法的研究主要集中于如何在盡可能減少分層層數(shù)的情況下減小模型的臺階誤差等問題,對于影響打印精度的模型特征丟失現(xiàn)象研究較少。文獻[23-24]雖指出了模型特征的相關(guān)概念,但將特征點定義為局部最高或最低點具有一定的局限性,例如對于類似于馬鞍面鞍點的復(fù)雜點無法識別。文獻[25-26]通過建立體積誤差模型實現(xiàn)自適應(yīng)分層,但當存在未被切割的三角面片時,可能難以得到準確的分層厚度或者會導(dǎo)致特征遺失、體積偏差大等問題。

針對目前自適應(yīng)分層算法計算復(fù)雜、不能有效反映模型特征的問題,本文提出一種基于STL模型中三角面片法向量的改進自適應(yīng)分層算法。一方面,利用STL模型中的三角面片法向量信息進行分層,提取方便且計算簡單;另一方面,該算法不僅考慮削弱臺階效應(yīng),還對模型特征進行識別和保留,有利于提高打印精度。

1 STL模型信息讀取與存儲

STL文件有ASCII和二進制兩種形式,二者均包含模型中所有三角面片的頂點坐標及法向量信息,如圖1所示。

(a)ASCII

(b)二進制

實現(xiàn)自適應(yīng)分層前需要對STL文件中包括法向量在內(nèi)的模型信息進行提取并作為后續(xù)計算的基礎(chǔ)。本算法遍歷STL文件中的每一個三角面片,利用哈希表濾去冗余數(shù)據(jù),分別建立點表、面表存儲信息。其中點表中的每個點都分配有點索引值,包含點的三維坐標、點所在面的索引值信息;面表中的每個面都分配有面索引值,包含面的三個頂點索引值、面的法向量、三個鄰面索引值信息,存儲結(jié)構(gòu)如圖2所示。該模型的讀取與存儲形式不僅方便點、面之間拓撲關(guān)系的重建,還可以減小數(shù)據(jù)的冗余度,節(jié)省內(nèi)存[27]。

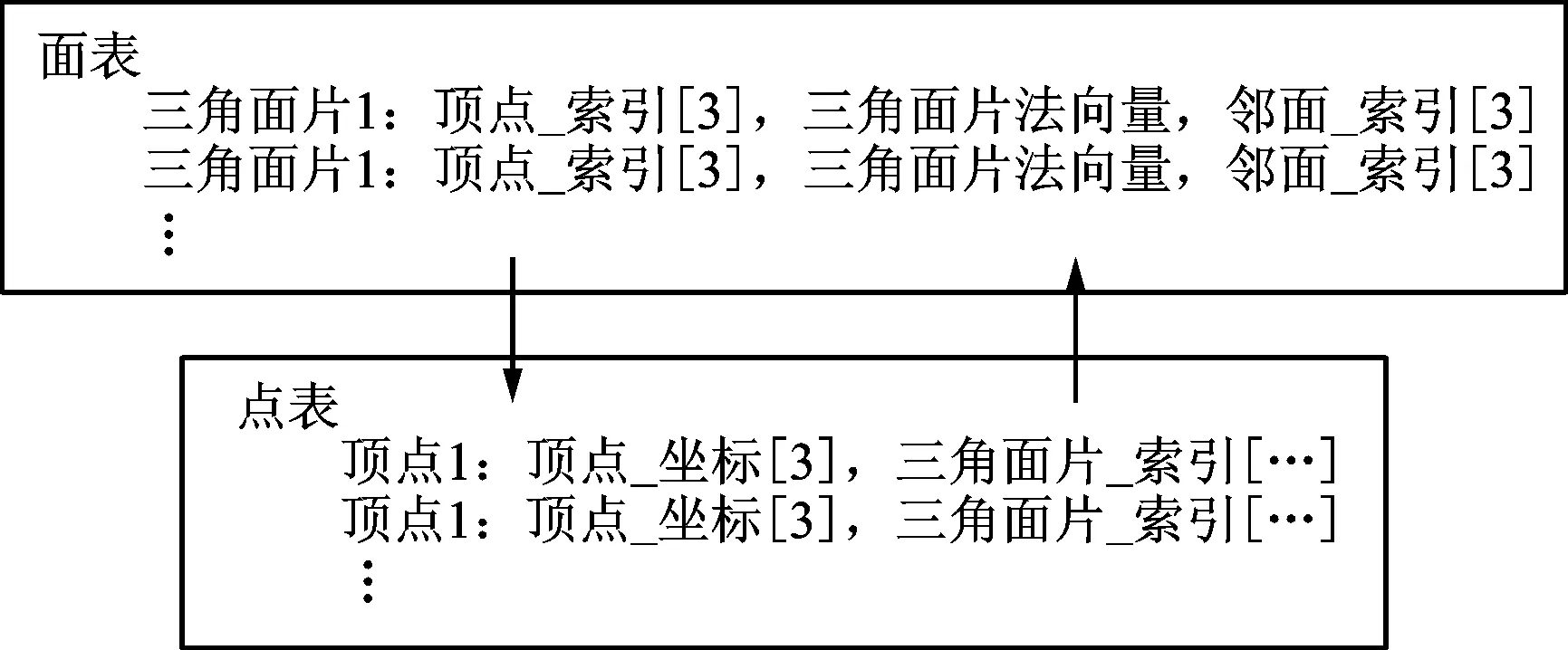
圖2 點表與面表結(jié)構(gòu)圖Fig.2 Structure diagram of point table and surface table

2 自適應(yīng)分層算法分析

2.1 減小臺階效應(yīng)的分層算法

臺階效應(yīng)是產(chǎn)生模型誤差的一個主要因素,是由增材制造的原理造成的。增材制造實質(zhì)為先分層后堆積。分層是利用垂直于分層方向的平行平面去截三維模型從而獲得截面層片的過程。當層片厚度趨于無窮小時,打印實體與三維模型相同。但是受實際制造工藝等因素的制約,層片厚度的取值介于打印設(shè)備和工藝所允許的最大值與最小值之間。因此打印實體和輸入的三維模型就有所偏差,即臺階效應(yīng)。特別是當分層方向偏離模型表面一定角度時,3D打印會產(chǎn)生明顯的臺階效應(yīng)。如圖3所示,STL模型中三角面片的臺階誤差(陰影部分)與分層厚度d、該面片的傾斜角度α有關(guān)。在面片傾斜程度一定的情況下,分層厚度越小,臺階效應(yīng)越小;當分層厚度不變時,模型表面在分層處傾斜角度越大,臺階效應(yīng)越小。因此在三角面片傾斜角度小的地方采用較小層厚,可削弱臺階效應(yīng)。

圖3 臺階效應(yīng)示意圖Fig.3 Schematic diagram of step effect

設(shè)定Z軸正方向為打印方向,則三角面片與分層平面之間的夾角α∈[0°,90°],如圖4所示,Nf為面片法向量,NZ為其Z向分量。根據(jù)削弱臺階效應(yīng)的要求,當α接近90°時,在不損失表面質(zhì)量的情況下可適當增加層厚。α越小,越需要細化分層。選用cosα作為分層依據(jù),得到自適應(yīng)分層厚度為

(1)

由三角面片的法向量可以得到夾角α為

(2)

將式(2)代入式(1)可得由面片法向量計算分層厚度的公式,又因STL模型中每個三角形面片的法向量都是單位向量,由圖4的幾何關(guān)系可將式(1)化簡為

(3)

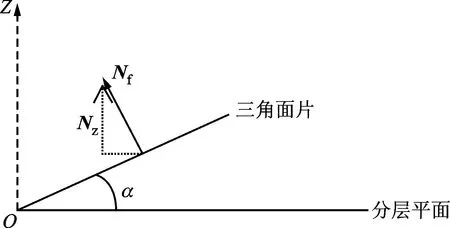
圖4 三角面片與分層平面位置關(guān)系示意圖Fig.4 Schematic diagram of the position relationship between triangular facet and layered plane

2.2 模型特征處識別與保留的分層算法

除臺階效應(yīng)會影響三維打印精度外,模型中還存在一些微小特征處,包括銳邊和復(fù)雜點。如圖5所示,銳邊和復(fù)雜點所在的三角面片傾斜角度接近90°,臺階效應(yīng)并不明顯,所以按照減小臺階效應(yīng)的自適應(yīng)分層算法并不能減小分層厚度。但實際上,若采用較大的層厚,容易產(chǎn)生模型特征的缺失或者畸變[28-29],因此也需要細化分層來保留模型特征。

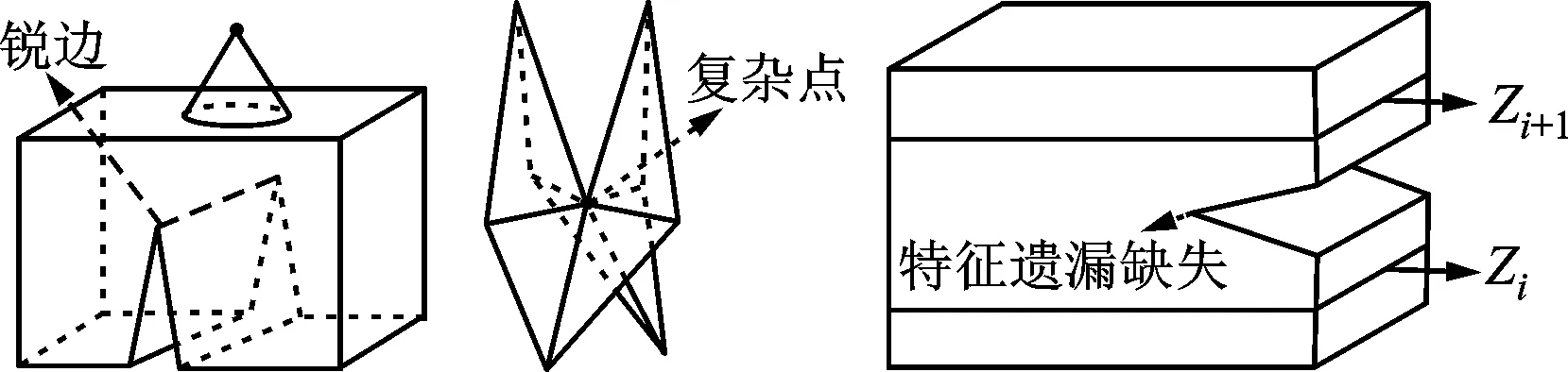
圖5 模型特征示意圖Fig.5 Schematic diagram of model features

二面角可以作為判斷銳邊的依據(jù),其大小能夠反映模型三角網(wǎng)格邊的光滑程度。如圖6所示,F1與F2是STL模型中相鄰的兩個三角面片,其法向量分別是單位向量Nf1與Nf2。三角面片F(xiàn)1與F2的二面角β等于Nf1與Nf2夾角的補角,取值為(0°,180°]。計算公式為

β=π-arccos(Nf1·Nf2)

(4)

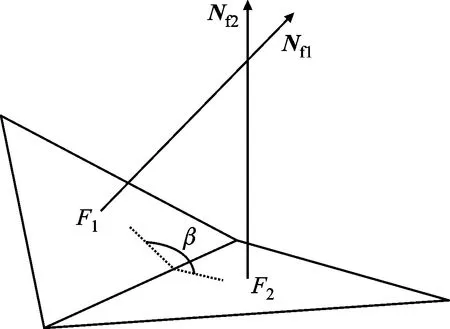
圖6 二面角示意圖Fig.6 Schematic diagram of dihedral angle

二面角越大表明兩個三角面片之間的過渡越平緩。如果某兩個三角面片之間的二面角小于一定閾值,則說明這兩個面片的公共邊為銳邊[30],需要細化分層。選用cosβ作為分層依據(jù),得到自適應(yīng)分層厚度

(5)

模型的另一個特征是復(fù)雜點。可以通過對STL模型的擬合,計算出曲率較大的地方并確定為復(fù)雜點。但實際曲率計算復(fù)雜,算法實現(xiàn)起來較為困難。本文采用一種基于法向量的可反映頂點復(fù)雜程度的指標進行計算。STL模型中的頂點由多個三角面片相交形成,頂點的法向量可以反映該頂點處的方向情況,如圖7所示,Nd為某頂點的法向量,Fi為該頂點相鄰的所有三角面片。

圖7 頂點法向量示意圖Fig.7 Schematic diagram of vertex normal vector

Taubin頂點法向量是以面積為權(quán)值的相鄰三角面片法向量的加權(quán)平均。實際應(yīng)用表明,該頂點法向量的估算方法既簡單又適用[31]。估算公式為

(6)

在求得頂點法向量后,即得到了該頂點處的平均方向特征。該頂點處的復(fù)雜程度與其所在的每個三角面片法向量和頂點法向量之間的夾角有關(guān),夾角越大,表明該頂點處越復(fù)雜。考慮該頂點處所有三角面片的作用,可用z作為判斷該點復(fù)雜程度的指標,計算公式為

(7)

z可以真實地反映三角面片模型各個頂點處的復(fù)雜程度。z的值越小,模型在該點處越復(fù)雜。自適應(yīng)分層厚度

(8)

2.3 算法流程

圖8為本文的自適應(yīng)分層算法流程圖。具體步驟如下。

圖8 本文自適應(yīng)分層算法流程圖Fig.8 Flow chart of adaptive slicing algorithm in this paper

(1)輸入三維模型在分層方向上的最小值Zmin與最大值Zmax,以及打印層厚范圍dmin、dmax,然后對STL文件進行模型信息提取,建立點表、面表進行數(shù)據(jù)存儲,并進行一些初始化設(shè)置。

(3)計算下一層的分層平面高度Zi+1=Zi+di。

(4)判斷Zi層與Zi+1層之間是否有未被切割的三角面片,并對Zi+1進行修正。為了防止類似于圖5中的模型特征遺漏,需要找出兩層之間未被切割的三角面片。兩層之間未被切割的三角面片應(yīng)滿足ZfmaxZi,其中Zfmax、Zfmin為三角面片在Z軸方向上的最值。以(Zfmin)min作為下一分層的平面高度Zi+1。特別地,受到最小層厚的限制,如果(Zfmin)min與上一層的切面高度Zi之間的距離小于最小層厚dmin,那么在確定下一層切面高度時需采用最小層厚,即Zi+1=Zi+dmin。

(5)判斷分層平面高度是否超過模型高度。若平面高度超過模型高度則分層結(jié)束,否則繼續(xù)循環(huán)確定下一層分層高度。最后輸出每層的分層厚度di(i=0,1,2,…,N)。

3 實驗結(jié)果與分析

以Visual Studio 2015為開發(fā)平臺,在等層厚分層的CuraEngine代碼基礎(chǔ)上,采用C++語言實現(xiàn)上述自適應(yīng)分層算法,將CuraEngine改進為自適應(yīng)切片引擎,輸出三維模型的自適應(yīng)分層Gcode文件。為了驗證本文分層算法的可靠性與有效性,下面將本文提出的自適應(yīng)分層算法分別與普通等層厚分層算法、傳統(tǒng)基于法向量的自適應(yīng)分層算法[15]和考慮模型特征的自適應(yīng)分層算法[23-24]進行對比,并給出相應(yīng)的實驗分析。本文選用尖端高度來度量臺階誤差。尖端高度是指打印成品與STL模型表面的最大距離,計算公式為c=(d|NZ|)max。尖端高度越小,臺階誤差就越小,打印精度就越高。同時使用模型分層數(shù)作為衡量打印效率的指標。分層數(shù)越多,打印越耗時,打印效率越低。

分別對龍貓模型(46 mm×56 mm×84 mm)、錐體模型(98 mm×98 mm×93 mm)、啞鈴模型(79 mm×142 mm×79 mm)以Z軸為正方向進行上述分層實驗,分層結(jié)果如表1～表3所示。

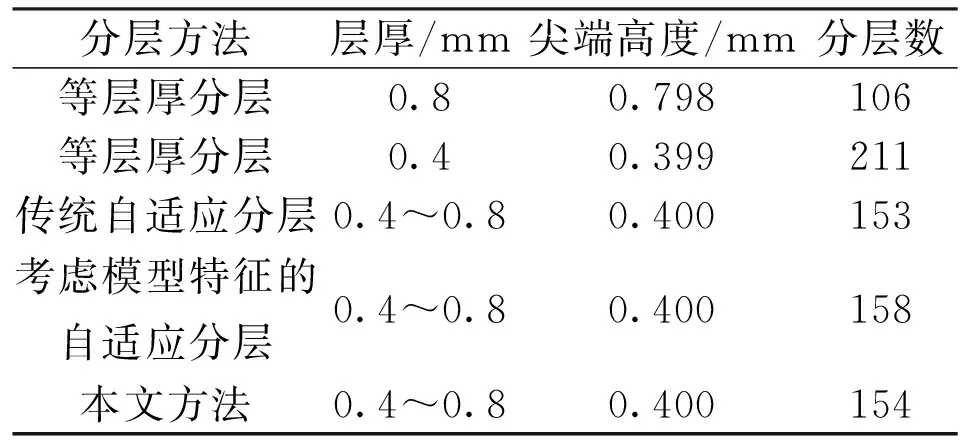
表1 龍貓模型分層結(jié)果對比

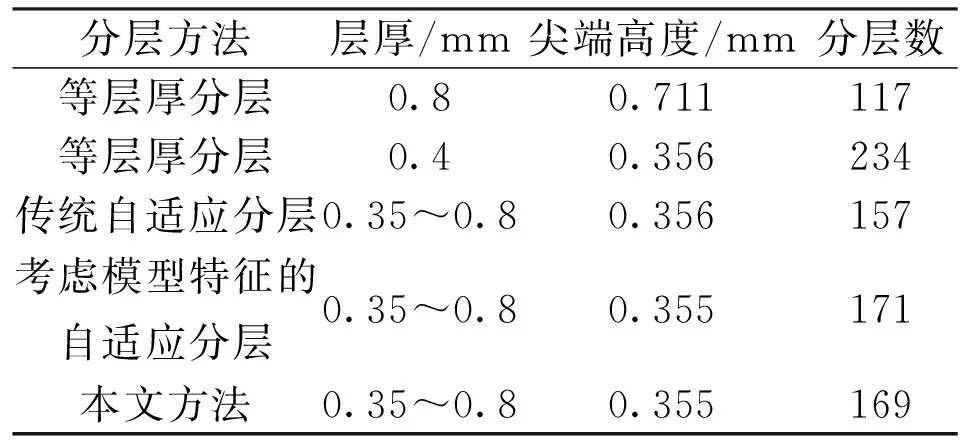
表2 錐體模型分層結(jié)果對比

從表1和表3可以看出,與等層厚分層算法相比,自適應(yīng)分層算法在保證相同尖端高度的同時,可以采用較少的層數(shù),兼顧打印精度與打印效率。為了更明顯地觀察模型特征處保留情況,對以上各類自適應(yīng)分層算法下切片引擎生成的Gcode文件借助Cura軟件模擬打印效果,并用顏色區(qū)分分層厚度,結(jié)果如圖9～圖11所示。

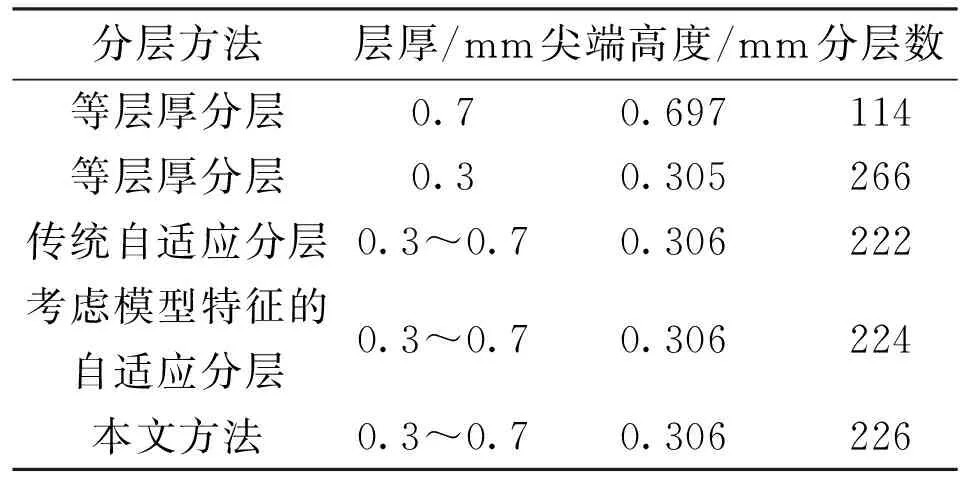
表3 啞鈴模型分層結(jié)果對比

由3個模型的分層效果圖可以看出,與傳統(tǒng)自適應(yīng)分層算法相比,本文算法雖然分層數(shù)有所增加,但是識別和保留模型特征(尤其是微小特征處)的性能較好。相較于考慮模型特征的自適應(yīng)分層算法,本文的自適應(yīng)分層算法具有一定優(yōu)勢:如對于龍貓模型和錐體模型,由表1和表2可知,本文算法的分層層數(shù)較少,分別減少了2.5%和1.2%,是由于該算法可以根據(jù)模型特征的復(fù)雜程度調(diào)節(jié)層厚的大小,能夠盡量使用較小的層數(shù)保留模型特征。而考慮模型特征的自適應(yīng)分層算法是在當模型特征復(fù)雜程度大于一定閾值時均采用最小層厚,不會因為模型特征的復(fù)雜程度而變化。對于啞鈴模型,本文算法的分層數(shù)雖然較多,但卻可以較好地識別并細分模型中部的特征點。一方面,本文算法會對分層過程中遺漏的三角面片進行檢測,防止模型特征遺漏;另一方面,本文算法可以識別任意方向的特征點,而考慮模型特征的自適應(yīng)分層算法只是將模型的局部最高點或者局部最低點作為模型的特征點,無法識別出類似于模型中部的特征點。因此,本文方法具有更好的適應(yīng)性和適用性。

(c)本文自適應(yīng)分層圖9 龍貓模型分層效果圖Fig.9 Slicing effect picture of chinchilla model

(a)傳統(tǒng)自適應(yīng)分層

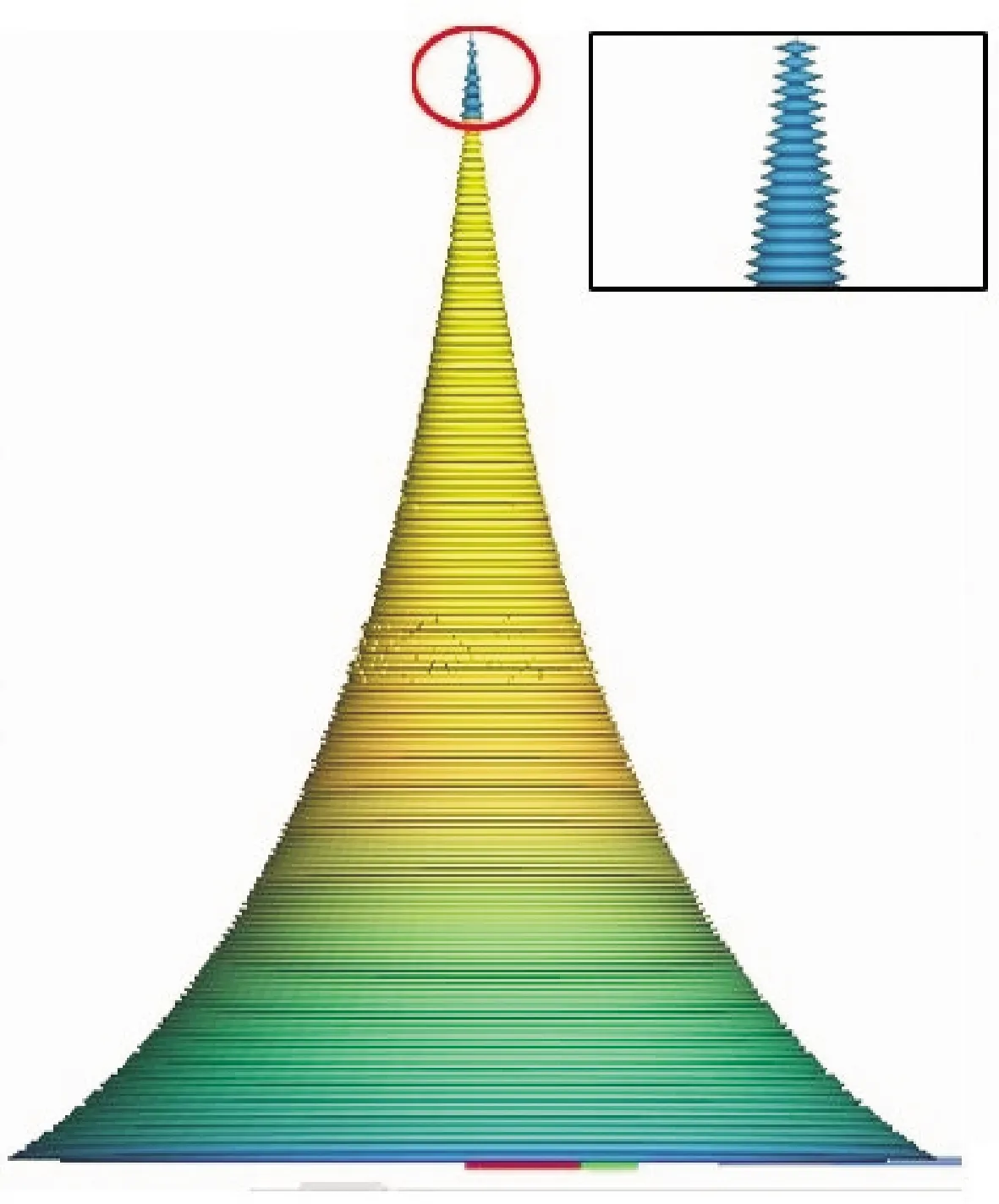
(b)考慮模型特征自適應(yīng)分層

(c)本文自適應(yīng)分層圖10 錐體模型分層效果圖Fig.10 Slicing effect picture of cone model

4 結(jié) 論

(1)本文算法在確定層厚時僅以三角面片法向量為基礎(chǔ)進行計算,方便提取且無需進行復(fù)雜的曲率計算,因此算法的復(fù)雜性較小。

(2)本文算法利用模型面片之間的二面角大小識別銳邊,利用頂點復(fù)雜程度指標識別特征點,能夠識別出傳統(tǒng)算法(如等層厚分層算法、傳統(tǒng)自適應(yīng)分層算法、傳統(tǒng)考慮模型特征的自適應(yīng)分層算法)識別不出的非局部最高或最低特征點等微小特征,因此具有更廣的適用性。

(3)本文算法可以根據(jù)銳邊處二面角的大小和頂點的復(fù)雜程度自動調(diào)節(jié)模型的分層厚度,在保證相同尖端高度和保留特征的前提下,分層層數(shù)相比于傳統(tǒng)算法較少。對于實驗龍貓模型和錐體模型,分層數(shù)分別減少2.5%和1.2%,因此具有更好的適應(yīng)性。

總體來說,本文算法不僅能夠削弱臺階效應(yīng),還可以有效識別和保留模型特征。在高精度3D打印等技術(shù)的分層處理環(huán)節(jié),本文提出的算法針對復(fù)雜模型具有實用性。