伺服系統(tǒng)瞬態(tài)優(yōu)化的模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)方法

魏曉晗,張慶,2,蔣婷婷,梁霖,2

(1.西安交通大學(xué)機(jī)械工程學(xué)院,710049,西安; 2.西安交通大學(xué)現(xiàn)代設(shè)計(jì)及轉(zhuǎn)子軸承系統(tǒng)教育部重點(diǎn)實(shí)驗(yàn)室,710049,西安)

learning; fuzzy control

伺服系統(tǒng)將控制信號轉(zhuǎn)化為精確的機(jī)械運(yùn)動,是機(jī)電裝備向智能化、高精度和高效率發(fā)展的關(guān)鍵基礎(chǔ),也是生產(chǎn)制造數(shù)字化的核心載體。永磁同步電機(jī)(PMSM)具有密度大、幾何尺寸小、重量輕、響應(yīng)快、調(diào)速范圍寬、控制方便等顯著優(yōu)點(diǎn),已成為伺服系統(tǒng)中將電能向可控機(jī)械運(yùn)動轉(zhuǎn)化的最佳選擇之一[1-4]。現(xiàn)代高精度生產(chǎn)線要求伺服系統(tǒng)能夠穩(wěn)定快速地達(dá)到控制目標(biāo),因此以平滑無超調(diào)與快速響應(yīng)為中心的瞬態(tài)響應(yīng)能力成為評價(jià)PMSM伺服系統(tǒng)性能的重要指標(biāo)[5],也成為電機(jī)控制優(yōu)化的研究熱點(diǎn)。

PMSM伺服系統(tǒng)通過對電機(jī)的精確控制實(shí)現(xiàn)高精度加工要求,控制優(yōu)化是目前研究的關(guān)鍵問題。胡強(qiáng)暉等采用全局滑模和變指數(shù)趨近率之間的切換控制,有效地消除了永磁同步電機(jī)伺服系統(tǒng)的抖振現(xiàn)象,但是由于包含大量的超參數(shù),應(yīng)用難度較大[6];吳振順等提出一種模糊自整定PID控制器,對抑制干擾和噪聲有一定的效果,但并沒有考慮瞬態(tài)響應(yīng)速度,整體性能優(yōu)化效果有限[7];蔚永強(qiáng)等采用徑向基神經(jīng)網(wǎng)絡(luò)對系統(tǒng)進(jìn)行自適應(yīng)補(bǔ)償[8],有效地改善了直驅(qū)式伺服系統(tǒng)中穩(wěn)態(tài)跟蹤性能降低的問題,但僅限于仿真研究。由于傳統(tǒng)方法在多目標(biāo)優(yōu)化能力的限制,現(xiàn)階段對于伺服系統(tǒng)的研究仍局限于穩(wěn)態(tài)誤差消除與魯棒性提升,然而對于高精度加工而言,提升系統(tǒng)響應(yīng)速度與抑制超調(diào)同等重要。

作為一種適用于多目標(biāo)優(yōu)化的方法,深度強(qiáng)化學(xué)習(xí)方法搜索能力強(qiáng)、收斂速度快,在控制領(lǐng)域展現(xiàn)出了非常高的應(yīng)用價(jià)值。Pane等結(jié)合Actor-Critic算法以及3D打印機(jī)伺服控制系統(tǒng)提出了一種針對伺服系統(tǒng)的穩(wěn)態(tài)誤差補(bǔ)償方法[9]。陳奇石等針對雙足機(jī)器人穩(wěn)定行走問題,使用有監(jiān)督學(xué)習(xí)中的稀疏在線高斯過程回歸方法對強(qiáng)化學(xué)習(xí)中的函數(shù)進(jìn)行擬合,實(shí)現(xiàn)了雙足機(jī)器人快速、穩(wěn)定行走的步態(tài)規(guī)劃[10]。Han提出了一種基于強(qiáng)化學(xué)習(xí)的在線演化框架來預(yù)先檢測和修改自動駕駛汽車控制器的不完善決策,兼顧了速度與安全性[11]。由于伺服系統(tǒng)瞬態(tài)性能優(yōu)化中存在建模難度高、仿真運(yùn)算量大導(dǎo)致優(yōu)化效率低下的問題,深度強(qiáng)化學(xué)習(xí)尚未應(yīng)用于這一領(lǐng)域。

在強(qiáng)化學(xué)習(xí)中,如何權(quán)衡知識的“探索”與經(jīng)驗(yàn)的“利用”是影響強(qiáng)化學(xué)習(xí)效率與準(zhǔn)確性的重要因素,也是貫穿于強(qiáng)化學(xué)習(xí)發(fā)展史并關(guān)系到應(yīng)用效果的關(guān)鍵性問題。針對這一問題,Schaul等提出了經(jīng)驗(yàn)回放方法[12],即根據(jù)重要性對經(jīng)驗(yàn)池中過往經(jīng)驗(yàn)樣本進(jìn)行采樣。該方法避免了強(qiáng)化學(xué)習(xí)方法中隨機(jī)抽取的弊端,提高了算法的收斂速度和準(zhǔn)確性,但僅限于Q-Learning方式的強(qiáng)化學(xué)習(xí)算法,無法應(yīng)用于采用神經(jīng)網(wǎng)絡(luò)等非線性策略的近似算法。作為經(jīng)典的智能控制方法,模糊控制在強(qiáng)耦合復(fù)雜模型的控制問題中具有良好的技術(shù)優(yōu)勢,通過采用類似優(yōu)先級采樣的策略,有效改善了隨機(jī)性采樣缺陷。因此,通過模糊控制平衡“探索”與“利用”這一對復(fù)雜矛盾,是提高強(qiáng)化學(xué)習(xí)在控制優(yōu)化領(lǐng)域應(yīng)用能力的可行思路。

本文以伺服系統(tǒng)瞬態(tài)性能提升為目標(biāo),提出一種模糊深度強(qiáng)化學(xué)習(xí)算法,利用異步優(yōu)勢演員-評論家強(qiáng)化學(xué)習(xí)算法并行運(yùn)算效率高、收斂速度快、搜索能力強(qiáng)的特點(diǎn),結(jié)合模糊算法在復(fù)雜系統(tǒng)控制中魯棒性強(qiáng)、適應(yīng)性高的優(yōu)勢,建立基于模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)的伺服系統(tǒng)瞬態(tài)性能優(yōu)化方法。基于PMSM伺服系統(tǒng)的仿真計(jì)算模型,優(yōu)化瞬態(tài)性能參數(shù),并將模型計(jì)算參數(shù)應(yīng)用于實(shí)際伺服系統(tǒng)。經(jīng)驗(yàn)證,該方法有效縮短了永磁同步電機(jī)伺服系統(tǒng)調(diào)節(jié)時間,同時抑制了超調(diào)與穩(wěn)態(tài)誤差的產(chǎn)生。

1 問題分析

1.1 永磁同步電機(jī)伺服系統(tǒng)

永磁同步電動機(jī)主要由三相繞組固定定子和永磁體磁極轉(zhuǎn)子組成。當(dāng)三相交流電源供給定子繞組時,產(chǎn)生旋轉(zhuǎn)磁場。旋轉(zhuǎn)磁場與轉(zhuǎn)子上的磁極相互作用產(chǎn)生電磁轉(zhuǎn)矩,激發(fā)轉(zhuǎn)子同步旋轉(zhuǎn)。永磁同步電機(jī)原理如圖1所示。

三相靜止坐標(biāo)系與兩相靜止坐標(biāo)系下的定子磁鏈方程是關(guān)于角度θ的時變方程,為方便控制器設(shè)計(jì),一般在交直軸兩相旋轉(zhuǎn)坐標(biāo)系下對永磁同步電機(jī)進(jìn)行分析。

在交直軸兩相旋轉(zhuǎn)坐標(biāo)系下,伺服電機(jī)交直軸電壓方程為

(1)

式中:ud為直軸電壓;uq為交軸電壓;Rs為定子繞組的電阻;id為直軸電流;iq為交軸電流;Ld為直軸等效電感;Lq為交軸等效電感;ψf為永磁體磁鏈;ω為轉(zhuǎn)子角速度。

本文永磁同步電機(jī)伺服系統(tǒng)矢量控制原理采用id=0控制。在id=0控制方式下,直軸電壓轉(zhuǎn)化為

ud=-ωLqiq

(2)

直軸的電流為0時,不再貢獻(xiàn)轉(zhuǎn)矩電壓。這時電機(jī)的所有的電流全部用來產(chǎn)生電磁轉(zhuǎn)矩,只用需要控制交軸電流iq就可以控制電機(jī)的轉(zhuǎn)矩,從而實(shí)現(xiàn)交直軸電流的靜態(tài)解耦。

1.2 PMSM伺服系統(tǒng)瞬態(tài)響應(yīng)

隨著PMSM伺服系統(tǒng)在工業(yè)生產(chǎn)中的廣泛應(yīng)用,日益增長的高精度生產(chǎn)需求要求其動態(tài)響應(yīng)能力快速提升。作為強(qiáng)耦合系統(tǒng),PMSM伺服電機(jī)與負(fù)載系統(tǒng)的匹配質(zhì)量直接影響電機(jī)啟、停過程中的機(jī)電耦合狀態(tài),從而影響電機(jī)的響應(yīng)能力。在PMSM伺服系統(tǒng)中,存在電動機(jī)驅(qū)動、控制參數(shù)與力學(xué)輸出參數(shù)、電動機(jī)力學(xué)輸出參數(shù)與負(fù)載系統(tǒng)等耦合關(guān)系,其中電機(jī)力學(xué)輸出與負(fù)載耦合方程如下

(3)

(4)

式中:p為電機(jī)極對數(shù);ψd為直軸等效磁鏈;ψq為交軸等效磁鏈;Te為電磁轉(zhuǎn)矩;TL為負(fù)載扭矩;B為阻尼系數(shù);J為轉(zhuǎn)動慣量。

在伺服系統(tǒng)瞬態(tài)響應(yīng)優(yōu)化中,快速性和穩(wěn)定性是控制的核心目標(biāo)。從式(3)(4)可以得出,電機(jī)響應(yīng)的快速性由轉(zhuǎn)子角速度ω及其微分決定,而響應(yīng)的穩(wěn)定性則取決于電機(jī)輸出轉(zhuǎn)矩、角速度及其微分參數(shù)之間的平衡狀態(tài)。因此,實(shí)現(xiàn)伺服電機(jī)動態(tài)性能優(yōu)化,需要從伺服系統(tǒng)中的機(jī)電耦合關(guān)系出發(fā),通過調(diào)節(jié)電動機(jī)的驅(qū)動、控制參數(shù),改變電機(jī)運(yùn)動形態(tài),進(jìn)而影響電動機(jī)力學(xué)輸出參數(shù),從而實(shí)現(xiàn)電動機(jī)在特定載荷下快速性與穩(wěn)定性的平衡,使電機(jī)與負(fù)載系統(tǒng)達(dá)到最佳匹配狀態(tài)。

隨著相關(guān)研究者對PMSM的深入研究,許多對于閉環(huán)控制參數(shù)的優(yōu)化控制方法如滑模變結(jié)構(gòu)控制、模糊控制和自適應(yīng)控制等[13-16],位置的響應(yīng)速度與控制精度得到了顯著的提升。傳統(tǒng)參數(shù)整定尋優(yōu)算法無法兼顧包括響應(yīng)速度和控制精度在內(nèi)的多個控制目標(biāo),或?qū)τ趶?fù)雜耦合問題搜索能力欠佳,因此難以解決伺服系統(tǒng)中復(fù)雜耦合關(guān)系下的驅(qū)動、控制系統(tǒng)參數(shù)優(yōu)化問題。尋求一種適用于多目標(biāo)、多參數(shù)、復(fù)雜耦合問題的控制優(yōu)化方法,是解決永磁同步電機(jī)伺服系統(tǒng)瞬態(tài)性能優(yōu)化問題的關(guān)鍵。

作為一種適用于復(fù)雜控制、決策問題的機(jī)器學(xué)習(xí)算法,深度強(qiáng)化學(xué)習(xí)算法[17-18]在解決多目標(biāo)、多參數(shù)問題中具有收斂效率高,穩(wěn)定性強(qiáng)的優(yōu)勢,使之成為解決PMSM伺服系統(tǒng)瞬態(tài)性能優(yōu)化問題的可行方案。在本文針對伺服系統(tǒng)瞬態(tài)性能優(yōu)化問題,對強(qiáng)化學(xué)習(xí)算法進(jìn)行模糊自適應(yīng)改進(jìn),提高收斂速度以滿足實(shí)際應(yīng)用中時效性的要求。

2 模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)方法

2.1 強(qiáng)化學(xué)習(xí)原理

強(qiáng)化學(xué)習(xí)是一種數(shù)據(jù)驅(qū)動的在線啟發(fā)式機(jī)器學(xué)習(xí)方法,是行為主體從環(huán)境到行為映射的學(xué)習(xí)[19]。作為一種仿生算法[20],在強(qiáng)化學(xué)習(xí)中,智能體通過與環(huán)境交互實(shí)現(xiàn)學(xué)習(xí)過程。智能體從環(huán)境中以狀態(tài)信號的形式接收狀態(tài)信息,并根據(jù)策略函數(shù)π(s,a)采取相應(yīng)的動作。策略函數(shù)π往往是隨機(jī)的,通過與獎勵函數(shù)結(jié)合實(shí)現(xiàn)對每一個可能的狀態(tài)轉(zhuǎn)換的評估,并根據(jù)概率選取動作。在算法的每一步執(zhí)行動作時,環(huán)境將受到動作影響,根據(jù)狀態(tài)轉(zhuǎn)移函數(shù)與獎勵函數(shù)轉(zhuǎn)移到下一個狀態(tài)s′,并得到瞬時獎勵rt。根據(jù)狀態(tài)St計(jì)算得到神經(jīng)網(wǎng)絡(luò)輸出Vt作為本狀態(tài)價(jià)值函數(shù)的估計(jì),由新狀態(tài)St+1更新輸出Vt+1。經(jīng)過N步后完成一個回合的運(yùn)算,并得到回報(bào)函數(shù)Gt。根據(jù)Bellman方程,價(jià)值函數(shù)定義為t時刻狀態(tài)St能獲得的回報(bào)期望,其表達(dá)式如下

Eπ{rt+γVπ(St+1)|St=s}

(5)

式中:γ為折扣因子。

(6)

式中:A(s)為動作空間;p(s′,r|s,a)=Pr{St+1=s′,rt+1=r|St=s,At=a},即在狀態(tài)St=s下實(shí)施動作At=a,得到下一個狀態(tài)St+1=s′與獎勵rt+1=r的概率。

在強(qiáng)化學(xué)習(xí)中,迭代運(yùn)算的目標(biāo)在于訓(xùn)練得到最優(yōu)控制策略π(s,a)最大化累計(jì)獎勵G。以價(jià)值函數(shù)最優(yōu)化為方向進(jìn)行迭代,即可實(shí)現(xiàn)累計(jì)獎勵最大化。

2.2 異步優(yōu)勢演員評論家(A3C)算法

異步優(yōu)勢演員-評論家(A3C)算法是一種基于并行計(jì)算和Actor-Critic算法的深度強(qiáng)化學(xué)習(xí)算法。其中Actor-Critic算法包括Actor和Critic兩個網(wǎng)絡(luò),Actor是一個以策略為基礎(chǔ)的網(wǎng)絡(luò),通過獎懲信息調(diào)節(jié)不同狀態(tài)下采取各種動作的概率;Critic是一個以值為基礎(chǔ)的學(xué)習(xí)網(wǎng)絡(luò),可以計(jì)算每一步的獎懲值。二者相結(jié)合,在不斷迭代中,得到每一個狀態(tài)下選擇每一動作的合理概率。在A3C算法中,創(chuàng)建多個并行的環(huán)境,每個并行環(huán)境同時運(yùn)行Actor與Critic網(wǎng)絡(luò),讓多個擁有副結(jié)構(gòu)的智能體同時在并行環(huán)境上更新主結(jié)構(gòu)中的參數(shù)。并行運(yùn)算中的智能體互不干擾,而全局網(wǎng)絡(luò)的參數(shù)更新則通過每個本地網(wǎng)絡(luò)分別上傳的運(yùn)算后的更新梯度實(shí)現(xiàn),這種更新方式降低了算法中經(jīng)驗(yàn)之間的相關(guān)性,因此收斂性顯著提高。

(7)

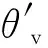
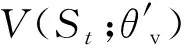
策略函數(shù)π(at|St;θ′)的損失函數(shù)為

cθ′H(π(St;θ))

(8)

式中:cθ′H(π(St;θ))為策略π(at|St;θ′)的熵項(xiàng);價(jià)值函數(shù)的損失函數(shù)為

(9)

對參數(shù)進(jìn)行梯度更新時,Actor網(wǎng)絡(luò)和Critic網(wǎng)絡(luò)采取的策略分別為

cθ′H(π(St;θ))

(10)

(11)

根據(jù)該更新策略迭代后輸出最終的動作結(jié)果。

2.3 模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)算法

在工業(yè)應(yīng)用中,伺服系統(tǒng)由于工況復(fù)雜多變以及在壽命周期中的狀態(tài)變化等問題,優(yōu)化控制時需要考慮實(shí)時性需求,對強(qiáng)化學(xué)習(xí)算法的計(jì)算效率提出了更高的要求,因此必須對強(qiáng)化學(xué)習(xí)中的“探索”與“利用”機(jī)制進(jìn)行綜合平衡。參考生物對于經(jīng)驗(yàn)的記憶程度的區(qū)別,采用的改進(jìn)策略為:區(qū)分經(jīng)驗(yàn)的優(yōu)先級重要性,并根據(jù)經(jīng)驗(yàn)的優(yōu)先級對經(jīng)驗(yàn)區(qū)別記憶。

針對包括Q-Learning在內(nèi)的所有強(qiáng)化學(xué)習(xí)算法,區(qū)分經(jīng)驗(yàn)重要性并實(shí)現(xiàn)記憶區(qū)分的一種可行思路為:通過經(jīng)驗(yàn)中動作得到的獎勵來區(qū)分經(jīng)驗(yàn)重要性,并根據(jù)重要性調(diào)整學(xué)習(xí)率,從而實(shí)現(xiàn)經(jīng)驗(yàn)記憶的優(yōu)先級更新。這種方法借鑒大腦對于不同記憶的深刻程度的區(qū)別,對于“非同尋常”的經(jīng)驗(yàn)印象更加深刻,而對于“司空見慣”的經(jīng)驗(yàn)則記憶程度較低,能夠保證生物在進(jìn)行正常學(xué)習(xí)的同時保持對異常現(xiàn)象的警覺性,從而使生物獲得的知識更全面。在強(qiáng)化學(xué)習(xí)中,動作獎勵表示智能體所采取動作的優(yōu)劣,而學(xué)習(xí)率影響每條經(jīng)驗(yàn)的更新程度,即記憶程度。相應(yīng)地,對于獲得收益或懲罰較大的經(jīng)驗(yàn)采用較大的學(xué)習(xí)率,對于其他一般經(jīng)驗(yàn)采用較小的學(xué)習(xí)率,以期在提高收斂速度的同時保證準(zhǔn)確性。

為實(shí)現(xiàn)該策略,需要尋找一種行之有效的手段,以得到經(jīng)驗(yàn)優(yōu)先級與記憶深度之間的映射。模糊控制算法[21]自1965年提出以來,廣泛應(yīng)用于工業(yè)控制領(lǐng)域,模糊隸屬度作為多因素影響下的綜合決策評價(jià)函數(shù),在系統(tǒng)性能優(yōu)化方面體現(xiàn)出強(qiáng)大的優(yōu)勢。因此,在強(qiáng)化學(xué)習(xí)過程中建立模糊控制器,解決經(jīng)驗(yàn)優(yōu)先級與記憶深度的平衡問題。針對獎勵偏差及其變化率建立論域[-e,e],通過隸屬度函數(shù)運(yùn)算得到輸入值的模糊語言,在模糊控制規(guī)則的條件語句中搜索對應(yīng)學(xué)習(xí)率控制量的模糊語言,最后對控制量模糊語言進(jìn)行清晰化,從而將推理得到的學(xué)習(xí)率控制量轉(zhuǎn)化為學(xué)習(xí)率輸出。算法流程如圖2所示。

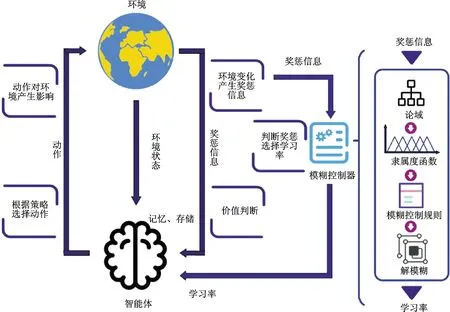
圖2 模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)算法流程Fig.2 Fuzzy adaptive reinforcement learning algorithm flow

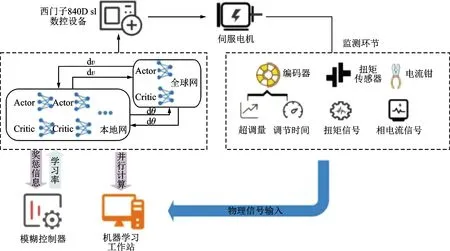
圖3 基于模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)算法的伺服系統(tǒng)瞬態(tài)性能優(yōu)化Fig.3 Transient performance optimization of servo system based on fuzzy adaptive deep reinforcement learning algorithm

3 瞬態(tài)性能優(yōu)化方法

在伺服系統(tǒng)瞬態(tài)性能優(yōu)化中,需要同時考慮響應(yīng)的快速性與穩(wěn)定性兩個方面,使系統(tǒng)響應(yīng)速度得以提升,同時避免演化為欠阻尼系統(tǒng)產(chǎn)生超調(diào)量。針對該問題,基于深度強(qiáng)化學(xué)習(xí)的永磁同步電機(jī)伺服系統(tǒng)瞬態(tài)性能優(yōu)化方法在PID環(huán)節(jié)中設(shè)計(jì)補(bǔ)償環(huán)節(jié),根據(jù)縮短調(diào)節(jié)時間、抑制超調(diào)量的多個控制目標(biāo)建立評價(jià)指標(biāo),利用評價(jià)指標(biāo)設(shè)計(jì)A3C算法獎勵函數(shù),并根據(jù)控制補(bǔ)償環(huán)節(jié)確定A3C算法動作參數(shù),確定最優(yōu)補(bǔ)償參數(shù)。

如圖3所示,在機(jī)器學(xué)習(xí)工作站中建立伺服系統(tǒng)仿真模型,并根據(jù)實(shí)際伺服系統(tǒng)參數(shù)及運(yùn)行結(jié)果擬合仿真模型,減小模型與系統(tǒng)偏差;建立A3C強(qiáng)化學(xué)習(xí)算法全局及本地Actor-Critic網(wǎng)絡(luò),根據(jù)縮短調(diào)節(jié)時間、抑制超調(diào)量的控制目標(biāo)建立強(qiáng)化學(xué)習(xí)價(jià)值函數(shù);在A3C強(qiáng)化學(xué)習(xí)算法中引入學(xué)習(xí)率模糊控制器,根據(jù)經(jīng)驗(yàn)優(yōu)先級調(diào)整學(xué)習(xí)率,提高運(yùn)算效率。

3.1 價(jià)值函數(shù)設(shè)計(jì)

瞬態(tài)性能綜合優(yōu)化的目的在于縮短調(diào)節(jié)時間、抑制超調(diào)量,同時保證正常工作效率。因此,建立伺服系統(tǒng)調(diào)節(jié)時間ts、超調(diào)量σ%、效率指標(biāo)η(電流與扭矩有效值之比)3個瞬態(tài)響應(yīng)性能指標(biāo)作為算法評價(jià)指標(biāo)。設(shè)置評價(jià)指標(biāo)向量即狀態(tài)向量

St={σ%,ts,ηs}

(12)

其中

(13)

ts=t′

(14)

(15)

式中:ctp為伺服系統(tǒng)位置時域響應(yīng)最大偏離值;c∞為伺服系統(tǒng)位置時域響應(yīng)終值;t′為伺服系統(tǒng)位置時域響應(yīng)穩(wěn)定至終值98%所用的時間;Trms為伺服系統(tǒng)扭矩時域響應(yīng)有效值;Irms為伺服系統(tǒng)電流時域響應(yīng)有效值。

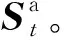
(16)

式中:i1、i2、i3為重要性因子。設(shè)置獎勵函數(shù)和線性補(bǔ)償函數(shù)為

(17)

(18)

式中:Rref為獎勵函數(shù)參考向量;td為補(bǔ)償截止時間。選擇補(bǔ)償放大增益K作為算法輸出動作,作為Actor網(wǎng)絡(luò)的輸出,st和K作為Critic網(wǎng)絡(luò)的輸入。

3.2 Actor-Critic網(wǎng)絡(luò)設(shè)計(jì)

由于徑向基神經(jīng)網(wǎng)絡(luò)逼近精度高、結(jié)構(gòu)簡單、線性擬合,以及便于進(jìn)行微分運(yùn)算的特點(diǎn),在Actor與Critic網(wǎng)絡(luò)的參數(shù)化設(shè)計(jì)中采用該網(wǎng)絡(luò)。

根據(jù)輸入狀態(tài)及動作分別設(shè)計(jì)Actor-Critic算法中Actor與Critic參數(shù)化網(wǎng)絡(luò)參數(shù)φ(s),在[0,1]中等間隔設(shè)置神經(jīng)網(wǎng)絡(luò)中心,隨機(jī)配置初始Actor網(wǎng)絡(luò)權(quán)值參數(shù)θ與Critic網(wǎng)絡(luò)權(quán)值參數(shù)ωi。徑向基神經(jīng)網(wǎng)絡(luò)形式如下

(19)

式中:ci為徑向基中心;n為隱含層網(wǎng)絡(luò)節(jié)點(diǎn)數(shù);k為輸入層節(jié)點(diǎn)個數(shù)。

對網(wǎng)絡(luò)參數(shù)ωi進(jìn)行偏導(dǎo)運(yùn)算

(20)

使用徑向基網(wǎng)絡(luò)設(shè)計(jì)的Actor-Critic網(wǎng)絡(luò),在進(jìn)行梯度更新時,能夠快速地通過微分運(yùn)算得到新參數(shù),從而提高計(jì)算效率。運(yùn)行A3C算法迭代至收斂,即可得到伺服系統(tǒng)補(bǔ)償參數(shù)。

3.3 模糊控制器設(shè)計(jì)

模糊控制器的設(shè)計(jì)包括論域劃分、確定模糊集合、隸屬度函數(shù)求解、模糊規(guī)則推理和解模糊等步驟。定義給定的獎勵偏差為本回合本步收益與前N回合平均收益值之差,根據(jù)運(yùn)算經(jīng)驗(yàn),設(shè)定獎勵偏差e、變化率ec及輸出值學(xué)習(xí)率rl的基本論域。輸入量與輸出量所取的模糊子集的論域都為{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},對應(yīng)的模糊語言為{負(fù)大、負(fù)中、負(fù)小、零、正小、正中、正大}。隸屬度函數(shù)選用三角形函數(shù)的形式,三角形隸屬度函數(shù)分布曲線如圖4所示。

圖4 三角形隸屬度函數(shù)分布曲線Fig.4 Triangular membership function distribution curve

三角形隸屬度函數(shù)表達(dá)式如下

(21)

本文基于三角形隸屬度函數(shù)a(u)設(shè)計(jì)輸入與輸出量隸屬度函數(shù)A(u)如圖5所示,圖中{NB,NM,NS,ZO,PS,PM,PB}對應(yīng)模糊語言{負(fù)大、負(fù)中、負(fù)小、零、正小、正中、正大}。

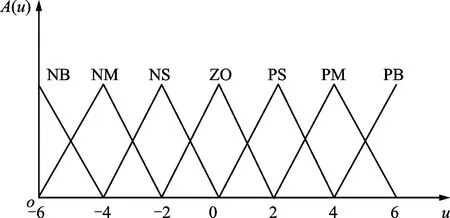
圖5 輸入量與輸出量隸屬度函數(shù)Fig.5 Membership function of input and output

根據(jù)隸屬度函數(shù)可以得到特定獎勵偏差e及其變化率ec對應(yīng)的模糊語言。在進(jìn)行模糊推理時,需要考慮在不同情況下獎勵偏差e及其變化率ec的模糊語言之間的邏輯關(guān)系,并根據(jù)邏輯關(guān)系確定模糊推理結(jié)果。因此,根據(jù)學(xué)習(xí)率整定的工程經(jīng)驗(yàn)建立模糊推理規(guī)則表,如表1所示。

表1 輸出值模糊規(guī)則表

表1中任意一條規(guī)則都可表示為IFeisAi1andecisAi2, THENrlisCi的形式。通過上述的邏輯及條件推理,總共可以將模糊規(guī)則表總結(jié)為49條模糊控制條件語句。

為得到精確輸出值,需要根據(jù)學(xué)習(xí)率的模糊語言,結(jié)合隸屬度函數(shù),通過面積中心法對輸出值進(jìn)行反模糊化。面積中心法表達(dá)式如下

(22)

通過反模糊化,得出學(xué)習(xí)率rl的精確輸出U。

4 仿真實(shí)驗(yàn)

為提高運(yùn)算效率,同時確保系統(tǒng)安全性,本文利用仿真運(yùn)算得到優(yōu)化參數(shù),在仿真模型中驗(yàn)證優(yōu)化效果,繼而應(yīng)用于實(shí)際伺服系統(tǒng)。選擇西門子840D sl數(shù)控系統(tǒng)為實(shí)驗(yàn)對象,包括驅(qū)動器、控制器、執(zhí)行器與檢測器件4個部分,控制參數(shù)如表2所示。

表2 西門子840D sl數(shù)控系統(tǒng)控制參數(shù)

驅(qū)動電機(jī)為西門子1FK7083-2AF71-1AA0永磁同步電機(jī),參數(shù)如表3所示。

表3 永磁同步電機(jī)設(shè)計(jì)參數(shù)

4.1 伺服系統(tǒng)仿真模型

在Simulink仿真環(huán)境中,對PMSM伺服系統(tǒng)建立如圖6所示的仿真模型,包括PID控制器、被控對象、執(zhí)行、檢測、比較、補(bǔ)償6個環(huán)節(jié)。該伺服系統(tǒng)仿真模型采用位置控制方式,主要由通用電橋模塊、永磁同步電機(jī)模塊、空間矢量脈寬調(diào)制模塊、PID控制器、坐標(biāo)變換模塊5個模塊組成,模擬840D sl數(shù)控系統(tǒng)驅(qū)動進(jìn)給軸運(yùn)動過程。

根據(jù)伺服系統(tǒng)電機(jī)硬件參數(shù)與控制參數(shù)配置仿真模型,使模型逼近真實(shí)伺服系統(tǒng)。參照表2及表3,配置圖7所示模型,經(jīng)過仿真運(yùn)算,得到相同行程下伺服系統(tǒng)運(yùn)動軌跡。以600 mm行程為例,軌跡曲線如圖7所示。

實(shí)際伺服系統(tǒng)±5%的調(diào)節(jié)時間為7.06 s,而仿真伺服系統(tǒng)±5%的調(diào)節(jié)時間約為6.47 s,兩者差距為8.49%;實(shí)際伺服系統(tǒng)上升時間約為5.32 s,仿真模型上升時間約為5.02 s,兩者之間差距為5.97%。本文所用到的仿真模型為簡化模型,而西門子840D sl系統(tǒng)中存在復(fù)雜的驅(qū)動參數(shù)與通道控制參數(shù),這導(dǎo)致伺服系統(tǒng)實(shí)際運(yùn)行相應(yīng)曲線與仿真曲線形狀上略有差異,但從瞬態(tài)響應(yīng)性能方面可以認(rèn)為二者性能相近,符合實(shí)驗(yàn)要求。

4.2 結(jié)果及分析

進(jìn)行仿真運(yùn)算,加入模糊控制器后算法在大約第53回合收斂,最大獎勵值為13.58,而未加入模糊控制器時算法大約在152回合收斂,最大獎勵值為13.53。這表明,在加入學(xué)習(xí)率模糊控制器后,收斂準(zhǔn)確性未受影響,而收斂速度得到提升。迭代過程中獎勵函數(shù)變化與未加入模糊控制器變化表現(xiàn)對比如圖8所示。

圖6 永磁同步電機(jī)伺服系統(tǒng)Simulink仿真模型Fig.6 Simulink simulation model of permanent magnet synchronous motor servo system

圖7 仿真模型與伺服系統(tǒng)響應(yīng)曲線對比Fig.7 Comparison of simulation model with servo system response

圖8 優(yōu)化仿真獎勵函數(shù)變化過程對比Fig.8 Comparison of reward function change process in simulation

經(jīng)過運(yùn)算得到最優(yōu)補(bǔ)償增益K=53.564 5,加入補(bǔ)償增益得到仿真補(bǔ)償運(yùn)行結(jié)果與原始運(yùn)行結(jié)果對比如圖9所示。根據(jù)響應(yīng)曲線可以得出仿真前后主要響應(yīng)指標(biāo)如表4所示,補(bǔ)償前的伺服系統(tǒng)調(diào)節(jié)時間為5.02 s,超調(diào)量為0;補(bǔ)償后的調(diào)節(jié)時間為4.13 s,超調(diào)量約為0.3%。在未引入明顯超調(diào)的前提下,調(diào)節(jié)時間縮短17.72%。

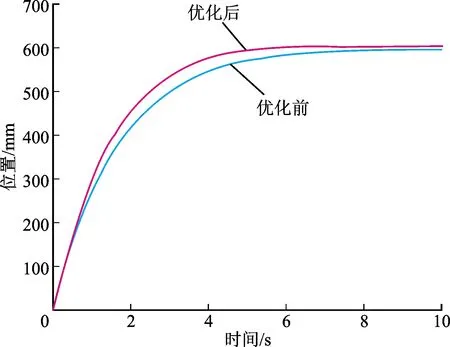
圖9 仿真模型優(yōu)化效果對比Fig.9 Comparison of simulation model optimization effects

表4 仿真系統(tǒng)優(yōu)化瞬態(tài)響應(yīng)指標(biāo)對比

由仿真結(jié)果可知,模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)伺服系統(tǒng)瞬態(tài)優(yōu)化方法可以成功提高系統(tǒng)響應(yīng)速度,伺服系統(tǒng)的調(diào)節(jié)時間和效率都有不同程度的提升。加入模糊控制器,在未影響算法準(zhǔn)確性的同時,大幅提升了運(yùn)算效率。

4.3 系統(tǒng)應(yīng)用

實(shí)際系統(tǒng)如圖10所示,包括SINAMICS S120驅(qū)動系統(tǒng)、SIMATIC S7-300 PLC 控制系統(tǒng)與HMI人機(jī)交互系統(tǒng),負(fù)載裝置選用三菱ZKB-XN磁粉制動器。

圖10 西門子840D sl數(shù)控系統(tǒng)試驗(yàn)臺Fig.10 Siemens 840D sl CNC system test bench

將仿真實(shí)驗(yàn)得到的優(yōu)化參數(shù)輸入實(shí)際數(shù)控系統(tǒng)中,運(yùn)行數(shù)控伺服系統(tǒng)后得到補(bǔ)償前后伺服系統(tǒng)響應(yīng)對比如圖11所示。補(bǔ)償前的調(diào)節(jié)時間為5.32 s,超調(diào)量為0;補(bǔ)償后的調(diào)節(jié)時間為4.75 s,超調(diào)量為0。優(yōu)化后在沒有引入超調(diào)的前提下,系統(tǒng)位置調(diào)節(jié)時間縮短10.71%。優(yōu)化前后響應(yīng)指標(biāo)對比如表5所示。

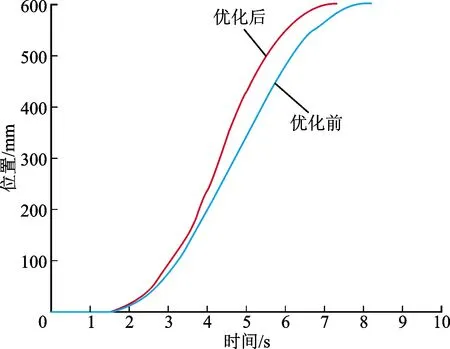
圖11 伺服系統(tǒng)實(shí)驗(yàn)臺優(yōu)化響應(yīng)曲線Fig.11 Effect of servo system optimization

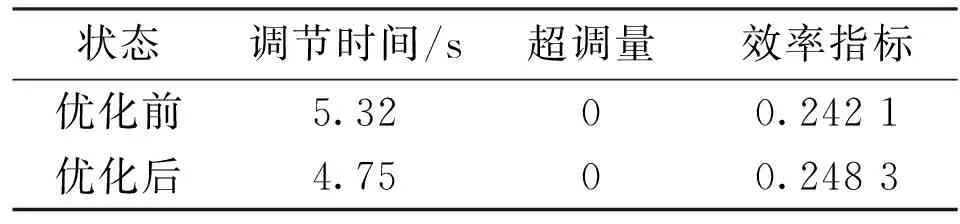
Table 5 Comparison of transient response indexes for optimization of servo system test bench

由實(shí)驗(yàn)可以得出,模糊自適應(yīng)深度強(qiáng)化學(xué)習(xí)方法針對縮短調(diào)節(jié)時間與抑制超調(diào)的多目標(biāo)優(yōu)化問題,明顯提升了實(shí)際伺服系統(tǒng)瞬態(tài)性能。在引入瞬態(tài)性能并行優(yōu)化運(yùn)算得到的優(yōu)化參數(shù)之后,伺服系統(tǒng)的調(diào)節(jié)時間有較大程度的縮短。與此同時,補(bǔ)償優(yōu)化并沒有引入額外穩(wěn)態(tài)誤差,對超調(diào)也有一定的抑制作用,驗(yàn)證了該方法在提升伺服系統(tǒng)瞬態(tài)性能中的有效性。

5 結(jié) 論

通過改進(jìn)深度強(qiáng)化學(xué)習(xí)算法,建立伺服系統(tǒng)瞬態(tài)性能優(yōu)化方法,針對伺服系統(tǒng)特點(diǎn),即運(yùn)行存在時滯性、欠阻尼系統(tǒng)存在超調(diào)的問題,設(shè)計(jì)獎勵函數(shù),利用A3C優(yōu)化算法,得到優(yōu)化補(bǔ)償函數(shù)。結(jié)合伺服系統(tǒng)仿真模型進(jìn)行優(yōu)化仿真,并在西門子數(shù)控系統(tǒng)中驗(yàn)證了優(yōu)化效果。結(jié)果表明,在沒有引入超調(diào)量的前提下對伺服系統(tǒng)的響應(yīng)時間產(chǎn)生了明顯的提升。由于本文方法具有易實(shí)施的特點(diǎn),在優(yōu)化控制領(lǐng)域中將具有良好的發(fā)展?jié)摿Α?/p>