真空柵介質場效應晶體管自熱效應模型

蘇亞麗,賴俊樺,錢俊杰,葉雨欣,張國和

(1.西安石油大學機械工程學院,710065,西安;2.西安交通大學電信學部微電子學院,710049,西安; 3.中國科學院微電子研究所,100029,北京)

受到高功率密度、低熱導率材料、緊湊幾何結構與高表面積與體積比等因素的影響[1-2],溝道內熱量無法及時散出,晶格溫度迅速上升,導致在20 nm及以下工藝節點被廣泛運用的三維立體器件[3-5]環柵硅納米線場效應晶體管(GAA SiNWs FET)存在嚴重的自熱效應,誘發熱載流子注入(HCI)和偏置溫度不穩定性(BTI)等二級物理效應,嚴重威脅器件和電路的性能與可靠性。因此,納米器件自熱效應導致性能衰退的機制和改善熱特性的新器件結構設計成為了近年來研究的重點和難點。

真空柵介質鰭式場效應晶體管(FinFET)是將傳統FinFET[6-8]的固態柵氧化層通過刻蝕工藝去除后所形成一種新型FinFET結構,有效地改善了納米器件HCI和BTI等物理效應[9]。但是,鰭形溝道與底部埋氧層(BOX)存在大面積接觸使得BOX層仍然能夠俘獲高能熱載流子進而影響溝道內電勢分布,導致HCI和BTI等可靠性問題無法從根本上解決。Han等采用懸空硅納米線作為溝道提出了一種氣體環繞的真空柵介質GAA SiNWs FET[10],有效地解決了HCI和BTI對器件性能影響的問題。然而,真空氣體作為柵介質層,其熱導率(0.025 W·m-1·K-1)不足固態柵介質SiO2熱導率(1.4 W·m-1·K-1)的2%,真空柵介質GAA SiNWs FET將具有更明顯的自熱效應。因此,需要深入分析器件內復雜的熱生成與熱擴散過程以揭示真空柵介質GAA SiNWs FET的自熱效應機理。

目前,國內外在數值模擬預測自熱效應引起的納米器件性能衰退的方面進行了大量的研究[11],但是,在這些數值模擬研究中尚未見采用硅納米線熱導率解析模型用于修正三維納米器件的熱電數值模擬仿真模型。硅納米線熱導率存在嚴重的尺度效應和溫度依賴關系[12],采用與溫度和尺寸無關的熱導率模型,如Park和Chung等在3D V-NAND flash存儲器自熱效應分析[13]和FinFET熱SPICE建模研究[14]中采用的常數熱導率,已無法衡量微納尺度材料熱輸運能力[15]。這將導致所建立的數值模擬模型在結構參數設計優化過程中無法準確表征尺寸和溫度變化給熱傳輸性能帶來的影響,在納米器件熱傳輸特性預測中造成較大誤差。

本文將通過考慮溫度與結構尺寸對熱導率的影響,量化表達聲子散色平均自由程與截面尺寸的依賴關系,建立起硅納米線溝道的熱導率模型。通過對真空柵介質GAA SiNW FET自熱效應數值模擬分析,揭示器件內復雜的熱生成與熱擴散機制,探討真空柵介質導熱間隙與氣體壓強對納米器件熱傳輸運能力的影響,為發展真空柵介質器件自熱效應抑制方法和模型預測理論奠定基礎。

1 器件結構與關鍵參數設定

圖1為垂直堆疊GAA SiNWs FET器件結構示意圖,GAA SiNWs FET器件三維結構、YZ截面和俯視圖分別如圖1a、1b和1c所示,其中X軸平行溝道方向,Y軸水平垂直溝道方向,Z軸豎直垂直溝道方向。器件溝道由Ch1、Ch2和Ch3這3根硅納米線垂直堆疊而成。傳統的固態柵介質垂直堆疊GAA SiNWs FET器件一般采用HfO2作為柵氧化層介質。為方便對比分析兩種器件結構散熱能力,本文在保證其他參數不變的情況下,將固態柵介質器件的HfO2柵氧化層替換為氣體材料來構建真空柵介質場效應晶體管的器件結構模型。

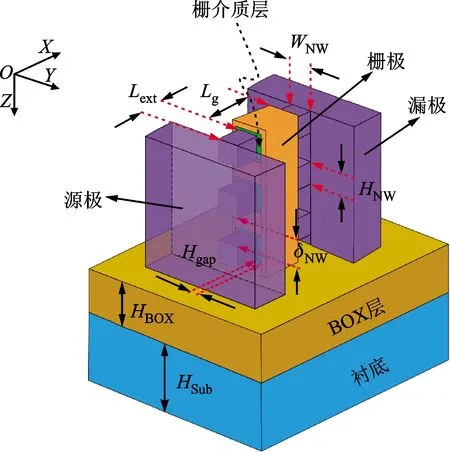
WNW—溝道寬度;HNW—溝道厚度;Lg—溝道長度; Lext—延伸區長度;Hgap—柵介質層厚度;HBOX—埋氧層厚度; HSub—襯底厚度;δNW—納米溝道間距。(a)三維示意圖

(b)截面圖

(c)俯視圖

在TCAD數值模擬仿真中,溝道和源漏分別進行原子濃度為5×1016cm-3的p型本征摻雜和1020cm-3的n型重摻雜。源、柵和漏熱電極表面接觸熱阻為2×10-8m·K·W-1[16]。納米尺度界面熱阻對器件熱傳輸特性有著極為重要的影響,因此在GAA SiNWs FET的高精度自熱效應研究中需要考慮硅/二氧化硅界面熱阻,其大小為9.09×10-9cm2·K·W-1[14]。源漏硅熱導率為62 W·m-1·K-1[17],BOX層二氧化硅熱導率為1.4 W·m-1·K-1。器件尺寸參數為:Lg=40 nm,Lext=25 nm,WNW=4 nm,HNW=4 nm,Hgap=5 nm。

結合器件物理參數與材料電學與熱學特性,考慮納米尺度載流子波動特性與載流子彈道輸運效應,采用密度梯度量子修正模型(Density Gradient Model)、考慮溫度與載流子散射的Philips載流子模型、高電場飽和模型和考慮載流子界面散射的薄層模型,修正TCAD中描述半導體器件行為的基本物理方程,包括,漂移-擴散方程以及熱力學模型等,實現GAA SiNWs FET TCAD熱電數值模擬仿真。

2 硅納米線熱導率模型推導

為在GAA SiNWs FET熱電數值模擬仿真中能夠精確預測器件內溫度場分布與準確評估器件自熱效應,需要建立起可用于器件仿真的溫度和尺寸依賴的、基于物理參數的有源區硅熱導率解析模型。GAA SiNWs FET內聲子平均自由程要遠大于器件有源區尺寸,聲子熱傳輸過程呈現強烈的彈道輸運現象導致經典的傅里葉熱擴散定律已無法揭示納米溝道的熱傳輸機制。通過捕捉影響聲子彈道輸運過程最基本的物理信息,考慮縱向和橫向聲子模對熱導率的貢獻,Holland提出了熱導率的修正模型[18]。將聲子弛豫時間、聲子運動速度和材料尺寸等與聲子彈道輸運緊密相關的物理量包含于材料熱導率模型,表示如下

(1)

式中:下標i=L,T,TU分別表示為單個縱向聲子模態和兩個橫向聲子模態;Θ為德拜溫度;T為材料溫度;vi為不同聲子模態對應的聲子速度;CV,i(T)為溫度依賴的比熱容;τi(T,NA)為溫度T和摻雜濃度NA依賴的聲子弛豫時間;η是考慮聲子邊界散射后用于修正聲子弛豫時間的系數,該參數和材料特征尺寸與聲子平均自由程的比值(H/ι)相關;χ=hω/(2πkBT)是聲子振動頻率,其中h和ω分別是普朗克常量和聲子振動角頻率。

Holland熱導率模型過于復雜,難以植入TCAD軟件以進行三維電熱耦合數值模擬分析,因而針對立方晶體結構硅材料,本文引入聲子平均速度進一步簡化熱導率模型,其表示如下

(2)

從式(2)可以看出,通過近似之后,Holland模型的熱導率與聲子弛豫時間、材料尺寸與熱容呈正比關系。考慮熱傳輸的尺度效應,通過η(H/ι)系數修正聲子弛豫時間,結合已有的體硅材料熱導率模型,即可建立起微納尺度硅熱導率模型。Vasileska等對體硅材料熱導率模型進行了深入的研究與探討[19],結果表明在250～1 000 K寬溫度范圍內硅熱導率的溫度依賴關系可以表示為

(3)

式中:a=0.03;b=1.56×10-3K-1;c=1.65×10-6K-2。因此,立方晶體結構的微尺度單晶硅熱導率模型可以簡單方便的表示成體硅熱導率與衰減因子的乘積形式,表達式如下

λ=λBulkη

(4)

納米硅薄膜平面內尺寸要遠大于垂直平面內厚度,揭示納米硅薄膜傳熱機制是納米全耗盡絕緣體上硅MOSFET自熱效應研究的基礎。硅薄膜厚度對聲子散射的限制占據主導地位,熱導率呈現出很強的厚度依賴關系。McGaughey等對厚度依賴的納米硅薄膜熱導率進行了深入的研究,提出基于體硅模型的納米硅薄膜熱導率的修正模型[20]。修正系數ηFM是硅薄膜厚度的函數,表示如下

(5)

式中:ξ=3kBvHFM/(2λBulkΩ)是無量綱長度,其中Ω是晶胞體積,HFM為硅薄膜厚度。此時,納米硅薄膜熱導率模型可以表示為λFM=λBulkηFM。

不同于納米硅薄膜內聲子散射機制,GAA SiNWs FET中聲子散射同時受納米線溝道截面高度與寬度等尺寸的限制,熱導率在厚度限制的基礎上將會進一步降低。為得到適用于修正硅納米線熱導率的修正系數(ηNW),本文通過求解Gray近似下的硅薄膜與硅納米線熱導率修正系數的關系,結合表達式(5)得到硅納米線熱導率的修正系數。在Gray近似下,硅薄膜熱導率的修正系數如下

(6)

硅納米線的熱導率修正系數可表示為

(7)

式中:ιNW_FM為硅納米線中聲子平均聲子自由程;HNW為硅納米的高度;αFM與αNW為擬合參數,αFM=2αNW;ιFM_MFP與ιNW_MFP分別為硅薄膜與硅納米線中平均聲子自由程,可以表示如下

(8)

其中φ0為常數,當聲子傳播方向與邊界平行時φ0=0。結合表達式(6)～(8),可得硅薄膜和硅納米線中的熱導率修正系數關系

(9)

因此,計入截面橫向與縱向尺寸限制的硅納米線熱導率模型可利用納米硅薄膜的修正系數得到,表示如下

(10)

3 結果與討論

圖2給出了量子效應修正模型下的特征尺寸為40 nm與5 nm的GAA SiNWs FET輸出特性曲線。由圖2可見,短柵與長柵器件都具有較好的性能,但是短溝道效應使得5 nm器件關態電流上升了2個數量級。40 nm器件的等效氧化層厚度(EOT,用符號tEOT表示)為5 nm,5 nm器件EOT為0.6 nm。本文為了更好地研究真空柵間隙對真空柵介質環柵納米線場效應晶體管自熱效應的影響,選用EOT更厚的40 nm器件作為本文的基準參考器件。

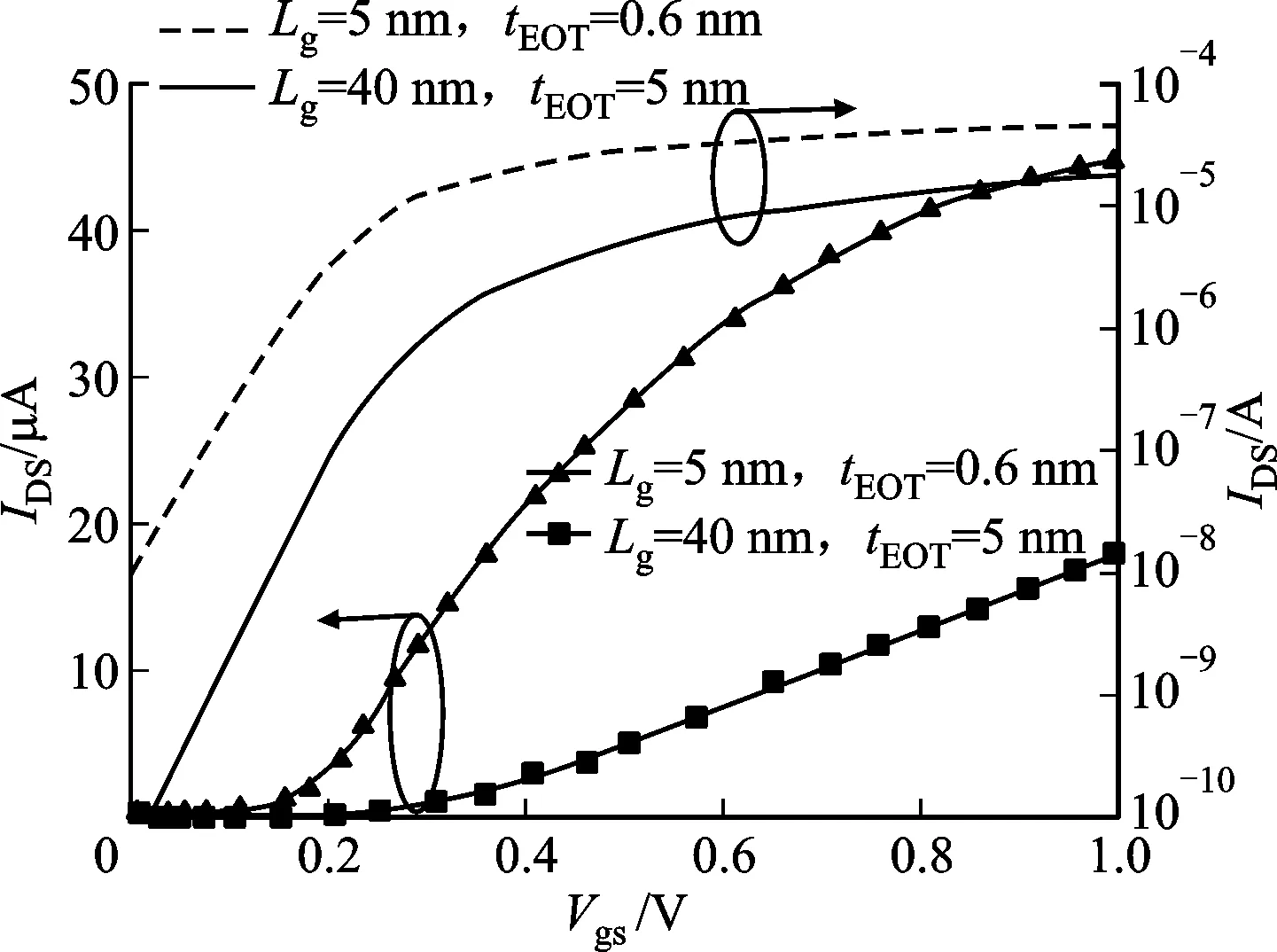
圖2 5 nm與40 nm GAA SiNWs FETs器件輸出特性曲線Fig2 Output characteristics of 5-nm and 40-nm GAA SiNWs FETs

圖3所示為納米硅薄膜與硅納米線熱導率相對于薄膜厚度(用符號HF表示)與納米線寬度的變化關系。McGaughey等在工作中只給出了硅薄膜熱導率的解析模型[17],而對于硅納米線只給出了數值解。從圖3中可以看出,本文所提出的硅納米線熱導率解析模型與McGaughey所計算的數值模型結果吻合得很好。本文模型通過納米尺度下彈道輸運過程的硅納米線與納米硅薄膜之間的自由程近似關系得到硅納米線熱導率,當特征尺寸大于100 nm時,聲子彈道輸運過程將會減弱,模型中的彈道輸運過程自由程的近似在大尺寸下將會產生一定的偏差。隨著硅尺寸不斷減小,硅熱導率由于急劇增加的聲子邊界散射而不斷的降低。同樣是10 nm的尺寸,硅薄膜熱導率將衰減至體硅材料的20%。硅納米線由于聲子散射同時受截面內兩個維度尺寸的限制,熱導率進一步降低至體硅材料的10%。可見,邊界效應對硅納米線內熱傳導有著重要的影響,要實現對GAA SiNWs FET自熱效應的精確模擬分析,就需要在熱電仿真中考慮器件邊界對溝道熱導率空間限制而產生的尺度效應。

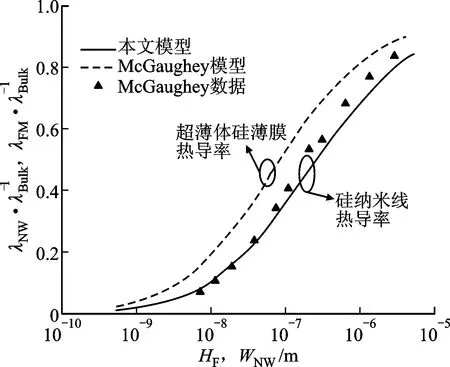
圖3 納米硅薄膜與硅納米線熱導率隨尺寸變化關系Fig.3 Relationships between nanoscale silicon film and SiNW thermal conductivities and size

圖4 固態柵介質GAA SiNW FET漏端延伸區內沿Z軸方向的溫度分布與熱生成Fig.4 Temperature distribution and heat generation along the Z direction in drain extension region of solid gate dielectric GAA SiNW FET

圖4所示為固態柵介質GAA SiNW FET漏端延伸區內沿Z軸方向的溫度分布及熱生成結果。GAA SiNWs FET中3根垂直堆疊納米線溝道Ch1、Ch2、Ch3都存在與之對應的熱生成尖峰,這意味著相比于FinFET等單溝道器件,GAA SiNWs FET有著多個等效熱源。多個熱源的熱量積累分別在納米線溝道中產生了3個溫度極高的熱點。可見,多熱源將會導致GAA SiNWs FET有源區內產生的熱量更容易積聚,使得熱生成與擴散過程變得更加復雜。

沿納米線長度方向的熱傳輸特性決定了GAA SiNWs FET對自熱效應的抑制能力。圖5給出了真空與固態柵介質GAA SiNWs FET納米線溝道熱導率沿長度方向的變化關系。從圖5可知:熱導率隨空間位置的變化而變化;真空柵介質GAA SiNWs FET遭受著更加嚴重的自熱效應,從而導致固態柵介質GAA SiNWs FET硅納米線熱導率在溝道區域整體比真空柵介質GAA SiNWs FET硅納米線熱導率要高。受到溫度和尺寸的雙重限制,沿溝道硅熱導率將從體硅的145 W·m-1·K-1降低至8 W·m-1·K-1。納米尺度下溫度與尺寸效應對硅納米線熱導率的影響不可忽略,只有將熱導率這種依賴關系完整的考慮進數值模擬分析才能夠實現更高精度的納米半導體器件自熱效應分析預測。

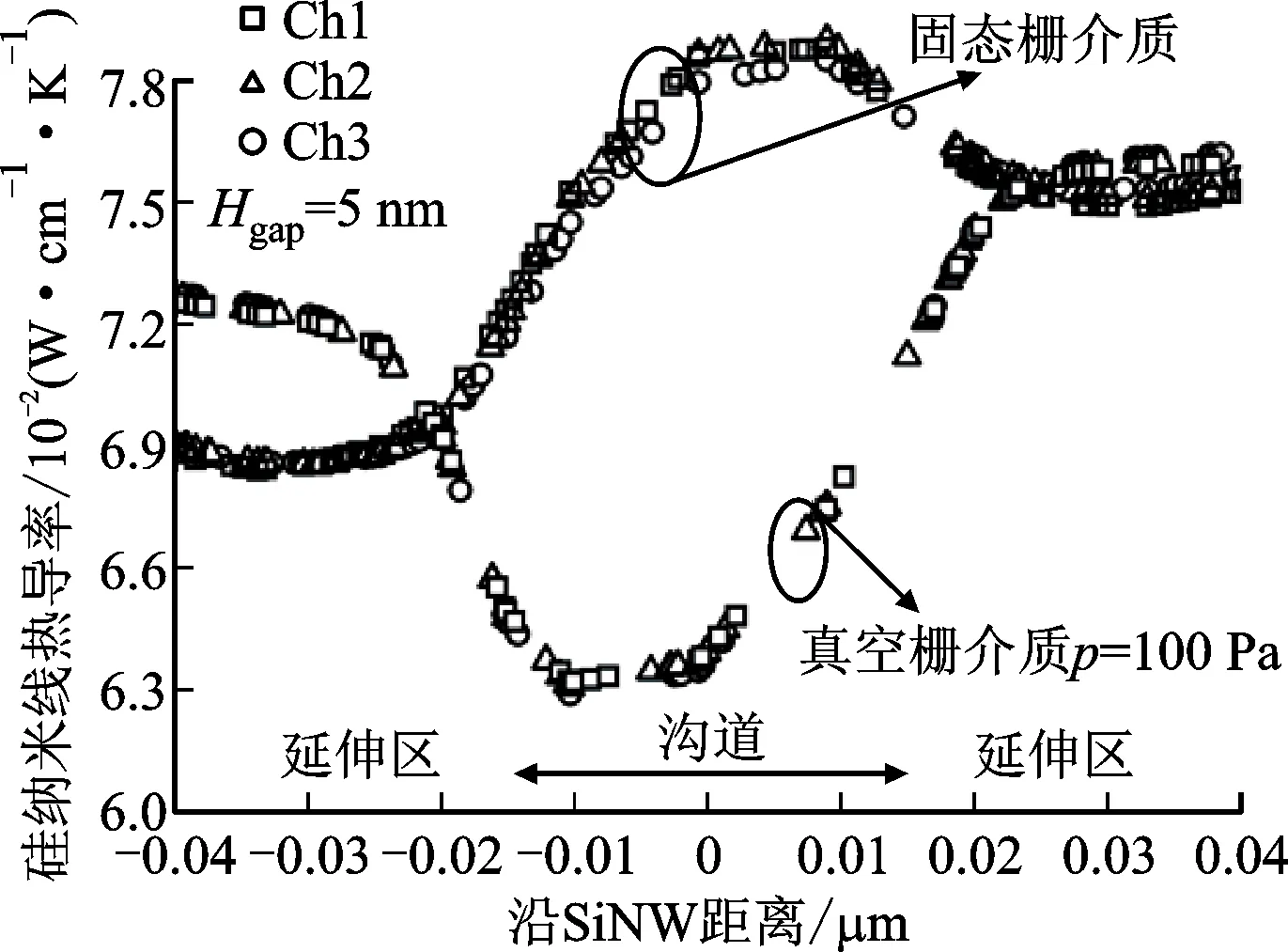
圖5 真空與固態柵介質GAA SiNWs FET納米線溝道熱導率分布Fig.5 Thermal conductivity distribution of SiNW for vacuum and solid gate dielectric GAA SiNW FETs

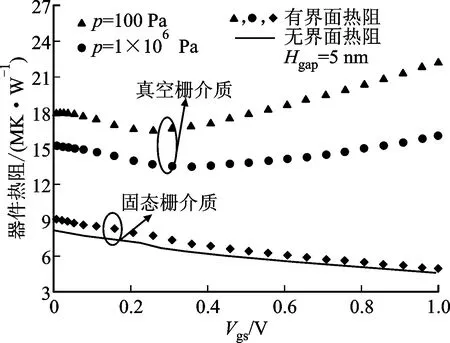
圖6 真空柵介質氣壓和界面熱阻對GAA SiNWs FET自熱效應的影響Fig.6 Influences of gas pressure and interfacial thermal resistance on self-heating effect in GAA SiNWs FET

圖6給出了柵介質種類、氣體壓強和界面熱阻對GAA SiNWs FET自熱效應的影響。圖6結果表明,真空柵介質器件存在更為嚴重的自熱效應,將真空柵介質替換成固態柵介質能夠迅速地降低器件熱阻,在考慮硅/二氧化硅界面熱阻(ITR)后,固態柵介質GAA SiNWs FET的熱阻在柵極和源極偏壓Vgs為0時增加了25%,界面熱阻的引入進一步惡化了器件的自熱效應。隨著Vgs繼續增加,沿著納米線橫向擴散的熱量占總熱量的比重增加,弱化了界面熱阻對器件的作用,最終使得有無界面熱阻2種情況下的器件熱阻趨于相同。真空柵介質的氣體壓強由102Pa增加到106Pa,在柵源偏壓Vgs=1 V偏置時的真空柵介質器件熱阻由2.2×107K·W-1下降至1.6×107K·W-1。這表明一定程度上增加氣體壓強,能夠在不影響器件驅動能力的情況下抑制器件自熱效應。因為增加氣體壓強將提升間隙內氣體熱導率,其表達式如下

(11)

式中:λp0為一個大氣壓下氣體的熱導率;ζ為氮氣的能量調節系數;p表示氣體壓強;Hgap為柵氧化層間隙。納米間隙內氣體分子熱傳輸是彈道熱運輸,因此,不僅壓強會影響氣體熱導率,柵氧化層導熱間隙對氣體熱導率的影響同樣很大。

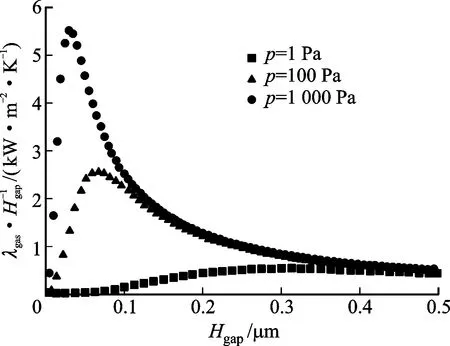
圖7 不同氣壓下柵介質熱導與導熱間隙的關系Fig.7 Relationships between thermal conduction and gap in different gas pressure

圖7所示為在不同氣體壓強下導熱間隙對GAA SiNWs FET柵極熱導的影響。圖7表明:壓強增加使得柵間隙內氣體熱導率增加,真空柵介質層熱導隨之上升;在氣體壓強不變的情況下,隨著Hgap增加,真空柵介質的熱導先增加后減小。這是由于Hgap的增加會增長熱傳輸路徑的同時,也會增加氣體彈道輸運的熱導率,從而使得熱導率不減反增。最大熱導處柵氧化層厚度Hgap與氣體壓強相關,隨著氣壓增加而不斷減小。因此,為了能夠更好的抑制器件自熱效應,需要在器件的工作環境氣壓和柵介質層間隙之間折中考慮。最大化器件的散熱能力,有助于提高器件性能與增強器件可靠性。

圖8給出了導熱間隙Hgap對GAA SiNWs FET整個器件熱傳導能力的影響。從圖8可知:增加導熱間隙Hgap,器件熱阻減小,熱傳輸能力增加;隨著Vgs偏壓由0上升到0.3 V左右,器件熱阻隨著偏壓增加而減小。在低氣壓真空柵介質GAA SiNWs FET中,受柵介質的極低熱導率的影響,熱源產生的熱量主要沿納米線溝道向環境傳輸,納米線熱導率的大小決定了器件的熱傳輸能力。這是由于:Vgs增加使得溝道內電子濃度增加,電-聲子耦合增強了器件的散熱能力,熱阻從而減小;當柵壓偏置進一步增加,GAA SiNWs FET的功率增加,溫度急速上升,硅納米線溝道的熱導率迅速降低,導致器件熱阻反而增加。結合圖6可以更進一步證明,氣體壓強越高,柵氧層熱導率越高,0.3 V之后熱阻上升的趨勢越小,在固體柵氧層中該趨勢消失并反向減小。

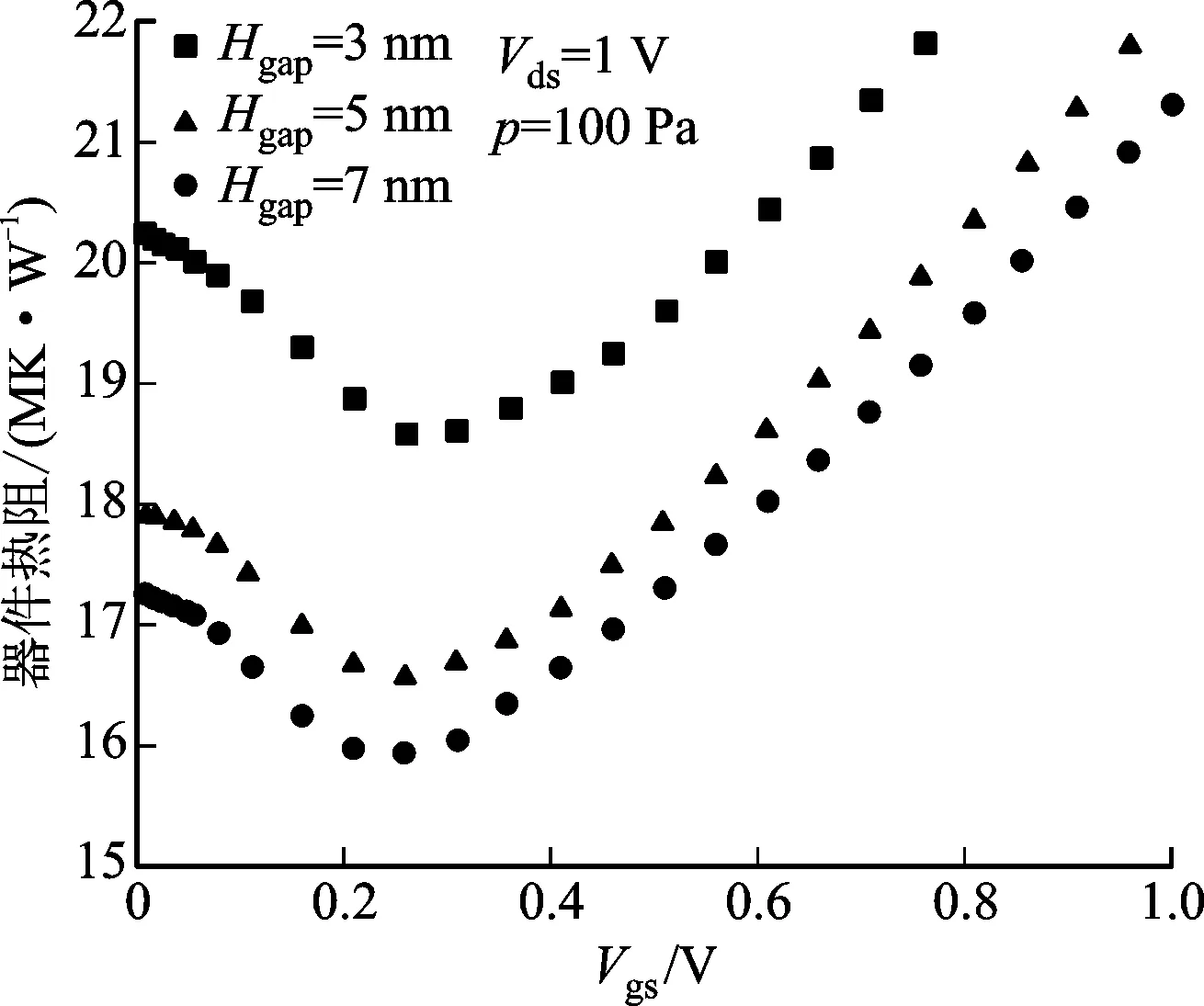
圖8 不同導熱間隙下GAA SiNWs FET熱阻隨Vgs偏置的變化Fig.8 Variation of GAA SiNWs FET thermal resistance with Vgs in different thermal conduction gap

圖9所示為柵、源和漏極接觸熱阻與器件熱阻的關系。由圖9可知:接觸熱阻增加使得GAA SiNWs FET中主要散熱通道熱阻增加,從而導致器件整體熱阻增加;當柵接觸熱阻增加到一定程度時,由熱源向柵接觸的熱擴散通道的熱阻急劇增加并遠大于熱源-源極,熱源-漏極和熱源-襯底等三路散熱路徑的熱阻。此時,器件的熱阻由源、漏和襯底等通道的熱阻決定。繼續增加接觸熱阻,對器件的整體熱阻的貢獻將會很小,器件整體熱阻保持不變。對比發現,增加柵極接觸熱阻導致器件熱阻變化最快。從中可以推測出器件熱源位置距柵極熱接觸最近,器件散熱能力與柵接觸熱阻最為相關。因此,器件熱設計工程師可以通過優化柵極熱接觸結構與材料來降低接觸熱阻,從而達到對GAA SiNWs FET器件自熱效應抑制的效果。

圖9 接觸熱阻與器件熱阻的關系Fig.9 Relationship between contact thermal resistance and device thermal resistance

4 結 論

本文考慮硅納米線截面高度與寬度同時對聲子散射的限制,建立了溫度與尺寸依賴的硅納米線溝道熱導率解析模型,能夠有效評估GAA SiNWs FET中存在的自熱效應。通過對比分析固態柵介質和真空柵介質對GAA SiNWs FET熱傳輸能力的影響,發現真空柵介質器件由于受低熱導率氣體的影響遭受著更加嚴重的自熱效應,器件內熱源位置離柵極區域最近,對柵極材料與結構的熱特性最為敏感。在器件設計時,可以通過折中考慮氣體壓強和柵極介質層間隙距離等參數,采用高熱導率柵材料和設計大面積柵等方法最大化真空柵介質GAA SiNWs FET散熱能力,以達到有效抑制器件自熱效應的目的。