從不定積分的解法來看數學問題解決策略中的整體策略和局部策略

覃秋玲 張桂芳

(廣西壯族自治區南寧市南寧師范大學數學與統計學院 530022)

一、引言

整體策略和局部策略的核心體現在數學解題過程中，可以將求解問題進行拆分，進而把原問題轉化成一些較小或在數學經驗中已經解決過的問題，最后再通過拼湊，使原問題在整體上得到解決的思路.整體與局部在其組成系統的各要素中是相互關聯、相互制約的關系.因此，要在整體中帶有局部意識或在局部中附帶著整體意識去看待數學問題.

二、從不定積分解法看整體策略與局部策略

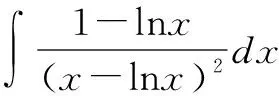
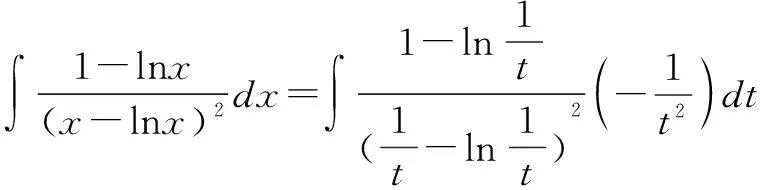
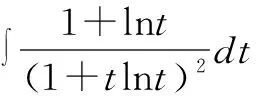
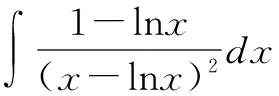
解法一與解法二的相同之處在于充分利用整體與局部策略進行解題，不同在于解法一利用的方法是倒代換法和第一換元法，解法二在進行了簡單化簡之后，對其中的一部分進行分步積分；第二個不同點在于整體與局部策略的應用順序上，解法一是在利用了倒代換法化簡之后才進行，而解法二是直接對原式進行處理.在該題中，對分子的處理方法在中學也很常見，就是熟悉的分拆.“拆與并”是中學數學解題中使用最廣泛的一種裂項并項思想方法.其實，在解數學題時，不僅代數式可拆分，實際上問題也可進行拆分，即將問題中的關鍵結構(式或形)拆分，這里就是對被積函數進行拆分.

而具體問題還得具體分析，在數學問題中，即使面對的是相似題目，有時候雖大體上的思路不變，可細節上的解法卻不同.

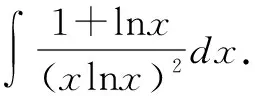
解決此題的關鍵在于從整體和局部觀察被積函數的分子與分母之間的關系，但與上一題的不同在于此題的分母為乘積的形式，因此不采用對分母進行降次的方式，而是利用第一換元法直接解出.此題解法的關鍵d(xlnx)=(1+lnx)dx與上一題解法一的關鍵步驟二d(1+tlnt)=(1+lnt)dt有相似之處，因為d(1+tlnt)=(1+lnt)dt也可看成d(tlnt)=(1+lnt)dt.

下面分析一道較難的例題，觀察整體策略與局部策略在解不定積分中的應用：

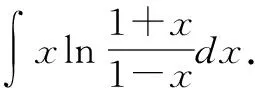
對原式直接進行整體觀察，發現較難進行拼湊，由于被積函數是由兩個不同函數組成，易想到分步積分法，做法如下：

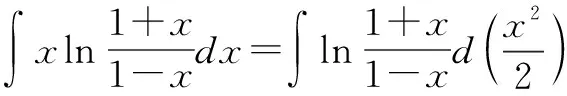
由不定積分的解法來看數學問題解決中的整體策略與局部策略可以發現，整體與局部策略在數學問題解決中是“合作共用”的關系，且需要對具體問題的情形進行具體分析之后方可運用.因解題方法步驟各具特色，所以在解題中，整體與局部策略不能一概而論，有可能是在解題第一步用，也有可能是解題最后一步用；另外就是在解題時需要用整體觀念認識問題，包括問題的條件——已知中的算式結構、圖形的結構、實際意義等，而后居高臨下地把握問題的全局，并從整體結構去理解題意，進而尋求數學問題解決的總體思路.

三、啟示

整體與局部策略還體現在解題時的觀察能力，個體對數學問題越敏感越有助于解題，即數學活動經驗積累的程度.有的式子，往往在把握其整體結構后，才能看出其局部特征以及整體與局部的特殊關系.而不定積分的計算過程本身就復雜，在涉及此類計算時，應當對被積函數進行仔細觀察并簡單嘗試，也更需耐心來選擇解題方法，進而結合整體與局部策略，相信會少走很多彎路！