基于無跡[H∞]濾波的鋰電池SOC估計研究

蘇成龍 羅世昌

摘? 要： 新能源汽車中鋰電池的荷電狀態（SOC）估計是電池管理系統的關鍵技術，對其準確估算有重要意義。所提的算法參考無跡卡爾曼濾波（UKF），將無跡變換（UT）融入到擴展[H∞]濾波中，用以估計鋰電池系統狀態均值和協方差，避免線性誤差累積、增加算法的數值穩定性。在仿真實驗中，在不同動態工況下分析了該算法的估計誤差，證明算法在面對噪聲干擾時具有較好的魯棒性和準確性，是一種有效可行的算法。

關鍵詞： 荷電狀態（SOC）; 鋰電池; [H∞]濾波（HIF）; DP模型

中圖分類號：U469.72? ? ? ? ? 文獻標識碼：A? ? ?文章編號：1006-8228（2021）07-14-04

Research on unscented H-infinity filter based SOC estimation of lithium battery

Su Chenglong， Luo Shichang

（Faculty of Mechanical Engineering & Automation， Zhejiang Sci-Tech University， Hangzhou， Zhejiang 310018， China）

Abstract： State of charge （SOC） estimation of lithium batteries in new energy vehicles is a key technology in battery management system， and it is of great significance to accurately estimate the SOC. The algorithm proposed in this paper refers to the Unscented Kalman Filter （UKF） and integrates the Unscented Transform （UT） into the extended [H∞] filter to estimate the mean value and covariance of the lithium battery system， which avoids the accumulation of linear errors and increases the numerical stability of the algorithm. In the simulation experiment， the estimation error of the proposed algorithm is analyzed under different dynamic conditions. It is proved that the algorithm has good robustness and accuracy in the presence of noise interference， and it is an effective and feasible algorithm.

Key words： state of charge; lithium battery; H-infinity filter; DP model

1 研究背景

隨著社會經濟的不斷發展，由此帶來的能源緊張和環境污染問題將更加突出。在國家科技重大項目和節能與新能源汽車示范推廣等扶持政策的支持和推動下，我國新能源汽車關鍵零部件及相關技術取得重大進步，動力電池發展環境持續優化。動力電池作為電動汽車的核心部件之一，對其關鍵狀態的準確估算和管理是電動汽車發展的核心問題。荷電狀態（SOC）是關鍵狀態之一，對于電動汽車的能源優化管理和生命健康管理具有重要意義。SOC的準確估算可以最大程度地提高動力電池的利用率，延長電池壽命，并最終降低動力電池的成本。

目前常見的SOC估計方法有開路電壓法、安時積分法以及基于模型的方法。開路電壓法需要長時間的靜置，使得電池達到穩定狀態，這顯然不適合實時動態的估計荷電狀態。安時積分法應用最為廣泛，但也存在明顯的缺陷，如其對于初始值準確性高，對于電流傳感器的精度要求也很高，容易產生累計誤差[1]。基于模型估計的方法是目前主流的估計方法，基于模型的估計方法中主要采用擴展卡爾曼濾波算法及其一些衍生算法，例如無跡卡爾曼濾波、容積卡爾曼濾波等[2]。針對鋰電池此類的非線性系統，在線性化過程中不可避免的帶來較大的估計誤差。此外，對于狀態估計中，估計算法也應滿足一定的抗干擾性能。

針對鋰電池狀態估計中存在的不足，本文提出參考無跡變換的方法采用Sigma點傳播的方法進行預測并將其融入[H∞]濾波算法中作狀態估算，將提出的無跡[H∞]濾波簡稱為UHF。

2 鋰電池建模及參數辨識

2.1 鋰電池建模

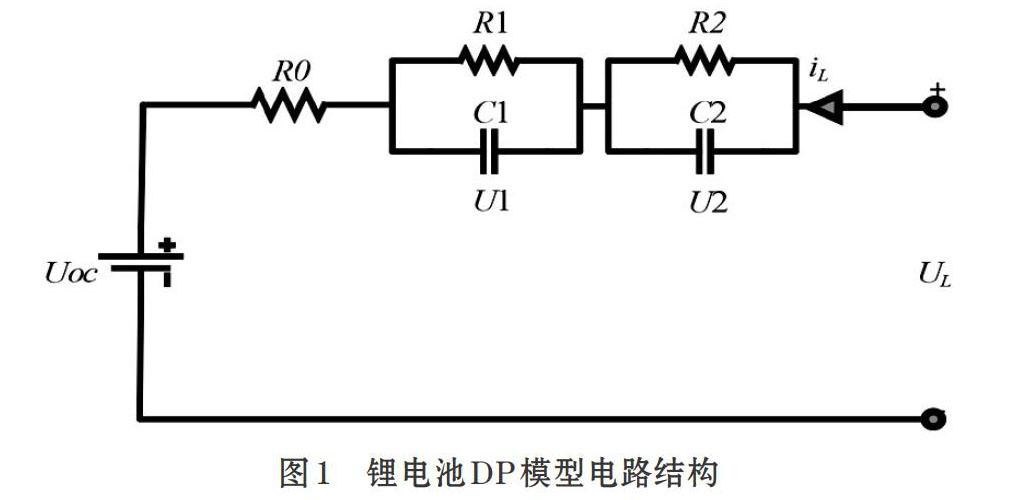
電池管理系統需對儲能系統中鋰電池的多種狀態做出估計和預測，如荷電狀態、健康狀態、內阻等，而實現這些功能的前提是建立精確、可靠的鋰電池模型。常見的電池模型有電化學模型、等效電路模型與分數階模型。為減少多參數帶來的繁重計算，本文采用常見的二階等效電路模型，也稱為雙極化（DP）模型，模型結構如圖1所示。該模型使用電壓源表示鋰電池的平衡電勢，RC網絡描述電池的動力學特性。對動力鋰電池的各種工作狀態有較好的適用性，而且可以推導出模型的狀態方程，便于分析與應用。

根據電路理論，圖1所示的二階RC電池等效電路模型的電學行為可推導為：

[U1.=-1R1C1U1+1C1IbU2.=-1R2C2U2+1C2IbUp=UOCSOC+R0Ib+U1+U2]? ? ⑴

常見的SOC的定義如下：

[SOCt=SOCt0+t0tηItdtCn]? ? ⑵

2.2 電池模型參數辨識

通過測得的數據得到電壓和電流隨時間變化的曲線，根據電壓電流曲線進行參數辨識，得到電池的阻容參數。本文采用HPPC脈沖充放電測試，進行參數辨識。該過程包括多個混合脈沖，以10%SOC間隔放電至放電截止。在每個混合脈沖過程中基于最小二乘原理使用指數擬合法獲得待辨識模型的參數[3-5]。全局優化后的模型參數辨識詳細參數如表1所示。

開路電壓（OCV）與SOC之間的映射關系也是電池的電特性中重要內容。開路電壓參數通過對電池以1C放電10%SOC靜置1h，隨后測量電池開路電壓。重復該放電過程直至電池截止電壓，建立開路電壓OCV與SOC之間的映射關系。本文采用六階多項式擬合實驗值獲取，擬合效果如圖2所示，對應的擬合后的多項式見公式⑶。

[Uoc=11.08×SOC6-25.58×SOC5+17.54×SOC4-1.59×SOC3-2.386×SOC2+1.263×SOC+3.422] ⑶

3 基于UHF的鋰電池SOC估計算法

3.1 系統狀態方程建立

二階RC電池模型的線性狀態方程可表示為：

[xk=Ak-1xk-1+Bk-1uk-1+ωk-1yk=Ckxk+Dkuk+υk]

此處狀態量[xk=U1U2 SOCT];系統矩陣[Ak=1-TsR1C10001-TsR2C20001];輸入矩陣[Bk=TsC1TsC2ηTs3600Cn];

[xk]和[xk-1]分別表示時間步k和k-1的狀態變量，[uk]表示時間步k時刻的輸入電流。[Ts]表示系統的時間步，為簡化計算[Ts]的時間步長設為1s，[Cn]代表電池的額定容量，[η]代表動力電池的庫侖效率。量測方程中

[UL=UOCSOC+U1+U2+R0Ib]，可以推導出[Ck=11?UOCSOC?SOC]，[Dk=R0]。[ωk]、[υk]分別為過程噪聲和量測噪聲，相應的協方差值分別設置為Q和R。

3.2 標準UKF算法

UKF作為經典的濾波算法其也已經被許多研究者應用在鋰電池系統中狀態的估計[6-7]，下面對其計算流程做簡要介紹。

初始化階段對于初值的設置，設置初始狀態量[x0]，相應的均值為[x0]初始協方差為[P0];確定2n+1個Sigma點集對應權重。

⑴ 時間更新

預測Sigma點的狀態：

[x[s]kk-1=fx[s]k-1，uk]? ⑷

通過變換后的Sigma點樣本的線性加權回歸近似計算預測粒子的狀態均值及協方差：

[xkk-1=s=02nωsmxskk-1]? ⑸

[Pkk-1=s=02mωscxskk-1-xkk-1xskk-1-xkk-1T+Q] ⑹

⑵ 量測更新

將Sigma點帶入非線性觀測方程：

[zkk-1=hxskk-1，uk]? ? ⑺

[zkk-1=s=02nω[s]mzkk-1]? ? ? ? ? ? ?⑻

預測新息協方差及互協方差：

[Pzzkk-1=s=02nω[s]czkk-1-zkk-1zkk-1-zkk-1T]? ⑼

[Pxzkk-1=s=02nω[s]cxa[s]kk-1-xkk-1zkk-1-zkk-1T] ⑽

計算增益：

[ Kk=Pxzkk-1Pzzkk-1-1]? ⑾

計算狀態量及其協方差在k時刻的更新：

[xk=xkk-1+ Kkzk-zkk-1]? ⑿

[Pk=Pkk-1-KkPzzkk-1K-1k]? ⒀

3.3 UHF濾波算法

UHF算法對EHF的計算流程做部分更改，下面先對EHF算法原理做簡要說明[8]。EHF詳細推導過程本文不再贅述。

建立如下離散線性系統：

[xk=Akxk-1+Bk-1uk-1+ωk-1yk=Ckxk+Dkuk+υkzk=Lkxk]

上式中：狀態方程與觀測方程不變，增加了估計目標[zk]，[zk]是估計狀態的線性組合;[Lk]為自定義矩陣，依據狀態量中各分量的重要程度進行設計。定義如下代價函數：

[J=k=0N-1zk-zk22x0-x02P-10+k=0N-1（ωk2Q-1k+νk2R-1k）<γ2]

EHF旨在經歸一化輸入噪聲能量和初始誤差能量后盡可能最小化估計誤差能量，即估計目的是最小化[J]的最大值，定義為[minzkmaxωk，νk，x0J<γ2]。由[P-1k=P-1kk-1+HTkR-1Hk-γ-2kI>0]，得[γ2k>maxeigP-1kk-1+HTkR-1Hk-1]，其中[Hk]表示量測模型的雅克比矩陣，max[eigA]表示矩陣A的最大特征值，可得：[γ2k=α maxeigP-1kk-1+HTkR-1Hk-1]，其中，[α]為大于1的尺度參數。

對標準UKF算法流程做部分改動，相應的無跡[H∞]濾波算法如下：

[xk=xkk-1+Pxzkk-1R+Pzzkk-1-1zk-zkk-1]

[Pk=Pkk-1-Pxzkk-1Pkk-1R-1e，kPxzkk-1P[m]kk-1T]

其中：[Re，k=R+Pzzkk-1Pxzkk-1TPzzkk-1-γ2I+Pkk-1]

4 實驗驗證分析

為驗證算法的有效性，測試對象選取主流的三元鋰電池。本次實驗中電芯額定容量為32Ah，標稱電壓為3.7V。本次驗證采用UDDS與DST兩種典型的動態工況驗證SOC估算算法。

兩種典型動態工況下對應的SOC估計結果及誤差如圖3和圖4所示。從圖中可以看出本文所提估算算法誤差整體保持在1.5%左右;即使存在短時間內電流大小甚至方向突變的情況，此時SOC估計誤差也能控制在2%以內。當初值存在10%較大的初值誤差時，算法能在較短的時間內通過迭代收斂到參考值附近并很快穩定到可控的誤差范圍內。由此可見，本文的無跡[H∞]濾波算法有可靠的數值穩定性;在面對較大初值誤差噪聲干擾時具有較好的魯棒性和準確性。

5 結束語

為了改進線性化過程高階項丟失帶來的誤差，本文參考UKF中無跡變換，用無跡變換來處理均值和協方差的非線性傳遞問題。建立了二階等效電路模型，基于最小二乘原理進行參數辨識并進行全局優化，最后在典型動態工況下進行驗證分析。結果表明本文提出的基于UHF估計SOC濾波算法具有2%以內的較小估計誤差且對初值誤差不敏感，是一種有效可行的算法。工程應用中可將算法移植到嵌入式設備中，具有一定的實用價值。后續工作中，將溫度、老化等影響因素加入到算法中，實現對SOC更準確的估計。

參考文獻（References）：

[1] 范興明，曾求勇，張鑫.基于改進安時積分法的電動汽車電池SOC估計與仿真研究[J].電氣應用，2015.34（8）：111-115

[2] 田茂飛，安治國，陳星等.基于在線參數辨識和AEKF的鋰電池SOC估計[J].儲能科學與技術，2019.8（4）：745-750

[3] 羅勇，趙小帥，祁朋偉等.車用動力電池二階RC建模及參數辨識[J].儲能科學與技術，2019.42（4）：125-131

[4] 王伯瑞，鄭培.鋰離子電池SOC估算研究[J].電源技術，2020.44（10）：1506-1509，1517

[5] 陳息坤，孫冬.鋰離子電池建模及其參數辨識方法研究[J].中國電機工程學報，2016.36（22）：6254-6261

[6] 劉潤琴，曾富豪，黃登高.基于RLS和UKF算法的鋰電池SOC估算研究[J].汽車實用技術，2019.12：12-14

[7] 程澤，楊磊，孫幸勉.基于自適應平方根無跡卡爾曼濾波算法的鋰離子電池SOC和SOH估計[J].中國電機工程學報，2018.38（8）：2384-2393

[8] 康國華，劉建業，劉瑞華等.自適應閉環[H∞]濾波在組合導航系統中的實現研究[J].控制理論與應用，2008.3：547-550