管窺高考數學文化題的取材視角
熊康松


【摘要】本文從七個方面結合實例闡述了高考文化數學試題的取材視角.
【關鍵詞】高考;數學文化;取材
數學是人類文化的重要組成部分,對推動社會發展起到重要的作用.數學課程能夠幫助學生形成正確的數學觀.為此,高中數學課程在適當的內容中提出對數學文化的學習要求.近幾年的高考數學試題加強了對數學文化的考查,新課標將數學文化作為課程中的一部分內容,一方面為學生關注數學文化提供“導向”,另一方面使數學試題增添文化色彩與人文氣息.本文從七個方面,展示數學文化試題的取材視角,希望對大家的教學有所幫助.
一、從著名歷史建筑文化古跡中提取素材
歷史文物和古代建筑是歷史的見證,其中蘊含著豐富的文化,以此為素材是高考命題中最常見的一種形式.學生在完成這類試題的過程中,不斷了解和豐富了數學文化知識,增進了民族的自豪感.
例1 某天壇分上、中、下三層,上層中心有一塊圓形石板,環繞它砌9塊扇面形石板構成第一環,向外每環依次增加9塊,下一層的第一環比上一層的最后一環多9塊,向外每環依次也增加9塊,已知每層環數相同,且三層共有扇面形石板3402塊,求下層比中層多塊.
點評 天壇是中國古代祭祀用的場所,有著深厚的歷史特色,本題以天壇為背景命題,考查等差數列的通項公式、前n項和的求法等基本知識.
二、從數學名著中提取素材
從《九章算術》《數學九章》《算法統宗》《四元玉鑒》《詳解九章算術》等古代數學名著中選取素材是很常見的命題方式.
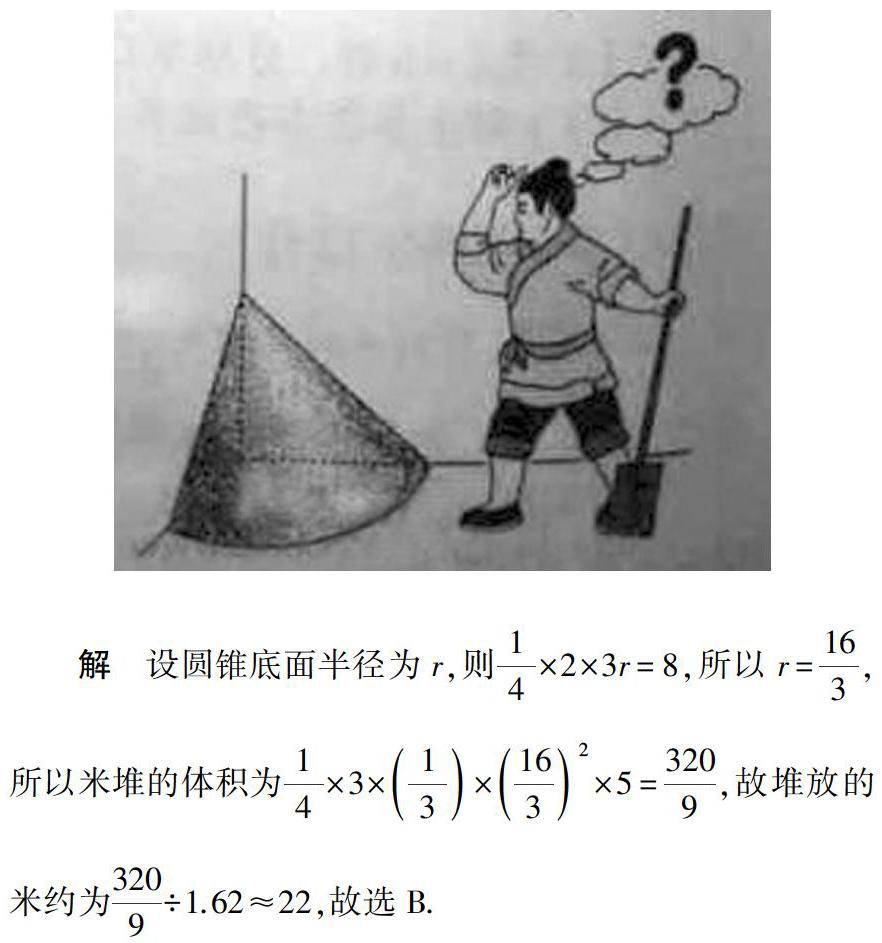
例2 《九章算術》有如下問題:“今有委米依垣內角,下周八尺,高五尺.問積及為米幾何.”其意思為:“在屋內墻角處堆放米(如圖所示,米堆為一個圓錐的四分之一),米堆底部的弧度為8尺,米堆的高為5尺,問米堆的體積和堆放的米各為多少.”已知1斛米的體積約為1.62立方尺,圓周率約為3,估算出堆放的米約有( ).
A.14斛 B.22斛 C.36斛 D.66斛
四、從著名的數學模型中提取素材
在劉徽的《九章算術注》中出現了一些數學模型,如趙爽弦圖、牟合方蓋、陽馬、鱉臑等,以這些數學模型為背景設置數學題比較常見.
五、從著名的數學方法中提取素材
我國古代的一些數學著作中出現了一些方法,如何承天發明的調日法、割圓術等,以這些數學方法為背景設置數學題,新穎別致.
例5 歷史上,求圓周率π的方法有多種,其中數學家阿爾·卡西的方法廣為人知,先計算單位圓的內接正6n邊形的周長和外切正6n邊形的周長,然后讓正整數n充分大,于是將它們的算術平均數作為2π的近似值.按照這種方法,π的近似值的表達式是.
解 單位圓內接正6n邊形的每條邊所對應的圓周角為360°n×6=60°n,每條邊長為2sin 30°n,所以,單位圓的內接正6n邊形的周長為12nsin 30°n,
單位圓的外切正6n邊形的每條邊長為2tan 30°n,其周長為12ntan 30°n,
例6 調日法是古代一種求近似值的方法,已知m,n,h,k∈N,將實數x的過剩近似值和不足近似值分別記為nm和kh,于是x更為精確的過剩近似值或不足近似值為n+km+h,已知π為圓周率,顯然3110<π<4915,分析可知第一次用調日法后得π更為精確的過剩近似值是165,因此有不等關系3110<π<165,假如每次都取最簡分數作為結果,則第三次用調日法后可得π的近似結果為( ).
A.227 B.6320 C.7825 D.10935
解 由調日法運算方法可知,第一次用調日法得π更為精確的過剩近似值是165,即3110<π<165,第二次用調日法后得π更為精確的過剩近似值是4715,即4715<π<165,第三次用調日法后得π更為精確的過剩近似值是6320,即4715<π<6320,故第三次調日法后得到6320為π的近似分數.故選B.
點評 本題取材于我國南北朝數學家何承天發明的調日法,突出對學生運算能力的考查.
六、從著名的數學定理中提取素材
以著名的數學定理(如中國剩余定理、祖暅原理)為文化背景的試題是數學文化類命題的一大熱點.數學定理的內容和推導過程中都蘊含著豐富的數學思想、數學方法和數學文化,這些都將潛移默化地影響學生的思維,激發學生的學習興趣.
例7 祖暅原理為大家熟知的結論大意是夾在兩個平行平面之間的兩個幾何體,若被平行于這兩個平面的任何平面所截,假如截得的兩個截面的面積是相等的,那么這兩個幾何體的體積就會相等.請同學們用祖暅原理解決如下問題:如下圖,有一個倒圓錐形容器,它的軸截面是一個正三角形,在容器內放一個半徑為r的鐵球,再注入水,使水面與球正好相切(而且球與倒圓錐相切效果很好,水不能流到倒圓錐容器底部),然后將球取出,則這時容器中水的深度為.
點評 本題的背景是角谷猜想(也叫敘拉古問題),即對于任意給定的正整數,如果是偶數,就除以2,如果是奇數,就乘以3再加上1,如此運算下去,一定會出現4,2,1的循環.它首先流傳于美國,后來一位名叫角谷的日本數學家將它帶到了亞洲.
很多高考數學文化試題在課本中都能找到,如秦九韶算法、更相減損術、伯努利不等式、阿波羅尼圓、祖暅原理、劉徽割圓術、斐波那契數列等,這些都出現在教材閱讀與思考或探究與發現欄目中,因此教師可以自己改編一些試題,以便學生在學習中使用.

