在疑問中思考 在思考中探究

梁萬里 徐高蓉

【摘要】把一個圓剪拼成和它面積相等的近似長方形，這是通過“化圓為方”思想解決圓的面積問題.僅用“尺規作圖”不能把一個圓化成與它面積相等的正方形.如果不僅僅限于“尺規作圖”，要把一個圓剪拼成和它面積相等的近似正方形，是可以完成的.

【關鍵詞】化圓為方;剪拼;滾動;尺規作圖

【基金項目】本文系2017年度甘肅省“十三五”教育科學規劃課題《小學高段培養學生數學核心素養的課堂教學研究》（課題立項號：GS[2017]GHB0780）的研究成果之一，（本文作者為該課題的負責人）

亞里士多德曾說：“思維自疑問和驚奇開始.”在課堂教學中，常常有許多學生隨機生成的問題引發我們的疑問和思考.

在一次“圓柱的體積”教學研討課上，授課教師給同學們提出了一個問題：“同學們，上學期我們學習了圓的面積，大家回憶一下，圓可以剪拼成哪些和它面積相等的圖形？”同學們踴躍發言，有的說，“圓可以剪拼成和它面積相等的平行四邊形”，有的說，“圓可以剪拼成和它面積相等的長方形”，還有一個同學說，“圓可以剪拼成和它面積相等的正方形”.老師聽完同學們的發言后，說大家回答得都很好，接著就進入了下一個教學環節.聽到最后這名同學的發言，作為聽課老師的我當時一頭霧水，“圓可以剪拼成和它面積相等的正方形嗎？”是授課老師當時沒聽清楚，還是老師不懂數學史知識？對于這么好的課堂隨機生成的資源，老師為什么不進一步追問和評判呢？為了搞清楚這個問題，在課后我問那位授課教師，學生說“圓可以剪拼成和它面積相等的正方形”，你為什么不進一步追問怎么剪呢？怎么不評價呢？她說當時為了趕課，也沒細想，圓是否能剪拼成和它面積相等的正方形，她也不清楚.我又好奇地去問那名學生，你在課堂上說，“圓可以剪拼成和它面積相等的正方形”，圓怎么剪成和它面積相等的正方形呢？你是怎么剪的.我原以為他有辦法，結果在我的一再追問下，他面露為難情緒，說是他隨口說的，他根本不知道怎么剪.可見，在課堂上有時候學生為了表現自己，為了配合老師的教學，活躍課堂氣氛，隨口說出的一句話，引起了我深深地思考.圓到底能否剪拼成和它面積相等的正方形呢？作為老師，我們有必要認真分析研究一下.

首先我們要知道數學史上的一個歷史事實，只用直尺（沒有刻度）和圓規作圖，“化圓為方”是不能完成的，即把一個圓做成與它面積相等的正方形，僅用直尺和圓規作圖是不能夠完成的.這是數學發展史上三個不能用尺規作圖完的著名問題之一，即“化圓為方”問題.另外兩個不能用尺規作圖的問題是“三等分角”問題和“倍立方”問題.“化圓為方”這個著名的數學問題，早在2400年前的古希臘人就已經提出來了，在隨后的幾千年中，無數數學家和數學愛好者苦苦探索，希望能用尺規作圖把一個圓做成和它面積相等的正方形，有的還給出了具體的作圖方法，但到最后都被數學家證明是錯誤的.數學家苦苦探索了幾千年，直到1882年德國數學家林德曼證明π是超越數后，“化圓為方”才被證明為尺規作圖不能完成的問題.

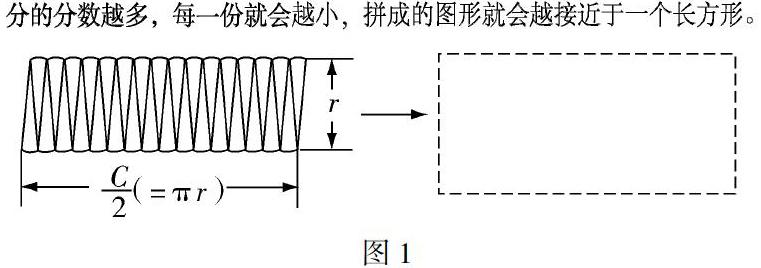
在人民教育出版社編著的新人教版（2013）小學數學教材中，在六年級上冊第五單元講“圓的面積”這一課時，老師讓學生用剪拼法把圓剪成面積相等的小扇形并拼成一個和它面積相等的近似平行四邊形，隨著剪的扇形的份數越來越多，拼成的圖形越來越近似于一個長方形.（如圖1）這個長方形的長近似于圓的周長的一半，等于πr，寬近似于圓的半徑，等于r.因為長方形的面積等于長×寬，所以圓的面積等于πr×r=πr2.這就是小學教材所謂的“化圓為方”，讓學生通過動手操作活動，用剪拼這個方法把圓這個曲邊圖形轉化成直邊圖形，借助圖形直觀，用轉化方法解決了圓的面積問題，滲透了轉化思想和極限思想.而這個“化圓為方”與數學史上的“化圓為方”絕不是同一個概念.

如果按課堂上那名同學的想法我們進一步進行數學推理，假設一個圓能剪拼成一個和它面積相等的正方形，那么就會有πr=r，移項得（π-1）r=0，根據兩個因數乘積為0，必有一個因數為0，要么r=0;要么r≠0，π=1，無論哪種情形都是錯誤的.可見，根據六年級學生的年齡特點和認知水平，說把一個圓剪拼成一個和它面積相等的正方形是沒有經過思考隨口說出的，是經不起追問和推理的.

那么，如果要把一個圓剪拼成和它面積相等的正方形，就沒有辦法了嗎？作為老師，我們要認真研究思考并回答這個問題，把在課堂上出現的疑問認認真真解決好，這樣既能進一步提升教師的專業素養，又能不斷豐富厚實我們的數學史和數學文化知識.我仔細查閱有關資料，經過深入學習研究思考后，發現辦法確實是有的，而且很多，下面我僅提供三種方法供大家思考.

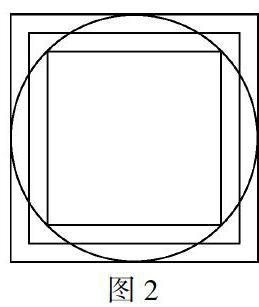
方法一：割補法（如圖2）

這種方法就是在圓的內接正方形和圓的外切正方形的中間找一個正方形，逐漸調整正方形的大小，使它的面積與圓的面積相等.

因為我們知道，一個圓的面積總比它的內接正方形的面積大，總比它的外切正方形的面積小，所以對于圓這種曲邊圖形來說，和這個圓面積相等的正方形只有在圓的內接正方形和外切正方形中間找，這是一種最容易想到的最直接的方法.我們不斷調整正方形的大小，使得圓多出正方形的每一個小弓形的面積恰好等于正方形每一個角多出圓的面積.這樣，把每一個小弓形剪下來割補到正方形每一個角，使得它們的面積恰好相等，這樣圓的面積就等于正方形的面積，我們就完成了把一個圓剪拼成和它面積相等的正方形.

這種方法和中國古代的“出入相補”一樣，經過分割和移補，把圖形多出的面積正好移到需要補的地方，使得多出的面積與補的部分的面積相等，雖然圖形的形狀發生改變但是面積保持不變.這個方法有一個缺點，要想使得圖中正方形多出的每一個弓形的面積恰好等于正方形里面每一個角多出圓的面積，只能通過不斷剪拼與調整，需要重復操作好多次才能完成，并且有一定的誤差.

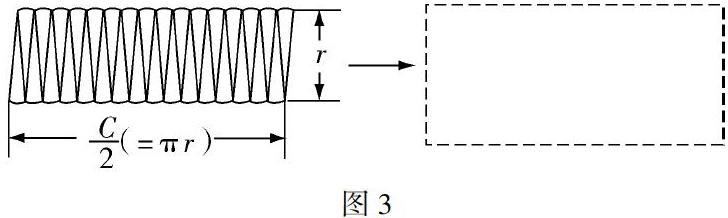
方法二：剪拼法+尺規作圖法（如圖3、4）

這種方法就是按照小學課本上的方法，先把一個圓剪成很小的扇形，再把這些小扇形拼成一個近似長方形，再用尺規作圖把這個長方形做成和它面積相等的近似正方形.

具體做法如下：

1.作線段AD等于長方形的長（πr）;

2.延長AD至E，使DE等于長方形的寬（r）;

3.以AE為直徑作圓;

4.過點D作AE的垂線段交圓于點H，連接AH，EH;

5.以DH為邊作正方形DHGF.

則正方形DHGF為所作的與原來的圓面積相等的近似正方形.

為什么正方形DHGF的面積與原來的圓面積相等呢？其實道理很簡單，只要學過初中的數學知識就能聽懂.因為以AE為直徑作圓，DH垂直于AE，根據直徑所對的圓周角是直角，所以三角形AHE為直角三角形.根據射影定理，DH2=AD×DE，即DH2=πr×r=πr2.以DH為邊作正方形DHGF，說明以DH為邊作的正方形DHGF的面積（DH2）就等于πr2，所以，正方形DHGF的面積與原來的圓面積相等.不過，這個面積相等也是一種近似的相等，因為在開始把圓剪拼成長方形時存在一定的誤差，盡管后面的尺規作圖是嚴格的幾何作圖，但仍然是一種近似的面積相等.

方法三：滾動法+尺規作圖法（如圖5、6）

這種方法就是先滾動直徑為1個單位的圓一圈，做出π，再用尺規作圖法做出正方形.

具體做法如下：

1.作線段AD等于圓滾動一周的長（π）;

2.延長AD至E，使DE等于1[]4個單位長;

3.以AE為直徑作圓;

4.過點D作AE的垂線段交圓于點H，連接AH，EH;

5.以DH為邊作正方形DHGF.

則正方形DHGF為所作的與原來的圓面積相等的近似正方形.

道理與方法二相近.因為以AE為直徑作圓，DH垂直于AE，所以三角形AHE為直角三角形.根據射影定理，DH2=AD×DE，即DH2=π×1[]4=1[]4π.以DH為邊作正方形DHGF，說明以DH為邊作的正方形DHGF的面積（DH2）就等于1[]4π，而直徑為1個單位的圓的面積就是1[]4π，所以，正方形DHGF的面積與原來的圓面積相等.這個面積相等也是一種近似的相等，因為在開始把圓滾動時作π存在一定的誤差，盡管后面的尺規作圖也是嚴格的幾何作圖，但仍然是一種近似的面積相等.

以上三種作圖方法，都可以把一個圓做成和它面積相等的近似正方形，都已經超越了尺規作圖的限制，達到了“化圓為方”的目的.并且后兩種幾何作圖應用了初中的“射影定理”，超出了小學生的認知水平.

把一個圓做成和它面積相等的正方形，是數學史上的著名問題，僅僅使用直尺（沒刻度）和圓規是不能完成的.因為圓周率π是一個無理數，算出圓面積后進行算術平方根運算，最后得到的正方形的邊長仍然是無理數.因為無理數不可能用尺規精確做出它在數軸上所表示的點的，這就是為什么一個圓不能用直尺和圓規做成和它面積相等的正方形的原因.

數學課是最能培養學生思維能力的課，在數學課上出現的與預設不同的隨機生成的問題是一種很好的教學資源，老師要善于捕捉這種資源并利用它為我們的教學服務.作為老師一定要養成善于思考的習慣，在學生有疑問的地方多一些思考，在思考時多一些探究.要挖掘每節課的廣度和深度，既要關注備課的預設，又要考慮課堂上隨機生成的問題，要能在學生的問題中深挖數學知識本質，透過問題把我們的課堂教學進一步引向深入.在課堂上要加強學生的數學思維能力訓練，有效滲透數學思想方法和數學文化知識.只有這樣，我們的課堂教學才能不斷促進學生深度思考，學生的思維品質才能不斷提升，學生的數學核心素養才能真正在課堂落地生根.

【參考文獻】

[1]李文林.數學史概論[M].北京： 高等教育出版社，2000.

[2]董毅.數學思想與數學文化[M].北京：北京師范大學出版集團，2012.