計算教學的新思路

曾娟林

在小學數學教學中，運算能力是小學生必須掌握的最重要的能力之一，是日常生活與進一步學習的重要基礎。下面，筆者以《三位數乘兩位數》一課的教學為例，談一談在計算教學中除了技能訓練，應當如何培養學生的思維能力。

一、巧設練習，強化數感和推理能力的培養

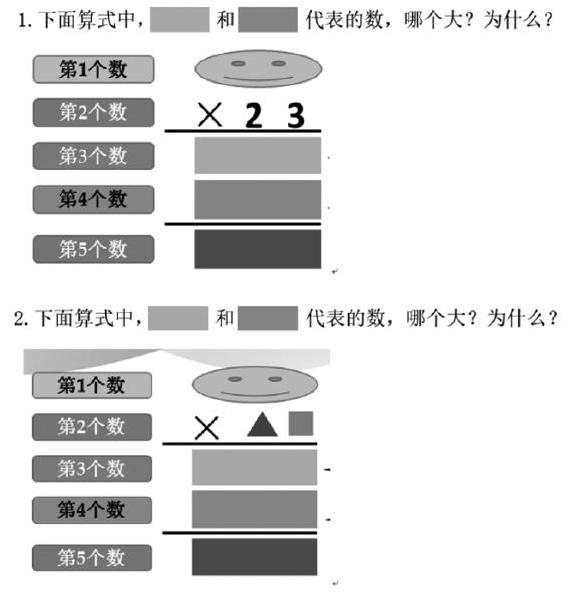
數感是指數與數量、數量關系、運算結果、估計等方面的感與悟。筆者認為，可以通過下面的練習（如圖1-2），來加強數感和推理能力的培養：

判斷綠色方框和藍色方框代表的數，哪個大？這個過程，就是一個推理的過程，也是感悟數的大小的過程。通過這樣的習題，不僅可以鞏固“理法”，還可以培養數感，積累推理的活動經驗。

二、自主探究“理法”，發展遷移能力

（1）復習舊知，為遷移奠基鋪路

以下是《三位數乘兩位數》一課中“引入部分”的教學片斷。

【教學片斷】復習舊知，引入新課

1.計算“6×4= ? ? ? ? ? 16×4=

216×4= ? ? ? 16×14=”

2.說一說16×4是怎么算的？ ?生：從個位起，依次乘。師：216×4呢？生：也是從個位起，依次乘。老師板書：個位起，依次乘。

3.16×14，說一說你們是怎么算的？生：先用4乘16算出4個16，再用十位的1乘16算出10個16，再把兩個積相加。老師板書：分別乘，積相加。

遷移是利用已有的知識經驗或方法解決新的問題，在計算教學中，教師在備課時應找準知識遷移的“基點”。如上面片斷中，三位數乘一位數和兩位數乘兩位數這兩個法則是學生遷移學習三位數乘兩位數的基點。因此，在課始復習舊知時，呈現兩個法則，為遷移奠基鋪路。

（2）自主探究，讓遷移自然發生

【教學片斷】學生復習舊知之后，老師讓學生自主探究、獨立用豎式計算216×14。

雖然沒學過 “三位數乘兩位數”，但有之前的“基點”鋪墊，學生很自然地將前面兩種法則遷移到新問題的解決上。筆者在三所不同層次的學校共6個班實施了教學，6個班的學生，幾乎全部都能自主遷移，用正確的方法計算216×14。這說明了學生們雖然不懂得什么叫遷移，但遷移已經很自然、真實地發生了。

（3）厘清聯系，讓遷移清晰可見

【教學片斷】老師請一位學生在黑板上完成216×14的計算，學生陳述計算方法后，老師提出問題：這種計算我們沒有學過，你是怎么知道要這么算的呢？生：前面的兩位數乘兩位數就是這么算的，216×14和16×14的第二個乘數是一樣的，知識第一個數多了一個數字，所以計算方法都是一樣的，都是分別乘，積相加。老師繼續追問：第一個乘數多了一個數字會有什么不一樣呢？生：就是乘的時候多乘一位。

通過上面片斷的教學，學生們通過找出三位數乘兩位數和兩位數乘兩位數、三位數乘一位數的關系，發現它們的方法一樣，這樣就可以舊知識解決新問題，我們把這種學習方法叫遷移。通過對比，學生可以發現從兩位數乘一位數到三位數乘一位數、從兩位數乘兩位數到三位數乘兩位數、從第二個乘數是一位數到第二個乘數是兩位數，這些都是遷移。老師繼續追問，我們還能用遷移的方法，學會哪些新知識？經過小組討論，學生得出根據兩位數、三位數乘一位數，可以學習四位數乘、五位數乘一位數……進而構建多位數乘一位數的方法。同理，可以得出多位數乘兩位數的方法，再進而得出多位數乘多位數的方法。

此時，老師出示小學數學教材的編排，學生發現學習了三位數乘兩位數之后，課本沒有再安排筆算乘法的學習了。在學生的困惑中，老師再拋出問題：“為什么教材不再安排整數乘法（筆算）的學習內容了？”當學生說出：“因為我們可以通過遷移自己學習！三位數乘三位數都可以算出來了。”之后，其他學生頻頻點頭，甚至躍躍欲試，有的學生還喊出了四位數乘四位數也可以，并準備開始計算……筆者相信，此時此刻，遷移已經在學生的內心生根發芽。

責任編輯 ? ?徐國堅