借助教材例、習(xí)題為學(xué)生搭建數(shù)學(xué)認(rèn)知“小階梯”

楊周榮麟

教材是學(xué)生的學(xué)習(xí)之本，也是教師教學(xué)首先需要研究與討論的主要內(nèi)容.我們知道，教材中每一節(jié)課的例題與習(xí)題設(shè)計(jì)一定都承載著教學(xué)示范功能，是考查學(xué)生學(xué)習(xí)能力、應(yīng)用所學(xué)知識(shí)實(shí)踐的主要載體，也是體現(xiàn)教學(xué)中滲透數(shù)學(xué)學(xué)科培養(yǎng)目標(biāo)與核心素養(yǎng)的主要依據(jù).因此，教師對(duì)每節(jié)課教材配置的例題和習(xí)題都應(yīng)該進(jìn)行認(rèn)真研究，以學(xué)生的具體學(xué)情為基石，借助這些題目為學(xué)生學(xué)習(xí)、應(yīng)用新知搭建認(rèn)知“小階梯”，讓他們快樂地學(xué)習(xí)、積極地獲取.在這里筆者以北師大版《數(shù)學(xué)》九年級(jí)上冊(cè)第四章第七節(jié)“相似三角形的性質(zhì)（第1課時(shí)）”為例談?wù)勅绾谓柚滩睦⒘?xí)題為學(xué)生搭建認(rèn)知“小階梯”.

縱觀第四章，學(xué)生已經(jīng)有了成比例線段、平行線分線段成比例、相似多邊形、相似三角形的定義與三種判定方法的知識(shí)儲(chǔ)備，可以類比幾何學(xué)習(xí)方法進(jìn)行相似三角形性質(zhì)的研究.教材在章節(jié)前明確提出三方面的學(xué)習(xí)目標(biāo)：了解相似三角形的性質(zhì)，進(jìn)一步提高推理能力，并利用圖形的相似解決一些簡(jiǎn)單的實(shí)際問題.因此，在課程設(shè)計(jì)時(shí)，應(yīng)落實(shí)學(xué)習(xí)目標(biāo).第七節(jié)的重點(diǎn)是相似三角形性質(zhì)定理的應(yīng)用，即在學(xué)習(xí)新知后，需要通過例題與習(xí)題的設(shè)計(jì)配合，讓學(xué)生明確三個(gè)應(yīng)用技能：一是了解相似指兩個(gè)圖形間的數(shù)量關(guān)系，與其所在位置無關(guān);二是明確相似三角形的對(duì)應(yīng)高、對(duì)應(yīng)角平分線、對(duì)應(yīng)中線之比都可以相互得到，并且它們有一個(gè)重要的橋梁聯(lián)系是相似比，任意一組對(duì)應(yīng)邊之比都可以得到相似比;三是學(xué)生需要從基本文字語言熟悉性質(zhì)，再學(xué)會(huì)由幾何直觀找到圖形中線段的關(guān)系，應(yīng)用性質(zhì)解題并滲透到實(shí)際問題中，抽象出數(shù)學(xué)模型，打開應(yīng)用的鎖.

一、利用習(xí)題，為學(xué)生由文字語言向幾何直觀認(rèn)知過渡搭建“小階梯”

針對(duì)本節(jié)課學(xué)習(xí)重點(diǎn)，在講解了相似三角形性質(zhì)定理后，筆者首先借助教材第107頁隨堂練習(xí)的檢測(cè)標(biāo)準(zhǔn)，進(jìn)行變式，讓學(xué)生體會(huì)完全的文字表述，目的在于使其熟悉相似三角形性質(zhì)定理的基本內(nèi)容與4個(gè)幾何量之間數(shù)量關(guān)系的相互轉(zhuǎn)換，為學(xué)生認(rèn)識(shí)新知搭建“小階梯”.

第一階段全文字表述習(xí)題訓(xùn)練：

以上五題，沒有任何計(jì)算難度，學(xué)生可以很快得到答案，并且通過反復(fù)的知識(shí)點(diǎn)串聯(lián)，進(jìn)一步強(qiáng)化對(duì)相似三角形性質(zhì)定理基本知識(shí)點(diǎn)的理解和掌握.在基礎(chǔ)落實(shí)后，筆者再讓學(xué)生做教材中第107頁隨堂練習(xí)兩個(gè)題目及第108頁習(xí)題4.11知識(shí)技能第1題.這三道題的難度與應(yīng)用程度相對(duì)之前的5個(gè)題大一些，學(xué)生的認(rèn)知“小階梯”便搭建完成.否則，按照教材中的設(shè)計(jì)，直接進(jìn)入符號(hào)語言線段成比例表示部分，學(xué)生是根本沒有辦法轉(zhuǎn)化為相似比認(rèn)知的.這樣有坡度的設(shè)計(jì)，可使學(xué)生輕松愉快地掌握知識(shí).

第二階段難度提升習(xí)題訓(xùn)練：

2.兩個(gè)相似三角形一組對(duì)應(yīng)角平分線的長(zhǎng)分別是2 cm和5 cm，則這兩個(gè)三角形的相似比是? ?;在這兩個(gè)三角形的一組對(duì)應(yīng)中線中，若較短的中線是3 cm，則較長(zhǎng)的中線是? ?.（教材第108頁隨堂練習(xí)2）

3.△ABC∽△A′B′C′，AD和A′D′是它們的對(duì)應(yīng)角平分線，已知AD=8 cm，A′D′=3 cm，則△ABC與△A′B′C′對(duì)應(yīng)高的比是? ?.（教材第108頁習(xí)題4.11知識(shí)技能1）

二、分解例題，為學(xué)生幾何直觀應(yīng)用性質(zhì)定理搭建“小階梯”

本節(jié)課例題，教材第107頁：

例1存在以下三個(gè)方面的難點(diǎn)：

1.本節(jié)課學(xué)生接觸的第一個(gè)幾何圖形過于復(fù)雜，會(huì)使他們產(chǎn)生畏難情緒，不利于后續(xù)教學(xué)的開展.

2.學(xué)生需進(jìn)行小三角形高的證明、相似的證明才能應(yīng)用到本節(jié)課重點(diǎn)知識(shí)，前面知識(shí)點(diǎn)障礙設(shè)置太冗長(zhǎng).

3.學(xué)生對(duì)于所求線段的認(rèn)知，無法直觀轉(zhuǎn)化為對(duì)應(yīng)線段之比.

針對(duì)以上學(xué)情難點(diǎn)，筆者對(duì)例題進(jìn)行了分解，首先由學(xué)習(xí)目標(biāo)指導(dǎo)——重視實(shí)際應(yīng)用，把題目投射到學(xué)校建筑選修課中，然后拆分例題圖形，使其轉(zhuǎn)化為兩個(gè)相似的三角形.

變式1：學(xué)校趣味建筑選修課學(xué)習(xí)建構(gòu)相似模型，現(xiàn)有△ABC∽△HSR，已知AB=4 dm，HS=2 dm，△HSR底邊SR上的高HE=1.5 dm，求△ABC對(duì)應(yīng)高AD的長(zhǎng)度.

教學(xué)目的：1.圖形簡(jiǎn)單，學(xué)生容易直接應(yīng)用相似三角形性質(zhì)定理。2.為教材例題做好兩個(gè)三角形相似的知識(shí)準(zhǔn)備.3.將以上兩個(gè)圖形進(jìn)行平移后就是原例題，再次強(qiáng)調(diào)相似是圖形間的數(shù)量關(guān)系，與其位置無關(guān)，為后面介入平移、旋轉(zhuǎn)、翻折的圖形變換作鋪墊.

變式2：如圖3所示，△ABC∽△ASR，AE是△ASR的高，AD是△ABC的高.

分解例題搭建“小階梯”后，學(xué)生便可以更清晰地認(rèn)識(shí)這個(gè)相對(duì)有些復(fù)雜的圖形.教師再滲透從特殊到一般的思想，學(xué)生便會(huì)借助直觀模型，建立數(shù)感.

三、變式例題，結(jié)合習(xí)題，為學(xué)生實(shí)際應(yīng)用性質(zhì)定理搭建“小階梯”

例題拆分講解時(shí)，我們始終貫穿一個(gè)思想認(rèn)識(shí)——相似是圖形間的數(shù)量關(guān)系，與其所在位置無關(guān).在例題中只體現(xiàn)了平移的圖形運(yùn)用，故筆者結(jié)合教材第108頁習(xí)題4.11問題解決2，通過變式3為學(xué)生實(shí)際應(yīng)用性質(zhì)定理搭建“小階梯”.

變式3：如圖4，在例1基礎(chǔ)上△ASR繞點(diǎn)A順時(shí)針旋轉(zhuǎn)180°.

若再將此圖整體旋轉(zhuǎn)180°，便得到了習(xí)題的抽象解題模型（如實(shí)際應(yīng)用）.為學(xué)生搭建了從實(shí)際問題中抽象數(shù)學(xué)模型從而解題的“小階梯”.

實(shí)際應(yīng)用（教材第108頁習(xí)題4.11問題解決2）：如圖5，小強(qiáng)自制了一個(gè)小孔成像裝置，其中紙筒的長(zhǎng)度為15 cm.他準(zhǔn)備了一支長(zhǎng)為20 cm的蠟燭，想要得到高度為5 cm的像，蠟燭應(yīng)放在距離紙筒多遠(yuǎn)的地方？

四、通過例題變式，滲透經(jīng)典模型，為激發(fā)學(xué)生探索興趣搭建“小階梯”

由例題的變式與習(xí)題實(shí)際應(yīng)用，學(xué)生會(huì)明確地感知相似是圖形間的數(shù)量關(guān)系，與其所在位置無關(guān)，并且可以很好地辨識(shí)圖形中的對(duì)應(yīng)線段，進(jìn)行相似三角形性質(zhì)定理的應(yīng)用.故在這里，筆者為學(xué)生展示了相似三角形性質(zhì)的應(yīng)用的經(jīng)典題型，作為學(xué)生的課后挑戰(zhàn)，激發(fā)學(xué)生的探索興趣.

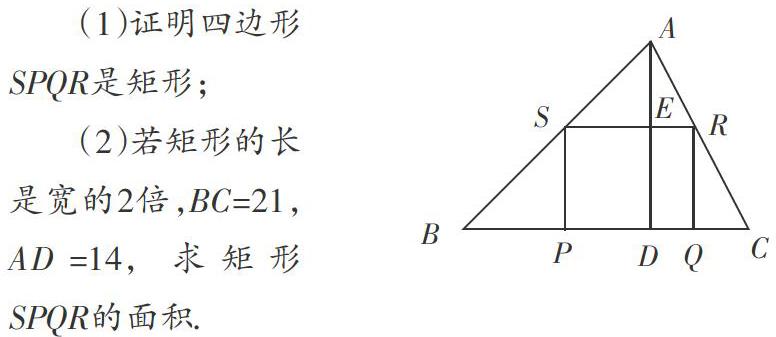
課外提升：在課堂例1的基礎(chǔ)上，我們對(duì)原圖形再次進(jìn)行變式探究，過點(diǎn)S作SP⊥BC于點(diǎn)P，過點(diǎn)R作RQ⊥BC于點(diǎn)Q.

（1）證明四邊形SPQR是矩形;

（2）若矩形的長(zhǎng)是寬的2倍，BC=21，AD=14，求矩形SPQR的面積.

教材是學(xué)之本，也是教之本，我們應(yīng)立足教材，針對(duì)不同學(xué)情，設(shè)計(jì)讓學(xué)生愛學(xué)、樂思的教學(xué)環(huán)節(jié)，借助例、習(xí)題的鋪墊、拆解、變式、結(jié)合，幫助學(xué)生搭建屬于自己的快樂學(xué)習(xí)數(shù)學(xué)的“小階梯”，讓以學(xué)生為主體的課堂更加生機(jī)勃勃！

責(zé)任編輯 邱 艷