基于分災模式鋼筋混凝土梁的承載力計算

陳劍波 （南京交通職業技術學院，江蘇 南京 211188）

0 引言

地震是一種很難預測的自然災害，給人類帶來了極大的生命和財產損失，如何對建筑結構進行合理的抗震設計一直是研究學者的關注熱點。與傳統的建筑抗震設計相比，引入分災模式理念的結構抗震設計，結構中的鋼筋混凝土梁抗彎加固性能必然會有所增加。梁正截面抗彎承載力的計算需考慮在原有的梁結構體系中所加入分災元件，分災元件為原結構的防災減災提供了第一道防線，第一道防線通過自身具有的耗能能力，更好地為原結構提供安全保障。

1 傳統結構設計中梁的受彎構件正截面承載力

1.1 基本假定

1.1.1 受彎構件截面平均應變的平截面假定

大量的實驗數據表現，對于受彎構件，特別是梁受彎構件，在進行受彎梁加載試驗的時候，梁構件在開始的荷載施加直到構件發生破壞的所有階段，受彎梁的截面所發生的應變基本都很好地符合了平截面假定，而對于受彎梁的受拉區，截面開裂后一分為二，不符合平截面的假定條件，但所引起的誤差并不大，同樣也可以認為與平截面假定相符合。通過采用平截面假定，才能進行受彎梁承載力計算公式的推導計算。

1.1.2 忽略受彎梁受拉部位混凝土的抗拉強度

在構件受力后，受彎構件的受拉區出現混凝土開裂時，意味著大部分裂開的混凝土其實已經不能承受荷載了，僅有一小部分仍承擔小部分拉力；因此，在這里可忽略不計受拉開裂混凝土的強度，這樣更方便計算。計算的結構會存在一定的計算誤差，但是誤差在允許范圍內，可忽略不計。

1.1.3 受壓區部位混凝土的應力應變關系

對于混凝土的受壓本構關系，采用簡化模型可得：

1.1.4 鋼筋的應力應變關系

采用理想的彈塑性應力—應變曲線：

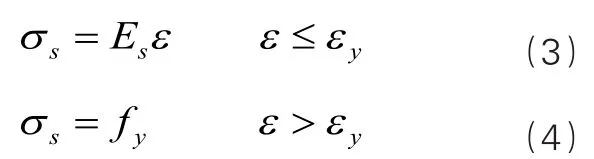
對于傳統的受彎梁正截面承載能力公式的推導與計算，需要考慮以上四個方面的假定和對應關系。

1.2 梁的受彎構件正截面承載力

通過混凝土受彎梁正截面承載能力的計算方法以及根據所采用相應的基本原則，引入建筑材料的安全系數，能夠推算出單筋矩形受彎梁的截面受彎構件承載能力計算公式，如下式所示：

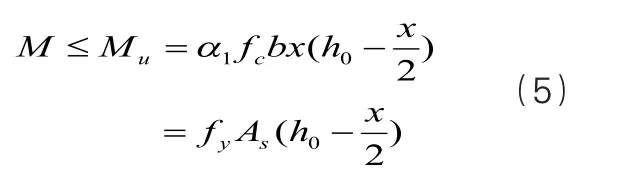
傳統的結構中，因為沒有采用分災設計理念，因此未曾引入分災元件。當建筑面臨地震荷載的時候，主要靠構件本身的承載力消耗能量，當地震荷載較大時，原有結構就會受到不同程度的破損甚至出現整體結構的破壞。這些破壞，在某種程度上是不可逆的。因此，只有引入了分災元件，才能實現多道分災防線，即使面臨較大地震荷載時，也是分災元件首當其沖；此時，在很多情況下，通過巧妙的設計，往往可以通過維修分災元件就能降低地震所帶來的各種破損，實現了較好的經濟效益。

2 分災模式的鋼筋混凝土梁抗彎加固性能評估

當考慮采用分災模式的設計理念，即在原有的建筑結構中加入分災元件，可以有效提高原有結構的抗震性能，加入的分災元件通過自身的能量消耗，成為抵抗地震的第一道防線，這樣一來，既不會破壞原有結構的主要功能，又有效地發揮了分災作用。加入分災構件后，因為分災構件的分擔作用，不能再單純地采用原有的鋼筋混凝土梁承載力的計算公式，必須要考慮新增構件的作用，考慮分災元件的影響因素，通過實驗數據以及理論推導，在計算公式中，增加新的分項系數來計算出分災模式下梁的承載力計算公式。

2.1 分災模式的鋼筋混凝土梁承載力計算

2.1.1 計算受彎梁的底初始拉應變

在國內的有關實驗數據可得出即使在分災模式設計下，梁受彎截面仍符合平截面設定。在計算分災模式受彎梁的初始拉應變時，可按照規范采用線性分布考慮，求得梁底正截面極限抗彎承載力與鋼筋應力應變關系。

采用單一材料時，考慮到通過用換算截面來代替梁未開裂時的鋼筋混凝土截面計算，可求出截面受壓區高度公式，如下式所示：

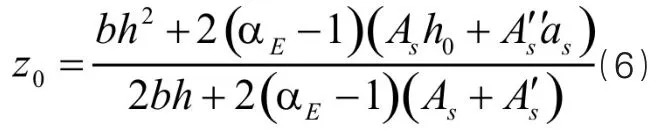
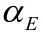
截面慣性矩公式如下：

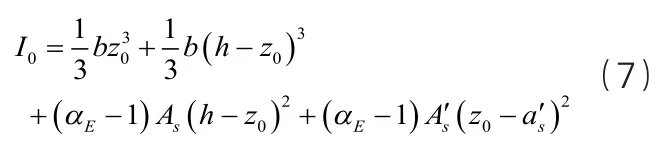
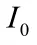
根據上述公式可計算出鋼筋混凝土梁抗彎加固梁底初始拉應變，公式如下：

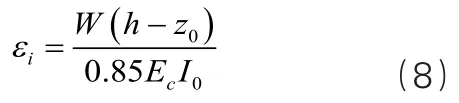
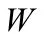
2.2 計算分災模式梁的正截面極限抗彎承載力

分災模式的鋼筋混凝土梁中混凝土合力計算公式如下：

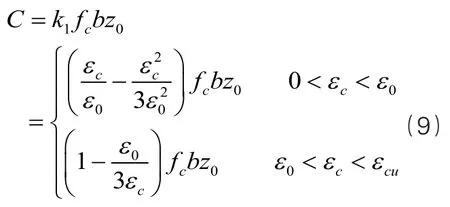
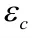
依據《混凝土結構規范》計算原則，可得出不同受壓區混凝土壓應變地與γ。當鋼筋混凝土受彎梁在進行抗彎加固后，在水平向達到平衡時，梁正截面的極限抗彎承載力為：

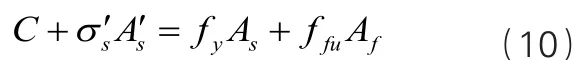
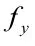
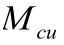
3 結語

通過比較不考慮分災元件以及考慮分災元件的受彎梁承載能力公式，可知分災元件有效地提供了抗震防線，提高了原有結構的可靠度。利用該方法對原建筑結構進行加固，不僅施工簡便、經濟效益強，且進行抗彎加固后仍可維持原有建筑的大部分使用功能。考慮分災模式的設計方法，將是以后建筑結構設計的發展方向，設計師通過合理的設計，科學地設計分災元件的截面性質、元件的分布位置、元件與原有結構的連接方式，最終有效地成為了原有結構的第一道有力的抗震防線。