雙定子高溫超導電機阻尼繞組對超導勵磁磁場及電樞反應磁場作用機理分析*

王 睿， 王玉彬， 朱新凱

[1.中國石油大學(華東)新能源學院，山東 青島 266580；

2.東南大學 電氣工程學院， 江蘇 南京 210096]

0 引 言

近年來，隨著直驅風力發電技術的快速發展，對發電機的功率密度以及容量等級要求越來越高。傳統直驅發電機因其體積和重量過大，限制了風力發電技術的進一步發展。與傳統直驅發電機相比，超導直驅發電機則因具有體積和重量小、結構緊湊、功率密度和效率高、穩定性好等優點[1-2]，受到廣泛關注。與低溫超導電機(LTSM)相比，高溫超導電機(HTSM)的制冷系統技術難度及所需制冷量大大降低，得到了快速發展[3-4]。得益于超導線材的高通流能力，HTSM的勵磁繞組部分采用超導勵磁繞組[5]取代常規永磁體或銅質勵磁繞組，較少匝數的超導勵磁線圈即可產生強氣隙磁場，使大容量HTSM體積和質量大大減小。因此，HTSM在直驅風力發電、船舶電力推進以及航天發射等領域具有潛在的應用前景。

超導線材維持超導性必須同時滿足臨界電流Jc、臨界溫度Tc以及臨界磁場Hc[6]3個臨界條件。當超導線材放置在低溫冷卻介質中，如(77 K)的液氮環境下，可以滿足其對臨界溫度的要求。但當超導(SC)線圈位于磁場環境復雜的電機系統中時，磁力線一旦沿鐵心進入勵磁磁場環境,很容易影響超導勵磁線圈的超導特性，導致其脫離超導狀態[7]。因此，研究HTSM中SC線圈周圍的磁場變化對超導線材臨界電流的影響，對預防超導勵磁線圈失超具有一定借鑒價值。

為減弱磁場對SC線圈的影響，降低超導勵磁線圈的失超風險，超導電機內部一般會采用電磁屏蔽層。文獻[8]結合HTSM的特性，針對單一屏筒式阻尼屏蔽系統的弊端，提出了多屏筒式阻尼屏蔽系統。文獻[9]則利用鼠籠式阻尼導條的渦流特性，針對DS-HTSM，提出鼠籠式阻尼導條與銅屏蔽層相結合的方法。雖然這種組合式電磁屏蔽方案有效地減弱了交變磁場可能引起的SC線圈失超風險，但是其具體的作用機理并未進行深入的理論分析，值得進一步研究。

鑒于此，本文建立了DS-HTSM的靜止氣隙磁導模型，通過解析方法分析阻尼繞組對SC線圈交變磁場的影響，并應用有限元驗證所提分析方法的正確性。

1 DS-HTSM結構及工作原理

圖1為DS-HTSM結構的平面示意圖。為便于實現勵磁繞組的靜態密封[9]，DS-HTSM采用雙定子結構配置。其中，勵磁繞組放置在內定子的冷卻杜瓦中，電樞繞組放置在外定子上，轉子則由調磁塊和非調磁塊間隔排列組成。同時，類似于內定子極靴的導磁環還可為電樞磁反應場提供切向磁路，從而降低電樞反應磁場對超導勵磁繞組臨界電流的影響。

圖1 DS-HTSM結構圖

參考文獻[10]，DS-HTSM基于氣隙磁場調制工作原理實現機電能量轉換。勵磁磁場經調磁環轉子調制出的有效諧波磁場極對數與電樞反應磁場極對數相對應，且內定子極對數Pin、外定子極對數Pout和轉子極數Nr之間滿足式(1)：

Pout=|Pin-Nr|

(1)

同時，電樞諧波磁場的轉速Ωa與轉子轉速Ωr之間滿足式(2)：

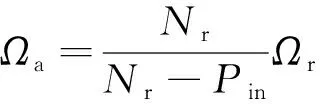
(2)

在合理的內外定子極對數配合下，DS-HTSM可以實現低速直驅功能。

2 內氣隙磁場解析

對于超導勵磁繞組置于內定子側的DS-HTSM而言，內氣隙磁場和SC線圈直接作用，因此本文主要針對內氣隙的磁通密度進行分析。圖2所示是帶有鼠籠式阻尼繞組的DS-HTSM結構。

圖2 帶有阻尼導條的DS-HTSM結構配置

通常，負載運行工況下，DS-HTSM氣隙中同時存在勵磁磁場和電樞反應磁場，因此在研究鼠籠式阻尼導條對SC線圈周圍諧波的影響時，要分別對這2種磁場加以考慮。為了方便定性分析阻尼繞組的作用，對電機結構模型作出如下假設：

(1) 內外定子鐵心和調磁塊的磁導無限大，忽略磁飽和影響；

(2) 忽略端部效應及磁極疊片中渦流效應的影響；

(3) 由于阻尼導條的半徑較小，且放置在閉口槽中，暫不考慮阻尼導體漏阻抗的影響；

(4) 阻尼導條中電流沿軸向均勻分布。

2.1 磁導解析式

基于磁場調制原理，根據雙定子類電機的勵磁磁動勢、電樞磁動勢、調磁環轉子磁導、外定子磁導及內定子磁導分布，同時借助傅里葉分解，可以分別得到勵磁磁場和電樞反應磁場經調制后產生的內氣隙磁通密度分布[11]。

圖3所示為調磁環轉子磁導波形。

圖3 調磁環轉子磁導波形

可得調磁環轉子磁導λr(θ,t)(不計非調磁塊通過的少量磁通)如下：

(3)

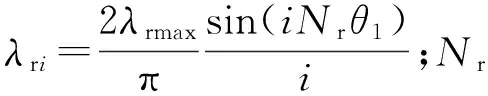
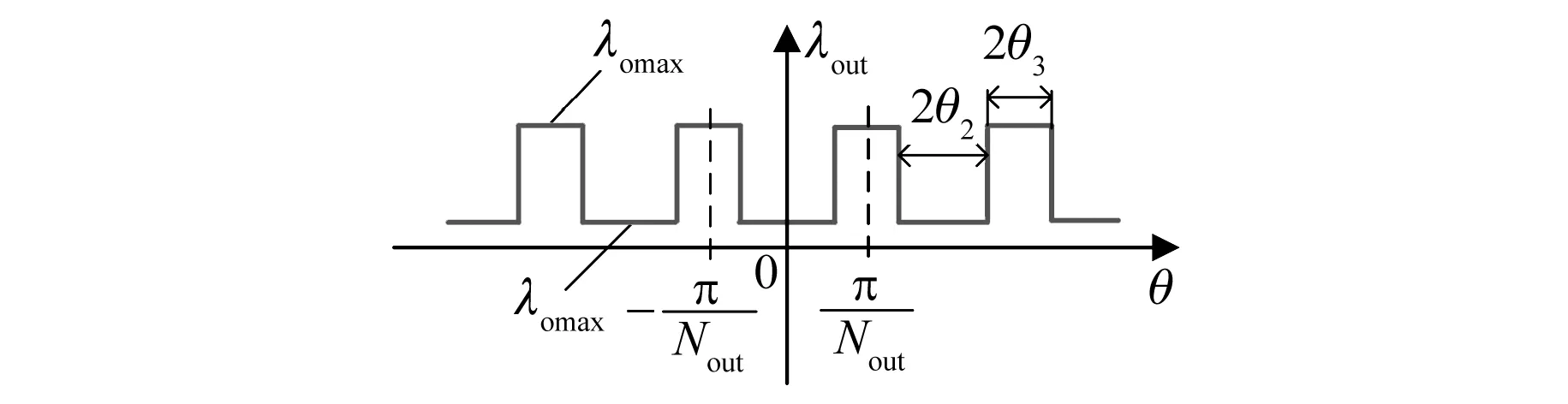
圖4 外定子磁導波形

磁導λout(θ)表達式為

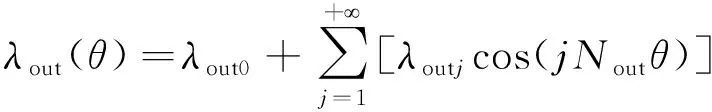
(4)

圖5所示為DS-HTSM電機內定子磁導λin(θ)的分布波形。

圖5 內定子磁導波形

λin(θ)表達式為

(5)

2.2 勵磁磁場產生的內氣隙磁密

勵磁磁場產生的內氣隙磁密是指當電機空載運行時，僅勵磁磁場作用，勵磁磁動勢經調磁環轉子以及內定子齒共同調制，在內氣隙中調制產生的氣隙磁密。圖6所示為勵磁磁動勢波形(計及內定子齒的作用)。

根據圖6可以得到空載時DS-HTSM的勵磁磁動勢ff(θ)：

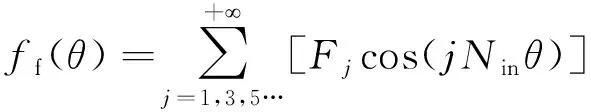
(6)

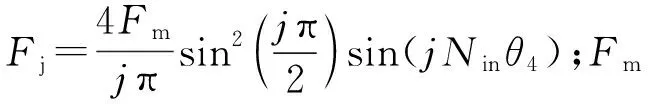
圖6 勵磁磁動勢波形

圖7所示的勵磁磁場磁路，主要包括穿過內外氣隙的閉合磁路及直接經導磁環閉合的回路兩部分，其中，前者是重點研究內容。

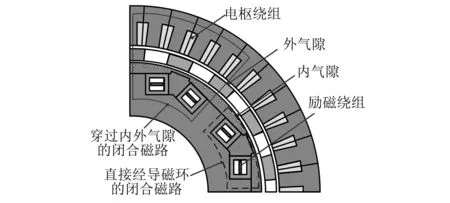
圖7 勵磁磁場磁路圖

結合式(3)和式(6)可以得到勵磁磁動勢經由調磁環轉子調制而產生的內氣隙磁密Binf(θ,t)：

Binf(θ,t)=ff(θ)·λr(θ,t)=

(7)

2.3 電樞反應磁場產生的內氣隙磁密

文獻[11]中給出了三相電樞繞組的合成磁勢fa(θ,t)(計及外定子齒槽影響)：

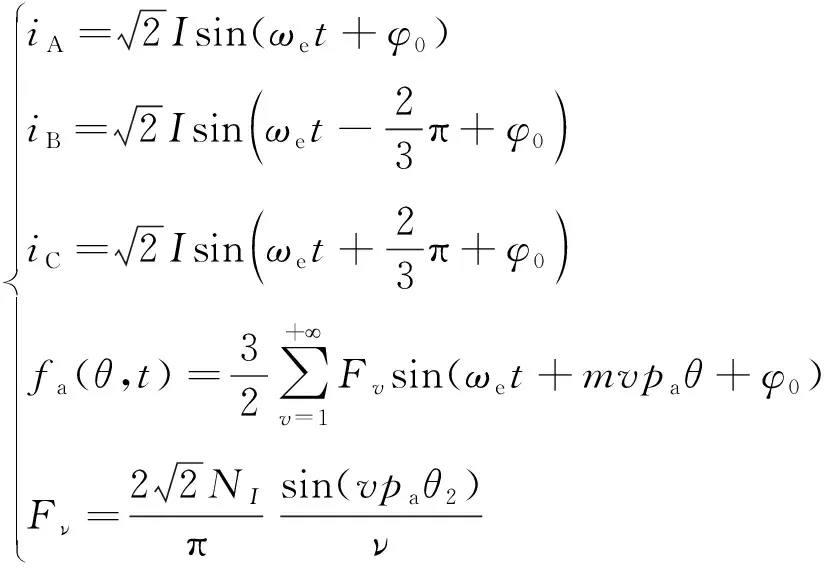
(8)

圖8所示為電樞反應磁場磁路，虛線表示不經過阻尼導繞組的磁力線路徑，實線為對阻尼繞組產生作用的電樞反應磁場路徑，其中前者為主導。

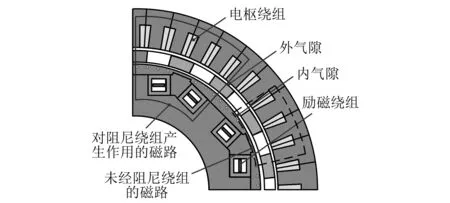
圖8 電樞磁場磁路圖

電樞反應磁場經調磁環轉子以及內外定子齒共同調制產生的內氣隙磁密Bina(θ,t)如下：

Bina(θ,t)=f2(θ,t)·λr(θ,t)·λin(θ)=

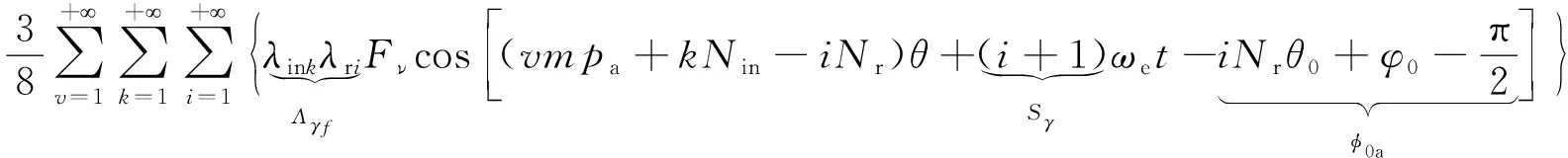
(9)

3 阻尼繞組中的感應磁場解析

為了方便后續分析，需對電樞反應磁場和勵磁磁場分別單獨作用下產生的內氣隙磁密進行簡化。將氣隙磁通密度統一表達為

Bin(θ,t)=Fγ(θ,t)Λγ(θ,t)

(10)

則式(7)和式(9)可進一步簡化表達為

(11)

式中:Λγ為內氣隙總磁導，Fγ為諧波磁勢幅值，根據磁動勢調制來源分為Fγa和Fγf；γa和γf為內氣隙諧波磁場極對數；sγ為內氣隙諧波磁場相對電樞磁場旋轉速度的倍數；φ0為γ次諧波磁場；Λγa為電樞磁場單獨作用時的內氣隙磁導，等于內定子磁導與轉子磁導的乘積，如γa取|νmpa|時，對應Λγa為 (λr0·λin0)，同理，定義Λγf為勵磁磁場單獨作用時的內氣隙磁導，即λri。

設DS-HTSM內定子一個極距內共有2nc根阻尼導條，當內氣隙磁場與阻尼條有相對運動時，則會在端部閉合的阻尼條中產生感應電流，繼而電磁感應生成交流磁場，作用于原交變磁場。

3.1 阻尼導條中的感應電流

由于不同阻尼回路所占空間面積對應的相位差不同[12-13]，將其分為極弧回路(沿d軸對稱)和極間回路(沿q軸對稱)。其中，內定子的外徑用Rin表示，內定子的極對數用pin表示。以勵磁磁場作用于阻尼繞組為例，從極弧與極間回路分別說明不同類型阻尼回路中感應電流原理。

3.1.1 勵磁磁場γ次諧波磁勢在極弧(沿d軸對稱)回路的感應電流

首先，選擇同一定子齒對應的一個極距內相鄰2根阻尼導條作為一個阻尼回路，阻尼導條之間的弧長為l1。根據弧長公式計算對應的空間機械角度，為α1=l1/Rin，得到電樞磁場γ次諧波在極弧阻尼回路中的感應電動勢為

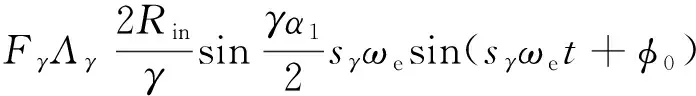
(12)

忽略端部阻抗及槽漏抗，則極弧下對應的阻尼回路等效電路如圖9所示。

圖9 極弧阻尼回路等效電路

其中，每根阻尼導條的電抗相同:

x1=x2=x3=…=x

(13)

對應極弧下的阻尼回路中的電流幅值相同:

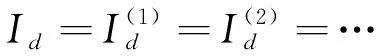
(14)

根據圖9中等效電路的虛線標記回路，列寫的電動勢平衡方程式為

(15)

式中：x為極弧阻尼回路的氣隙電抗,x=sγωeλγ1;λγ1為勵磁磁場經過單位軸向阻尼導條的氣隙磁導,λγ1=μ0l1/δe;δe為等效內氣隙長度。

結合式(12)～式(15)可得單個極弧回路中阻尼導條中的電流為

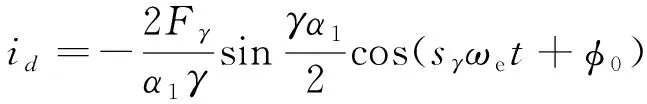
(16)

3.1.2 勵磁磁場γ次諧波在極間(沿q軸對稱)回路的感應電流

選擇不同定子齒對應的一個極距內相鄰2根阻尼導條作為一個阻尼回路，極間兩根阻尼導條之間的弧長為l2，按照弧長公式，對應的空間機械角度為α2=l2/Rin，確定勵磁磁場γ次諧波在極間阻尼回路中的感應電動勢為

(17)

同理，不計端部阻抗和漏抗，則極間阻尼回路等效電路如圖10所示。

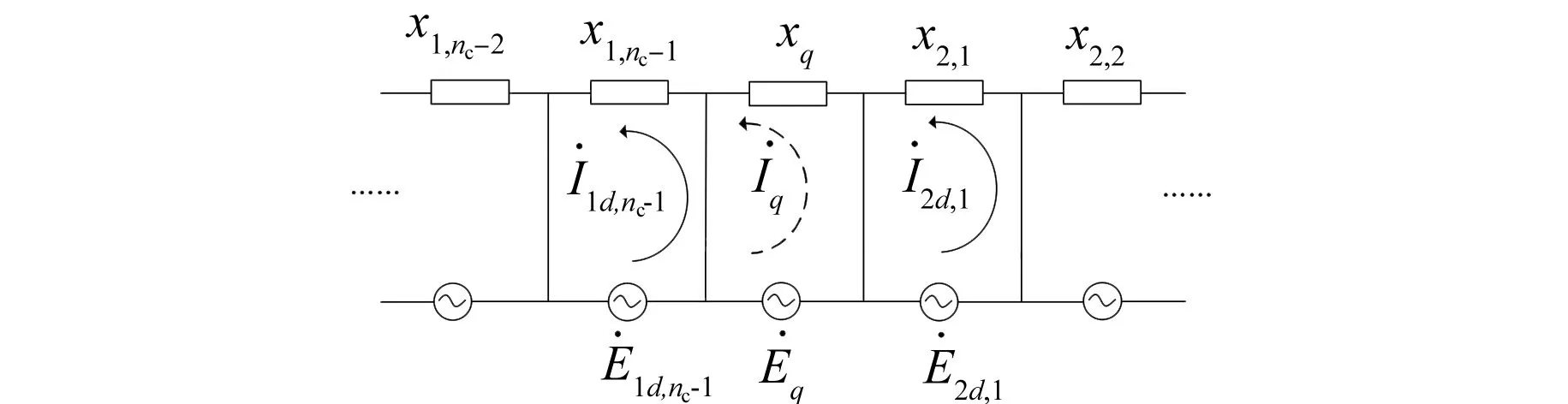
圖10 極間阻尼回路等效電路

對比極弧阻尼回路電流方程，根據圖10中等效電路的虛線標記回路，極間回路的電動勢平衡方程列寫為

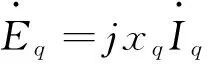
(18)

式中：xq為阻尼導條回路的氣隙電抗,xq=sγωeλγ2；λγ2為勵磁磁場經過單位軸向阻尼導條的磁導,λγ2=μ0l2/δe;δe為等效內氣隙長度。

同理，結合式(17)和式(18)可得單個極間回路中阻尼導條中的電流為

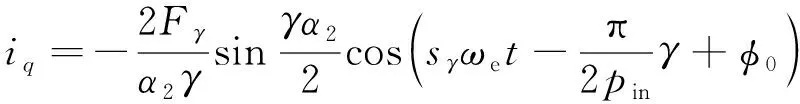
(19)

3.2 阻尼繞組中的感應磁動勢

根據電磁感應定律，阻尼回路中的電流生成磁場，反過來作用到勵磁磁場。DS-HTSM中的2nc×2pin根阻尼導條采用鼠籠導條式結構設計加工，為了方便計算，在推導極弧阻尼回路(沿d軸對稱)和極間阻尼回路(沿q軸對稱)的磁動勢[14]時，選擇圖11所示的連接條部分。

圖11 阻尼回路連接圖

3.2.1 極弧下阻尼回路產生的磁動勢

阻尼回路連接如圖11所示，取一個極面上靠近中線相鄰2根阻尼導條構成1-1′回路，同時取阻尼回路的中線為坐標軸。由于電機內定子每個磁極下對應1-1′回路，共2pin個1-1′回路。

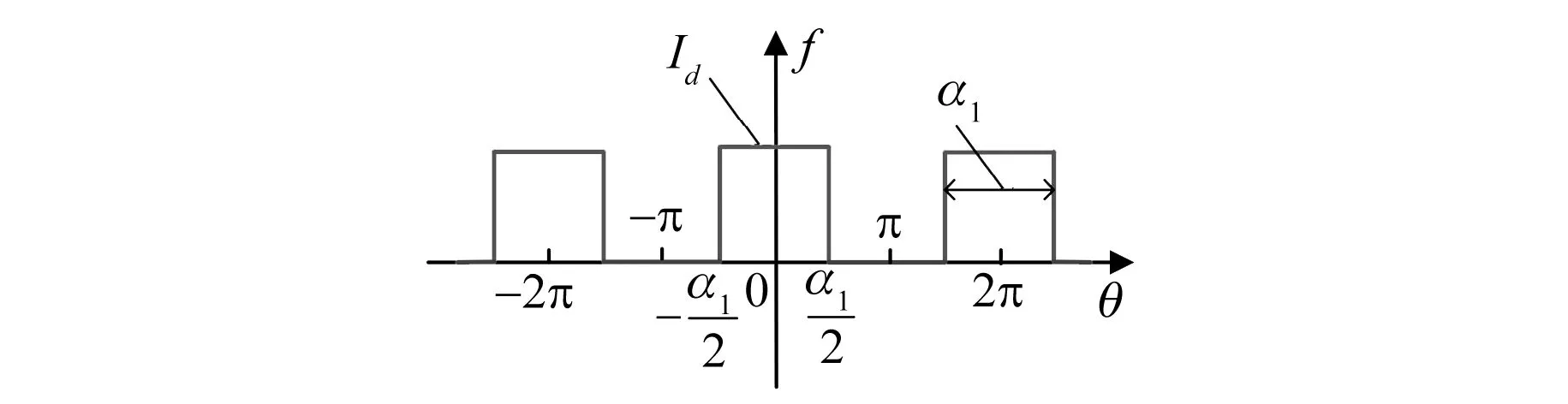
圖12 極弧下單個阻尼回路感應磁勢波形

圖12所示為一個磁極對應的1-1′回路磁動勢波形，進行傅氏分解可得

cos(sγωet+φ0)cos(μθ)=

cos(sγωet±μθ+φ0)

(20)

由圖11可知，沿順時針方向，相鄰磁極阻尼回路的電流滯后第1個磁極的 1-1′阻尼回路電流πγ/pin，在空間上相差π/pin，因此第2個磁極的1-1′阻尼回路電流的感應磁動勢為

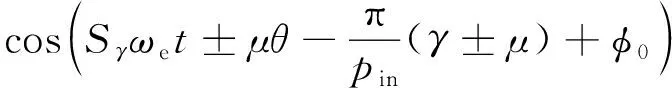
(21)

同理，第n個磁極下的1-1′阻尼回路電流的感應磁動勢為

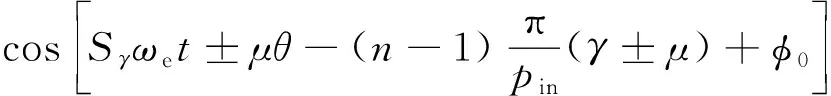
(22)

則電機中2pin個1-1′阻尼回路的總磁動勢為

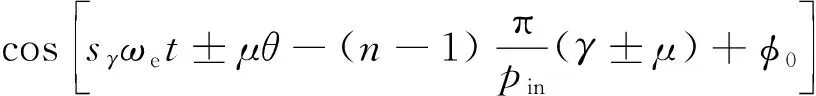
(23)

可見，阻尼回路電流在感應γ次諧波磁動勢之外，還會在內定子上產生其他的齒諧波感應磁動勢。此時，取μ=γ+2Kpin(其中,K=0,±1,±2,…,正負號代表齒諧波感應磁動勢相對γ次諧波旋轉方向)，則2Kpin次諧波磁動勢即為內定子開槽引起的齒諧波附加磁動勢。進一步簡化可以得到

cos[sγωet-μθ+φ0]

(24)

由圖11還可知，由于1′-2′回路電流滯后1-1′回路α1γ，在空間上相差α1，則2pin個磁極下1′-2′阻尼回路的總磁動勢為

cos[sγωet-μ(θ-α1)-α1γ+φ0]=

cos[sγωet-μθ-α1(γ-μ)+φ0]

(25)

由于阻尼回路以極面中心對稱，極弧下的阻尼回路幅值相等，按照繞組的分布規律，總磁動勢可以表達為

cos[sγωet-μθ-(m-1)α1(γ-μ)+φ0]=

(26)

3.2.2 極間阻尼回路產生的磁動勢

圖11中，1q回路代表一個極間阻尼回路。由于1q回路電流落后極弧下1-1′回路πγ/2pin，在空間上相差π/2pin，1q阻尼回路的磁動勢為

(27)

同理，對于其他極間阻尼回路感應的磁動勢可表示為

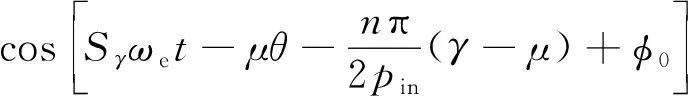
(28)

其中，n=1,2,3,…,Nd。

極間阻尼回路的總磁動勢為

(29)

3.2.3 所有阻尼回路產生的總磁動勢

阻尼回路的磁動勢滿足向量基本定理，則將極弧阻尼回路總磁動勢和極間阻尼回路總磁動勢，即式(26)和式(29)相加，可以得到所有阻尼回路的總磁動勢F可表示為

F=Fd+Fq=

cos[Sγωet-(γ+2Kpin)θ+φ0]=

cos[Sγωet-(γ+2Kpin)θ+φ0]

(30)

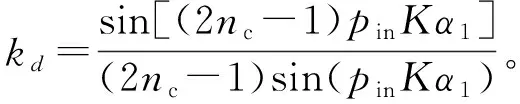
3.3 阻尼繞組感應磁動勢對氣隙磁場的影響

在考慮阻尼繞組產生的磁動勢對氣隙磁場的影響時，需保證在對電樞反應磁場發揮有效作用的同時，基本對勵磁磁場無影響。以圖2所示的DS-HTSM為例，結合表1中電機的部分參數，分析阻尼繞組對諧波磁場的影響。

表1 DS-HTSM部分參數

3.3.1 阻尼繞組磁動勢作用于電樞磁場

由式(30)分析可知，電樞反應磁場經由調磁環轉子和內定子齒共同調制產生的γa次齒諧波磁場切割阻尼繞組會感應出γa+2Kpin次諧波磁場，其中，2Kpin次諧波為附加齒諧波磁場。隨著諧波次數的增加，磁場諧波幅值減少，故僅分析K值取10以內。

當K=0，kd=7時，式(30)的幅值為負，故阻尼導條中感應出與主磁場反向的磁動勢，從而起到削弱γ次諧波磁場的作用，此時對于所有的高次諧波皆可以應用。從圖13可看出，當K取非零整數時，繞組分布系數kd的值呈周期性分布，且幅值在±0.71之間，同時，由于其在一個周期內有正有負，從而導致阻尼導條中感應出高次諧波磁動勢的方向無法確定。故只研究一個周期內的隨著K值變化，阻尼導條對高次電樞諧波磁場的影響。

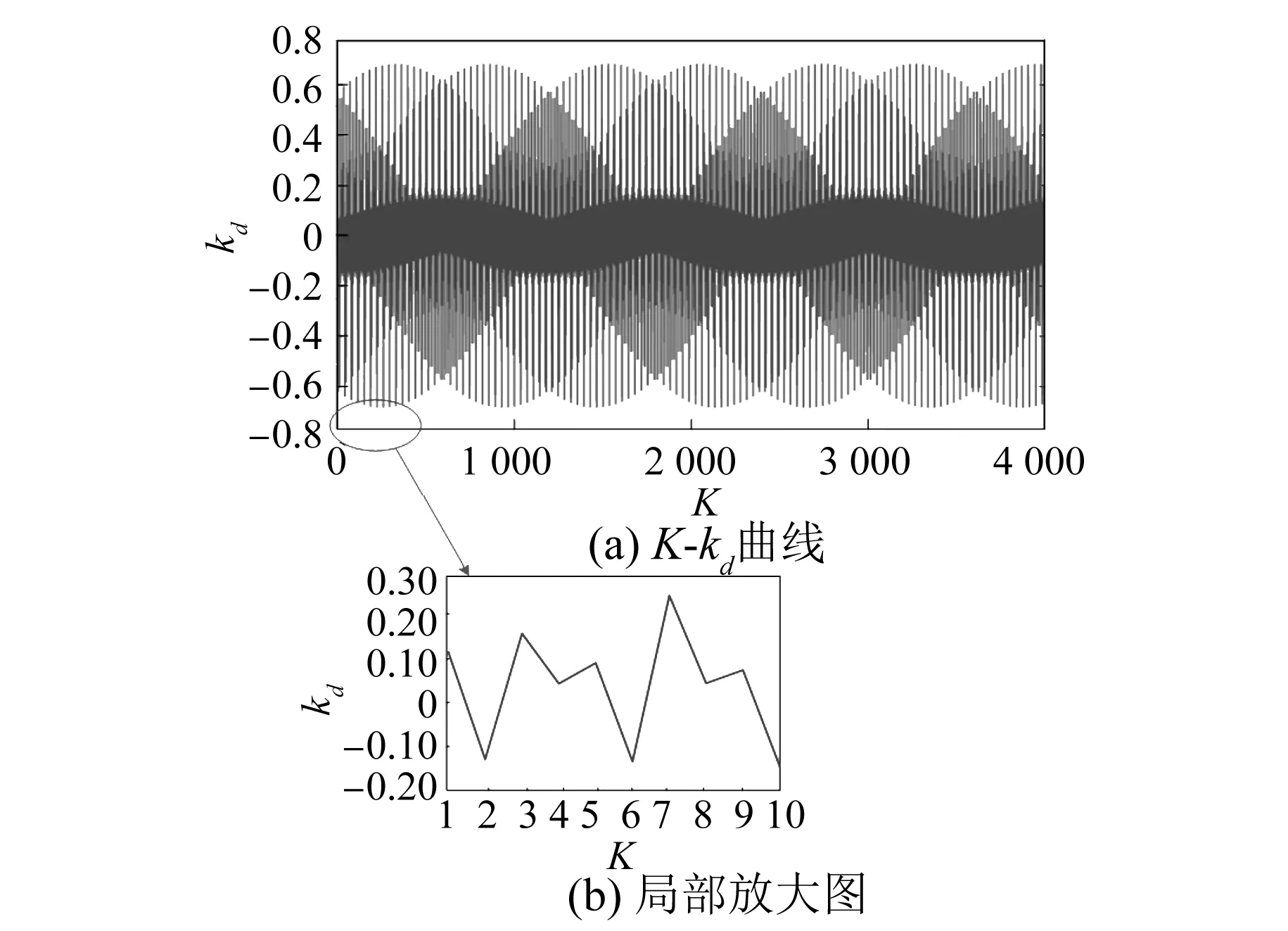
圖13 K-kd曲線圖

當K=±1，kd取正值時，式(30)中第1項取正值，第2項取負值，但是第1項的幅值遠大于第2項，且幅值和為負，因此阻尼導條中感應出的附加齒諧波磁動勢與主磁場反向，可以削弱有效電樞諧波磁場的磁動勢，即|vmpa+kNin|、|vmpa+kNin-iNr|。當K取偶數時，由于對應的kd正負值不一致，要分別分析：當K=±2, ±6, ±10，kd取負值時，式(30)中第1項取負值，第2項取正值，但是第1項小于第2項的幅值，幅值和為較小的正值，因此會小幅度地增強γa±4pin、γa±12pin、γa±20pin次電樞諧波磁場；當K= ±4,±8，kd取較小的正值時，第1、2項均取正，幅值和也為較小的負值， 因此對于γa±8pin、γa±16pin、γa±20pin次電樞諧波磁場而言，也是小幅度增強。同理可以分析K取奇數時，當K=±3，±5，±7，±9，kd取正值時，式(30)中幅值和的第1項取正值，第2項取負值，但是第一項的幅值大于第2項，幅值和取負值，因此可以削弱γa±6pin、γa±10pin、γa±14pin、γa±18pin次電樞諧波磁場，但是變化程度很小。總的來說，當K取大于±1的值時，阻尼導條對有效諧波之外地偶數次齒諧波磁場影響很小，而對|vmpa+kNin|、|vmpa+kNin-iNr|的有效諧波磁場可以進行抑制。

3.3.2 阻尼繞組磁動勢作用于勵磁磁場

同樣地，結合式(30)可以得到，勵磁磁場經調磁環轉子調制產的γf次交流諧波切割阻尼繞組會感應出γf+2Kpin次附加齒諧波磁場。下面研究一個周期內的K值變化時，阻尼導條對勵磁交流諧波磁場的影響。

當K=0時，kd=7，式(30)的幅值和為負，阻尼導條中感應出與主磁場反向的磁動勢，從而起到削弱γf次即|jNin±iNr|次諧波磁場的作用；而當K不為0時，阻尼導條中感應2Kpin次附加齒諧波磁勢，僅對偶次諧波有微弱影響，而對直流勵磁磁場無影響。

然而由于超導勵磁磁場遠強于阻尼繞組磁場，對超導勵磁場的影響可以忽略，后續的有限元分析也證明了這一點。綜上所述，DS-HTSM在放置阻尼繞組后，對勵磁直流磁場基本無影響，而對于交流電樞磁場的有效諧波起到削弱作用，即針對基波磁場發揮作用。

4 有限元驗證

借助有限元分析軟件進行分析時，忽略電機的端部效應，采用二維電磁場模型進行分析。且由于電機是整數槽繞組，滿足對稱性，為簡化模型運行，故采用二分之一模型進行分析。同時，在對比分析添加阻尼導條結構對勵磁特性的影響時，要保證模型設置的條件、參數以及網格剖分大小始終不變，僅改變阻尼導條的材料以及電路參數，通過對比是否添加阻尼導條時，DS-HTSM超導勵磁線圈的磁密變化，來驗證前述理論的正確性。

鑒于超導電機結構對稱，內定子四對極下對應圓周位置性能一致，因此只需分析一個SC線圈上的磁場。因鐵磁材料的磁阻遠小于杜瓦中空氣磁阻，大部分的徑向電樞磁力線沿內定子軛部(圖中實線部分)穿過，而少量的電樞磁力線沿內定子極靴圓周經阻尼導條穿過。因此，根據電樞反應磁力線的閉合路徑，結合阻尼導條的作用機理，僅研究沿切向的電樞磁力線對SC勵磁繞組的影響即可。在SC線圈表面沿切向均勻取6個磁密指示點(包含邊角位置)，分析SC線圈周圍的諧波磁場，如圖14所示。設置電路參數時，按照超導電機設計時取槽滿率為0.7，在電樞繞組上通入28.28 A的三相對稱電流，勵磁繞組通入40 A的直流電流。6個磁密指示點的切向磁密的頻譜分析結果如圖15所示。

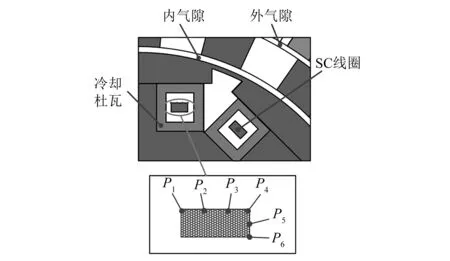
圖14 SC線圈的具體取點位置

SC線圈工作在超導狀態的條件之一是處于臨界磁場中，而電樞反應高次諧波磁力線進入內定子后，交變的磁場會直接影響SC線圈周圍恒定的臨界磁場，甚至會通過電磁感應在SC線圈上感應出附加電流，影響另一個條件—臨界電流。因此，必須要減少電樞反應高次諧波磁力線進入到勵磁磁場中。

由圖15的SC線圈磁密對比可以看到，在加入阻尼導條后，勵磁繞組對應位置的基波磁密分別被削弱了0.19、0.78、0.29、0.57、0.16、0.10 mT，即分別下降了23%、65%、45%、52.1%、48.48%、35.7%。但是對于其他極對數的諧波，無論是奇次還是偶次，相比于基波磁密的變化量而言，其值很小。圖15中的5次諧波，盡管基本上處于增強的狀態，但是從整體來看，其平均增加幅度以及幅值很小，可忽略不計。因此，阻尼導條中感應出的諧波磁場主要是用于減少90 Hz的基波電樞磁場對勵磁磁場的影響。同時，從圖16所示的空載內氣隙磁密曲線中可以看出，未加阻尼導條與加阻尼導條后的內氣隙磁密曲線是基本一致的，說明DS-HTSM在放置阻尼導條后，對勵磁磁場基本上無影響。

圖15 SC線圈上6個磁密指示點的諧波頻譜

圖16 空載時內氣隙磁密曲線圖

對比理論式推導和有限元仿真結果可以發現，DS-HTSM的電樞反應磁場經調磁環轉子和內定子調制產生的γa次交變諧波磁場作用于SC線圈，在極靴上放置鼠籠式阻尼導條結構后，利用阻尼回路的電磁感應效應，可以有針對性地降低幅值較高的基波電樞磁場對勵磁線圈的影響，而由阻尼導條感應的附加齒諧波磁動勢，對電樞繞組的高次諧波磁動勢則影響較小，同時對勵磁磁場也基本上無影響。這充分說明，阻尼導條結構在保證原勵磁磁場強度基本不變的前提下，可減弱基波電樞反應磁場對SC線圈的影響。

5 結 語

本文使用解析法詳細地分析了DS-HTSM中所應用的鼠籠式阻尼繞組對SC線圈周圍諧波磁場的影響，然后借助有限元法進行了對比驗證。電樞反應磁場經由內定子齒和調磁環轉子調制產生的內氣隙磁密，進入內定子后在阻尼導條中感應出電流，繼而由于電磁感應生成一系列的附加齒諧波，反作用于原磁場，尤其是針對基波交流電樞反應磁場，起到很強的削弱作用，對勵磁磁場的影響不大。