解析壁面函數的可壓縮效應修正研究
王新光,陳 琦,萬 釗,張愛婧,陳堅強
(1. 空氣動力學國家重點實驗室,綿陽 621010;2. 中國空氣動力研究與發展中心計算所,綿陽 621000)
0 引 言
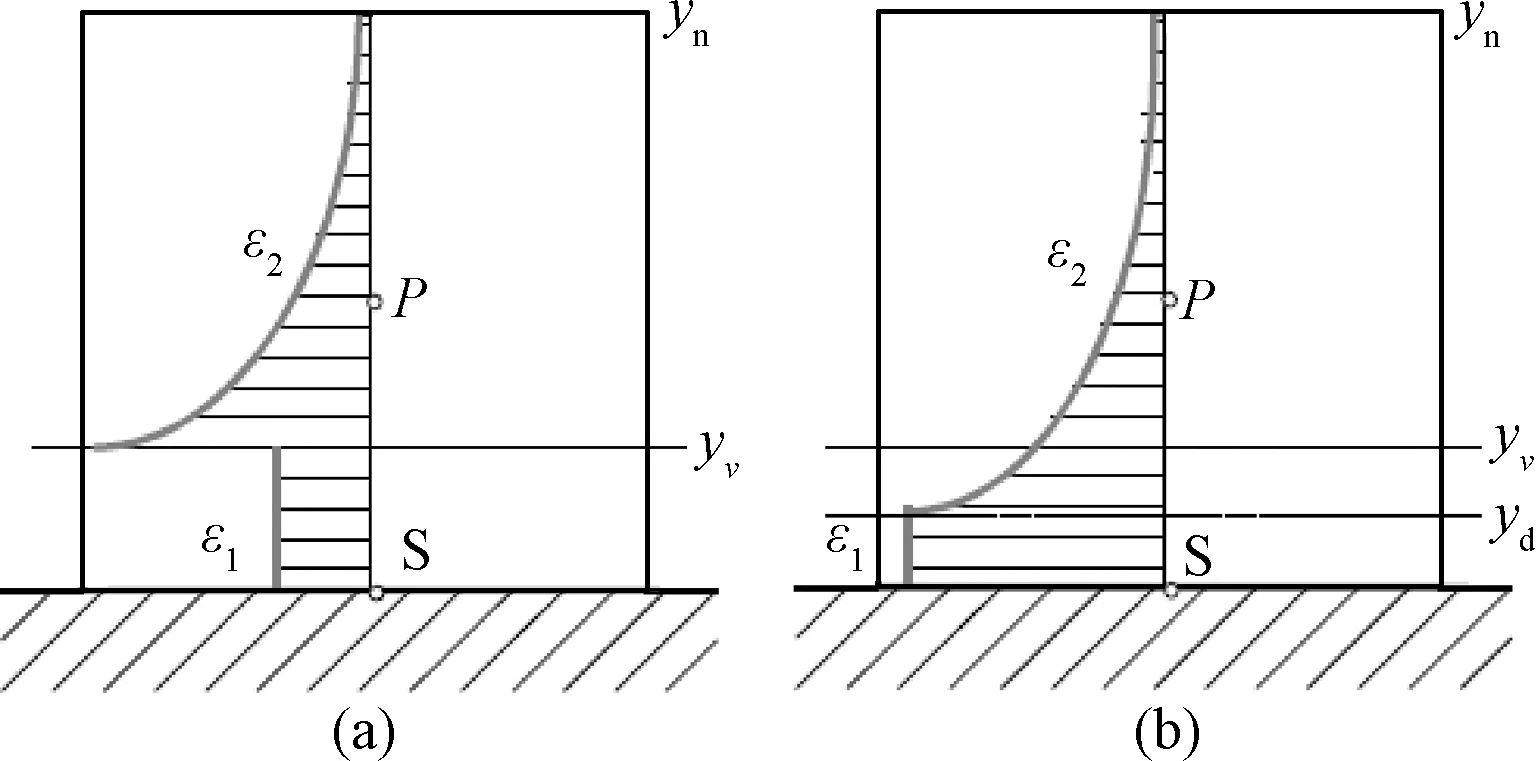
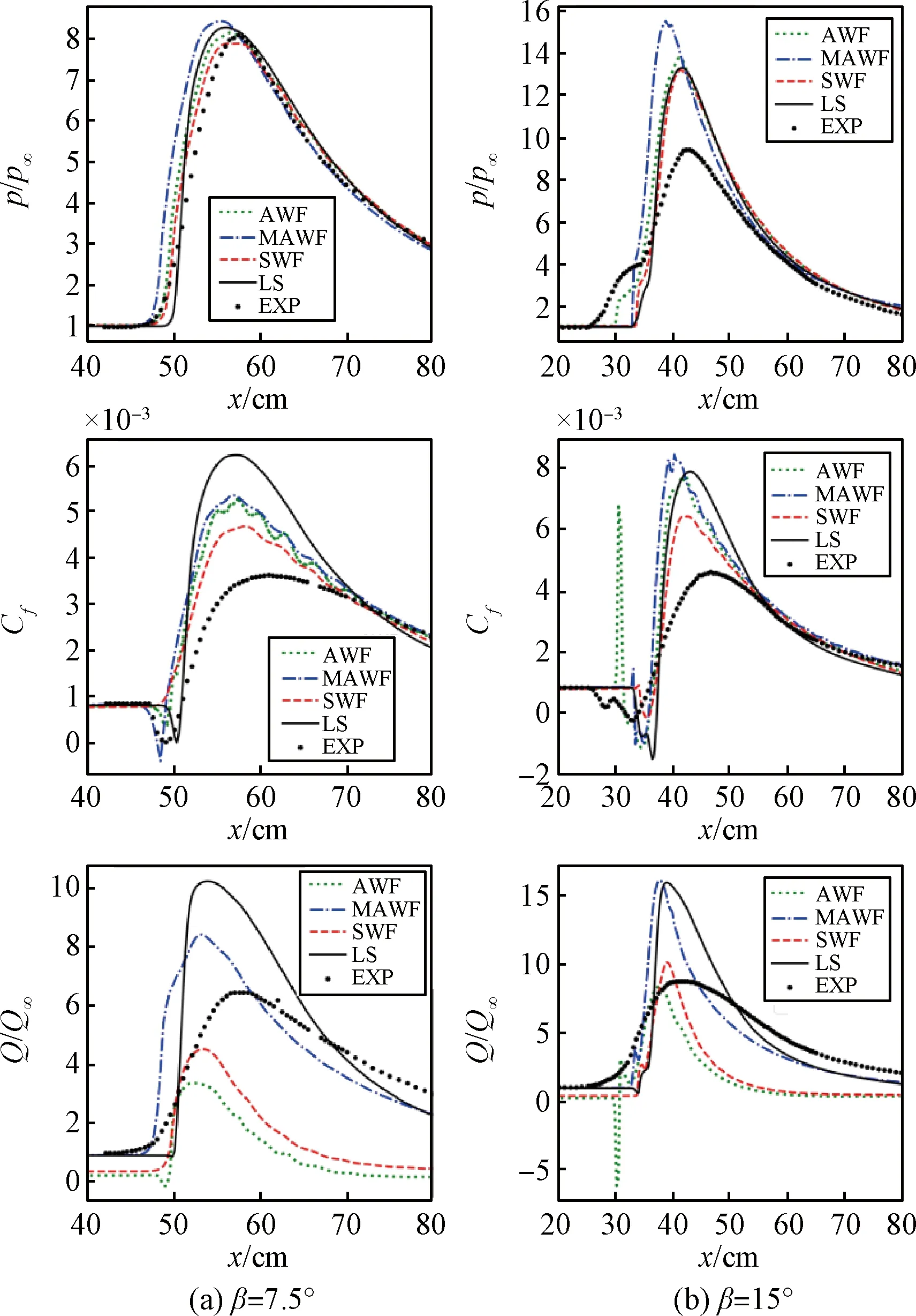
近年來,國家對于研發具有自主知識產權的自主品牌計算流體力學軟件,給予了前所未有的重視。眾所周知,湍流流動廣泛存在于航空、航天、航海以及人們的日常生活中,湍流模擬方法是計算流體力學界長期以來面臨的研究難題和研究熱點。商業軟件中通常使用RANS方法模擬湍流,常常需要在黏性底層中布置一定數目的網格點(通常y+≈1),從而使得壁面附近的網格十分細密,不僅會極大地增加迭代收斂的計算步數,還會帶來較為嚴重的數值剛性問題,從而導致迭代計算的穩定性下降。在復雜外形的數值計算中,網格量驟增,導致90%的計算時間都消耗在壁面附近1%計算域內。因此,目前主流商業軟件在工程湍流模擬應用中默認采用壁面函數方法對湍流邊界層進行模擬[1-2],壁面函數方法可以大幅放寬壁面第一層網格的尺度(通常30 基于對數定律的標準壁面函數已經被大量不可壓縮數值實驗確認,其中包括DNS模擬零壓力梯度邊界層和槽道流等結果。隨著近年DNS模擬能力的增強,涌現了大量可壓縮湍流邊界層DNS結果,其中文獻[4]使用DNS模擬了可壓縮低雷諾數槽道湍流,當馬赫數較小時標準壁面函數和DNS結果較為吻合,但是隨著馬赫數的增加基于不可壓流動的標準壁面函數和DNS之間的偏差逐漸增大。對于Ma2.48的槽道湍流,在黏性底層邊緣附近y+=10,相較于壁面參數,密度減小了50%,溫度增高了60%,表明低雷諾數超聲速槽道湍流存在強可壓縮性。 盡管壁面函數的研究工作已經持續開展了50多年,但其中大多數研究成果的應用工作并不樂觀,如壁面函數與用于全局流動問題模擬的湍流模型不相容的問題[5-6],容易引起數值模擬結果對壁面附近第一層網格節點位置的強烈依賴性,導致分離流動的數值模擬結果精度很差,因而提出了網格和流動自適應的壁面函數方法,保證在壁面函數有效的情況下對近壁流動物理特性進行恰當的分辨,特別是針對非平衡效應顯著的流動區域、逆壓梯度導致的流動分離和再附點附近區域,以獲得比較準確的氣動力/熱特性。此外,文獻[7]也針對壁面函數在RANS模擬中的應用問題開展了相關研究工作。 近年來可壓縮壁面函數的代表性工作,文獻[8]使用Crocco-Busemann方程,忽略壓力梯度的影響,將速度和溫度函數耦合起來,發展了適用于可壓縮湍流邊界層的壁面函數。國內壁面函數研究起步較晚,其中文獻[9-10]將文獻[8]中考慮流動可壓縮性和熱傳導的壁面函數耦合到了k-ω兩方程模型中;文獻[11]和文獻[12]分別通過數值實驗和風洞實驗對壁面函數的系數進行了修正研究;文獻[13]對文獻[8]中的壁面函數進行了修正研究。由于壁面律在存在逆壓梯度的復雜流動中是否適用無法確定[14-15],文獻[8]忽略對流項和壓力梯度影響的壁面函數對于分離點和再附點附近流動的模擬會存在困難。 除了標準壁面函數,由于近年來解析壁面函數[16]在壁面處不涉及太多假設,保留了邊界層方程中的對流項和壓力梯度項,因此在不可壓縮流體中已經得到應用。由于解析壁面函數在粗網格上的預測精度可以接近低雷諾數模型的結果,而計算時間比低雷諾數低一到兩個數量級。同時由于解析壁面函數在實際編程,計算中的魯棒性和可操作性等優點,都使得其工程應用得到廣泛關注。而將解析壁面函數用于可壓縮流體中時,由于需要考慮流體可壓縮性,其方法研究對于先進壁面函數在復雜超聲速和高超聲速流動中的應用也具有實際意義。本文基于OpenFoamV 5.0軟件平臺將目前應用于不可壓縮流動的解析壁面函數,通過可壓縮湍流邊界層控制方程的簡化,考慮密度變化、對流項變化和黏性耗散項對解析壁面函數的影響,探索其在可壓縮流動中的應用,并通過二維超聲速激波邊界層干擾算例進行驗證。 本文解算器使用Favre平均NS方程,無黏通量由Roe-Pike格式計算,黏性通量采用二階中心差分格式,時間推進采用一階歐拉格式。根據完全氣體假設,狀態方程為p=ρRT,空氣黏性系數使用Sutherland方程計算。壁面函數方法基于高雷諾數RANS模型,即標準k-ε模型。對于存在壁面的流動問題,局部雷諾數Rt=k2/ν/ε很小,黏性效應不能忽略,因此文獻[17]采用基于Rt的阻尼函數來計算近壁面湍流尺度,并在ε方程中添加Yap修正[18],來降低在分離流動中ε方程得到的近壁面湍流,即低雷諾Launder-Sharmak-ε模型。 在局部平衡湍流邊界層內,壁面定律為: (1) 其中:U+和y+定義為: (2) (3) (4) (5) 其中:常數cl=2.55,下標n表示壁面第一次網格面,如圖1所示。近壁面網格點P的壁面剪切應力為: (6) 解析壁面函數[16]在壁面附近通過可壓縮湍流邊界層假設簡化輸運方程,考慮對流項和壓力梯度的影響,壁面附近x-y平面上簡化的動量和能量方程為: (7) (8) 其中:P表示壓力;T表示溫度;μ和μt分別表示層流黏性系數和湍流黏性系數;Pr和Prt分別表示層流普朗特數和湍流普朗特數。湍流黏性系數為: μt=0 當y (9) (10) (11) 其中:C表示動量簡化式(7)中的壓力梯度和對流項。 (12) (13) (14) (15) (16) 湍動能方程中的在壁面附近生成項為: (17) 對于壁面附近的耗散項,在全湍流區為: (18) 在黏性底層內耗散項為: (19) 為了消除在黏性底層交界面處的間斷(圖1(a)),重新選取一個位置(使用下標d表示),令耗散項在壁面網格內連續分布(圖1(b)),需滿足條件: 圖1 耗散項在壁面網格內分布示意圖Fig.1 Schech map of dissipation term in the wall cell (20) 因此,在壁面網格內的平均耗散項為: (21) 對于壁面溫度的解析表達式可以通過類似于壁面速度的兩次積分得到,對于絕熱壁有: (22) 其中,Cth下標1表示黏性底層的值,2表示全湍流區的值: 等溫壁為: (23) 原始解析壁面函數詳情可見文獻[16]。 可壓縮流動的能量方程通常可表示為: (24) 式中:E表示總能,σ表示流體應力張量,q表示熱流。 為了增強壁面函數的魯棒性,本文發展的解析壁面函數和主網格的能量方程統一使用式(24),對于可壓縮湍流邊界黏性耗散項不能忽略[19],因此在解析壁面函數能量方程中需包含粘性耗散項。 湍流壁面函數方法使用粗網格進行數值計算,第一層網格壁面距離通常滿足20 (25) (26) 式(26)中右端第二項表示黏性耗散項,使用式(25)積分得到的解析速度計算,方程中的對流項和壓力梯度分別表示為: 上式D、C、Dth中下標1表示黏性底層的值,2表示全湍流區的值,在黏性底層內和全湍流區對簡化動量式(25)和能量式(26)積分,可得到解析速度和溫度表達式,具體形式如下: (27) (28) 其中: 系數N表示: 黏性底層溫度解析表達式為: (29) 其中: 全湍流區溫度解析表達式為: (30) 其中: 通過壁面第一層網格內的解析速度和溫度分布可以得到壁面剪切應力和壁面熱流。同時考慮到在使用粗網格求解時,為了更加準確描述主網格控制方程的黏性耗散項,即主方程中壁面網格內的平均粘性耗散項為: 在程序中通過解析速度表達式(27)、(28)數值求解。 本文使用斜射激波-湍流邊界層干擾來驗證發展的可壓縮修正解析壁面函數(MAWF),三種來流馬赫數實驗來流條件列于表1中[20-22]。來流邊界為充分發展的湍流邊界層,其邊界層厚度δ0和動量厚度θ0如表1所示,具有1.5%的自由來流湍流強度和黏性系數比率μt/μ=10。 表1 斜激波邊界層干擾來流條件Table 1 Inflow conditions for the impinging shock interactions 計算中使用結構網格,對于低雷諾數湍流模型,壁面第一層網格較密,第一層網格的y+≈1,對于高雷諾數湍流模型,第一層網格y+大約為30。為保證計算結果與網格無關,在開展結果對比之前,分別對表1中算例開展了網格無關性研究,計算結果表明所有算例均取得網格無關性結果,詳情可參考文獻[23],其中Ma=2.9算例標準壁面函數法粗網格結果如圖2所示,其中xI表示無黏性情況下斜激波入射位置坐標。 圖2 Ma=2.9斜激波邊界層干擾的網格收斂性研究Fig.2 Grid independency study for the Ma=2.9 impinging shock interaction 計算網格入口邊界的下部使用充分發展的湍流邊界層,入口邊界的上部使用無粘斜激波關系式得到的斜激波后參數,在壁面處,使用等溫無滑壁邊界條件,壁溫為Tw=271K。在頂部和出口邊界處,使用Neumann邊界條件。本算例密網格為200×90,粗網格為150×60。 圖3比較了10°和13°斜激波的壁面壓力、摩擦系數和壁面熱流,圖中湍流模擬方法分別為標準壁面函數(SWF)、原始解析壁面函數(AWF)、可壓縮修正解析壁面函數(MAWF)和低雷諾數Launder-Sharmak-ε模型(LS)。對于β=10°,所有模型均返回相似的壁面壓力,和實驗數據[20]吻合。從摩擦系數結果來看,在無粘激波反射點附近存在一個小的分離區。LS模型的結果與實驗結果非常接近,壁面函數不能復現分離區,其中SWF傾向于低估分離區上下游的摩擦系數。壁面熱流不同模型的結果差異較大,其中MAWF結果更接近于密網格LS模型。對于β=13°,所有模型預測的壁面壓力和摩擦系數結果與實驗值較為吻合,MAWF預測的壁面熱流和密網格LS模型較為接近,而SWF和AWF均不能準確預測壁面熱流,在分離區前后甚至出現熱流符號相反的現象。 圖3 Ma=2.9算例不同入射角壁面壓力(上)、摩擦系數(中)和壁面熱流(下)Fig.3 Wall pressure(top),skin-friction(middle) and wall heat-flux(bottom) distribution for the Ma=2.9 case with different impinging angles 本算例網格類似于Ma=3.0算例,其入口邊界使用充分發展的可壓縮湍流邊界層,其中動量厚度如表1所示,在壁面處使用等溫無滑壁邊界條件,壁溫為Tw=300 K。本算例密網格為240×80,粗網格為120×45。在相同設置的情況下,不同湍流模擬方法消耗的計算機時間對比如圖4所示,通過對比表明使用粗網格的壁面函數將大幅減少計算時間,僅為密網格低雷諾數模型計算時間的5%左右,一是由于網格量大幅減少,二是由于壁面距離的增加,在相同CFL數時計算時間步長的增加,收斂速度加快。 圖4 Ma=5.0算例不同模型計算消耗時間對比Fig.4 The CPU time comparison using different turbulence models for the Ma=5.0 case 圖5比較了不同入射角的壁面壓力、摩擦系數和壁面熱流,從圖中可知四種數值模擬方法得到的分離區較試驗結果[21]較小。當激波邊界層干擾加強時,AWF得到的壁面摩擦系數和Stanton數在分離起始位置出現非物理振蕩,主要原因是AWF使用壁面第一個網格點信息計算對流項,如式(11),由于分離區附近流向速度變化較大,對流項在整個壁面網格內取常數,將導致AWF預測能力降低。而MAWF認為對流項在壁面處為零,以無量綱壁面距離的平方項遞增,從物理上更符合邊界層內流動規律,從而提高預測精度。對于三種不同角度斜激波,MAWF相較于AWF,壁面熱流的預測能力大幅上升,主要得益于能量方程簡化中保留了黏性耗散項,使得粗網格預測的壁面熱流精度大幅改善,接近密網格LS的結果。 本算例由于激波生成器拐角處的膨脹波會對下表面產生影響,因此在數值模擬的過程中加入了激波產生器的固壁邊界,激波產生器夾角β=7.5°和15°,且由于本算例風洞試驗模型是軸對稱體,因此z方向按照試驗外形旋轉2°,其余邊界設置和Ma=2.9和Ma=5.0算例相同,壁面溫度為300K。本算例密網格為420×105,粗網格為280×40。 圖6給出了四種不同湍流模型的數值結果與試驗值[22]的對比,其中MAWF大幅度提升了壁面熱流的預測精度,在分離區前后得到和密網格LS模型相同的結果,且避免了AWF在分離區起始位置附近的非物理振蕩。和實驗值相比,數值結果高估了分離區的大小和分離區內的壁面壓力、摩擦系數和壁面熱流,這主要是RANS模型的局限性導致,文獻[24]總結了不同RANS模型預測的β=15°壁面熱流結果,所有模型均出現高估分離區熱流的情況。 圖6 Ma=7.2算例不同入射角的壁面壓力(上)、摩擦系數(中)和壁面熱流(下)Fig.6 Wall pressure(top), skin-friction(centre) and Stanton number (bottom) distribution for the Ma=7.2 case with different impinging angles 本文通過可壓縮湍流邊界層特點,考慮邊界層內密度的變化,將基于不可壓縮流動的解析壁面函數推廣到可壓縮流動原始解析壁面函數(AWF),并考慮邊界層內對流項變化和粘性耗散項的影響,構造了適用于可壓縮修正的解析壁面函數(MAWF),通過三個不同來流馬赫數的斜激波邊界層干擾算例進行測試,并與LS和SWF進行了比較。主要結論如下: 1)整體來看四種數值模擬方法預測的壁面壓力差異不大,且與實驗吻合良好。 2)整體來看四種數值模擬方法預測的壁面摩擦系數差異不大,標準壁面函數預測的數值偏小,可壓縮解析壁面函數由于考慮了對流項在邊界層內分布,消除了原始解析壁面函數在分離區起始位置的非物理振蕩。 3)壁面熱流的數值結果差異較大,整體來看本文構造的可壓縮解析壁面函數得到的結果和密網格Launder-Sharmak-ε模型結果最為接近,而原始解析壁面函數和標準壁面函數,不能準確預測壁面熱流。 4)壁面函數模型使用粗網格,相較于低雷諾數模型可以大幅減少計算時間,對于Ma=5算例,計算時間約為Launder-Sharmak-ε模型的5.3%,而相較與標準壁面函數僅增加了1%左右的時間。 總的來說,四種方法都顯示出良好的壁面壓力和摩擦系數預測能力。然而,標準壁面函數和原始解析壁面函數嚴重低估壁面熱流,即使在分離區前后其結果也和密網格Launder-Sharmak-ε模型結果相差甚遠。本文構造的解析壁面函數充分考慮可壓縮湍流邊界層流動的特征,彌補了原始解析壁面的缺點,從而大幅提升了壁面熱流的預測精度,且不需要在近壁面區域內的精細網格。1 物理模型
2 壁面函數
2.1 標準壁面函數(Standard Wall Function)
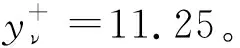
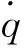
2.2 解析壁面函數(Analytical Wall Function)



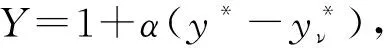
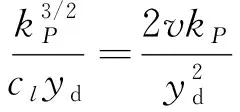
2.3 可壓縮修正(Modification of AWF)
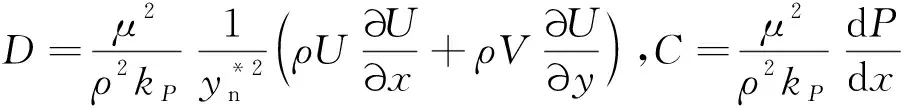
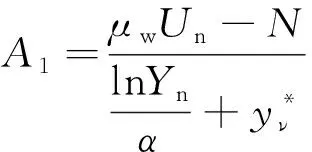
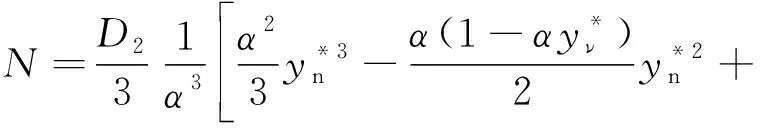


3 數值結果


3.1 Ma=2.9斜激波邊界層干擾[20]

3.2 Ma=5.0斜激波邊界層干擾[21]

3.3 Ma=7.2斜激波邊界層干擾[22]
4 結 論

