基于LS-SVM的結構損傷識別仿真分析
羅麗燕 王添龍
(1廣東省建筑設計研究院有限公司;2東莞市路橋投資建設有限公司)
基于LS-SVM的損傷識別,借助LS-SVM lab工具箱,主要使用分類和回歸函數對結構進行損傷識別。LS-SVM損傷識別方法流程圖如圖1。
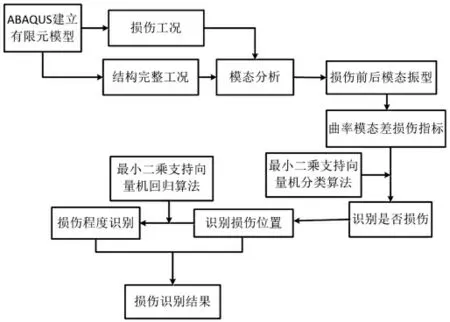
圖1 LS-SVM的損傷識別流程
1 曲率模態損傷識別理論
梁的振動微分方程為:
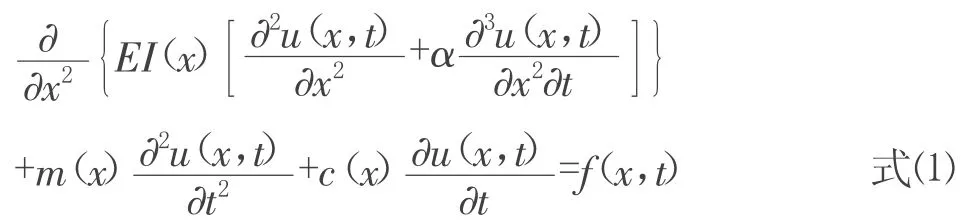
其中,u(x,t)表示t時刻在x處的橫向振動位移,m(x)表示單位長度梁的質量,α是剛度系數。
式⑴的簡諧運動形式為:

其中U(x)為振型函數,與位置有關;T(t)為簡諧運動函數,與時間有關。
將式用各階位移模態φi(x)來表示[1,4]:

其中qi(t)表示模態坐標。
由文獻[12]知梁振動的微分方程的解為:
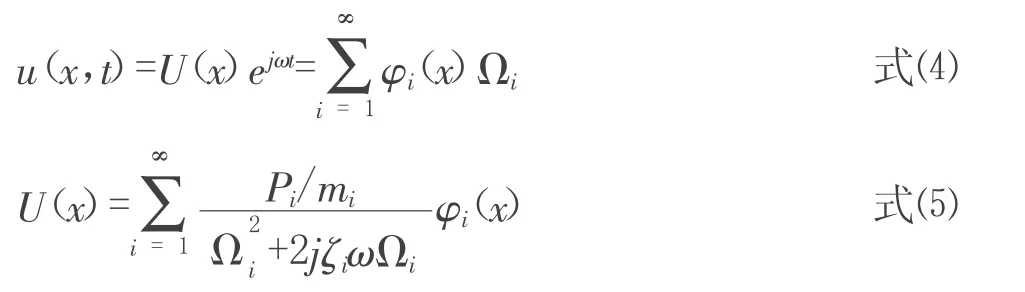
則由曲率的定義可得:
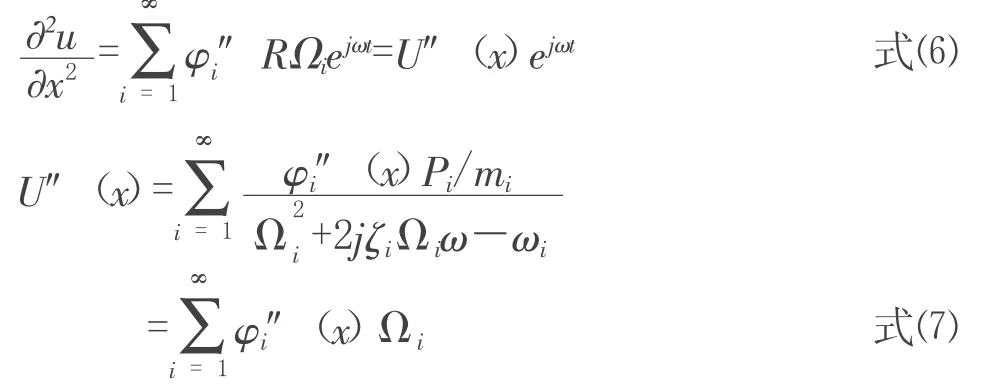

其中,φi表示各階位移模態,Δl為相鄰兩測點間的距離。
曲率模態差是結構損傷前后曲率模態值的差的絕對值[11],公式如下:

2 LS-SVM原理
LS-SVM作為SVM的一種改進算法,它提高了SVM的分類正確率,彌補了SVM在某些方面的不足。所以推廣LS-SVM的研究應用很有必要[3]。已知一組訓練集:
(x1,y1),…,(xl,yl),x∈Rn,y∈R對于非線性問題,可以用非線性變換φ(.)將輸入向量映射到高維特征空間,轉化為類似的線性回歸問題。LS-SVM最小化目標函數為:

其中,w為權向量;γ為正則化參數;ei為樣本訓練誤差。
用拉格朗日法求解:
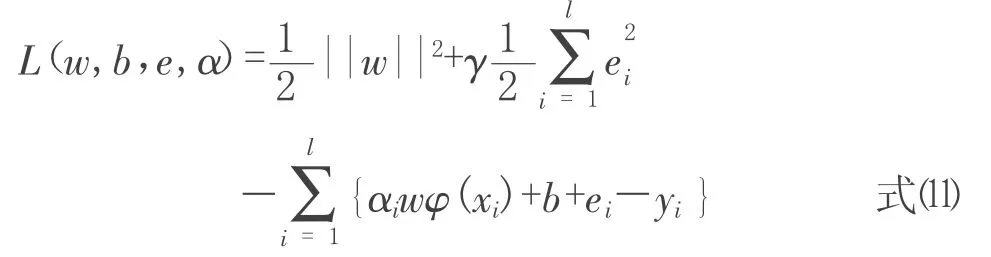
其中αi(i=1,2,…,l)是拉格朗日乘子。對w,b,ei,αi求偏導,根據優化條件,可得到:

其中,αi=γei,wφ(xi)+b+ei-yi=0
定義核函數K=(xi,yi)=φ(xi)·φ(xj)是滿足條件的對稱函數。根據文獻[5],優化問題轉化為求解線性方程:
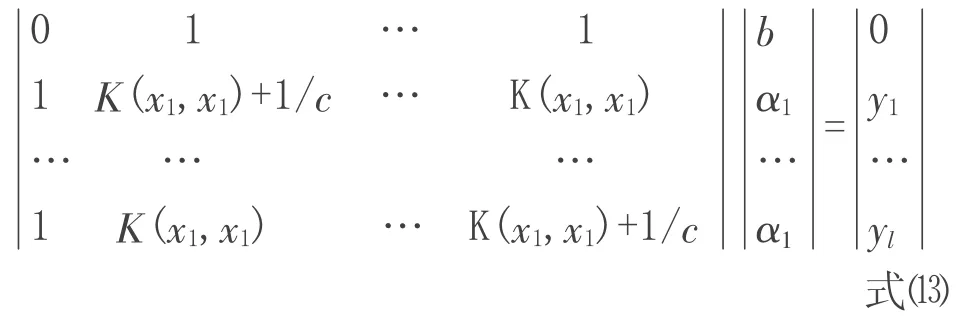
最后用最小二乘法求出α和b得到LS-SVM回歸函數為:

K(x,xi)=?(xi)·?(x)稱為核函數,在本文中選擇的是RBF函數。
RBF函數(徑向基核函數):

和SVM一樣,LS-SVM使用核函數K(x,xi)代替高維空間的內積形式可以解決高維計算問題[6]。
3 鋼桁架數值模擬分析
用一長度為2.5m,寬度和高度均為0.5m的空間鋼桁架作為有限元分析模型。結構及結構損傷桿件編號如圖2所示。
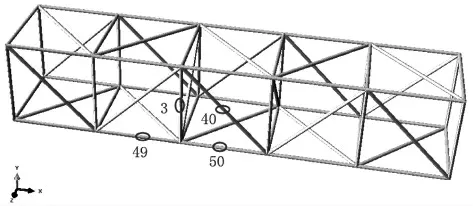
圖2 模型及損傷桿件編號
該結構共有66根桿件,分成66個單元,使用彈性模量折減的方式模擬桿件損傷。根據相關計算分析,輸出結構的模態頻率和振型,算出結構的曲率模態差值,一共有三種損傷類型,6種損傷工況,損傷工況如表1所示。

表1 損傷工況
3.1 損傷位置識別結果
利用LS-SVM分類算法和回歸算法分別實現損傷位置和損傷程度識別功能,針對各損傷工況,進行損傷位置識別時,采用各工況發生損傷程度為10%、15%、20%、30%、35%、40%、50%、60%、70%的樣本作為LS-SVM的訓練樣本,以損傷程度為25%、45%、65%的樣本作為LS-SVM的測試樣本,算出結構在三種不同損傷位置類型下不同損傷程度的模態曲率差值,作為LS-SVM的輸入參數,結構的損傷位置作為LS-SVM的輸出參數。構造好訓練樣本和測試樣本后即可使用LS-SVM對訓練樣本進行分類,檢驗LS-SVM對結構損傷位置的識別能力。其損傷識別結果如表2所示。

表2 損傷位置識別結果
3.2 損傷程度識別結果
在建立的LS-SVM模型基礎上,可對損傷工況出現25%、35%、55%、65%的損傷程度進行預測,進行損傷程度識別時,以結構各工況發生損傷程度為10%、15%、20%、30%、35%、40%、50%、60%、65%、70%、75%的 樣 本 作 為LS-SVM的訓練樣本,以發生損傷程度為25%、45%、55%、65%的樣本作為LS-SVM的測試樣本,其程度損傷識別結果如表3所示。
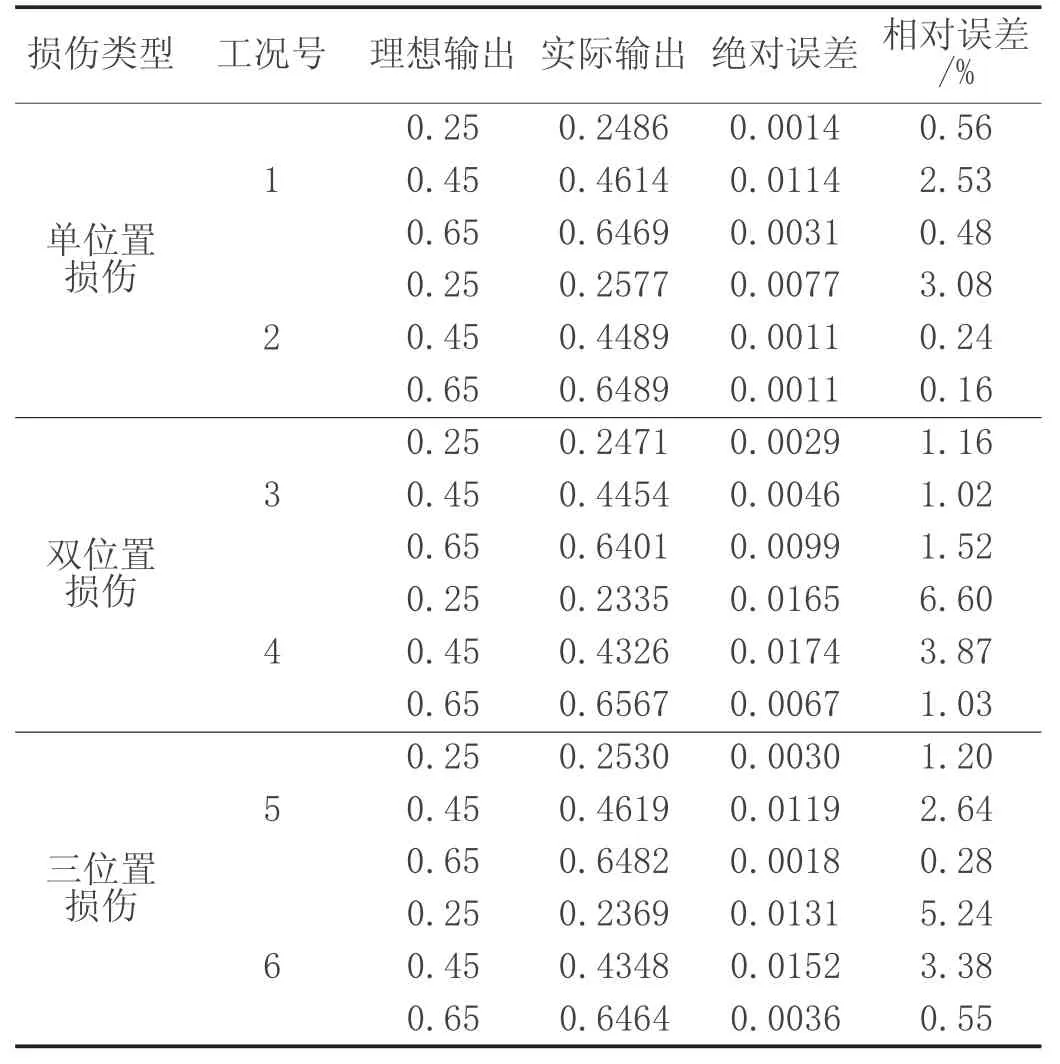
表3 損傷程度識別結果
4 結論
通過建立一個空間鋼架的有限元模型,用LS-SVM的分類和回歸模式識別方法對結構進行了損傷識別,均取得良好的識別結果。可得出以下結論:
⑴使用LS-SVM的分類算法和回歸算法對模型算例進行損傷識別,說明了LS-SVM具有很好損傷定位和損傷程度識別效果。
⑵LS-SVM與模態分析方法與LS-SVM有機結合,可準確地對結構進行損傷位置的定位和損傷程度的識別,還可以有效地識別出結構同時發生單位置、雙位置、甚至多位置處的多處不同程度損傷的損傷位置和損傷程度。

