巧借函數圖像 解答數學難題
吳作成
(福建省石獅市第一中學 362700)
函數知識在高中數學中有著重要的地位,是學生學習中的重點和難點,也是高考中的必考內容.在高中數學解題中,傳授學生解題技巧,靈活利用函數圖像分析解題思路,提高學生解題效率.函數圖像作為函數的重要表現方式,其價值和作用非常大,借助函數圖像引導學生直觀解題,節約學生解題時間,同時,利用函數圖像分析問題,可以簡化解題步驟,幫助學生更好的解題.因此,在高中數學解題教學中,讓學生巧妙利用函數圖像,體會數形結合思想,加強學生綜合能力培養.
一、借助函數圖像,掌握解題技巧
高中數學解題中,需要學生掌握一定的解題技巧,解決相應的數學難題.在函數知識學習中,函數圖像解題是一種有效的解題方式和技巧,根據題目意思畫出函數圖像,通過對圖像進行觀察和分析,找出其中的數量關系,達到快速解題的目標.特別是在一些選擇題和填空題.
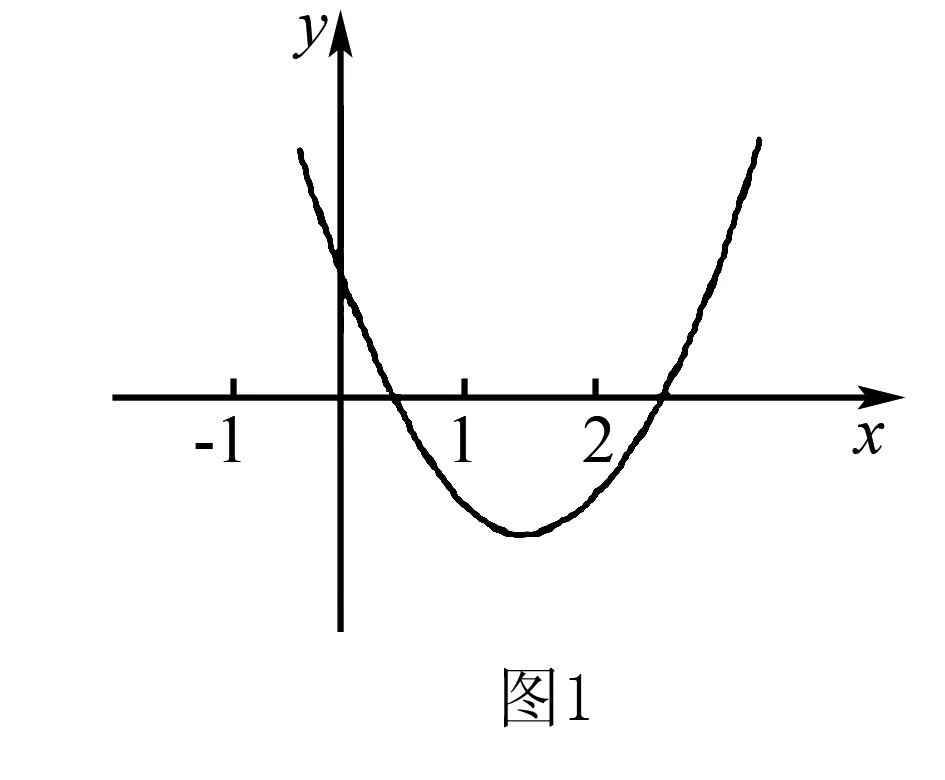
例題已知二次函數y=ax2+bx+c的圖像如圖1所示,判斷下列代數式值的正負.①a+b+c②a-b+c.
在解題時,引導學生從函數圖像入手,觀察函數圖像的開口方向、特殊交點,通過這樣可以判斷出a>0.在對兩個代數式進行判斷時,教師可以利用特殊值代入的的方式,幫助學生完成解題.當x=1時,那么y=a+b+c,,當x=-1時,那么y=a-b+c,根據這樣可以找出其在函數圖像中的坐標位置,如(1,a+b+c)、(-1,a-b+c).通過對圖像進行觀察,可以非常清晰的看到,x=1時,y<0,x=-1時,y>0,做出準確的判斷.因此,高中數學教學中,教師需要利用函數圖像解題,引導學生開展更多練習,找到更加有效的解題方式,提高學生的解題能力性,從而保證學生的解題效果和質量.
二、借助函數圖像,加深數學思想體驗
利用函數圖像是高中數學解題中的重要方式,在數學問題中,其條件是通過數字和圖形展示的,數與形之間有著密切的關系.高中數學解題教學中,培養學生函數圖像應用思維,結合具體圖像進行分析,完成數學難題解答.借助函數圖像分析問題關鍵點,減少解題運算過程,為學生指明解題思路.同時,利用函數圖像解題是數形結合思想的重要表現.
例題已知函數y=x2+x+a中,當x∈[-1,2]時,函數的最值之和是6,求解a的值.

三、利用函數圖像,開展分類討論
高中數學解題中,利用函數圖像對問題進行分析,找到題目中的障礙和迷惑點,準確把握解題關鍵點,完成數學問題思考和解答.在實際的解題中,要求學生根據函數表達式,準確畫出函數圖像,如果題目中存在多個函數表達式,需要采取分類討論活動,討論未知量的取值對函數結果的影響,進而完成數學題目的解答.
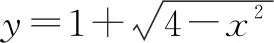

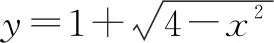
四、利用函數圖像,優化解題方式
高中數學解題教學中,數學題目復雜多變,具有靈活性特點,面對相同的題目,學生可以采取不同的解題方式,雖然可以得到相同的答案和結論,但是,學生的計算量和計算步驟差異較大.利用函數圖像解題,其本質就是借助數形結合思想進行解題,借助圖像將問題展示出來,培養學生良好的作圖習慣,利用函數圖像尋找最佳的解題方式,保證學生數學解題質量.
例題求解滿足不等式|x-5|-1<|2x-3|的x的取值范圍.
在解題的過程中,在去絕對值時,常常會出現一些問題,使得學生解題結論不準確或者不全面等問題.為了幫助學生解題,教師可以將不等式左右兩邊分別轉化成函數y=|x-5|-1和y=|2x-3|,然后畫出相應的函數圖像,通過對函數圖像進行觀察和分析,可以非常清晰地找到不等式成立的情況,即函數y=|x-5|-1的圖象在函數y=|2x-3|的下方.通過這樣的方式進行解題,可以簡化學生解題步驟,提高學生的解題效率,優化學生的解題方式,提高學生的解題能力.
五、利用函數圖像,轉變解題方向
學生在初中數學學習時已經接觸函數知識,了解一些初等的函數類型和知識,是學生高中函數知識學習基礎.高中數學解題教學中,函數知識學習的最終目的是解決實際問題,根據問題構建相應的數學模型,將函數圖像作為數學問題解題工具.作為高中數學教師,應當引導學生靈活利用函數圖像,明確數學問題的解題方向,完成數學問題的思考和解答.
例題求解不等式|x+2|-|x|>-1.
一般來說,學生在解題時,常常會想到對不等式進行移項、平方,然后開根號進行處理,雖然可以解決題目,但是,隨著不等式問題的復雜,此種解題方式使得解題過于復雜,影響學生解題效率.結合常規思路的思考,開展相應的討論活動,引入相應的函數圖像.在解題中,對不等式進行移項,轉化成|x+2|>|x|-1,構建相應的函數,畫出相應的函數圖像,對其進行觀察和分析,找出函數的交點,完成不等式問題的思考和解決.
高中數學教學中,不僅僅要求學生掌握數學知識,還需要學生掌握解題方法,結合相應的習題訓練,不斷歸納和總結解題技巧,更好的解決數學難題.

