兩個指數型函數在解題中的應用舉例
蘇藝偉
(福建省龍海第一中學新校區 363100)
函數y=ax+a-x(a>0且a≠1)以及y=ax-a-x經常出現在高三年級的模擬試題當中,掌握好這兩個函數的相關圖像,性質能夠幫助我們更好地解決數學問題.
一、知識鏈接
1.y=ax+a-x(a>0且a≠1)

函數y=ax+a-x(a>0且a≠1)圖象如圖1所示,該函數是一個偶函數,最小值為2,在(-∞,0)單調遞減,在(0,+∞)單調遞增.
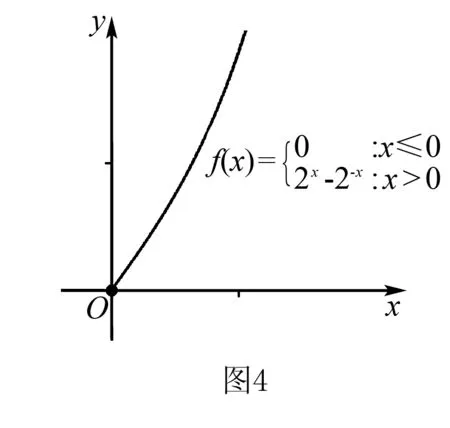
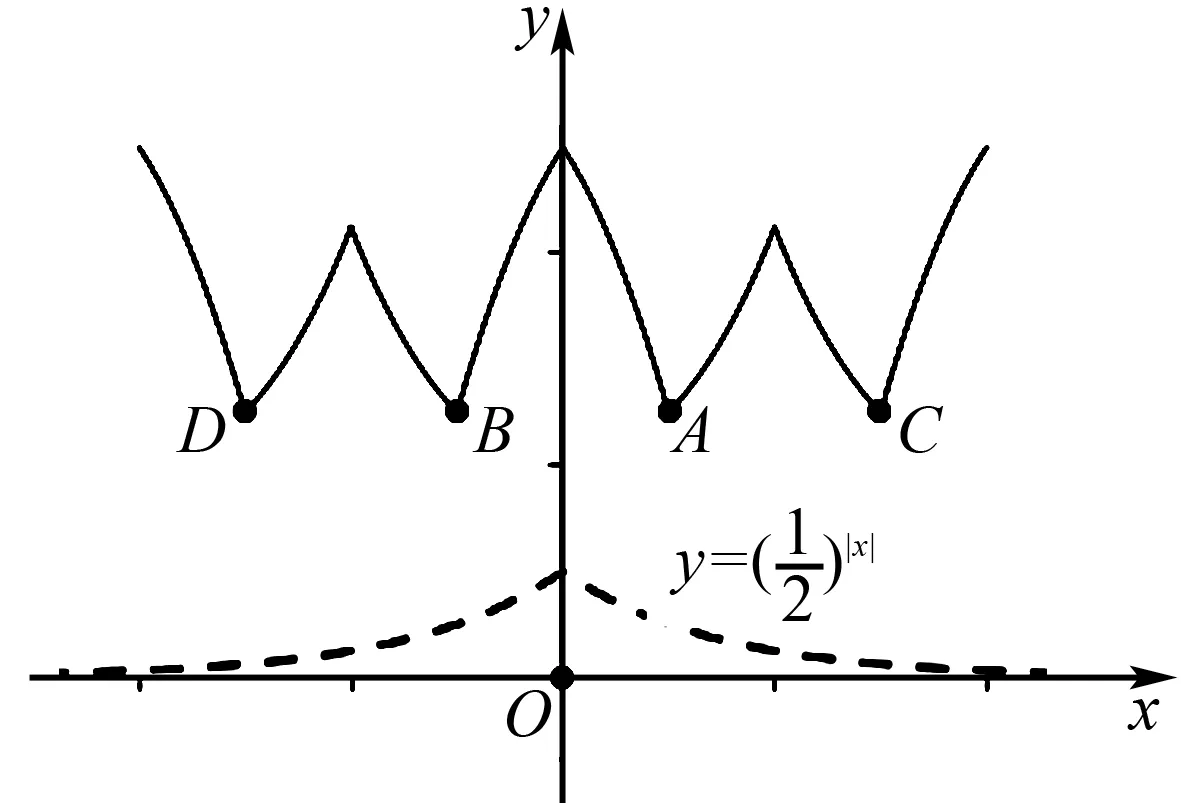
2.y=ax-a-x(0 函數y=ax-a-x(0 3.y=ax-a-x(a>1) 函數y=ax-a-x(a>1)圖象如圖3所示,該函數是一個奇函數,圖像經過點(0,0),在R單調遞增. 對于上述函數模型,最經常出現的是a=2,a=e的情形,有些時候還會出現由上述函數模型經過左右平移而得到的新函數.在實際解題中,應該抓住這三個基本的函數模型,以不變應萬變,靈活應用,正確解答. 例1下列函數中,圖像關于原點對稱且單調遞增的是( ). A.f(x)=sinx-xB.f(x)=ln(x-1)-ln(x+1) A.(-∞,-1)∪(2,+∞) 例3已知函數f(x)=x2(2x-2-x),則不等式f(2x+1)+f(1)≥0的解集是( ). 解析易知f(-x)=-f(x),所以f(x)為奇函數.又f′(x)=2x·(2x-2-x)+x2(2x+2-x),當x>0時,f′(x)>0,因此f(x)在(0,+∞)上單調遞增.由于f(x)為奇函數,所以f(x)在R上單調遞增.f(2x+1)+f(1)≥0?f(2x+1)≥-f(1)?f(2x+1)≥f(-1)?2x+1≥-1?x≥-1.故不等式f(2x+1)+f(1)≥0的解集是{x|x≥-1}. 圖5 例5已知函數f(x)=ex-e-x-2x, (1)討論f(x)的單調性; (2)設g(x)=f(2x)-4bf(x),當x>0時,g(x)>0,求b的最大值. 解析(1)f′(x)=ex+e-x-2≥0,f(x)在R上單調遞增. (2)g(x)=e2x-e-2x-4x-4bex+4be-x+8bx g′(x)=2(ex+e-x-2)(ex+e-x-2b+2) 令h(x)=ex+e-x-(2b-2) 若2b-2≤2,即b≤2時,h(x)>0,g′(x)>0,g(x)在(0,+∞)上單調遞增,g(x)>g(0)=0,符合題意. 綜上有b≤2,因此b的最大值為2. 例6已知函數f(x)=x2-2x+a(ex-1+e-x+1)有唯一零點,求a的值. 例7已知函數f(x)=ex-a+e-x+a,若3a=log3b=c,則( ). A.f(a) C.f(a) 解析由于f(2a-x)=e-x+a+ex-a,因此f(2a-x)=f(x),所以f(x)的圖像關于直線x=a對稱且f(x)在(a,+∞)上單調遞增.由圖6可知,a 因此f(a) 例8設f(x)=-x2+2x-2(ex-1+e1-x),則使得f(x+1) 解析由于f(2-x)=f(x),故f(x)圖像關于直線x=1對稱,因此f(x+1)圖像關于直線x=0對稱.令g(x)=f(x+1)=-x2+1-2(ex+e-x),則g(x)為偶函數且在(0,+∞)上單調遞減. f(x+1) 例9已知函數f(x)=emx+e-mx+x2-mx的圖象在點A(x1,f(x1)),B(-x1,f(-x1))處兩條切線的交點P(x0,y0)一定滿足( ). A.x0=0 B.x0=mC.y0=0 D.y0=m 解析由f(x)=emx+e-mx+x2-mx得f′(x)=memx-me-mx+2x-m.點A(x1,f(x1))處的切線方程為y-f(x1)=f′(x1)(x-x1);點B(-x1,f(-x1))處的切線方程為y-f(-x1)=f′(-x1)(x+x1);又點P(x0,y0)滿足以上兩式,所以y0-f(x1)=f′(x1)(x0-x1),y0-f(-x1)=f′(-x1)(x0+x1);兩式相減得f(-x1)-f(x1)=x0[(f′(x1)-f′(-x1))]-x1[(f′(x1)+f′(-x1))],又f(-x)-f(x)=2mx,f′(x)+f′(-x)=-2m,所以2mx1=x0[(f′(x1)-f′(-x1))]+2mx1,故x0=0. 不難發現,以函數y=ax+a-x(a>0且a≠1)和y=ax-a-x為載體的試題,常融入函數的對稱性,單調性,零點,最值等于一體,結合圖像,不等式,導數等重要知識點,體現了高考評價體系提出的基礎性,綜合性,應用性,創新性的要求.試題雖然簡短但卻閃耀著智慧的光芒.在實際解題中,要抓住這兩個最基本的模型,由它們出發引申出一系列的變式,進而掌握好此類題型. 練習1已知函數f(x)=x2-4x+(m2-m)(ex-2+e-x+2)有唯一零點,則m的值可以是____. 解析由于y=x2-4x和y=ex-2+e-x+2對稱軸都是x=2,所以f(x)的對稱軸是x=2.故令f(2)=0得m=2或m=-1. 練習2已知f(x)=ex-1-e1-x+x,則不等式f(x)+f(3-2x)≤2的解集是____. 解析由于f(x)+f(2-x)=2,所以不等式f(x)+f(3-2x)≤2,即為f(x)+f(3-2x)≤f(x)+f(2-x),即f(3-2x)≤f(2-x),又f′(x)>0,f(x)單調遞增,所以3-2x≤2-x,x≥1.故解集為{x|x≥1}. 練習3已知函數f(x)=x2-4x-1+ex-2+e-x+2有兩個零點,則x1+x2=____.二、基礎應用

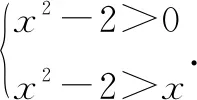
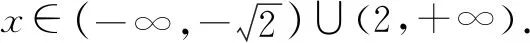



三、拓展應用