一道北京市數學競賽預賽試題模型本質與多解探析

余業兵 蔣中海

(西南大學附屬中學校 400700)

當我們解決一道新題目時，G·波利亞告訴我們較好的想法是這樣的： “你見過同樣的題目以一種稍有不同的形式出現嗎？”，“你知道一道與它有關的題目嗎？”， “你能利用它嗎？你能利用它的結果嗎？你能利用它的方法嗎？”.有時候有些題目具有一定的代表性，我們可以發現一類本質屬性與它相關、相似或者是相近的一類題目，我們把這樣的題目叫做這一類題目的模型，有的也把它稱作是這一類題目的母題，如果我們能夠深刻理解模型題(母題)的本質屬性或者關鍵屬性，遇到的相關題目也就迎刃而解了.本文基于這樣的解題思路，就一道數學競賽預賽壓軸題的母題模型、模型本質、解題視角、各種解法做深入的探究與分析.

一、題目呈現

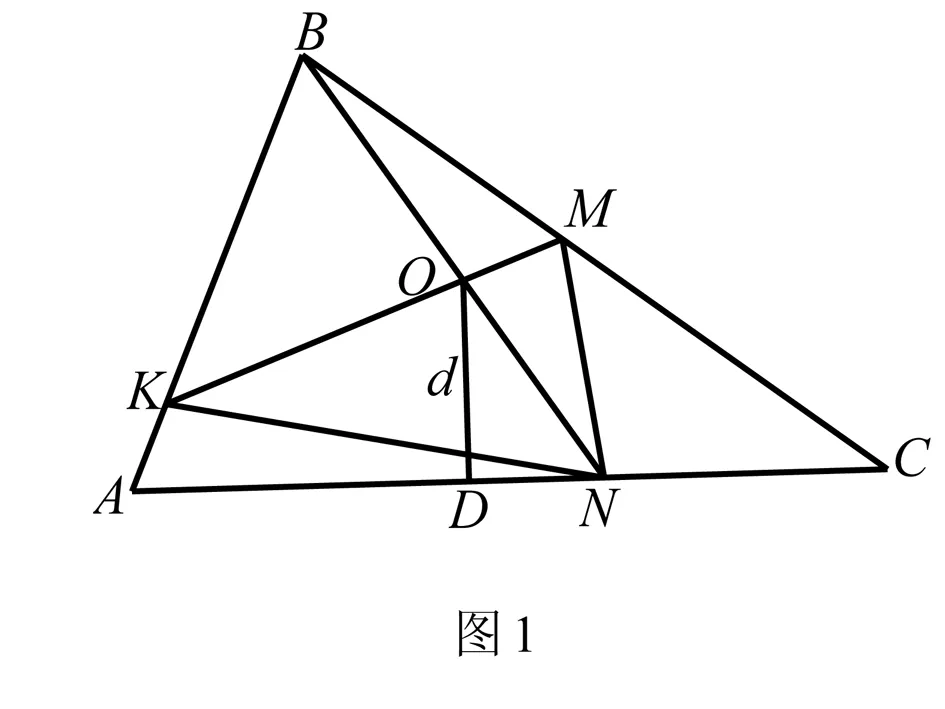
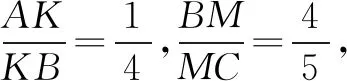
題目分析題目考查學生認識圖形、分析圖形，綜合運用所學知識解決圖形中線段比例、三角形面積等相關問題的能力，考慮到是最后一個題，命題者故意做了一定的偽裝，穿了幾件衣服，顯得較為新穎，有一定的難度.幾何題的關鍵在于認清典型圖形與圖形之間的關系，通過細致分析不難發現題目中圖形關系的關鍵在于“點O分BN成的比和點N分AC成的比是確定的”，找到這個關鍵后再思考我們見過與它相關、相似或者是相近的題目嗎？通過仔細分析，我們發現下面這個典型常見模擬題與本題的關鍵要素是相近的，圖形關系本質上是一致的.

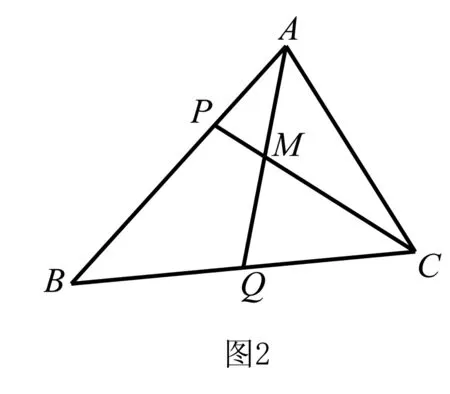
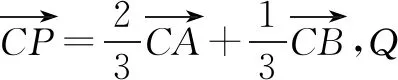
模型分析該題是一道傳統的向量題，可以采用經典解法“封閉圖形加基底表示”或者“三點共線的充要條件”，而它又是一道幾何題，故既可以利用平面幾何中處理線段比例的常見方法(平型切割或者梅勞定理)，也可以采用解析幾何中用坐標表示的方法(由于和目標題目解法想通，就不具體分析了，留給讀者自己分析).而目標試題顯然與模型試題圖形本質上是一致的，再加上三角形中面積的不同處理方法，各種解法也就任性而自然地生成了.

二、解法探析

1.平面幾何視角

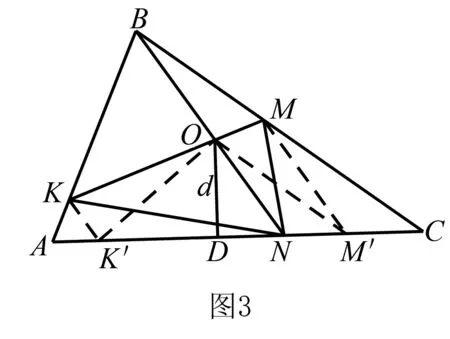
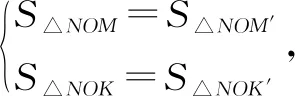
解法三(面積公式)我們可以采用不同的方法計算面積，其它的同解法一、解法二.

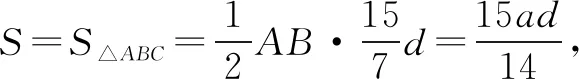
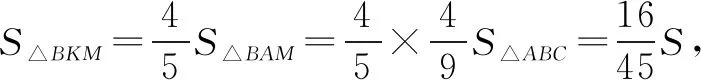
解法點評先從平面幾何的視角來看，對付線段比例問題最常用的方法是“平行切割”，就像解法一那樣，只要作出適當的平行線，利用圖形中被平行線所截得的對應線段成比例就可以了，解法常規、簡潔優美；除了這種方法，競賽中也可以選擇“梅涅勞斯”定理這個對付線段成比例的通法，就像解法二那樣重復使用“梅涅勞斯”定理可以輕松解決，思路單一而簡潔；解法四采用了面積法，更是別有一番風味，讓人眼前一亮.再有就是可以采取不同的面積的處理方式，解法一中的處理顯得巧妙而簡單，解法二、四中的處理都是常用面積處理方法.

2.平面向量視角

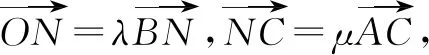
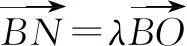
解法點評向量作為一個好用的工具，在處理幾何問題和代數問題上都有廣泛的應用，解法五、解法六中向量常見的運算意識，基底意識、三點共線模型意識、封閉圖形意識、待定系數意識都得到了充分的應用，具有一定的代表性.

3.解析幾何視角

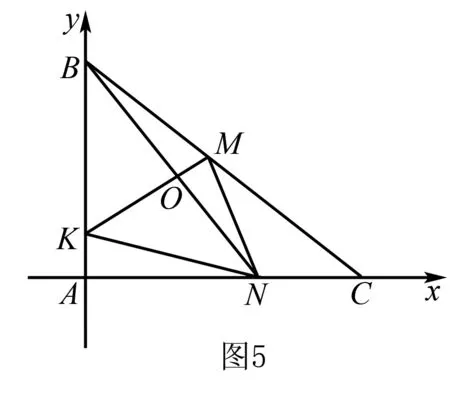
解法七(坐標法)如圖5，考慮到這是一道填空題，而 “點O分BN成的比和點N分AC成的比”不會因為三角形形狀的改變而改變，也就保證了圖形中的三角形面積比例不會發生改變，只要保證“AC=a，OD=d”這個條件，就可以把三角形特殊化，不妨讓AB⊥AC，以AB、AC分別為x、y軸建立平面直角坐標系，則C(a,0)，設B(0,b)，由易得由易得再結合可求得這就求出了于是直線令y=0可得：這就求出了至于求面積既可以回到解法二、解法三，也可以算弦長和點到直線的距離，只需要讓就行了.

解法點評解析的精髓在于利用代數計算的方式解決幾何問題，使用時恰當坐標系的選取尤其重要，解法七巧妙地利用了圖形特殊化后“線段比例”不會改變、面積比列也不改變這兩個事實，實現了小題小解、小題巧解.

三、解后反思

頓悟絕非空隙來風，巧解也不會憑空產生，解題思維的產生往往是新的刺激信息與以往解題經驗在大腦中綜合作用的結果，要想解題得法、解得有法、解答多法，就需要我們在日常的教學與學習中注意總結、多多積累，吃透題目模型的本質屬性，厘清各種數學要素的相互關系，把握解題的關鍵鑰匙，這樣，在遇到一道新的題目時，由于“模型本質心中藏”，也就自然而然“解法由我不由天”了.