從“以方測(cè)圓”到“化曲為直”
張敏

摘要:在數(shù)學(xué)教學(xué)中融入數(shù)學(xué)史,可以把教材中呈現(xiàn)的素材和相關(guān)史料以知識(shí)發(fā)生、發(fā)展過(guò)程的視角進(jìn)行合理重組,促進(jìn)學(xué)生理解數(shù)學(xué)本質(zhì),領(lǐng)會(huì)數(shù)學(xué)思想,感悟數(shù)學(xué)文化。HPM取向的《圓的面積》教學(xué),結(jié)合史料,依循人類(lèi)探索圓的面積的發(fā)展過(guò)程,以學(xué)生已有的經(jīng)驗(yàn)為依托,引領(lǐng)學(xué)生“以方測(cè)圓”,建立圓面積和正方形面積(r2)的聯(lián)系;運(yùn)用數(shù)方格法“數(shù)”出圓的面積,初步體會(huì)極限思想;運(yùn)用“切西瓜”法“化曲為直”,推理論證。
關(guān)鍵詞:HPM;數(shù)方格;化曲為直;極限;《圓的面積》
HPM(History and Pedagogy of Mathematics),通常被理解為“數(shù)學(xué)史向數(shù)學(xué)教學(xué)的滲透”。HPM相關(guān)研究表明,個(gè)體的認(rèn)識(shí)過(guò)程與人類(lèi)的認(rèn)識(shí)過(guò)程基本是一致的,在數(shù)學(xué)教學(xué)中融入數(shù)學(xué)史,可以把教材中呈現(xiàn)的素材和相關(guān)史料以知識(shí)發(fā)生、發(fā)展過(guò)程的視角進(jìn)行合理重組,促進(jìn)學(xué)生理解數(shù)學(xué)本質(zhì),領(lǐng)會(huì)數(shù)學(xué)思想,感悟數(shù)學(xué)文化。《圓的面積》一課,筆者結(jié)合相關(guān)史料,開(kāi)展了HPM取向的教學(xué)實(shí)踐。
一、教學(xué)準(zhǔn)備
(一)“圓的面積”相關(guān)史料
最初,人們認(rèn)為,圓比較近似正方形,求圓的面積,可以想辦法作出一個(gè)正方形,使它的面積恰好等于圓的面積。但無(wú)論是外切正方形還是內(nèi)接正方形,都不能滿足這個(gè)要求。這曾是困擾古希臘數(shù)學(xué)家的三大幾何難題之一。
我國(guó)古代數(shù)學(xué)家劉徽和祖沖之,從圓的內(nèi)接正六邊形出發(fā),讓邊數(shù)成倍增加,單側(cè)逼近圓的面積;古希臘數(shù)學(xué)家阿基米德,則從內(nèi)外兩個(gè)方向雙側(cè)逼近圓的面積。這些“以方測(cè)圓”思路中的“逼近”就是試圖接近“極限”。
古印度數(shù)學(xué)家則采用“切西瓜”的辦法:把圓切成許多“小瓣”,再把這些“小瓣”平均分成兩部分,各自展開(kāi)后,拼插成一個(gè)近似的平行四邊形,用這個(gè)近似平行四邊形的面積去代替圓的面積。后來(lái),德國(guó)天文學(xué)家開(kāi)普勒也仿照“切西瓜”的方法,大膽地設(shè)想把圓分割成無(wú)窮多個(gè)小扇形,圓的面積就是無(wú)窮多個(gè)小扇形面積的和。開(kāi)普勒斷言(但無(wú)法證明):無(wú)窮小的扇形可以看作三角形,扇形面積等于三角形的面積。顯然,這種方法對(duì)人類(lèi)的想象和推理提出了挑戰(zhàn),是極限思想的雛形。
(二)HPM取向的《圓的面積》教學(xué)思路
盡管歷史上人類(lèi)探索圓的面積的方法不同,但不同中蘊(yùn)藏著相同——都希望“化曲為直”,即把圓這個(gè)曲邊圖形轉(zhuǎn)化為直邊圖形;而且在解決問(wèn)題的具體過(guò)程中,每種方法都不可避免地涉及“無(wú)限接近”——這也是歷史上討論最為激烈的焦點(diǎn)問(wèn)題。
因此,《圓的面積》一課教學(xué),可結(jié)合史料,依循人類(lèi)探索圓的面積的發(fā)展過(guò)程,以學(xué)生已有的經(jīng)驗(yàn)為依托(如求不規(guī)則圖形面積的“數(shù)方格”法、求取面積公式的“轉(zhuǎn)化”策略等),引領(lǐng)學(xué)生“以方測(cè)圓”——將圓的面積與正方形的面積建立聯(lián)系,給圓的面積確定一個(gè)范圍;“求精入微”——思考并想象,當(dāng)用來(lái)做單位面積的方格變得越來(lái)越小,直至無(wú)窮小時(shí),就可以準(zhǔn)確地“數(shù)”出圓的面積了;“化曲為直”——采用“切西瓜”的思路探尋圓的面積計(jì)算公式。這樣的過(guò)程中,學(xué)生充分經(jīng)歷猜想、操作、驗(yàn)證、討論和歸納等,在層層深入的活動(dòng)中體會(huì)“轉(zhuǎn)化”和“極限”思想。
二、教學(xué)過(guò)程
(一)在畫(huà)圓中喚醒已有經(jīng)驗(yàn)
師同學(xué)們,你們會(huì)畫(huà)圓嗎?老師給大家準(zhǔn)備的學(xué)習(xí)單上有個(gè)方格圖,請(qǐng)拿出圓規(guī)在上面畫(huà)一個(gè)圓。
(學(xué)生在學(xué)習(xí)單上畫(huà)圓。)
師誰(shuí)能用學(xué)過(guò)的知識(shí)介紹一下你畫(huà)的圓。
生我畫(huà)的是半徑3 cm的圓。
生我畫(huà)的是直徑4 cm的圓。
生我畫(huà)的是周長(zhǎng)25.12 cm的圓。
師通過(guò)大家的介紹,可以看出同學(xué)們從不同方面對(duì)圓有了一定的了解。根據(jù)以前學(xué)習(xí)平面圖形的經(jīng)驗(yàn),你們還對(duì)圓的什么知識(shí)感興趣?
生圓的面積。
師(板書(shū)課題:圓的面積)今天我們就來(lái)學(xué)習(xí)圓的面積。請(qǐng)同學(xué)們猜一猜,圓的面積大小可能跟什么有關(guān)?
生半徑。
生直徑。
生周長(zhǎng)。
[說(shuō)明:通過(guò)在方格紙上畫(huà)圓以及對(duì)圓的自主介紹,喚醒學(xué)生已有的經(jīng)驗(yàn),促其提出問(wèn)題,引發(fā)思考,并自然地將圓的面積與半徑、直徑甚至周長(zhǎng)建立聯(lián)系,為后續(xù)教學(xué)新知做好準(zhǔn)備。]
(二)了解古埃及“以方測(cè)圓”的思路
師圓的面積計(jì)算這個(gè)問(wèn)題,其實(shí)是古希臘三大幾何難題之一,古代人很早就開(kāi)始思考了。(播放視頻,畫(huà)面定格于圖1)古埃及人對(duì)于圓面積的探究,是借助于其與正方形面積的關(guān)系來(lái)進(jìn)行的。參考古埃及人的思路,大膽猜測(cè)一下,與一個(gè)圓有著密切聯(lián)系的正方形在哪兒?
生以圓的半徑為邊長(zhǎng)的正方形。
生以圓的直徑為邊長(zhǎng)的正方形。
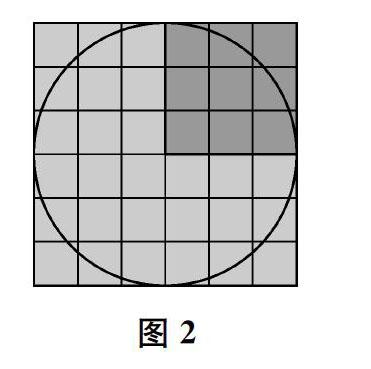
師(出示圖2)同學(xué)們的感覺(jué)很敏銳!深入思考下去,估一估,圓的面積和這兩個(gè)正方形的面積相比怎么樣?
生圓的面積比小正方形面積的2倍大一些。
師你是怎么想的?
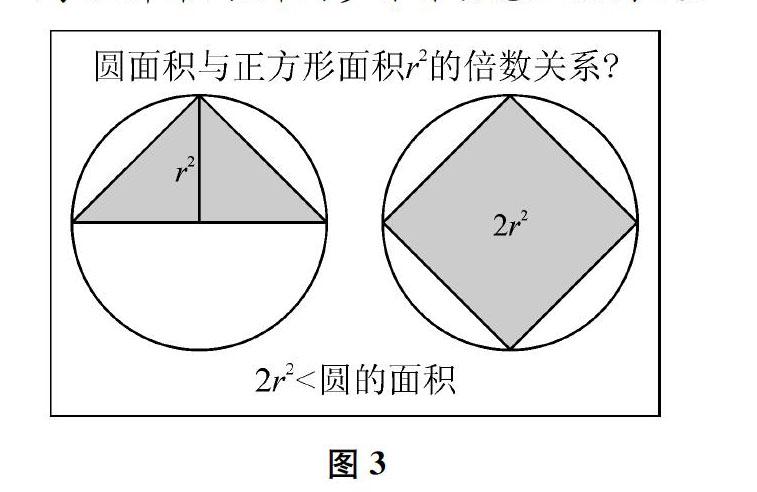
(學(xué)生解釋?zhuān)處熗秸n件動(dòng)態(tài)呈現(xiàn)圖3。)
生圓的面積比大正方形的面積小一些。
生大正方形面積是小正方形面積的4倍,說(shuō)明圓的面積比r2的4倍小一些。
(學(xué)生解釋?zhuān)處熗秸n件呈現(xiàn)圖4。)
[說(shuō)明:介紹古埃及人探究圓的面積的史料,將圓的面積與正方形的面積建立關(guān)聯(lián),引導(dǎo)學(xué)生利用方格圖中與圓的半徑和直徑關(guān)系最密切的2個(gè)正方形(以半徑為邊長(zhǎng)和以直徑為邊長(zhǎng)),估計(jì)出圓的面積的大致范圍:2r2<圓的面積 (三)化用古埃及“數(shù)谷粒”的方法“數(shù)圓” 師同學(xué)們對(duì)圓面積的大小確定了一個(gè)合理的范圍。當(dāng)然,僅有范圍還不夠,得想辦法把它們確切的倍數(shù)關(guān)系弄清楚。想一想,在方格圖中計(jì)算不規(guī)則圖形的面積,有什么經(jīng)驗(yàn)可以借用?
生可以用數(shù)方格的方法。
師好,我們就用數(shù)方格的方法來(lái)研究圓的面積到底是r2的幾倍。先把正方形的面積,也就是半徑的平方數(shù)出來(lái),是多少?
生9平方厘米。
師數(shù)圓的面積有什么好的建議嗎?
生只要數(shù)出四分之一圓的面積,然后乘4就可以了。四分之一圓大約是7.5格,圓的面積大約是30平方厘米。
師拿出計(jì)算器算一下,圓的面積大約是r2的幾倍?
生保留一位小數(shù),大約是3.3倍。
師同學(xué)們,為了使我們的實(shí)驗(yàn)數(shù)據(jù)更有說(shuō)服力,請(qǐng)大家拿出自己上課開(kāi)始時(shí)畫(huà)的圓,數(shù)出它的面積,算算面積是r2的幾倍,把結(jié)果記錄下來(lái),等待匯報(bào)。
(學(xué)生活動(dòng)后匯報(bào)數(shù)據(jù),匯總得到表1。)
表1正方形面積與圓面積的倍數(shù)關(guān)系
正方形面積
(r2)圓面積圓面積大約是正方形面積的
幾倍(精確到十分位)9303.316523.225783.1361123.1師請(qǐng)同學(xué)們仔細(xì)觀察表格,你有什么發(fā)現(xiàn)?
生圓的面積都是r2的3倍多一些。
師這就比剛才估測(cè)的范圍更精確一些了。我們把數(shù)方格的方法和古埃及人數(shù)谷粒的方法聯(lián)系起來(lái)看看。(播放視頻,畫(huà)面定格于圖5)看到3.14倍,大家就想到了什么?
生π倍。
師我們用實(shí)驗(yàn)的方法,通過(guò)大量的實(shí)驗(yàn)數(shù)據(jù)發(fā)現(xiàn),圓的面積是r2的π倍。
[說(shuō)明:數(shù)是度量的一種基本策略。這種策略指向了度量的數(shù)學(xué)本質(zhì),也有利于學(xué)生實(shí)現(xiàn)經(jīng)驗(yàn)的遷移。首先,引導(dǎo)學(xué)生利用研究不規(guī)則圖形面積的“數(shù)方格”經(jīng)驗(yàn),將自己所畫(huà)圓的面積數(shù)出來(lái),并將其與r2的倍數(shù)關(guān)系算出來(lái)。通過(guò)不同的數(shù)據(jù)對(duì)比,進(jìn)一步確定:圓的面積大約是r2的3倍多一些。結(jié)合史料介紹,用均勻分布的小格子代替谷粒,當(dāng)小格子足夠多時(shí),數(shù)方格得到的圓的面積大約是r2的3.14倍。這個(gè)環(huán)節(jié),將學(xué)生已有學(xué)習(xí)經(jīng)驗(yàn)與史料中古埃及人的探索方法相結(jié)合,通過(guò)數(shù)、算的過(guò)程將圓的面積與r2之間的倍數(shù)關(guān)系進(jìn)一步精確化。特別地,引發(fā)學(xué)生思考并想象,當(dāng)用來(lái)做單位面積的方格變得越來(lái)越小,直至無(wú)窮小時(shí),就可以準(zhǔn)確地測(cè)量出圓的面積了。借助課件,幫助學(xué)生經(jīng)歷直覺(jué)的“極限”過(guò)程,初步理解“極限”。]
(四)運(yùn)用古印度的“切西瓜”法“化曲為直”
師在數(shù)學(xué)研究中,實(shí)驗(yàn)數(shù)據(jù)確實(shí)可以說(shuō)明問(wèn)題。不過(guò),大家都知道,最嚴(yán)密、最有說(shuō)服力的方法還是——推理。同學(xué)們,以前我們?cè)谘芯恳粋€(gè)新的圖形的面積時(shí),是怎樣推導(dǎo)的?
生把新圖形用剪拼的方式轉(zhuǎn)化成學(xué)過(guò)的圖形,化未知為已知,利用新舊兩個(gè)圖形間的關(guān)系進(jìn)行推導(dǎo)。
師(出示圖6)那今天我們學(xué)習(xí)的圓,能轉(zhuǎn)化成我們學(xué)過(guò)的圖形來(lái)研究嗎?
(學(xué)生交流。)
師大家提出了一些方法。現(xiàn)在來(lái)看看古印度數(shù)學(xué)家的思路。(播放視頻,畫(huà)面定格于圖7)是不是跟我們剛才有的同學(xué)的思路相同?我們下面來(lái)試一試這種方法。老師給各組同學(xué)準(zhǔn)備了不同的學(xué)具,請(qǐng)大家沿著圓的半徑剪開(kāi),看能不能拼成熟悉的平面圖形。
(學(xué)生分組剪接,并貼到黑板上。)
師比較一下大家剪拼出來(lái)的圖,有什么發(fā)現(xiàn)?
生隨著份數(shù)的增加,拼出的圖形越來(lái)越接近平行四邊形。
師同學(xué)們,設(shè)想一下:如果平均分的份數(shù)更多,分成64份、128份、256份……這個(gè)圖形會(huì)怎么樣?
生應(yīng)該會(huì)完全接近平行四邊形。
生會(huì)完全接近長(zhǎng)方形。
師德國(guó)天文學(xué)家開(kāi)普勒也仿照“切西瓜”的方法,大膽地設(shè)想把圓分割成無(wú)窮多個(gè)小扇形。開(kāi)普勒斷言:無(wú)窮小的扇形可以看作三角形,最終拼出來(lái)的圖形就是長(zhǎng)方形。我們可以借助電腦來(lái)模擬這樣的過(guò)程。(用“幾何畫(huà)板”軟件演示圓平均分成64份、128份、256份、512份、1 028份……的情況)你們有什么感受?
生把圓平均分成無(wú)數(shù)份的時(shí)候肯定是拼成長(zhǎng)方形了。
師比較一下,圓與拼成的長(zhǎng)方形存在哪些關(guān)系?能不能根據(jù)長(zhǎng)方形的面積計(jì)算方法推導(dǎo)出圓的面積公式?
生長(zhǎng)方形的面積和圓的面積相等;長(zhǎng)方形的長(zhǎng)相當(dāng)于圓的周長(zhǎng)的一半c2,它的寬相當(dāng)于圓的半徑(r),長(zhǎng)方形的面積等于長(zhǎng)乘寬,所以圓的面積可以用圓周長(zhǎng)的一半乘半徑。那么,圓的面積公式就是S=πr×r=πr2。
(教師同步板書(shū)推導(dǎo)過(guò)程。)
師推理的結(jié)果和剛才由實(shí)驗(yàn)數(shù)據(jù)得到的結(jié)果一致:圓的面積是r2的——π倍。這樣我們就十分肯定地得出了圓面積的計(jì)算方法。
[說(shuō)明:“化曲為直”是全課的中心環(huán)節(jié)。通過(guò)豐富的活動(dòng),一方面,使學(xué)生體會(huì)圓的面積與r2的倍數(shù)關(guān)系,用“數(shù)方格”法得出結(jié)論后,更要以推理的方式加以驗(yàn)證,亦即數(shù)學(xué)結(jié)論的得出過(guò)程應(yīng)該是從猜想到實(shí)驗(yàn)驗(yàn)證再到推理證明的科學(xué)過(guò)程,將合情推理與演繹推理相結(jié)合,培養(yǎng)學(xué)生嚴(yán)謹(jǐn)?shù)目茖W(xué)態(tài)度和理性精神;另一方面,則是將學(xué)生的“轉(zhuǎn)化”經(jīng)驗(yàn)遷移到新知中來(lái)。結(jié)合史料中古人的探索,組織學(xué)生在親自動(dòng)手操作,進(jìn)一步積累經(jīng)驗(yàn)的基礎(chǔ)上,通過(guò)想象活動(dòng)深刻感受“極限”思想。整個(gè)過(guò)程中,努力將學(xué)生的已有經(jīng)驗(yàn)與人類(lèi)的探索過(guò)程無(wú)縫對(duì)接,使他們真正經(jīng)歷“再發(fā)現(xiàn)”“再創(chuàng)造”過(guò)程。]
(五)回顧梳理歷史研究軌跡
師同學(xué)們,現(xiàn)在你能算出開(kāi)始的時(shí)候自己所畫(huà)的圓的面積了嗎?動(dòng)手算一算。
(學(xué)生運(yùn)用公式計(jì)算后交流。)
師大家把算出來(lái)的面積與之前數(shù)方格得到的面積比一比,有什么感受?
生根據(jù)公式計(jì)算出的數(shù)據(jù)比較精確,數(shù)方格得出的數(shù)據(jù)有誤差。
師回顧一下今天的研究過(guò)程,我們是怎么得出結(jié)論的?
生先是猜測(cè)圓的面積與半徑的平方有倍數(shù)關(guān)系;然后估一估,發(fā)現(xiàn)圓的面積是半徑平方的2倍—4倍;接著數(shù)一數(shù),通過(guò)實(shí)驗(yàn)數(shù)據(jù)發(fā)現(xiàn)圓的面積是半徑平方的3.14倍;最后通過(guò)剪拼,將圓轉(zhuǎn)化成長(zhǎng)方形,成功推導(dǎo)出了圓面積的計(jì)算公式,確定了圓的面積是半徑平方的π倍。
師總結(jié)得很好!我們借鑒了古人的智慧,結(jié)合了自己學(xué)習(xí)平面圖形面積的經(jīng)驗(yàn),沿著歷史的足跡,經(jīng)歷了一個(gè)數(shù)學(xué)結(jié)論得出的完整過(guò)程。剛剛有同學(xué)問(wèn)我:圓被平均分成若干份之后,那些小扇形還能拼成其他的平面圖形嗎?課后大家不妨去剪一剪、拼一拼、想一想、算一算,相信你一定會(huì)有更大的收獲!
[說(shuō)明:得出圓的面積計(jì)算公式后,讓學(xué)生準(zhǔn)確計(jì)算出課始自己所畫(huà)圓的面積,并與之前數(shù)方格得到的面積數(shù)據(jù)進(jìn)行對(duì)比,體會(huì)數(shù)學(xué)的精確性及應(yīng)用性。引導(dǎo)學(xué)生回顧整節(jié)課的研究過(guò)程,讓學(xué)生體會(huì)到自己在課堂上經(jīng)歷了人類(lèi)千年的探索過(guò)程,幫助學(xué)生在感受數(shù)學(xué)文化的同時(shí),體驗(yàn)數(shù)學(xué)探索的“逐步精確化”。最后,引發(fā)學(xué)生對(duì)圓的面積公式其他推導(dǎo)方法的深入思考,為今后的學(xué)習(xí)研究奠定扎實(shí)的基礎(chǔ)。]
參考文獻(xiàn):
[1] 鄭瑋,鄭毓信.HPM與數(shù)學(xué)教學(xué)中的“再創(chuàng)造” [J].數(shù)學(xué)教育學(xué)報(bào),2013(3).
[2] 王曉軍,汪曉勤. HPM視角下的“圖形旋轉(zhuǎn)”問(wèn)題探究[J].數(shù)學(xué)通報(bào),2012(5).
[3] 陳金飛.獨(dú)到的,才是不可替代的——HPM 視角下對(duì)“圓的面積”的思考與教學(xué)實(shí)踐[J].江蘇教育,2015(17).
[4] 弗賴(lài)登塔爾.作為教育任務(wù)的數(shù)學(xué)[M].陳昌平,唐瑞芬,等編譯.上海:上海教育出版社,1995.

