對稱三勢阱玻色—愛因斯坦凝聚體的非線性效應
舒鵬麗,王燕鋒,雒衛廷
(呂梁學院物理系,山西呂梁 033000)
自1995年首次實現堿金屬氣體原子的玻色—愛因斯坦凝聚[1]以來,原子間的非線性相互作用就成為研究者關注的內容之一。雙勢阱的BECs 體系作為研究量子非線性隧穿行為的重要模型[2],引發了很多迥異的物理現象,如能級的拓撲結構[3],非線性不穩定態的存在[4]等,特別是非線性約瑟夫振蕩和自囚禁現象[5],實驗中用BEC 的吸收譜直接觀測到這一現象[6]。隨著研究的深入,有不少工作致力于三勢阱的BECs 體系[7],使得人們對BECs 的宏觀量子隧穿效應有了更深刻的理解。對于三勢阱的BECs 體系,利用平均場近似得到的Gross-Pitaevskii 方程和經典哈密頓理論[8],來研究復空間的量子波函數和非線性的量子演化。本文從非線性薛定諤方程出發,在一定的初值條件下,研究粒子在三勢阱中出現的幾率密度隨非線性作用的演化關系。
1 物理模型
三勢阱中的BECs 在平均場近似下,可以用Gross-Pitaevskii 方程[4,8]來描述,其中GP 方程的波函數ψ(r,t)是3個勢阱中波函數的疊加,表示為:
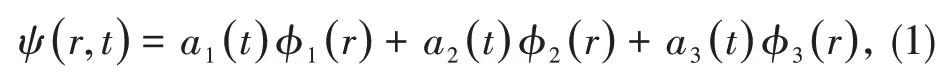
其中,φj(r)可看作第j(j=1,2,3)個能級的基態波函數,aj(t)=是概率幅,滿足
經代換,三勢阱的BECs 體系可用非線性Schr?dinger方程[9]描述:

假設第二個勢阱的零點能為0,γ和-γ是第一個勢阱和第三個勢阱的零點能,c是原子之間的相互作用強度,在討論中,設c>0,即原子之間相互排斥,v是三勢阱間的耦合常數。式(3)多出了原子相互作用導致的非線性項這時候Schr?dinger 方程式(2)不能解析求解,只能從數值上研究[10]非線性項所帶來的物理效應。
2 對稱三勢阱,即γ=0
2.1 幾率密度在強弱非線性作用下的變化
從圖1 可以看出,在弱相互作用c=0.4 下,粒子在3 個勢阱間出現的幾率呈現Josephson 振蕩。(a)初始時,粒子都放在第一個勢阱中,隨著時間的演化,粒子可通過第二個勢阱隧穿到第三個勢阱,然后再隧穿回來;(b)初始時,粒子都放在中間勢阱中,粒子可隧穿到兩邊的勢阱,且左右勢阱呈現相同的振蕩周期;(c)初始時,粒子均勻分布在相鄰的兩個勢阱中,勢阱中的粒子都可隧穿到第三個勢阱中,但是中間勢阱的隧穿概率明顯小于左邊勢阱;(d)初始時,粒子均勻分布在不相鄰的兩個勢阱中,兩邊勢阱中的粒子可隧穿到中間勢阱中,且左右勢阱具有相同的振蕩周期。另外圖1(b)和(d)顯示,粒子相對勢阱對稱放置時,振蕩具有相同的周期。
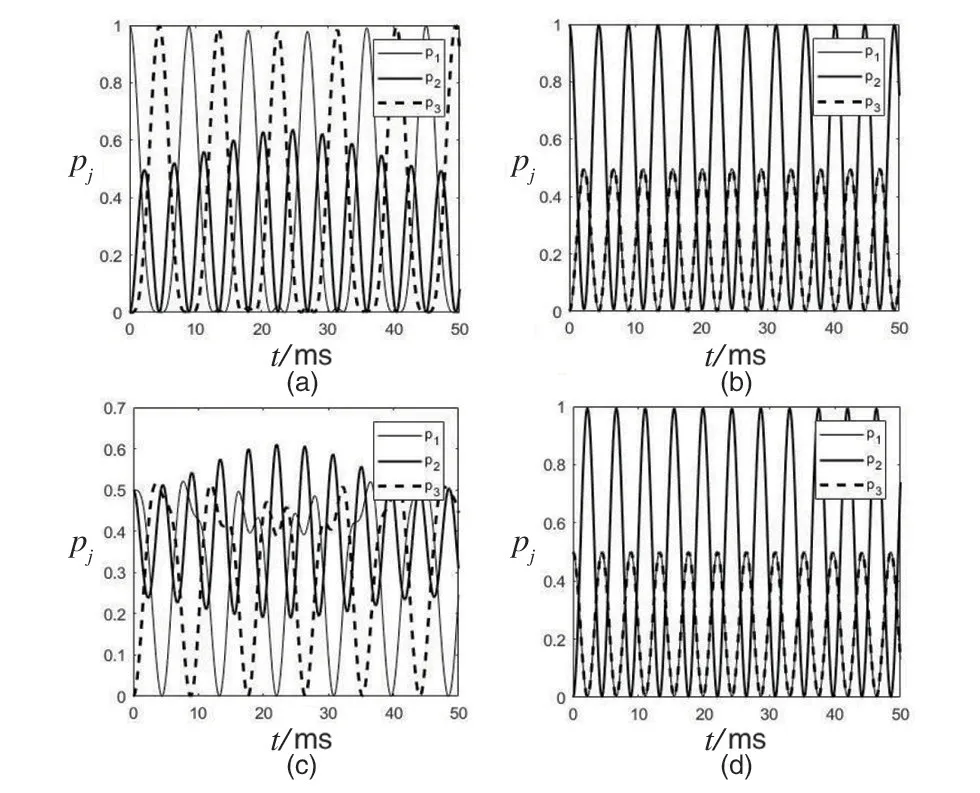
圖1 幾率密度pj在弱非線性作用下隨時間的演化
圖2(a)和(b)為強相互作用c=5,(c)和(d)為強相互作用c=10,粒子在不同的初值條件下,都表現出自囚禁行為,這和對稱雙勢阱中的BECs 在強非線性作用的情況正好吻合[11]。
2.2 平均幾率密度隨非線性作用強度的變化
為更好地理解粒子在對稱三勢阱出現的幾率密度隨非線性作用的變化,引入平均幾率密度

圖3 平均幾率密度隨非線性相互作用c的演化
(a)初始時所有的粒子放在第一個勢阱中,當0 (b)初始時所有的粒子放在第二個勢阱中,當非線性作用小于臨界值時,粒子從第二個勢阱隧穿到左右兩個勢阱中,做周期性振蕩,第一個勢阱和第三個勢阱中的粒子具有相同的振蕩行為,隨著非線性作用的增大,粒子的隧穿行為逐漸減弱,發生自囚禁現象。 (c)初始時在第一個勢阱和第二個勢阱中各放入相等數量的粒子,粒子在非線性作用0 (d)初始時在第一個勢阱和第三個勢阱中各放入相等數量的粒子,第一個勢阱和第三個勢阱中的粒子具有相同的振蕩行為,這兩個勢阱中的粒子隧穿到中間勢阱中,振蕩隨著非線性作用的增大逐漸減弱,當c>7.8時,粒子被束縛在各自的勢阱中。 圖3(b)和(d)可以看出,當粒子相對勢阱對稱放置時,第一個勢阱和第三個勢阱的粒子的振蕩行為相同,約瑟夫振蕩和自囚禁現象隨非線性作用的增大變化明顯。當粒子相對勢阱中不對稱放置時,圖3(a)和(c),粒子的振蕩隨非線性作用的變化出現混沌,說明對稱三勢阱中粒子的行為不僅受到非線性作用的影響,同時也受到不對稱初始值的影響。 圖3(a)和(c)發現,當粒子在勢阱中不對稱放置時,粒子的振蕩隨非線性作用的變化出現混沌。對方程(2)進行正則變換[4],對稱三勢阱BECs 構成的3能級量子系統相應的正則方程為 從(4)~(7)式可以判斷p1、p2、p3、θ1、θ2,也可通過正則方程求得,并且p1、p2、p3的值受初始相對相位θ1、θ2的影響。如圖4,選取初值(a)(p1=0.7,p2=0.3,p3=0,θ1=0,θ2=π/2);(b)(p1=0.7,p2=0.3,p3=0,θ1=0,θ2=π),研究平均幾率密度隨非線性作用的變化關系。圖4(a)中粒子振蕩出現明顯的混沌區域,改變初始相對相位的取值,如圖4(b),粒子的混沌行為被減弱,振蕩較平穩地由混沌轉為自囚禁,可以看出相對相位可以控制混沌的產生和轉變。 圖4 平均幾率密度在改變初始相位下的演化 利用平均場近似得到三勢阱BECs 的非線性薛定諤方程,采用數值求解的方法,模擬在不同的非線性相互作用c下,粒子出現的幾率,可得到BECs 相應的非線性隧穿行為—約瑟夫振蕩和自囚禁,而且在一定的非線性作用范圍內下,粒子出現不規則振蕩,即混沌現象,如改變相對相位的初始值,混沌可以平穩地轉變為自囚禁狀態,這為研究非對稱三勢阱的非線性效應提供一定的理論基礎。2.3 混沌可通過改變相位初值轉變為自囚禁
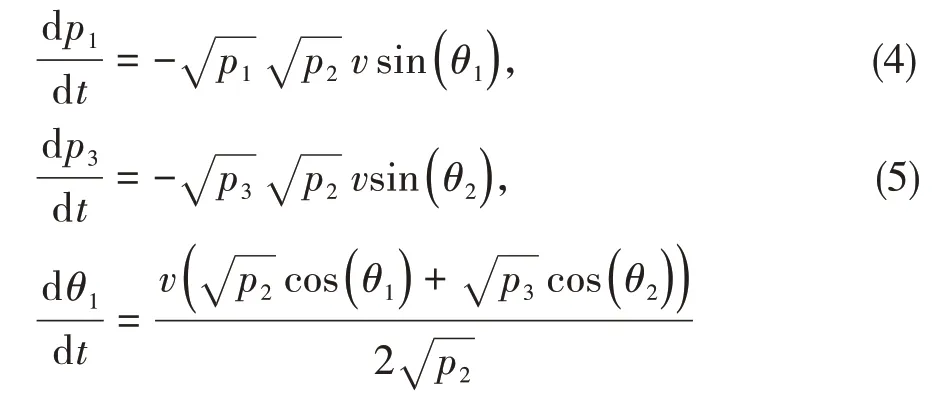

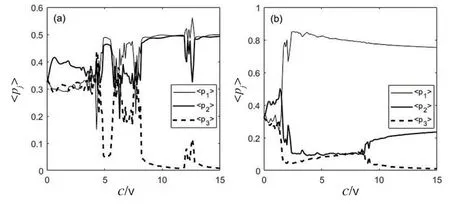
3 結語

