平穩的ARFIMA模型中參數的Whittle估計的糾偏

張秀珍，孟獻青

(山西大同大學數學與統計學院，山西大同 037009)

對時間序列而言，時域分析和頻域分析是常用的兩種分析方法。當假設模型服從高斯分布時，運用精確的時域極大似然方法可以得到的未知參數極大似然估計，這個估計具有非常好的統計性質，這是眾所周知的。然而在計算極大似然函數時，當分布維數較高時計算分布的方差矩陣的逆要花費很大精力。為了避免計算方差矩陣的逆，文獻[1]從頻域角度出發，通過傅里葉變換建立了Whittle 似然，該似然函數近似等價于精確的極大似然從而對未知參數做統計推斷更容易。自此，Whittle 似然在時間序列的統計推斷中得到廣泛應用。然而，這種估計方法與最大似然估計相比較，其弊端在于它的估計偏差比較大，因而各種糾偏方法應用而生。比如：文獻[2]通過用周期圖的期望替代Whittle 似然函數中譜密度函數構造新的偽似然以減小Whittle 估計的偏差。另外常用的糾偏方法如刀切法，通過一種重抽樣方法來實現減小估計的偏差。也就是，在給定n個樣本的情形下，通過每次選擇m個子樣本去估計未知參數，文獻[3]通過刀切法減小二階平穩模型中Whittle 估計的偏差。長記憶模型是自從水文學家Hurst 第一次發現900 個數據的自相關性表現出一種緩慢衰減的特性開始得到廣泛關注的。越來越多的研究者注意到觀測到的數據表現出這樣一種趨勢，那么識別在或空間上相距甚遠的觀測之間的這種相關性在許多不同的領域和學科中越來越被廣泛關注。通過自相關函數呈現出的以雙曲速率衰減的特性表現其長記憶性,關于長記憶過程的特征可參考專著[4-5]。從Whittle 估計出發，分別運用刀切法和文獻[2]所給出的方法以及把兩種方法結合起來，減小平穩的ARFIMA 模型中的參數的估計的偏差，通過蒙特卡洛模擬實驗驗證所給出的方法的有效性。

1 ARFIMA模型的參數估計方法

對于平穩的ARFIMA 模型下的參數估計的糾偏方法，我們從Whittle估計出發引入主要方法。

1.1 ARFIMA模型的Whittle估計

隨機過程{Xt} 被稱為平穩的ARFIMA(p,d,q)模型，若滿足

其中，{εt} 為均值為0 方差為σ2的白噪音，φ(B)=1+分別是后切算子B(BiXk=Xk-i)的p階和q階多項式并且滿足：其對應的方程沒有公共根且所有根都落在單位圓外。其自協方差函數以多項式階衰減，這里d稱為記憶參數，d>0 保證過程的平穩性，當d<1/2 時，{Xt} 是長記憶過程。

這個模型中的未知參數向量β=(φ1,…,φp,d,θ1,…,θq,σ2)∈Ξm，其中m=p+q+2 是未知參數的維數，Ξm是m維歐氏空間的一個緊子集。那么對β的離散對數Whittle似然定義為

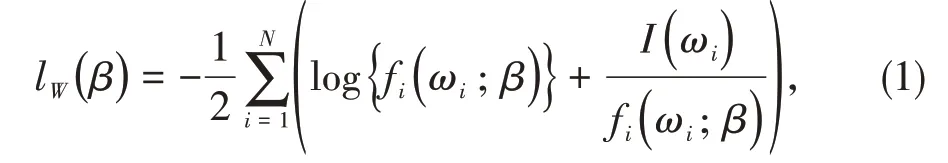
其中，ωj=2jπ/T，j=1,…,N=[(T-1)/2]([·]定義取整函數)，周期圖{I(ωj)}表達式如下：

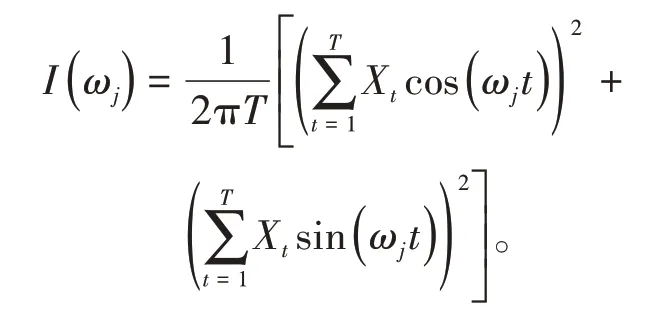
f(ω;β)是ARFIMA模型的譜函數，其表達式為

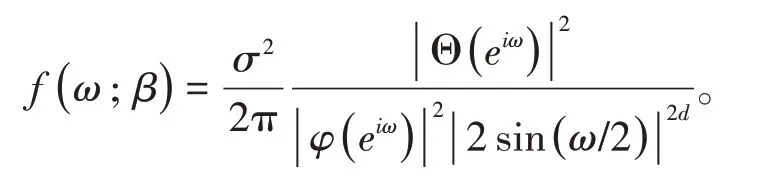
最大化Whittle似然函數求得β的Whittle估計

而實際中σ2由于其不影響模型的主要特征，例如譜函數，所以通常視σ2為冗余參數，所以事實上的參數是

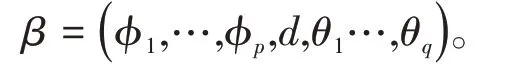
1.2 的糾偏方法

將導出幾種糾偏方法，首先從文獻[2]給出的糾偏方法出發，通過替換Whittle 似然中的譜函數為周期圖的期望，定義一種新的偽似然為

而β隱含在自協方差τk,k=0,1,…,N-1 中，i是虛單位，Re(·)表示實部函數。這就是Debiased Whittle 似然，簡稱為DW似然。在DW似然下，β的估計為

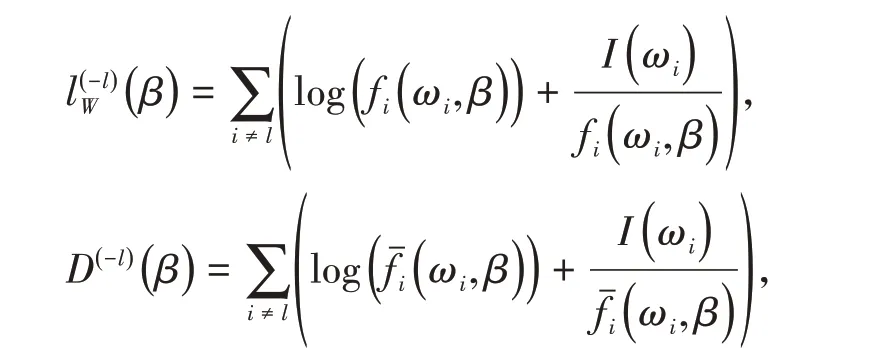
且

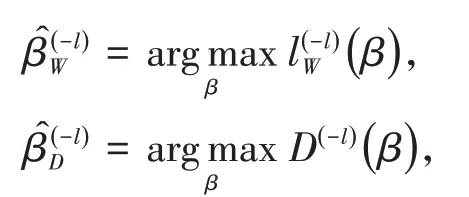
那么刀切估計分別為

2 數值模擬

在ARFIM(0，d，0)模型下，運用所給出的方法實現減小參數估計的偏差。設定時間序列的長度T=200,500,1000，分別假設噪聲擾動為N(0,1)、t(5)、χ2(5)、Exp(1)，每種情形重復10000 次模擬計算估計的偏差、標準差、均方誤差以及R軟件的計算時間。表1列出了在各種情形下的四種估計的各指標。

從表1 可見，對于ARFIMA 模型，刀切法在減小偏差的同時損失了計算效率，且在樣本量相對較小時，刀切估計不穩健；在樣本量較大刀切法確實是減小了估計的偏差且與Whittle 估計相比較，均方誤差幾乎保持不變；DW 雖然保持了Whittle估計的計算效率，但估計的偏差減小不明顯。

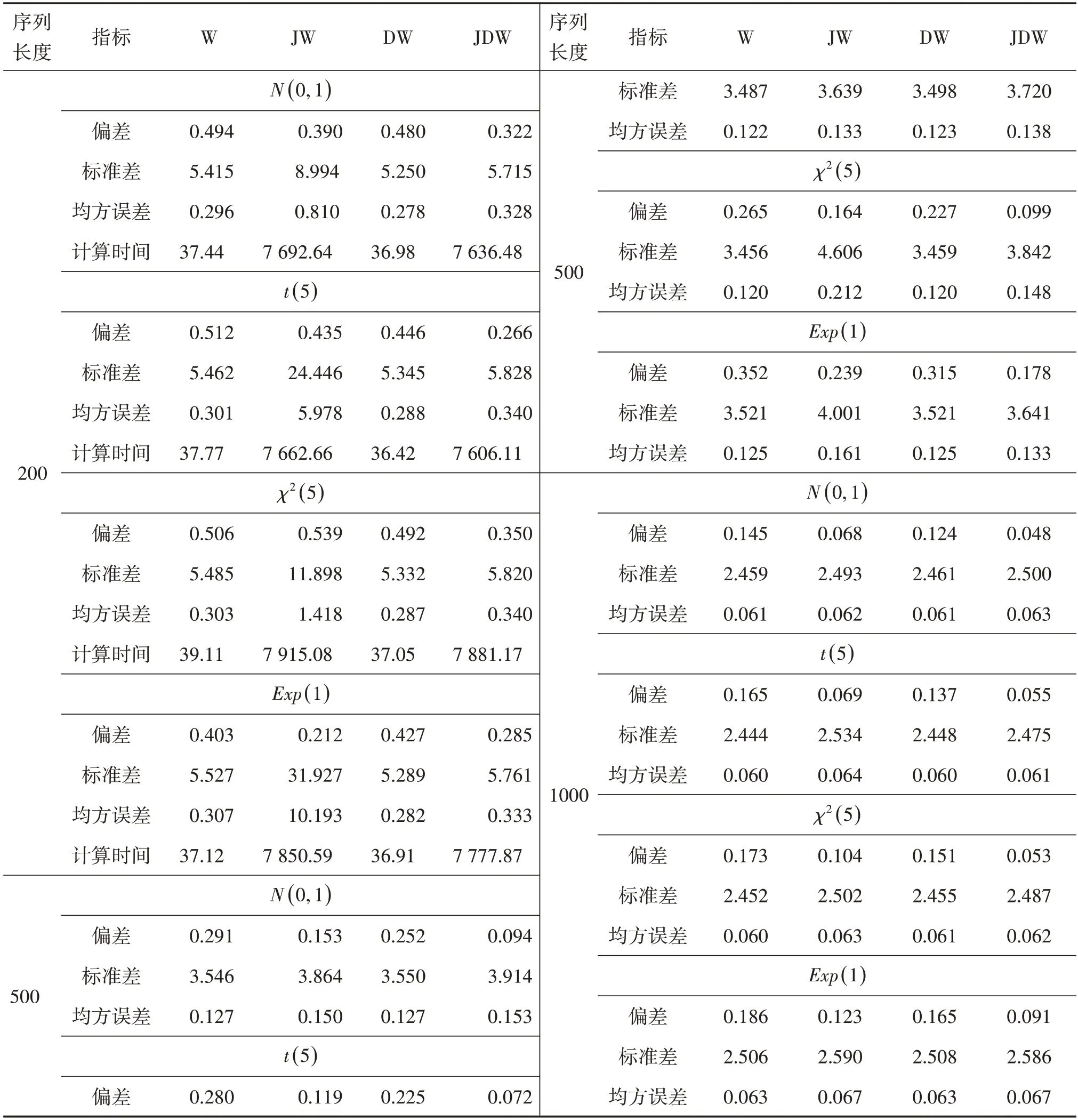
表1 ARFIMA(0,d,0)取序列長度d=0.1的估計

3 結語

考慮在ARFIM(p，d，q)模型下減小參數的Whittle估計的偏差，通過刀切法和Sykulski 等給出的方法，實現了減少參數估計偏差的目的。但我們發現刀切法在減小估計偏差的同時使得計算效率變差，而Sykulski等所給出的方法對減小ARFIMA模型的參數的Whittle 估計的偏差效果不明顯，因而尋找更優質的方法減小估計的方法仍是一項迫在眉睫的工作。Sykulski 等強調Whittle 估計的偏差是由周期圖是譜函數的有偏估計所致，所以這給出我們一種啟示，從Whittle 似然出發構造新的偽似然，從而減小Whittle估計的偏差是最根本的、最有效的途徑。